Data Structure and Algorithms (C++ Implementation) Learning Notes (7)
1. chain stack
Introduction of 1.1 Chain Stack
Chain stack is a data storage structure, which can be implemented by single linked list. The advantage of using chain stack is that it can overcome the low utilization of sequential stack space realized by array, but it needs to allocate extra pointer space for each stack element to store pointer fields.
Stack is a special linear table that can only be inserted and deleted at one end. It stores data according to the principle of "first in, last out". The first in data is pushed to the bottom of the stack, and the last data is pushed to the top of the stack. The elements in the chain stack are stored as Node, and the elements in the node Node and the pointer to the next node are stored in the node Node. Data members of a chain stack use only the pointer * top_node pointing to the top node of the stack.
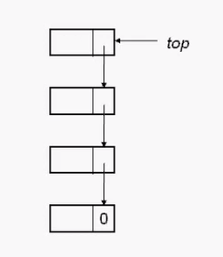
1.2 Chain Stack and Sequential Stack
The implementation of sequence stack is based on the basic data structure of array. The elements of array are stored in memory continuously, and the compiler requires us to determine the size of array at compile time, so the efficiency of memory usage is not high, so it is inevitable that the array space is used up. Overflow problem, second, after the system allocates memory to the array, these memory will not be available for other tasks; for the chain stack, the chain table is used to implement the stack, the elements in the chain table are stored in discontinuous addresses, because it is dynamic memory application, so we can start with very small memory space, in addition. Memory can also be returned to the system when an item is not used.
1.3 code implementation chain stack
1. Design of Chain Stack
#ifndef LINKEDTASCK_H
#define LINKEDSTACK_H
template<class T> class LinkedStack;
template<class T>
class ChainNode
{
friend class LinkedStack<T>;
private:
//The data in the node is stored in the data for the node to which the new node refers.
ChainNode(const T& theData, ChainNode *n = 0)
:data(theData),link(n) {}
T data;
ChainNode<T> *link;
};
template<class T>
class LinkedStack
{
public:
LinkedStack() :top(0) {}
~LinkedStack() { MakeEmpty(); }
bool IsEmpty() const;
T& Top() const;
void Push(const T& e);
void Pop();
void MakeEmpty();
private:
ChainNode<T> *top;
};
template<class T>
bool LinkedStack<T> ::IsEmpty() const
{
return top == 0;
}
template <class T>
void LinkedStack<T>::Push(const T&e)
{
top = new ChainNode<T>(e, top);
}
template <class T>
T& LinkedStack<T>::Top() const
{
if (this->IsEmpty())
throw "Stack is empty.";
return top->data;
}
template<class T>
void LinkedStack<T>::Pop()
{
if (this->IsEmpty())
throw "Stack is empty. Cannot delete.";
ChainNode<T>* delNode = top;
top = top->link;
delete delNode;
}
template <class T>
void LinkedStack<T>::MakeEmpty()
{
while (!IsEmpty())
Pop();
}
#endif
2. Test Chain Stack
#include<iostream>
#include "linkedstack.h"
//For testing
using namespace std;
int main()
{
LinkedStack<int> s;
s.Push(10);
cout << s.Top() << endl;
s.Push(20);
cout << s.Top() << endl;
s.Push(30);
cout << s.Top() << endl;
//s.Pop();
//cout << s.Top() << endl;
return 0;
}2. Chain queue
2.1 Chain Queue Brief Introduction
Queue is a special linear table, which only allows deletion at the front of the table, but insertion at the back of the table. Like stack, queue is a restricted linear table. The end of the insertion operation is called the end of the queue, and the end of the deletion operation is called the head of the queue.
In the process of queue formation, the principle of linear linked list can be used to generate a queue. Queues based on linked lists are inefficient to create and delete nodes dynamically, but they can grow dynamically. FIFO(first in first out) is used in the queue. New elements (elements waiting to enter the queue) are always inserted at the end of the list, and read from the head of the list. Read one element at a time and release one element at a time. So-called dynamic creation, dynamic release. Therefore, there is no spillover problem. Because the linked list is indirectly formed by the structure, it is also convenient to traverse.
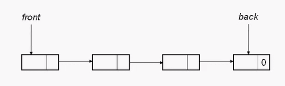
1. Entry operation
Add the element at the end of the queue, first point the next of the element at the end of the queue to the added element, and then point the pointer at the new end of the queue again.
2. Out-of-line operation
Head node points to the end of the team, the operation is to kill the end of the team, first point to the new end of the team (that is, the successor of the old end of the team), and then release the old end of the team. If there is only one element in the list except the header node, it is necessary to point the rear to the header node.
2. Code implementation of chain queue
1. Implementing chain queue
#ifndef QUEUELI_H
#define QUEUELI_H
template<class T>
class Queue
{
public:
Queue();
~Queue();
bool isEmpty() const;
const T& getFront() const;
void enqueue(const T& x);
T dequeue();
void MakeEmpty();
private:
struct ListNode
{
T element;
ListNode *next;
ListNode(const T& theElement, ListNode *n=0)
:element(theElement),next(n) {}
};
ListNode *front;
ListNode *back;
};
template<class T>
const T& Queue<T>::getFront() const
{
if (isEmpty())
throw"Queue is empty.";
return front->element;
}
template<class T>
Queue<T>::Queue()
{
front = back = 0;
}
template<class T>
Queue<T>::~Queue()
{
MakeEmpty();
}
template<class T>
bool Queue<T> ::isEmpty() const
{
return front == 0;
}
template <class T>
void Queue<T>::enqueue(const T& x)
{
if (isEmpty())
back = front = new ListNode(x);
else
back = back->next = new ListNode(x);
}
template<class T>
T Queue<T> ::dequeue()
{
T frontItem = getFront();
ListNode *old = front;
front = front->next;
delete old;
return frontItem;
}
template <class T>
void Queue<T>::MakeEmpty()
{
while (!isEmpty())
dequeue();
}
#endif
2. Test chain queue
#include<iostream>
#include"QueueLi.h"
using namespace std;
int main()
{
Queue<int> myQ;
myQ.enqueue(10);
myQ.enqueue(20);
myQ.enqueue(20);
cout << myQ.getFront() << endl;
myQ.dequeue();
cout << myQ.dequeue() << endl;
cout << myQ.dequeue() << endl;
for (int j = 0; j < 8; j++)
{
for (int i = 0; i < 8; i++)
myQ.enqueue(i);
while (!myQ.isEmpty())
cout << myQ.dequeue() << endl;
}
}Reference video:
https://www.bilibili.com/video/av31763085/?p=19
https://www.bilibili.com/video/av31763085/?p=20