Chapter I basic algorithm (I)

1, Content overview

Master the main ideas and have a deep understanding

Understand and memorize the code template (master the idea)

Template topic exercise

Understanding + memory

1. Sorting:

• Quick row
• Merge sort

2. Two points

• Integer dichotomy
• Floating point binary

2, Quick sort

The main idea of quick sort is based on divide and conquer. The first step is to determine the dividing point and focus on adjusting the range.

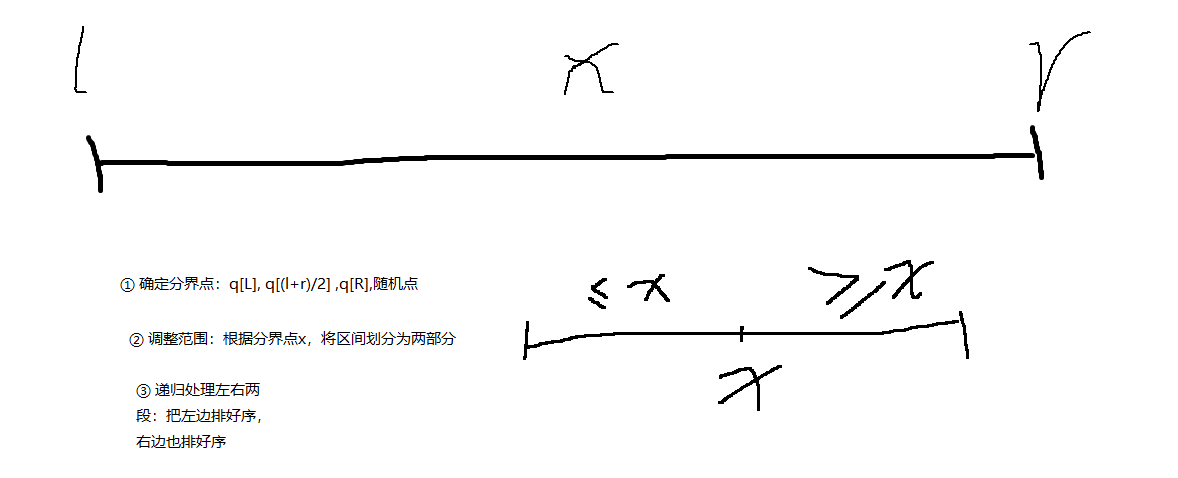
1. Double pointer thought (a little more beautiful than the violent practice above)

(1) Thought:

• There is no need to open up additional space
• There are two pointers i and j, which are at the leftmost and rightmost ends respectively
• Then i and j go to the middle
• i go to the middle until i encounter the first number greater than x, and then stop (because those greater than x should be placed on the right half) [i continue to go down when i encounter a number less than x]
• j go to the middle until it meets the first number less than x, and then stop (the number less than x is placed on the left half)
• At this time, exchange the number referred to by i with the number referred to by j, then the new number referred to by i is the number less than x, and the new number referred to by j is the number greater than x.
• Then repeat this process, i, j go to the middle;
• Until i and j meet, the interval can be divided into two [the left is less than X and the right is greater than x]
• It will be found that at any time, the number on the left of i is less than x, and the number on the right of j is greater than x
• When two pointers meet or pass through, the number on the left of the two pointers is greater than or equal to x, and the number on the right is greater than or equal to x, which is perfectly divided into two intervals
• [once x returns, divide the interval, and recurse the left and right intervals until all x returns]

(2) Quick release template: ACWING 785 Quick sort

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 10;
int n;
int q[N];
void quick_sort(int q[], int l, int r)
{
	if (l >= r) return ; // If the array has no or only one number, there is no need to sort
	
	//Set two pointers and the dividing point x 
	int x = q[l], i = l - 1, j = r + 1; //Here, we set the two pointers outside the array, so that we can ignore them and directly let both go inside
	
	//Start cycle
	while (i < j)
	{
		//You can only go on without two pointers
		do ++i; while (q[i] < x); //When Q [i] < x, keep going
		do --j; while (q[j] > x); //When Q [J] > x, continue to go down until the j pointer points to a number < = x, indicating that it should be placed on the left
		
		//Judge that the two pointers I and J can be exchanged without touching
		if (i < j) swap(q[i], q[j]); 
	} 
	//After the end of a cycle, the dividing point x returns, and then continues to recurse on the left and right sides respectively
	quick_sort(q, l, j);
	quick_sort(q, j + 1, r); 
}
int main ()
{
	scanf ("%d",&n); // How many numbers are entered
	for (int i = 0; i < n; ++i)
	{
		scanf ("%d",&q[i]); // Input array 
	} 
	
	// Quick sort
	quick_sort(q, 0, n - 1);//Range 0 - n-1
	for (int i = 0; i < n; ++i) printf ("%d ",q[i]);
	printf ("\n");
	return 0; 
}

• quick_ Note in sort: when writing i, it's best not to use q[l], otherwise there will be boundary problems. Change it to i, as follows:

  int x = q[r];
  //perhaps
  int x = q[(l + r + 1) / 2]; // It must be rounded up. It must not be rounded up to l this boundary
  quick_sort(q, l, i - 1);
  quick_sort(q, i, r); 
  //When we use i here, we must not get the left boundary of l, otherwise it will be dead circulation
  

• For example, consider:

/* 
For example:
2
1 2
*/
- If at this time x = q[l]，then is x = 1;
- first, i Point in front of the first point 1, j Point behind the second point 2
- With do-while Both pointers will start first++Move it
- The first point is not less than x，i++，Point to the first point 1;
- The second point satisfies greater than x,And before++ After that, go forward and point to the first point 1. The two pointers meet
- here i=0，Equal to left boundary l;
- here quick_sort(q, 0, -1); // There's no number on the left. It's over
- here quick_sort(q, 0, 1); // Next time it will be [0, 1]
- It will continue to loop and recurse infinitely
- Boundary problem
- The same applies j Don't use it when you need it r(Left not left, right pointer not right boundary)

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 10;
int n;
int q[N];

void quick_sort(int q[], int l, int r)
{
   if (l >= r) return ;
   int x = q[r];
   int i = l - 1;
   int j = r + 1;
   while (i < j)
   {
       do ++i; while (q[i] < x);
       do --j; while (q[j] > x);
       if (i < j) swap(q[i], q[j]);
   }
   quick_sort(q, l, i - 1);
   quick_sort(q, i, r);
}

int main ()
{
   scanf ("%d", &n);
   for (int i = 0; i < n; ++i)
   {
       scanf ("%d", &q[i]);
   }
   quick_sort(q, 0, n - 1);
   for (int i = 0; i < n; ++i)
   {
       printf ("%d ",q[i]);
   }
   printf ("\n");
   return 0;
}

• On the latest ACwing 785, the data is updated so that the dividing point x = q[(l + r + 1) / 2]; You can pass this question

3, Merge sort

Based on thought: divide and conquer

• Fast row is divided first, and then recursion on the left and right sides;
• Merging is to recurse the left and right sides first, and then do some other operations

1. The idea of merging and sorting:

• Step 1: determine the dividing point: mid = (l + r) / 2;
• Step 2: recursively sort left and right sides;
• Step 3: after the left and right sides are ordered, merge again - combine two ordered numbers into one;

(1) How to merge? ★

• Double pointers, respectively pointing to two arrays to be merged;

• Then, compare the numbers pointed to by the two pointers, put the smaller one in the final result array, and then move the pointer pointing to the smaller one back, then compare and repeat the process;

• Keep comparing, and the pointer keeps moving back; If one of the pointers points to the end (none) and the other pointer points to an array that is left, put all of them into the result array (indicating that these are large numbers)

• Stability means that if the values of two numbers in the original sequence are the same, the sorting is stable if the relative position does not change after sorting

• Merge sort is stable, and quick sort is generally unstable;

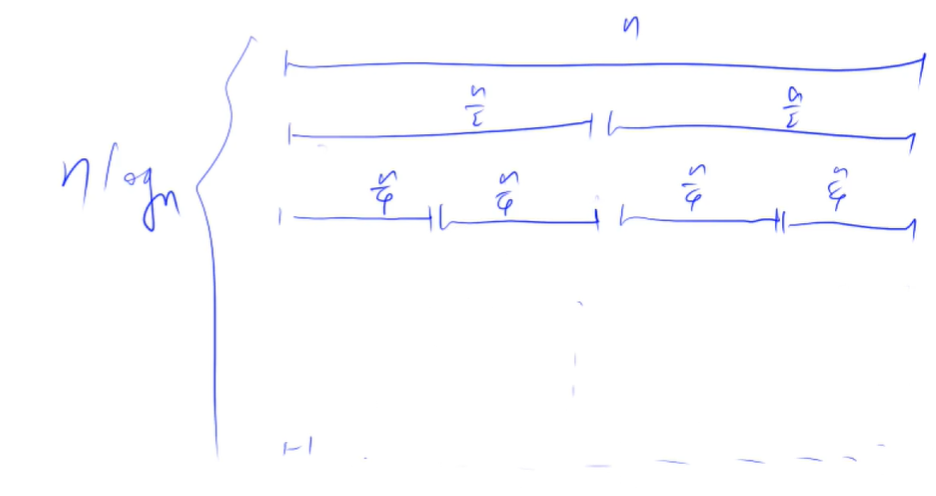
• Average time complexity of fast scheduling: O(nlogn);

• Merge sort: O(nlogn); n / log2n times 2 equals 1

• 

(2)ACwing 787. Merge sort

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 10;

int n;
int q[N]; //data 
int temp[N]; //Store temporary data array 

void merge_sort(int q[], int l, int r)
{
	if (l >= r) return; //If there is only one data or no data in the array, the exit function is returned directly
	
	//Determine the dividing point first 
	int mid = l + r >> 1; // Bit operation / 2
	
	//Recursive sort left and right
	merge_sort(q, l, mid); //Recursive sort left 
	merge_sort(q, mid + 1, r); //Recursive sort right
	
	//Merge
	int k = 0; //Number of merging
	// Two pointers 
	int i = l; 
	int j = mid + 1; 
	// Point to the left and right sides of the order, and then merge
	//Merging is the merging of ordered arrays 
	while (i <= mid && j <= r)
	{
		// If the number pointed to by the i pointer is less than that pointed to by the j pointer, insert the number pointed to by i into the temporary array, and i and k go down
		//Similarly, j k 
		if (q[i] <= q[j]) temp[k++] = q[i++];
		else temp[k++] = q[j++];	
	} 
	// When i is not finished and j is finished, put the remaining arrays in the temporary array temp 
	while (i <= mid) temp[k++] = q[i++];
	// Similarly, the right half 
	while (j <= r) temp[k++] = q[j++];
	
	//Sort out the temporary array and re assign it back to the q array 
	for (i = l, j = 0; i <= r; ++i, ++j)
	{
		q[i] = temp[j];	
	} 
} 

int main ()
{
	scanf ("%d", &n);
	for (int i = 0; i < n ; ++i)
	{
		scanf ("%d",&q[i]);
	}
	merge_sort(q, 0, n - 1);
	for (int i = 0; i < n ; ++i)
	{
		printf ("%d ",q[i]);
	}
	printf ("\n");
	return 0;
}

4, Bisection (integer bisection and floating point bisection)

1. Integer dichotomy: (back template)

Essence: it has nothing to do with monotonicity, but if there is monotonicity, there must be dichotomy. [topics that can be divided into two parts are not necessarily monotonous];

The essence of dichotomy is a boundary. Suppose we are given an interval, and then we define a property on this interval, so that this property is satisfied in the right half and unsatisfied in the left half;

The whole interval can be divided into two;

As long as this property can be found in the whole interval, the boundary point can be bisected by bisection;

(1) First case

• Suppose you want to dichotomize the red dot;
• step one: let the middle point mid = (l + r) / 2 first;
• Assuming that the property is red, first check whether the mid meets the property of red, if (check(mid));
• If the result is true, it means that the red property is satisfied. Find it in the red block (mid is in the red interval), and the answer is between [mid, r] [including mid, mid can get the boundary point]; The update method is [l, r] interval, which is updated to [mid, r] interval; [l = mid]
• If it is false, it indicates that the red property is not satisfied. If it is found in the green range, the answer range is [l, mid - 1]; [mid - 1 is because the check at this time is false, then the answer boundary must not contain mid, starting from mid - 1]; The update method is [l, r] interval, which is updated to [l, mid - 1] interval; [r = mid - 1]

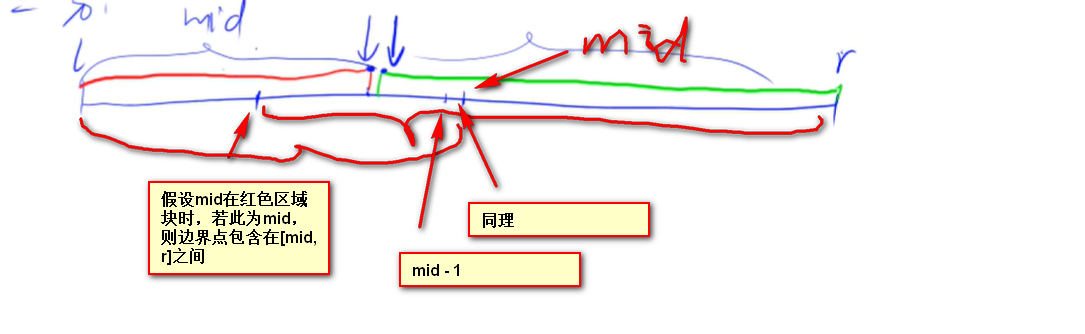
• If the above two intervals [mid is on the right half], then mid = (l + r + 1) / 2;

(2) The second case

• Suppose you want to dichotomize the green point;

• step one: let the middle point mid = (l + r) / 2 first;

• Assuming that the property is green, first check whether the mid meets the property of green, if (check(mid));

• If true, the mid is in the green block interval, and the interval where the boundary point is located is [l, mid]; [r = mid];

• If false, the mid is in the red block interval, and the interval where the boundary point is located is [mid + 1, r]; [l = mid + 1];

• If these two intervals [mid is on the left half], then mid = (l + r) / 2;

• (rounding under integer division in C + +)

(3) Steps

• First: think of a mid first;
• second: write a check function to update the interval according to the check condition; [if l = mid & R = mid - 1, then mid = (l + r + 1) / 2], [if r = mid & L = mid + 1, then mid = (L + R) / 2]
• third: calculate the mid according to the division of interval;

(4) Example: ACwing 789 number range

Given a length in ascending order n An array of integers, and q Queries.

For each query, one element is returned k Start and end positions of the (positions are counted from 0).

Returns if the element does not exist in the array -1 -1. 

Input format
 The first line contains integers n and q，Represents the length of the array and the number of queries.

The second line contains n Integer (all in 1)∼10000 Range), representing the complete array.

next q Rows, each containing an integer k，Represents a query element.

Output format
 common q Line, each line contains two integers, indicating the starting position and ending position of the requested element.

Returns if the element does not exist in the array -1 -1. 

Data range
1≤n≤100000
1≤q≤10000
1≤k≤10000
 Input sample:
6 3
1 2 2 3 3 4
3
4
5
 Output example:
3 4
5 5
-1 -1

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 10;
int n, m;
int q[N];

int main ()
{
	scanf ("%d%d",&n, &m);
	for (int i = 0; i < n; ++i)
	{
		scanf ("%d", &q[i]);
	}
	// The starting and ending positions of the number to find	
	while (m--)
	{
		int x;
		scanf ("%d", &x); 
		
		// Range of initial interval 
		int l = 0, r = n - 1;
		// Find starting position boundary
		// Think about the check function 
		while (l < r)
		{
			int mid = l + r >> 1;
			//Array ascending order 
			// If the value of q[mid] is greater than x, then x is on the left half and r = mid 
			if (q[mid] >= x) r = mid;
			else l = mid + 1;	
		} 
		
		// New l == r 
		//Out of the loop, if= x has no such number 
		if (q[l] != x) cout << "-1 -1" << endl;
		else 
		{
			cout << l << ' ';
			int l = 0;
			int r = n - 1;
			while (l < r)
			{
				int mid = l + r + 1>> 1;
				// If the end position is found, change a check judgment; [look at mid after that] 
				// If true, the boundary point is on the right half 
				if (q[mid] <=x)
				{
					l = mid; 
				}else r = mid - 1; //Then the front int mid = L + R + 1 > > 1; 
			}
			// In fact, out of the loop, l and r will meet
			cout << l << endl; 
		} 
	}
	return 0;	
} 

(5) The main idea of dichotomy

	Within an interval, divide our boundary in two, and [abbreviate the length by half every time] each time, select the interval where the answer is located for the next step;(Every time, we can ensure that there are answers in our interval, and the answers will be covered by the interval)
    When our interval is 1, the number in this interval must be the answer;
    Bisection (template) must be solvable; No solution is relative to the problem, for example ACwing 789 This is an example; (the property defined by us must have a boundary, and it can be divided into two parts)     

2. Floating point binary

(1) Take the square root as an example

//take a square root 
#include <bits/stdc++.h>
using namespace std;

int main()
{
	// Enter the number of square roots to be found 
	double x;
	cin >> x;
	
//	Determine boundary 
	double l = 0;
	double r = x; 
//	Because it is a floating point number, it cannot be simply used= 
//	Jump out of loop when R - L < = 1e-8 considers "equal" 
	while (r - l > 1e-8)
	{
		double mid = (l + r) / 2; //Find the mid first
		if (mid * mid >= x)
		{
//			It shows that the square root is smaller than mid on the left half, but mid can be obtained if it is satisfied
			r = mid; 
		} 
		else 
		{
//			Otherwise, just let l = mid, because it's a floating point number
			l = mid; 
		}
	} 
//	%lf is 6 digits by default, so the front is 1e-8 (two digits more than the number to be retained, which is safer) 
	printf ("%lf", l);
}