sort

Quick sort
The core idea of fast platoon is divide and conquer. Choose one as a sentry, so that the number less than or equal to it is on the left and the number greater than or equal to it is on the right
The time complexity is n(logn)

The steps are roughly divided into the following three steps:

• Determine the dividing point
• Adjustment interval
• Recursive processing of left and right segments

y God template:

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;//The number of elements is one

    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

General template:

#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1e6+10;

int n;
int a[N];

void quick_sort(int q[],int l,int r)
{
    if(l>=r) return;
    int i=l-1,j=r+1,x=q[l+r>>1];
    while(i<j)
    {
        do i++;while(q[i]<x);
        do j--;while(q[j]>x);
        if(i<j) swap(q[i],q[j]);
    }

    quick_sort(q,l,j);quick_sort(q,j+1,r);
}
int  main(void)
{
    scanf("%d",&n);
    
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    
    quick_sort(a,0,n-1);
    for(int i=0;i<n;i++) printf("%d ",a[i]);
    return 0;
}

Merge sort
The core idea of fast platoon is divide and conquer, but it takes the middle position as the dividing point, which is different from fast platoon. Fast platoon selects a number in the array as the dividing point.
The time complexity is n(logn)

The steps are roughly divided into three steps:

• Determine the dividing point
• Recursive sorting
• Merge (merge into one)

y God template:

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

General template:

#include<cstdio>
using namespace std;
const int N=100010;
int a[N];
int tmp[N];
void merge_sort(int q[],int l,int r)
{
	if(l>=r) return;//The description has been divided into one by one
	int mid=l+r>>1;
	merge_sort(q,l,mid),merge_sort(q,mid+1,r);
	
	int k=0;
	int i=l;//Head of left section 
	int j=mid+1; //Head of right section
	while(i<=mid&&j<=r)
	{
		if(q[i]<=q[j]) tmp[k++]=q[i++];
		else tmp[k++]=q[j++];
	} 
	while(i<=mid) tmp[k++]=q[i++];
	while(j<=r) tmp[k++]=q[j++];
	for(i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];
}
int main(void)
{
	int n; scanf("%d",&n);
	for(int i=0;i<n;i++) scanf("%d",&a[i]);
	merge_sort(a,0,n-1);
	for(int i=0;i<n;i++) printf("%d ",a[i]);
	puts("");
	return 0;
}

Dichotomy

Integer dichotomy

If the integer is divided into two parts, we can judge whether r=mid or l=mid according to check()
Use this method to judge whether to add 1

y God template:

bool check(int x) {/* ... */} // Check whether x meets certain properties

// The interval [l, r] is divided into [l, mid] and [mid + 1, r]:
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check() determines whether the mid satisfies the property
        else l = mid + 1;
    }
    return l;
}
// The interval [l, r] is divided into [l, mid - 1] and [mid, r]:
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

Floating point binary

For the floating-point binary template, there is no need to judge whether to add 1 or not, because it is continuous.

y God template:

bool check(double x) {/* ... */} // Check whether x meets certain properties

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps indicates accuracy, which depends on the accuracy requirements of the subject
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

high-precision

High precision addition

y God template:

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
    if (A.size() < B.size()) return add(B, A);

    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }

    if (t) C.push_back(t);
    return C;
}

vector<int> add(vector<int> &A,vector<int> &B)
{
    vector<int> C;
    int t=0;
    for(int i=0;i<A.size()||i<B.size();i++)
    {
        if(i<A.size()) t+=A[i];
        if(i<B.size()) t+=B[i];
        C.push_back(t%10);
        t/=10;
    }
    if(t) C.push_back(1);
    return C;
}

High precision subtraction

y God template:

// C = A - B, satisfying a > = B, a > = 0, b > = 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

Complete instance:

#include<iostream>
#include<cstdio>
#include<string>
#include<vector>
using namespace std;
bool cmp(vector<int> &A,vector<int> &B)
{
    if(A.size()>B.size()) return true;
    if(A.size()<B.size()) return false;
    for(int i=A.size()-1;i>=0;i--)
    {
        if(A[i]>B[i]) return true;
        if(A[i]<B[i]) return false;
    }
    return true;
}
vector<int> sub(vector<int> &A,vector<int> &B)
{
    vector<int> C;
    int t=0;
    for(int i=0;i<A.size();i++)
    {
        t=A[i]-t;
        if(i<B.size()) t=t-B[i];
        C.push_back( (t+10) %10);
        if(t<0) t=1;
        else t=0;
    }
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;
}
int main(void)
{
    string a,b; cin>>a>>b;
    vector<int>A,B;
    for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
    if(cmp(A,B))
    {
        auto C=sub(A,B);
        for(int i=C.size()-1;i>=0;i--) cout<<C[i];
    }
    else
    {
        auto C=sub(B,A);
        cout<<"-";
        for(int i=C.size()-1;i>=0;i--) cout<<C[i];
    }
}

High precision multiplication

y God template:

// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}

High precision Division

Note that division is different from others. We calculate from low to high.
Division is calculated from high position to high position.

y God template:

// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

Prefix and

One dimensional prefix sum

y God template:

S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

Complete code:

#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e5+10;
int a[N];
int s[N];
int main(void)
{
    int n,m; cin>>n>>m;
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];
    while(m--)
    {
        int l,r; cin>>l>>r;
        cout<<s[r]-s[l-1]<<endl;
    }
    return 0;
}

2D prefix and

y God template:

S[i, j] = The first i that 's ok j The sum of all elements in the upper left part of the column grid
 with(x1, y1)Is the upper left corner,(x2, y2)The sum of the submatrix in the lower right corner is:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

Complete code:

#include<cstdio>
#include<iostream>
using namespace std;
const int N=1010;
int n,m,q;
int a[N][N],s[N][N];
int main(void)
{
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			scanf("%d",&a[i][j]);
			s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
		}
	}
	while(q--)
	{
		int x1,y1,x2,y2;
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		printf("%d\n",s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]);
	}
	return 0;
}

Difference

Difference is an inverse operation of prefix sum.
We are going to construct an array b1,b2,b3. bring
b1=a1-a0; b2=a2-a1; b3=a3-a2;
So a1=b1=a1; a2=b1+b2=a2 a3=b3+b2+b1=a3;

If we want to add, we just need to add a c at the beginning and subtract c next to the last at the end.
Because it is a prefix and, so one plus a number, the others will be added

One dimensional difference
y God template:

Give interval[l, r]Each number in the plus c: B[l] += c, B[r + 1] -= c

Full code:

#include<iostream>
#include<cstdio>
using namespace std;
const int N=101000;
int a[N],b[N];
void insert(int l,int r,int c)
{
    b[l]+=c;
    b[r+1]-=c;
}
int main(void)
{
    int n,m;cin>>n>>m;
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    
    for(int i=1;i<=n;i++) insert(i,i,a[i]);//Initialize differential array
    
    while(m--)
    {
        int l,r,c; cin>>l>>r>>c;
        insert(l,r,c);
    }
    for(int i=1;i<=n;i++) b[i]+=b[i-1];//Prefix Sum 
    
    for(int i=1;i<=n;i++) cout<<b[i]<<" ";
    return 0;
}

Two dimensional difference

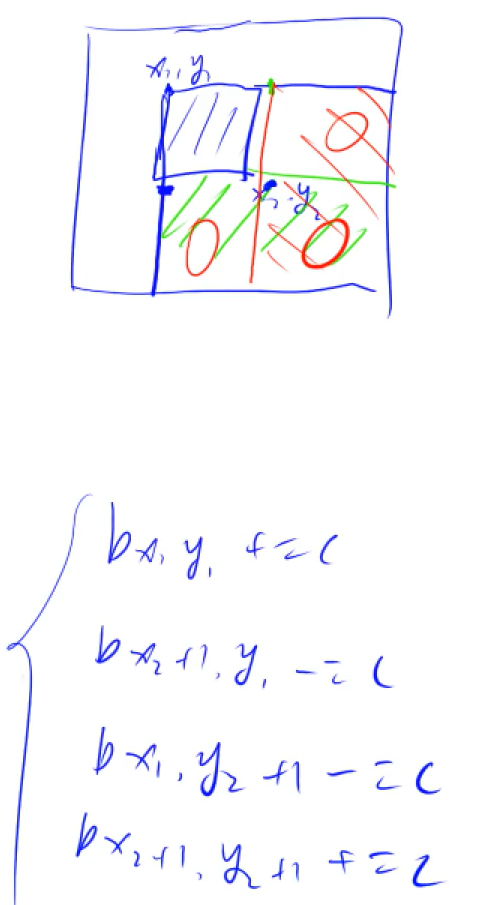
y God template:

Give(x1, y1)Is the upper left corner,(x2, y2)Add to all elements in the submatrix in the lower right corner c: 
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

Full code:

#include<iostream>
#include<cstdio>
using namespace std;
const int N=1010;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}
int main(void)
{
    int n,m,q;cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&a[i][j]);
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            insert(i,j,i,j,a[i][j]);//initialization
        }
    }
    
    while(q--)
    {
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        insert(x1,y1,x2,y2,c);
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];//Prefix and
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            cout<<b[i][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}

Binary

y God template:

seek n The first k Digit number: n >> k & 1
 return n Last 1: lowbit(n) = n & -n

Double pointer

y God template:

for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;

    // Logic of specific problems
}
Classification of frequently asked questions:
    (1) For a sequence, maintain an interval with two pointers
    (2) For two sequences, maintain a certain order, such as merging two ordered sequences in merge sort

Discretization

y God template:

vector<int> alls; // Store all values to be discretized
sort(alls.begin(), alls.end()); // Sort all values
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // Remove duplicate elements

// Find the discretized value corresponding to x by bisection
int find(int x) // Find the first position greater than or equal to x
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // Map to 1, 2 n
}

Interval merging

y God template:

// Merge all intersecting intervals
void merge(vector<PII> &segs)
{
    vector<PII> res;

    sort(segs.begin(), segs.end());

    int st = -2e9, ed = -2e9;
    for (auto seg : segs)
        if (ed < seg.first)//Merge in the same way
        {
            if (st != -2e9) res.push_back({st, ed});//Not the initial value
            st = seg.first, ed = seg.second;
        }
        else ed = max(ed, seg.second);//merge

    if (st != -2e9) res.push_back({st, ed});//Last interval

    segs = res;
}