1. Algorithm idea

1. Problems solved

Dijkstra algorithm is an algorithm based on greed. Its purpose is to solve the single source shortest path problem of positive weight graph.
The so-called positive weight means that the weight of all edges in the graph is positive. The so-called single source shortest path is the shortest path from a starting point to any position in the graph.
When using Dijkstra algorithm, if it is a sparse graph (the order of magnitude of edges is less than the square of points), it is best to use heap optimized Dijkstra. If it is a dense graph, that is (m ~ n) ²) Then you can continue to use the naive Dijkstra algorithm.

2. Specific small examples

It's not intuitive to say empty words. It's better to look at a small example first.
In the initial state, except the starting point, the shortest distance from all other points to the starting point is set to positive infinity.

From all points (including the starting point), find a point (marked) that has not been updated as the point closest to the starting point and is closest to the starting point. Obviously, in the current case, it is the starting point itself, in this example, point 4. Use the selected point closest to the starting point to update all points (1, 2, 3) that are not marked and can be reached by the node The distance to the starting point. The specific update methods are:
For example, for node 3, compare the shortest distance from 3 to the starting point (positive infinity) with the distance from 3 to the point closest to the starting point plus the distance from the point closest to the starting point to the starting point, and select the shorter one to update. Here is positive infinity and 1 (3 to 4) + 0 (4 to 4) After comparison, the result is to update 3 to 1, and the same is true for other nodes. After the update, mark point 4.

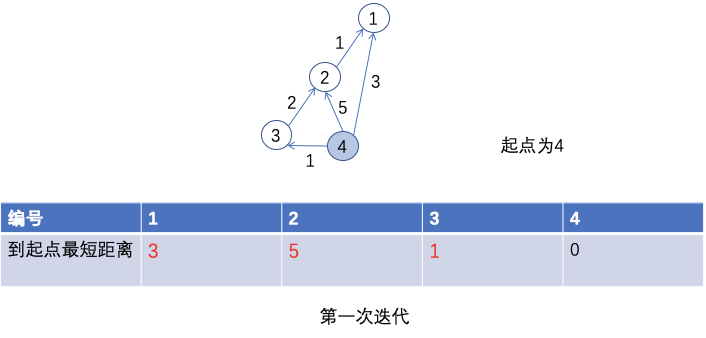
In the second iteration, similarly, from all points (including the starting point), find a point that has not updated other nodes as the point closest to the starting point (that is, the marked point) And the point closest to the starting point. The starting point has already made this point, so we choose point 3. We use node 3 to update the points it can reach and are not marked. There is only node 2. Compare the shortest distance 3 from node 2 to the starting point with the distance from node 2 to node 3 plus the distance from node 3 to the starting point (compare 5 and 2 + 1) Update the minimum distance of 2 to 3.

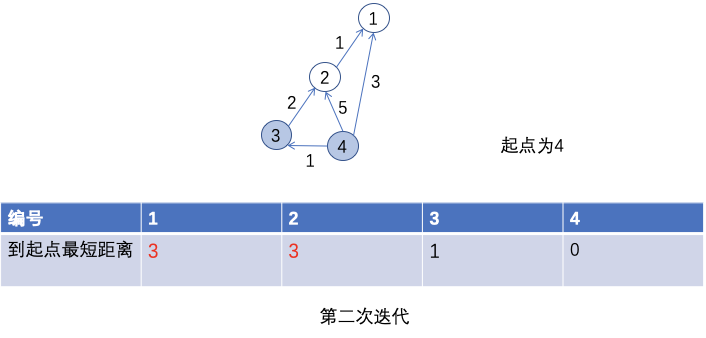
This iterates until all nodes are marked, and the shortest distance from the starting point to all other points is obtained.

3. Heap optimized Dijkstra algorithm

We write the pseudo code of the above naive Dijkstra algorithm as follows

for i: 1- n
    t <- Unmarked point closest to the starting point	Step 1
    take t sign							Step 2
    use t To update the distance of other points		        Step 3

Time complexity of naive Dijkstra algorithm O ( n 2 ) O(n^2) O(n2)
Among them, step 1 of each cycle is executed in total n 2 n^2 n2 times (n is the number of points), and all cycle steps 3 are executed m times in total (M refers to the number of edges, which is stored in the adjacency table. Each T will only reach the points it can reach, and the total sum of all t is the number of edges) It can be seen that the most time-consuming step is step 1, and step 1 is to find the smallest one in a pile of numbers, so we can use the heap to optimize this step.
In this way, the minimum value can be found only by using the time of O(1) in step 1. When adjusting in step 3, we know that the time complexity of heap adjustment is O(logn), and step 3 will be executed m times in total, so the time complexity of Dijkstra algorithm in heap optimization version will become O ( m l o g n ) O(mlogn) O(mlogn)
Therefore, when using Dijkstra algorithm, if it is a sparse graph (the order of magnitude of edges is less than the square of points), it is best to use heap optimized Dijkstra. If it is a dense graph, that is (m ~ n) ²) Then you can continue to use the naive Dijkstra algorithm.

2. Examples

The following two examples demonstrate the naive Dijkstra algorithm and its heap optimization version respectively

1.Dijkstra finding the shortest path I

Given a n Points m In a directed graph with edges, there may be multiple edges and self rings, and all edge weights are positive.

Please find out the arrival time on the 1st n The shortest distance from point 1. If you can't walk from point 1 n Point, output −1. 

Input format
 The first line contains integers n and m. 

next m Each row contains three integers x,y,z，Indicates that there is a slave point x To point y The directed edge of is z. 

Output format
 Output an integer representing point 1 to n The shortest distance of point.

Output if the path does not exist −1. 

Data range
1≤n≤500,
1≤m≤10^5,
The side length involved in the figure shall not exceed 10000.

Input example:
3 3
1 2 2
2 3 1
1 3 4
 Output example:
3

As you can see, this is a dense graph, so we use a simple algorithm

#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10;

int e[N],ne[N],h[N],idx,w[N];
int d[510],n,m;
bool st[510];

void add(int a, int b, int v)
{
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = v;
    h[a] = idx ++;
}

int dj()
{
    memset(d,0x3f,sizeof d);
    d[1] = 0;
    for(int i = 0; i < n; i ++)
    {
        int u = -1, min = 0x3f3f3f3f;
        for(int i = 1; i <= n; i ++)
        {
            if(d[i] < min && !st[i])
            {
                min = d[i];
                u = i;
            }
        }
        if(u == -1)break;
        st[u] = true;
        for(int i = h[u]; i != -1; i = ne[i])
        {
            if(d[e[i]] > d[u] + w[i])
            {
                d[e[i]] = d[u] + w[i];
            }
        }
    }
    if(d[n] == 0x3f3f3f3f)return -1;
    else return d[n];
}
int main()
{
    cin >> n >> m;
    memset(h,-1,sizeof h);
    for(int i = 0; i < m; i ++)
    {
        int a,b,v;
        cin >> a >> b >> v;
        add(a,b,v);
    }
    cout << dj();
}

2.Dijkstra finding the shortest path II

Given a n Points m For a directed graph with edges, there may be multiple edges and self rings, and all edge weights are non negative.

Please find out the arrival time on the 1st n The shortest distance from point 1. If you can't walk from point 1 n Point, output −1. 

Input format
 The first line contains integers n and m. 

next m Each row contains three integers x,y,z，Indicates that there is a slave point x To point y The directed edge of is z. 

Output format
 Output an integer representing point 1 to n The shortest distance of point.

Output if the path does not exist −1. 

Data range
1≤n,m≤1.5×10^5,
The side length involved in the figure is not less than 0 and not more than 10000.

Input example:
3 3
1 2 2
2 3 1
1 3 4
 Output example:
3

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 2e5 + 10;
typedef pair<int,int> PII;
int e[N],ne[N],idx,h[N],w[N],d[N],n,m;
bool st[N];
void add(int a, int b, int x)
{
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = x;
    h[a] = idx ++;
}

int dj_h()
{
    memset(d,0x3f,sizeof d);
    d[1] = 0;
    priority_queue<PII,vector<PII>, greater<PII>> q;
    q.push({0,1});
    while(q.size())
    {
         auto t = q.top();
         int s = t.second;
         q.pop();
         if(st[s])continue;
         else st[s] = true;
         
         for(int i = h[s]; i != -1; i = ne[i])
         {
             if(d[e[i]] > d[s] + w[i])
             {
                 d[e[i]] = d[s] + w[i];
                 q.push({d[e[i]],e[i]});
             }
         }
    }
    if(d[n] == 0x3f3f3f3f) return -1;
    else return d[n];
}

int main()
{
    cin >> n >> m;
    memset(h,-1,sizeof h);
    for(int i = 0; i < m; i ++)
    {
        int a,b,x;
        cin >> a >> b >> x;
        add(a,b,x);
    }
    int ans = dj_h();
    cout << ans;
}

reference material

1. Data structure and algorithm analysis C language description (Second Edition) 9.3.2
2. Acwing