A Graph is composed of a finite non empty set of vertices and a set of edges between vertices. It is usually expressed as: G(V,E), where g represents a Graph, V is the set of vertices in Graph G, and E is the set of edges in Graph G.

Graph is a more complex data structure than linear table and tree. In the graph structure, the relationship between nodes can be arbitrary, and any two elements in the graph may be related.

1. In the linear table, we call the data element element element, in the tree, we call the data element node, and in the graph, we call it Vertex.

2. A linear table can have no data elements, which is called an empty table. There can be no nodes in the tree, which is called an empty tree. In a graph structure, no vertices are allowed. In the definition, if V is a set of vertices, it is emphasized that the vertex set V is finite and non empty.

3. In the linear table, there is a linear relationship between adjacent data elements. In the tree structure, the nodes of two adjacent layers have a hierarchical relationship. In the graph, there may be a relationship between any two vertices. The logical relationship between vertices is represented by edges, and the edge set can be empty.

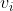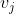Undirected edge: if vertexreachIf there is no direction between the edges, this Edge is called an undirected Edge, using unordered pairs(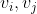)To show. If the edges between any two vertices in a graph are undirected edges, the graph is called Undirected graphs.

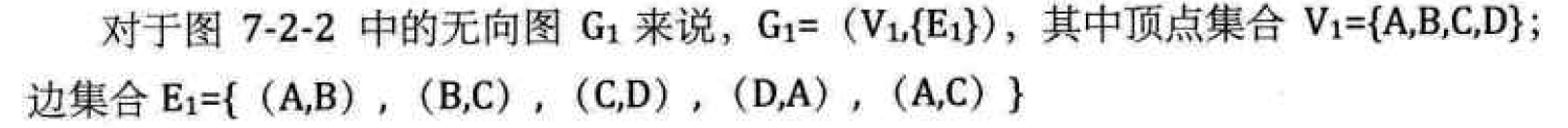
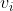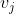Directed edge: if from vertexreachIf the edge of has a direction, it is called a directed edge, also known as Arc. Using ordered pairs<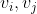>To show,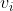Called Tail,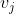It is called Head. If the edges between any two vertices in a graph are directed edges, the graph is called Directed graphs. The directed edge connecting vertices a to D is an arc, a is the tail of the arc, D is the Head of the arc, < A, d > represents the arc, note that it cannot be written as < D, a >.

In a graph, if there is no edge from the vertex to itself, and the same edge does not appear repeatedly, such a graph is called a simple graph.

In an undirected graph, if there are edges between any two vertices, the graph is called undirected complete graph. Undirected complete graph with n vertices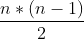Edge.

In a directed graph, if there are two arcs with opposite directions between any two vertices, the graph is called a directed complete graph. Directed complete graph with n vertices × (n-1) edge.

A graph with few edges or arcs is called a sparse graph, and vice versa is called a dense graph.

Relationship between vertices and edges of Graphs

Related terms of connected graph:

A polar connected subgraph in an undirected graph is called a connected component. It emphasizes:

1. Sub graph

2. If the subgraph is connected

3. Connected subgraphs contain maximum vertex points

4. A connected subgraph with a maximum number of vertices contains all edges attached to these vertices.

Abstract data type of graph

ADT chart(Graph)

Data
    Finite nonempty sets of vertices and sets of edges
Operation
    CreateGraph(*G,V,VR):By vertex set V Edge arc set VR Definition and construction diagram of G. 
    DestroyGraph(*G):chart G Destroy if present
    LocateVex(G,u):Ruo Tu G There are vertices in the u，Then return to the position in the figure.
    GetVex(G,v):Return graph G Middle vertex v Value of
    PutVex(G,v,value):Will figure G Middle vertex v assignment value. 
    FirstAdjVex(G,*v):Return vertex v An adjacent vertex of if the vertex is G Returns NULL if there are no adjacent vertices in the.
    NextAdjVex(G,v,*w):Return vertex v Relative to vertex w Next adjacent vertex of, if w yes v The last adjacency point of returns "null".
    InsertVex(*G,v):In Figure G Add new vertices to v. 
    DeleteVex(*G,v):Delete graph G Middle vertex v Arc and its correlation.
    InsertArc(*G,v,w):In Figure G Medium addition<v,w>,if G It is an undirected graph and needs to add symmetrical arcs<w,v>. 
    DeleteArc(*G,v,w):In Figure G Delete in<v,w>,if G If it is an undirected graph, the symmetric arc is also deleted<w,v>. 
    DFSTraverse(G):Pair graph G Depth first traversal is carried out in, and each vertex is called in the traversal process.
    HFSTraverse(G):Pair graph G Breadth first traversal is carried out in, and each vertex is called in the traversal process.
endADT

Storage structure of graph

Adjacency matrix:

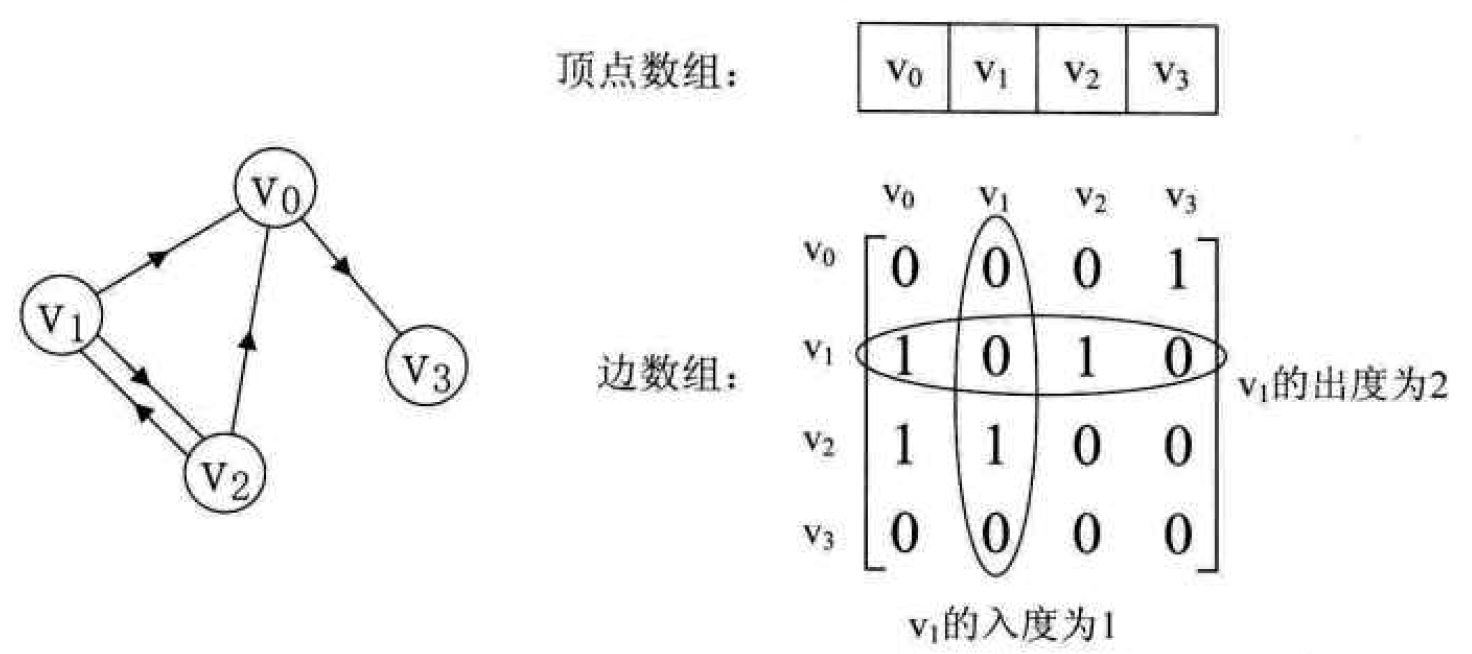
Adjacency matrix storage structure:

typedef char VertexType; /* Vertex types should be user-defined  */
typedef int EdgeType; /* The weight type on the edge shall be user-defined */
#define MAXVEX 100 / * maximum number of vertices, which shall be defined by the user*/
#define INFINITY 65535 / * use 65535 to represent ∞*/
typedef struct
{
	VertexType vexs[MAXVEX]; /* Vertex table */
	EdgeType arc[MAXVEX][MAXVEX];/* Adjacency matrix can be regarded as edge table */
	int numVertexes, numEdges; /* The current number of vertices and edges in the graph  */
}MGraph;

Undirected network diagram creation password:

/* The adjacency matrix representation of undirected network graph is established */
void CreateMGraph(MGraph *G)
{
	int i,j,k,w;
	printf("Enter the number of vertices and edges:\n");
	scanf("%d,%d",&G->numVertexes,&G->numEdges); /* Enter the number of vertices and edges */
	for(i = 0;i <G->numVertexes;i++) /* Read the vertex information and establish the vertex table */
		scanf(&G->vexs[i]);
	for(i = 0;i <G->numVertexes;i++)
		for(j = 0;j <G->numVertexes;j++)
			G->arc[i][j]=INFINITY;	/* Adjacency matrix initialization */
	for(k = 0;k <G->numEdges;k++) /* Read the edges of numEdges and establish the adjacency matrix */
	{
		printf("Input edge(vi,vj)Subscript on i，subscript j And right w:\n");
		scanf("%d,%d,%d",&i,&j,&w); /* Input weight w on edge (vi,vj) */
		G->arc[i][j]=w; 
		G->arc[j][i]= G->arc[i][j]; /* Because it's an undirected graph, the matrix is symmetric */
	}
}

From the code, we can get that the creation of undirected network graph with n vertices and e edges has a time complexity of O(n+n) ²+ e) , where the initialization of adjacency matrix Garc takes O(n ²) Time of day.  

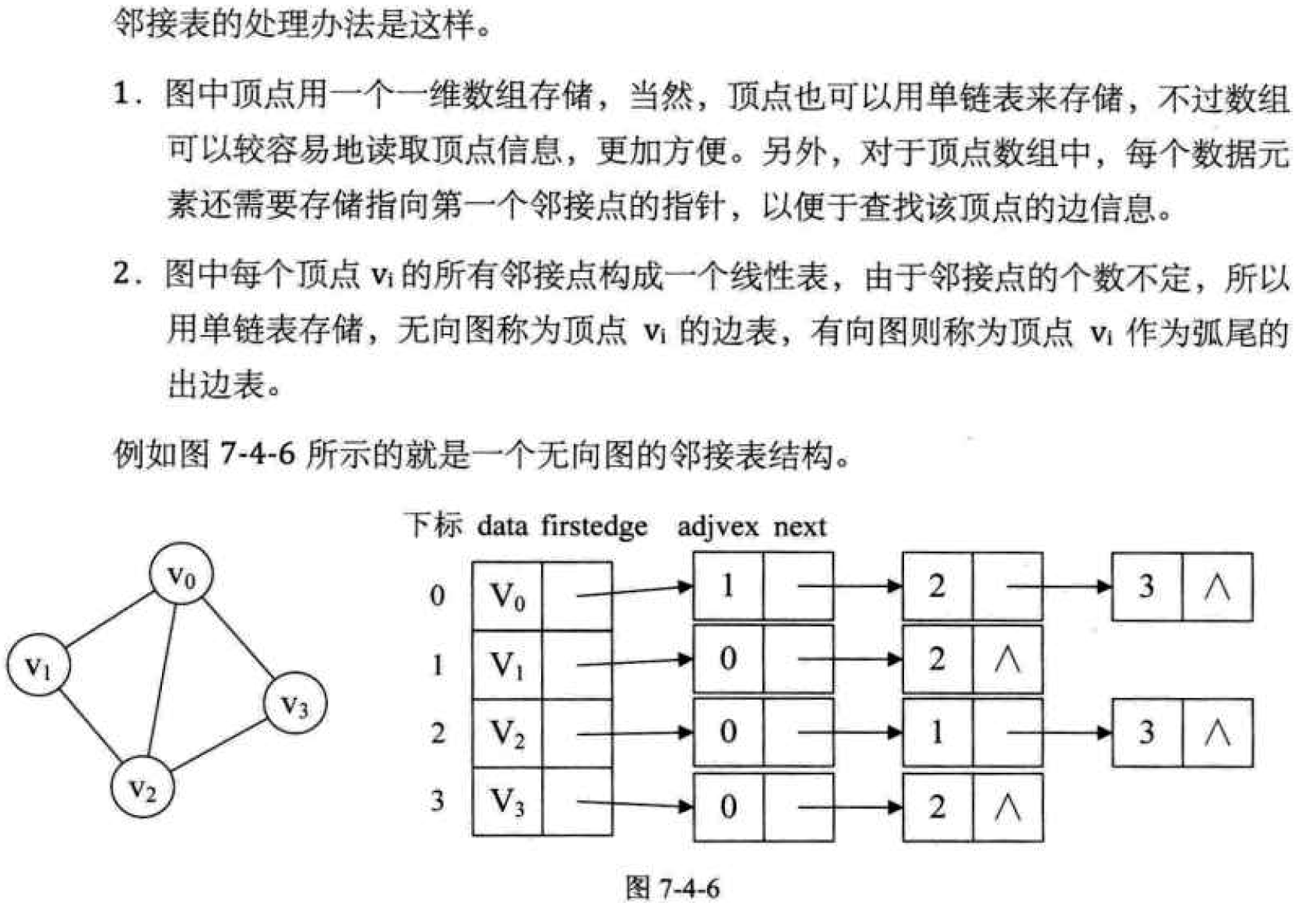
Adjacency table:

Adjacency matrix is a good graph storage structure, but for graphs with fewer edges than vertices, this structure is a great waste of storage space.

We call the storage method of this combination of array and linked list as Adjacency List.

 

 

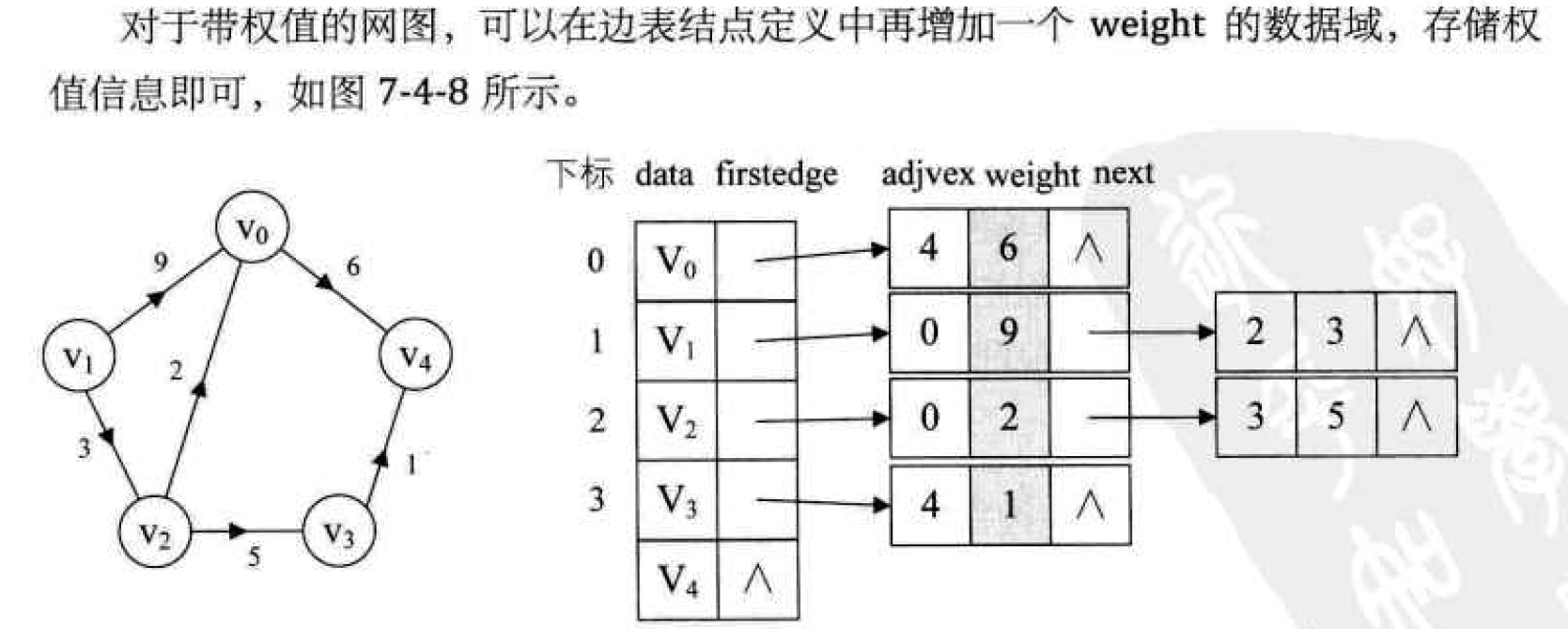
typedef char VertexType; /* Vertex types should be user-defined */
typedef int EdgeType; /* The weight type on the edge shall be user-defined */

typedef struct EdgeNode /* Edge table node  */
{
	int adjvex;    /* The adjacent point field stores the subscript corresponding to the vertex */
	EdgeType weight;		/* It is used to store weights. It is unnecessary for non network graphs */
	struct EdgeNode *next; /* Chain domain, pointing to the next adjacent node */
}EdgeNode;

typedef struct VertexNode /* Vertex table node */
{
	VertexType data; /* Vertex domain, storing vertex information */
	EdgeNode *firstedge;/* Side header pointer */
}VertexNode, AdjList[MAXVEX];

typedef struct
{
	AdjList adjList; 
	int numNodes,numEdges; /* The current number of vertices and edges in the graph */
}GraphAdjList;

Adjacency table creation of undirected graph:

/* Establish the adjacency table structure of graph */
void  CreateALGraph(GraphAdjList *G)
{
	int i,j,k;
	EdgeNode *e;
	printf("Enter the number of vertices and edges:\n");
	scanf("%d,%d",&G->numNodes,&G->numEdges); /* Enter the number of vertices and edges */
	for(i = 0;i < G->numNodes;i++) /* Read the vertex information and establish the vertex table */
	{
		scanf(&G->adjList[i].data); 	/* Enter vertex information */
		G->adjList[i].firstedge=NULL; 	/* Set the edge table as an empty table */
	}
	
	
	for(k = 0;k < G->numEdges;k++)/* Create edge table */
	{
		printf("Input edge(vi,vj)Vertex sequence number on:\n");
		scanf("%d,%d",&i,&j); /* Enter the vertex sequence number on the edge (vi,vj) */
		e=(EdgeNode *)malloc(sizeof(EdgeNode)); /* Apply for space from memory and generate edge table nodes */
		e->adjvex=j;					/* Adjacency serial number is j */                         
		e->next=G->adjList[i].firstedge;	/* Point the pointer of e to the node on the current vertex */
		G->adjList[i].firstedge=e;		/* Point the pointer of the current vertex to e */               
		
		e=(EdgeNode *)malloc(sizeof(EdgeNode)); /* Apply for space from memory and generate edge table nodes */
		e->adjvex=i;					/* Adjacency serial number is i */                         
		e->next=G->adjList[j].firstedge;	/* Point the pointer of e to the node on the current vertex */
		G->adjList[j].firstedge=e;		/* Point the pointer of the current vertex to e */               
	}
}

Cross linked list

The combination of adjacency list and inverse adjacency list is: Orthogonal List

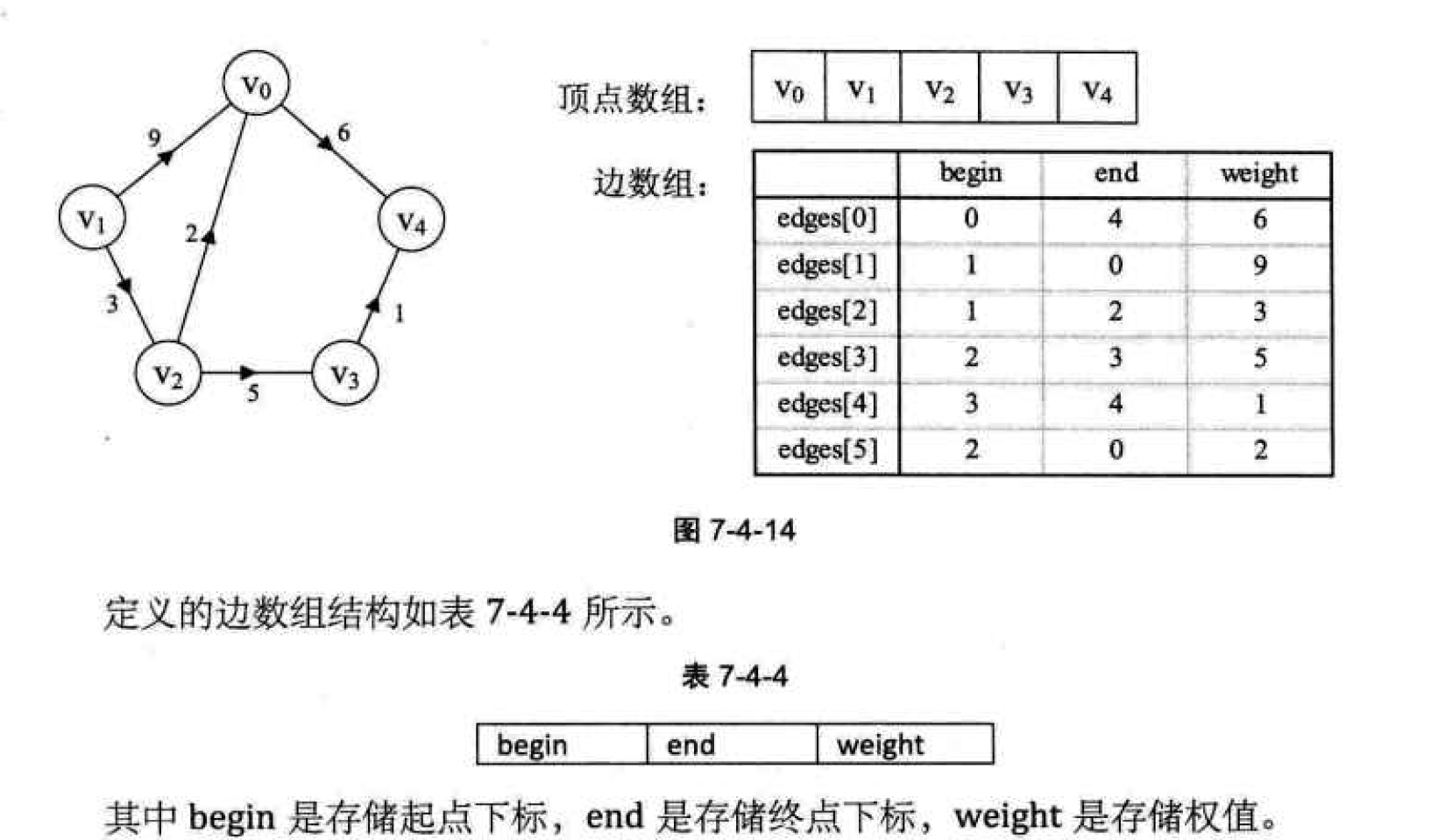
Edge set array:

Edge set array is composed of two one-dimensional arrays. One is to store the information of vertices; The other is to store the information of the edge. Each data element of the edge array is composed of the start subscript, end subscript and weight of an edge.

Traversal of Graphs

The traversal of a graph is similar to the traversal of a tree. We want to start from a vertex in the graph and visit the rest of the vertices in the graph so that each vertex is visited only once. This process is called Traversing Graph

Depth_first_search, also known as depth first search, is called DFS for short.

We use adjacency matrix:

typedef int Boolean;/*Boolean Is a boolean type whose value is True or False*/
Boolean visited[MAXVEX]; /* Array of access flags */

/* Depth first recursive algorithm for adjacency matrix */
void DFS(MGraph G, int i)
{
	int j;
 	visited[i] = TRUE;
 	printf("%c ", G.vexs[i]);/* Print vertices, or other operations */
	for(j = 0; j < G.numVertexes; j++)
		if(G.arc[i][j] == 1 && !visited[j])
 			DFS(G, j);/* Recursive call to adjacent vertices accessed for */
}

/* Depth traversal operation of adjacency matrix */
void DFSTraverse(MGraph G)
{
	int i;
 	for(i = 0; i < G.numVertexes; i++)
 		visited[i] = FALSE; /* Initially, all vertex states are unreachable states */
	for(i = 0; i < G.numVertexes; i++)
 		if(!visited[i]) /* DFS is called for vertices that have not been accessed. If it is a connected graph, it will be executed only once */ 
			DFS(G, i);
}

Breadth_First_Search, also known as breadth first search, or BFS for short.

/* Breadth traversal algorithm of adjacency matrix */
void BFSTraverse(MGraph G)
{
	int i, j;
	Queue Q;
	for(i = 0; i < G.numVertexes; i++)
       	visited[i] = FALSE;
    InitQueue(&Q);		/* Initialize a secondary queue */
    for(i = 0; i < G.numVertexes; i++)  /* Loop through each vertex */
    {
		if (!visited[i])	/* If it has not been accessed, it will be processed */
		{
			visited[i]=TRUE;		/* Set current vertex accessed */
			printf("%c ", G.vexs[i]);/* Print vertices, or other operations */
			EnQueue(&Q,i);		/* Queue this vertex */
			while(!QueueEmpty(Q))	/* If the current queue is not empty */
			{
				DeQueue(&Q,&i);	/* Get the queue pair element out of the queue and assign it to i */
				for(j=0;j<G.numVertexes;j++) 
				{ 
					/* Judge whether other vertices have edges with the current vertex and have not been visited  */
					if(G.arc[i][j] == 1 && !visited[j]) 
					{ 
 						visited[j]=TRUE;			/* Mark this vertex found as accessed */
						printf("%c ", G.vexs[j]);	/* Print vertex */
						EnQueue(&Q,j);				/* Queue this vertex found  */
					} 
				} 
			}
		}
	}
}

Minimum cost spanning tree

We call the Minimum Cost Spanning Tree for constructing connected networks as the Minimum Cost Spanning Tree

Prim algorithm:

        

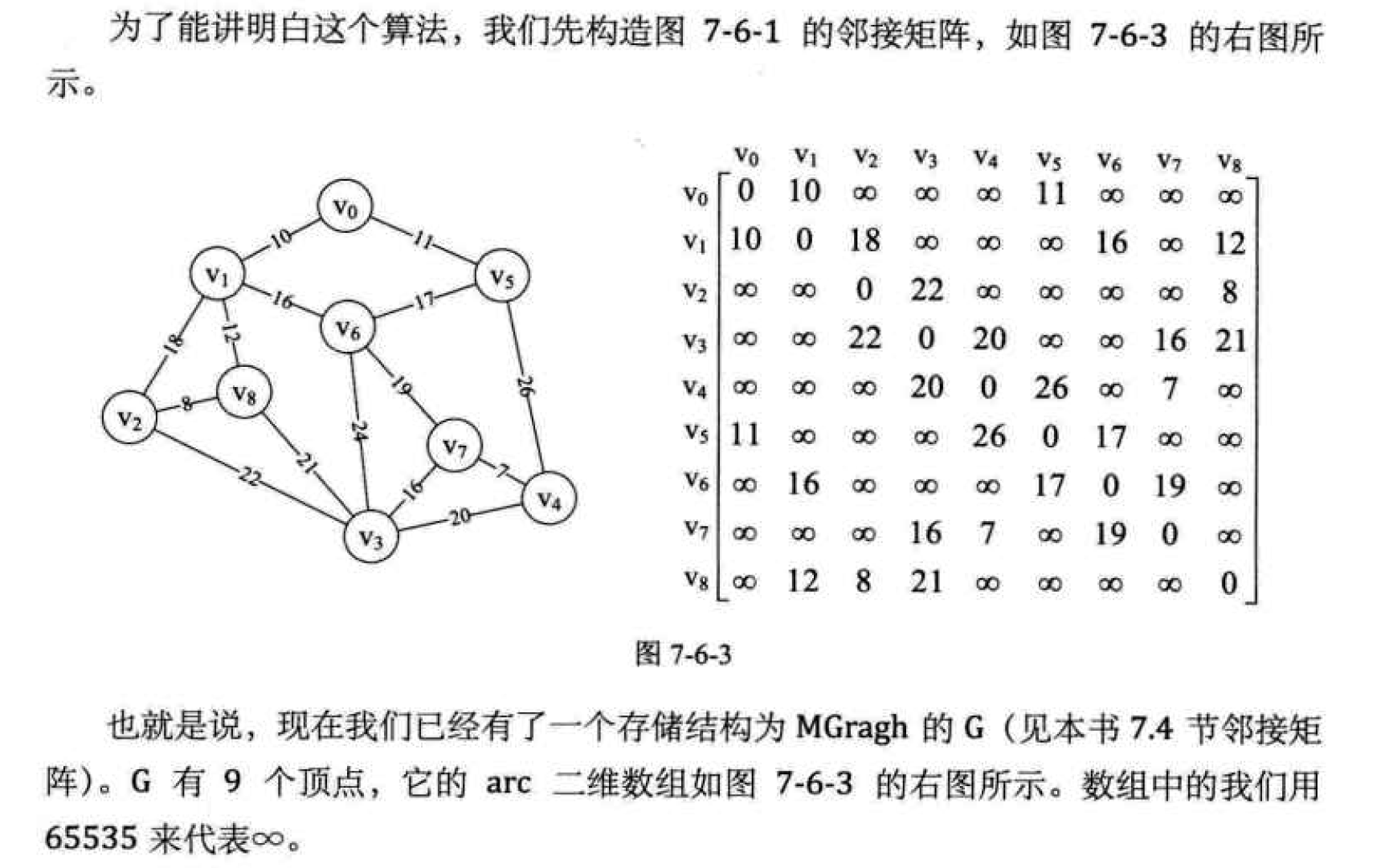
/* Prim Algorithm to generate minimum spanning tree  */
void MiniSpanTree_Prim(MGraph G)
{
	int min, i, j, k;
	int adjvex[MAXVEX];		/* Save related vertex Subscripts */
	int lowcost[MAXVEX];	/* Save the weights of edges between related vertices */
	lowcost[0] = 0;/* Initialize the first weight to 0, that is, v0 is added to the spanning tree */
			/* lowcost The value of is 0, where the vertex of this subscript has been added to the spanning tree */
	adjvex[0] = 0;			/* Initialize the first vertex with subscript 0 */
	for(i = 1; i < G.numVertexes; i++)	/* Loop all vertices except subscript 0 */
	{
		lowcost[i] = G.arc[0][i];	/* Store the weights of v0 vertices and edges in the array */
		adjvex[i] = 0;					/* Subscript initialized to v0 */
	}
	for(i = 1; i < G.numVertexes; i++)
	{
		min = GRAPH_INFINITY;	/* The minimum initialization weight is ∞, */
						/* It is usually set to an impossible large number, such as 32767, 65535, etc */
		j = 1;k = 0;
		while(j < G.numVertexes)	/* Loop all vertices */
		{
			if(lowcost[j]!=0 && lowcost[j] < min)/* If the weight is not 0 and the weight is less than min */
			{	
				min = lowcost[j];	/* Make the current weight the minimum value */
				k = j;			/* Save the subscript of the current minimum value into k */
			}
			j++;
		}
		printf("(%d, %d)\n", adjvex[k], k);/* Prints the edge with the lowest weight among the current vertex edges */
		lowcost[k] = 0;/* Set the weight of the current vertex to 0, indicating that the vertex has completed the task */
		for(j = 1; j < G.numVertexes; j++)	/* Loop all vertices */
		{
			if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j]) 
			{/* If the subscript is k, the weight of each edge of the vertex is less than the weight of the previous vertices that have not been added to the spanning tree */
				lowcost[j] = G.arc[k][j];/* Store the smaller weight in the corresponding position of lowcast */
				adjvex[j] = k;				/* Save vertices with subscript k into adjvex */
			}
		}
	}
}

Kruskal algorithm:

Unfinished