1, Four basic steps of dynamic planning:  

2, Common methods of dynamic programming:

  (1) Bottom up solution:

         The most common dp algorithm derives the optimal solution of the problem with the second smaller scale from the initial value of dp, records it in the array, and then continuously expands the problem scale to find the sub problem with a larger scale. Each time the current problem is solved, the previous solution will be used. Therefore, save the previous solutions to avoid repeated calculations for the same sub problem.

  (2) Top down solution:

         Also known as memorandum act. It can be considered as an optimized recursive algorithm. That is, open up an array space. In the recursive process, check whether the problem has been solved. If the solution has been obtained earlier, there is no need for recursion, and the solution of the sub problem can be obtained directly. Otherwise, it can be solved recursively. In essence, it is the recursive implementation of the former algorithm. In the real solution, it also solves the sub problem with the smallest scale first, and then expands the problem scale in turn. Moreover, because the program is recursive, it has to pay additional program running cost.

3, Examples of dynamic planning to solve problems:

(1) Digital triangle problem  

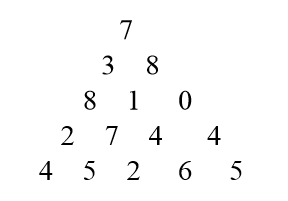
Find a path from the top to the bottom in the number triangle to maximize the sum of the numbers on the path. Each step on the path can only go down left or right. Just find the maximum sum and the path. The number of rows of triangle is greater than 1, less than or equal to 100, and the number is 0 - 99

    Input format:

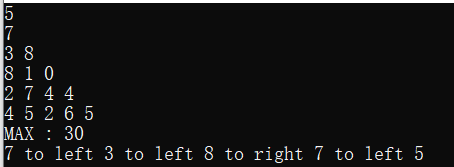
    five      // Represents the number of rows of a triangle     Next, enter the triangle

    7

    3   8

    8   1   0

    2   7   4   4

    4   5   2   6   5

    Maximum output path required

sample input

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

sample output

MAX : 30
7 to left 3 to left 8 to right 7 to left 5

analysis:

         The state transition equation of digital triangle problem is dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+a[i][j]; dp[i][j] means the maximum possible value to (i,j). According to the analysis, only the two points in the upper left corner (i-1, j-1) and the upper right corner (i-1.j) may reach the current point (i,j). Take the largest of them and add a[i][j] to get dp[i][j]. At the same time, record s [i] [J] to indicate which direction dp[i][j] is obtained from. Initialize dp[k][0], dp[k][k], s[k][0], s[k][k]   Where 0 < = k < n. Traverse the bottom dp[n-1][k] to find the maximum value. The path can be obtained by s[i][j] recursive solution.

code:

#include<iostream>

using namespace std;

int a[100][100];
int dp[100][100];
int s[100][100];

void init(int n){//dp initialization
	dp[0][0]=a[0][0];
	for(int i=1;i<n;i++){
		dp[i][i]=dp[i-1][i-1]+a[i][i];
		dp[i][0]=dp[i-1][0]+a[i][0];
		s[i][i]=-1;
		s[i][0]=1;
	}	
}

int solve(int n,int &t){//The optimal solution of each position is obtained in turn
	init(n);
	for(int i=1;i<n;i++){
		for(int j=1;j<i;j++){
			dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+a[i][j];
			if(dp[i-1][j-1]>dp[i-1][j])s[i][j]=-1;//Select with s[i][j] record
			else s[i][j]=1;
		}
	}
	int max=dp[n-1][0];
	t=0;
	for(int i=1;i<n;i++){
		if(dp[n-1][i]>max){
			max=dp[n-1][i];
			t=i;
		}
	}
	return max;//Returns the lowest optimal solution
}

void print(int i,int j){//Using s[i][j] to reconstruct the optimal solution
	if(i==0){
		cout<<a[i][j]<<' ';
		return ;
	}
	if(s[i][j]>0){
		print(i-1,j);
		cout<<"to left"<<' ';
	}
	else{
		print(i-1,j-1);
		cout<<"to right"<<' ';
	}
	cout<<a[i][j]<<' ';
}


int main(){
	int n;
	cin>>n;
	for(int i=0;i<n;i++){
		for(int j=0;j<=i;j++){
			cin>>a[i][j];
		}
	}
	
	int t;
	cout<<"MAX : "<<solve(n,t)<<endl;
	print(n-1,t);
	
	return 0;
} 

/*
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
*/

Operation results:

(2) Longest common subsequence problem:

Given two sequences X={x1,x2,..., xm} and Y={y1,y2,..., yn}, find the longest common subsequence of X and y.

Input:

The first line gives an integer n (0 < n < 100) indicating the number of data groups to be tested. Next, each group of data has two rows, which are two groups of strings to be tested. The length of each string shall not be greater than 1000.

Output:

Each group of test data outputs an integer representing the length of the longest common subsequence, and outputs the longest common subsequence at the same time.

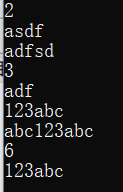
sample input

2

asdf

adfsd

123abc

abc123abc

sample output

3

adf

6

123abc

analysis:

(3) 0-1 knapsack problem

  Given n items and a backpack. The weight of item i is wi, its value is vi, and the capacity of the backpack is W. Q: how to select the items loaded into the backpack to maximize the total value of the items loaded into the backpack?

  Input: the first line has two positive integers n and W,n is the number of items, W is the backpack capacity, the next line has n positive integers, indicating the value of the item, and the third line has n positive integers, indicating the weight of the item.

     Output:

     The maximum value of the items loaded into the backpack and the optimal loading scheme will be calculated

Input example:

5 10

6 3 5 4 6

2 2 6 5 4

Output example:

  15

  1 1 0 0 1

analysis:

The state transition equation of 0-1 knapsack problem is dp[i][j] = max (dp[i-1][j], dp[i-1][j-w[i-1]] + v [i-1]); The physical meaning of dp[i][j] is to consider the maximum value of the first I items when the backpack capacity is j. Special circumstances need to be considered. If the current item exceeds the available backpack capacity, the current item will not be considered. The print function checks whether dp[i][j] and dp[i-1][j] are the same. If they are the same, it means that the ith item is not selected. If it is selected, the selection of the first i-1 items under the backpack with the capacity of j-w[i] is considered and solved recursively. Initialization: the value of the first 0 items, no matter how large the backpack is, is 0, the backpack capacity is 0, and the considered value of any item is 0.

code:

#include<iostream> 
using namespace std;

int dp[1000][1000];

void init(int n,int W){
	for(int i=0;i<=n;i++){
		dp[i][0]=0;
	}
	for(int i=0;i<=W;i++){
		dp[0][i]=0;
	}
}

void solve(int n,int W,int* w,int* v){
	for(int i=1;i<=n;i++){
		for(int j=1;j<=W;j++){
			if(w[i-1]>j){//Current item cannot be loaded 
				dp[i][j]=dp[i-1][j];
			}
			else{//Can be installed, take the best 
				dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i-1]]+v[i-1]);
			}
		}
	}
}

void print(int i,int j,int* w){
	if(i==0) return ;
	if(dp[i][j]==dp[i-1][j]){//The same means no selection 
		print(i-1,j,w);
		cout<<0<<' ';
	}
	else{//Different means you chose 
		print(i-1,j-w[i-1],w);
		cout<<1<<' ';
	}
}

int main(){
	
	int n,W; 
	cin>>n>>W;
	int v[n];//valve
	int w[n];//weight 
	for(int i=0;i<n;i++){
		cin>>v[i];
	}
	for(int i=0;i<n;i++){
		cin>>w[i];
	}

	init(n,W);
	
	solve(n,W,w,v);//Fill in a form 
	
	cout<<dp[n][W]<<endl;//Output optimal value 
	
	print(n,W,w);//Output optimal solution 


	return 0; 
}

/* 
5 10
6 3 5 4 6
2 2 6 5 4
*/

Operation results:

4, Summary:

        The most difficult part of dynamic programming is to write the correct state transition equation. We need to train more dp thinking, fully consider the relationship between the initial value of dp and the state transition between dp arrays, find the correct recursive relationship, and add the accurate boundary division of variables to obtain the state transition equation, followed by the coding process.