Chapter VIII sorting
What is sorting?
Sorting: arrange a group of disorderly data in order according to a certain law.
Learning content
Sort by principle
- Insert sort: direct insert sort, half insert sort, Hill sort
- Swap sort: bubble sort, quick sort
- Select sort: simple select sort and heap sort
- Merge sort: 2-way merge sort
- Cardinality sort
Workload required by sort
- Simple sorting method: T(n)=O(n*n)
- Cardinality sorting: T(n)=O(d.n)
- Advanced sorting method: T(n)=O(nlogn)
#define MAXSIZE 20 // Set no more than 20 records
typedef int KeyType; //Set keyword to integer
Typedef struct{ //Define the structure of each record (data element)
KeyType key; //keyword
InfoType otherinfo; //Other data items
}RedType;
Typedef struct{ //Defines the structure of the sequence table
RedType r [MAXSIZE+1] //Vector of storage order table
//r[0] is usually used as a sentry or buffer
int length; //Length of sequence table
}SqlList
8.1 insert sort
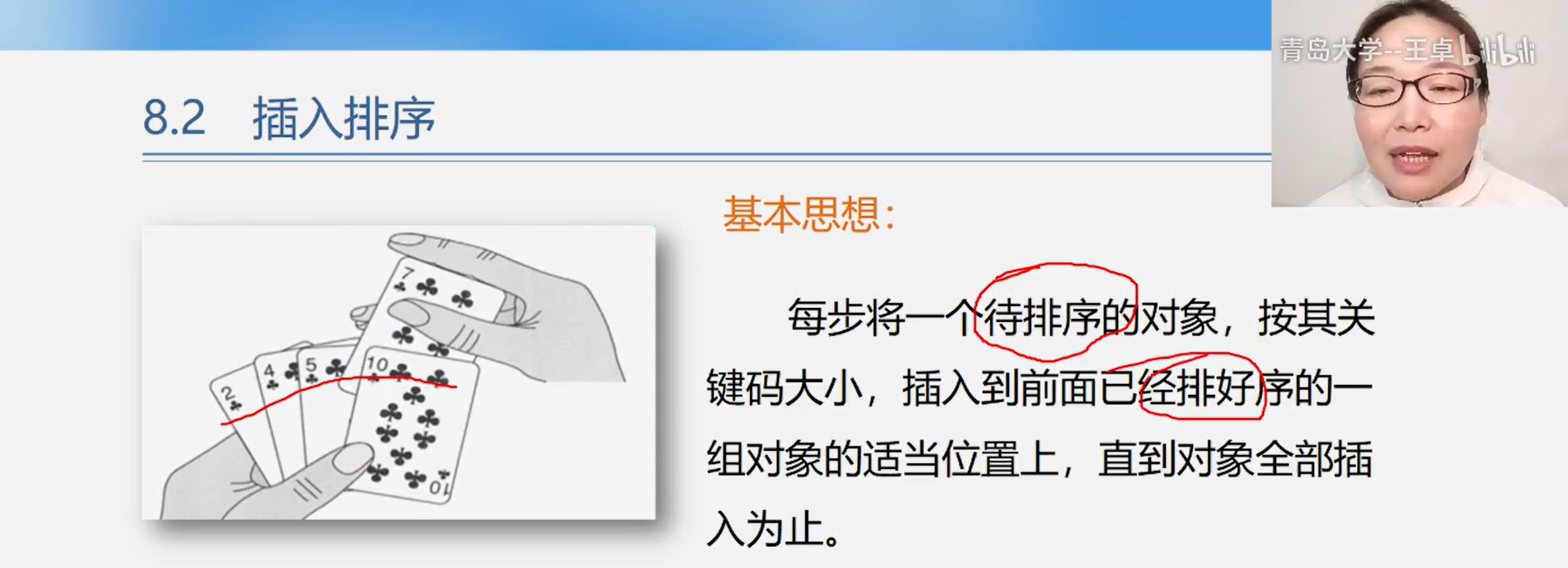
Insert sort type

Direct insert sort
Original direct insert sort


Direct insertion sort using sentinel

void InsertSort(SqList &L){
int i,j;
for(i=2;i<L.length;i++){
if(L.r[i].key < L.r[i-1].key){//If <, insert L.r[i] into the ordered sub table
L.r[0] = L.r[i]; //Copy as sentinel
for(j=i-1;L.r[0].key<L.r[j].key;--j){
L.r[j+1]=L.r[j];//Record backward
}
L.r[j+1]=L.r[0]; //Insert in the correct position
}
}
}
performance analysis


Time complexity conclusion
The closer the original data is to order, the faster the sorting speed is
In the worst case (the input data is inversely ordered) Tw(n)=O(n*n)
On average, the time consumption is almost half of the worst case, Te(n)=O(n*n)
To improve search speed
- Reduce the number of element comparisons
- Reduce the number of element moves
Binary Insertion Sort


Algorithm analysis:

The object movement times of half insertion sort are the same as that of direct insertion sort, which depends on the initial arrangement of objects
- The number of comparisons is reduced, but the number of moves is not reduced
- The average performance is better than direct insertion sorting
The time complexity is O(n*n)
Space complexity O(1)
It is a stable sorting method
Shell Sort
Basic idea: first, the whole record sequence to be arranged is divided into several subsequences for direct insertion sorting. When the records in the whole sequence are "basically orderly", all records are directly inserted and sorted in turn.
Hill sorting algorithm features:
- Reduce increment
- Polytropic insertion sort
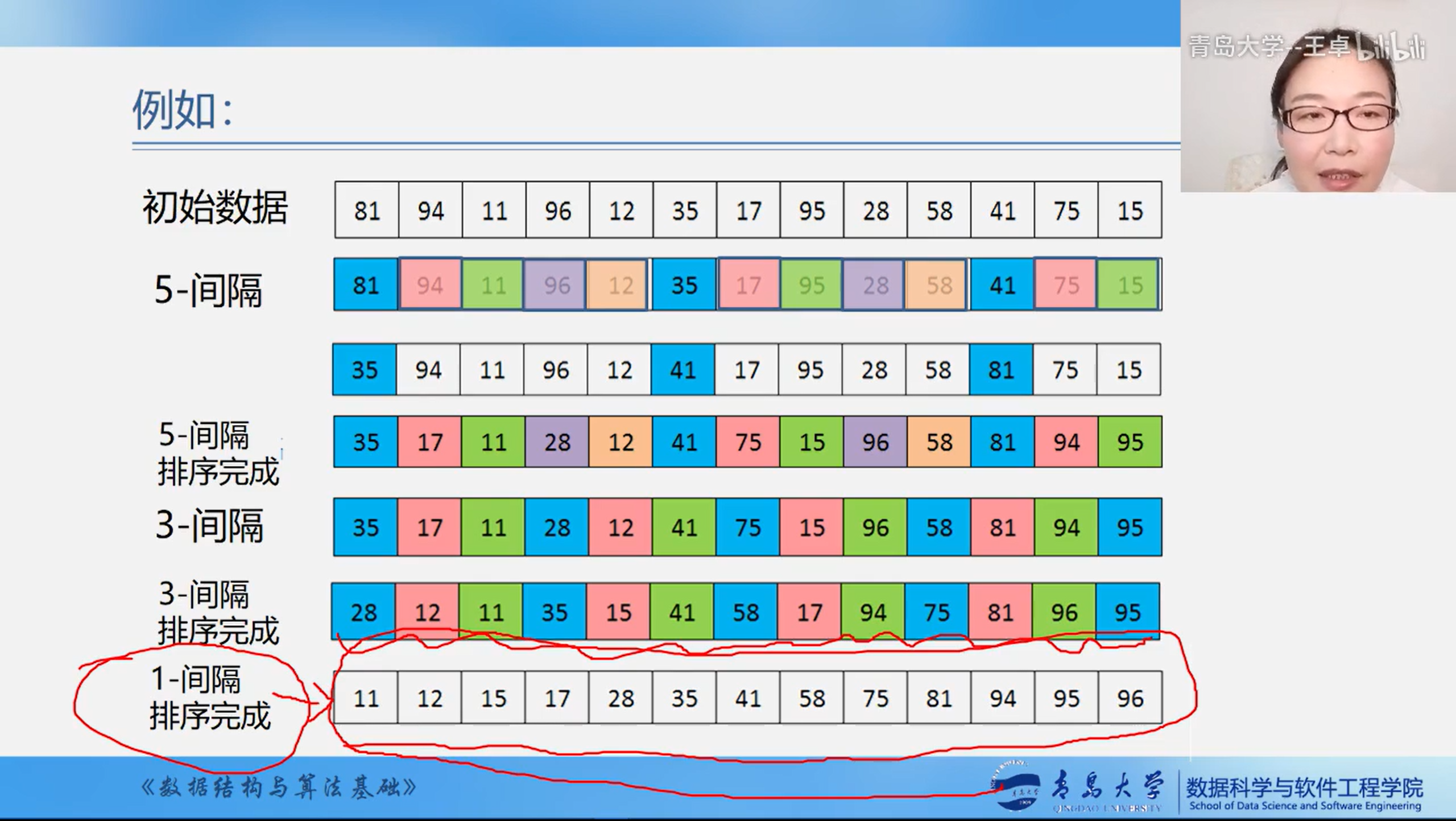
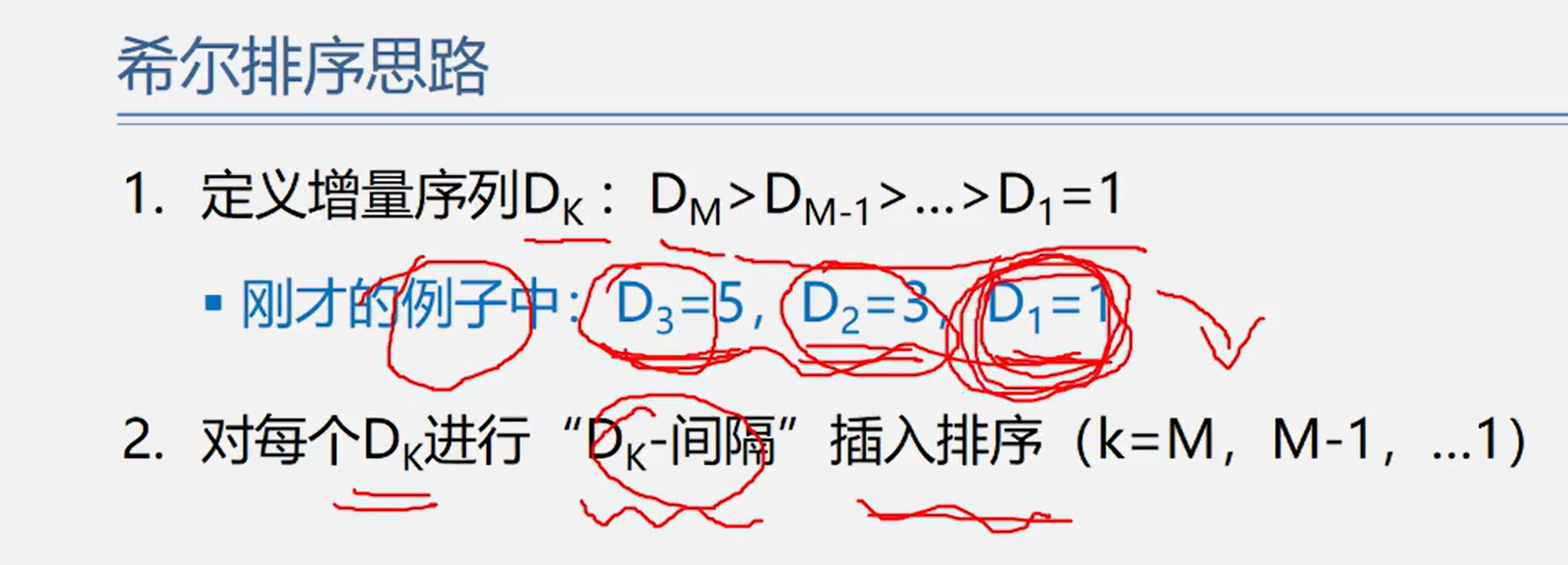
Hill sorting features:
- Once moving, the moving position is large and jumps close to the final position after sorting
- Finally, only a small amount of movement is required in turn
- The increment sequence must be decreasing, and the last one must be 1
- Incremental sequences should be coprime
algorithm
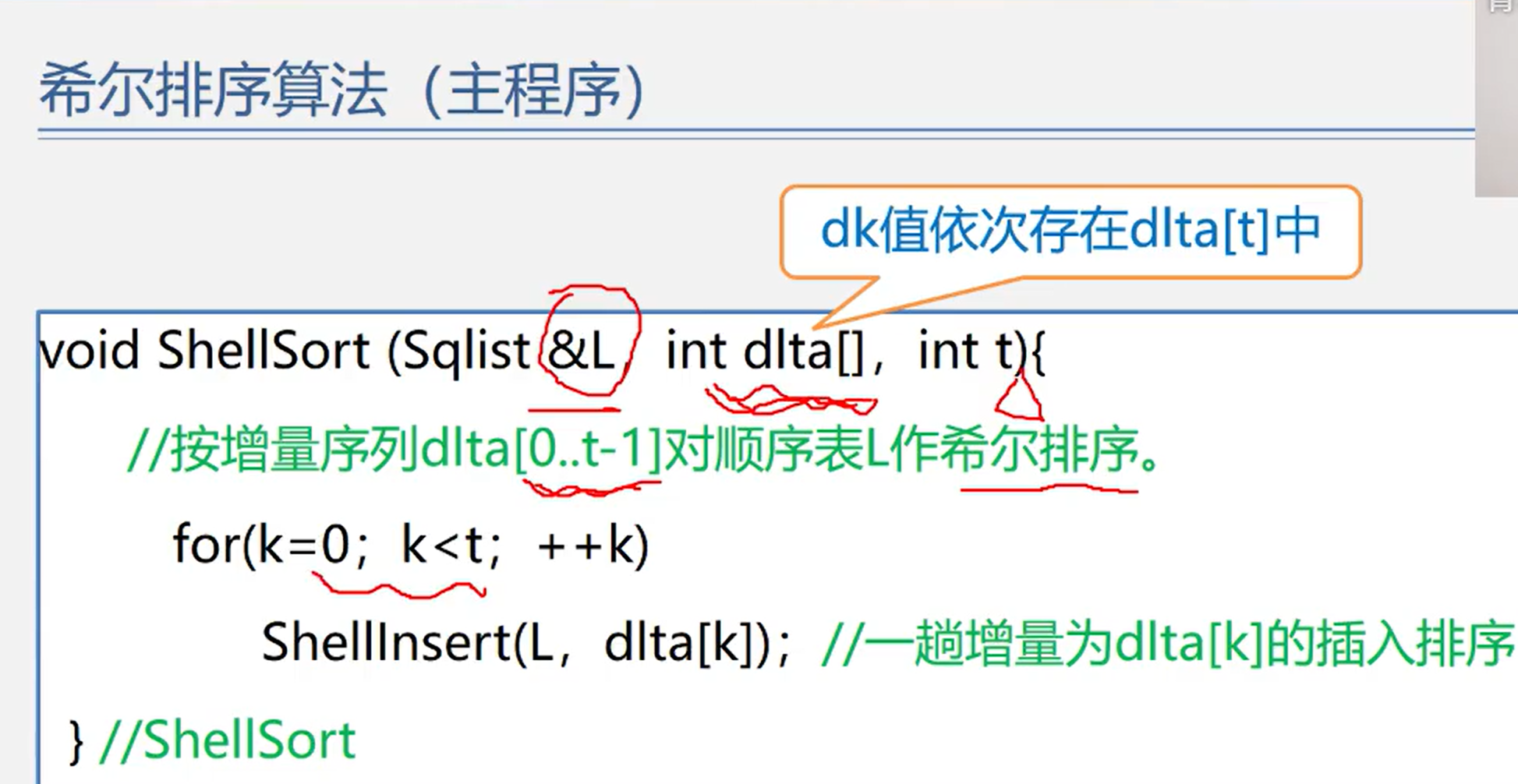
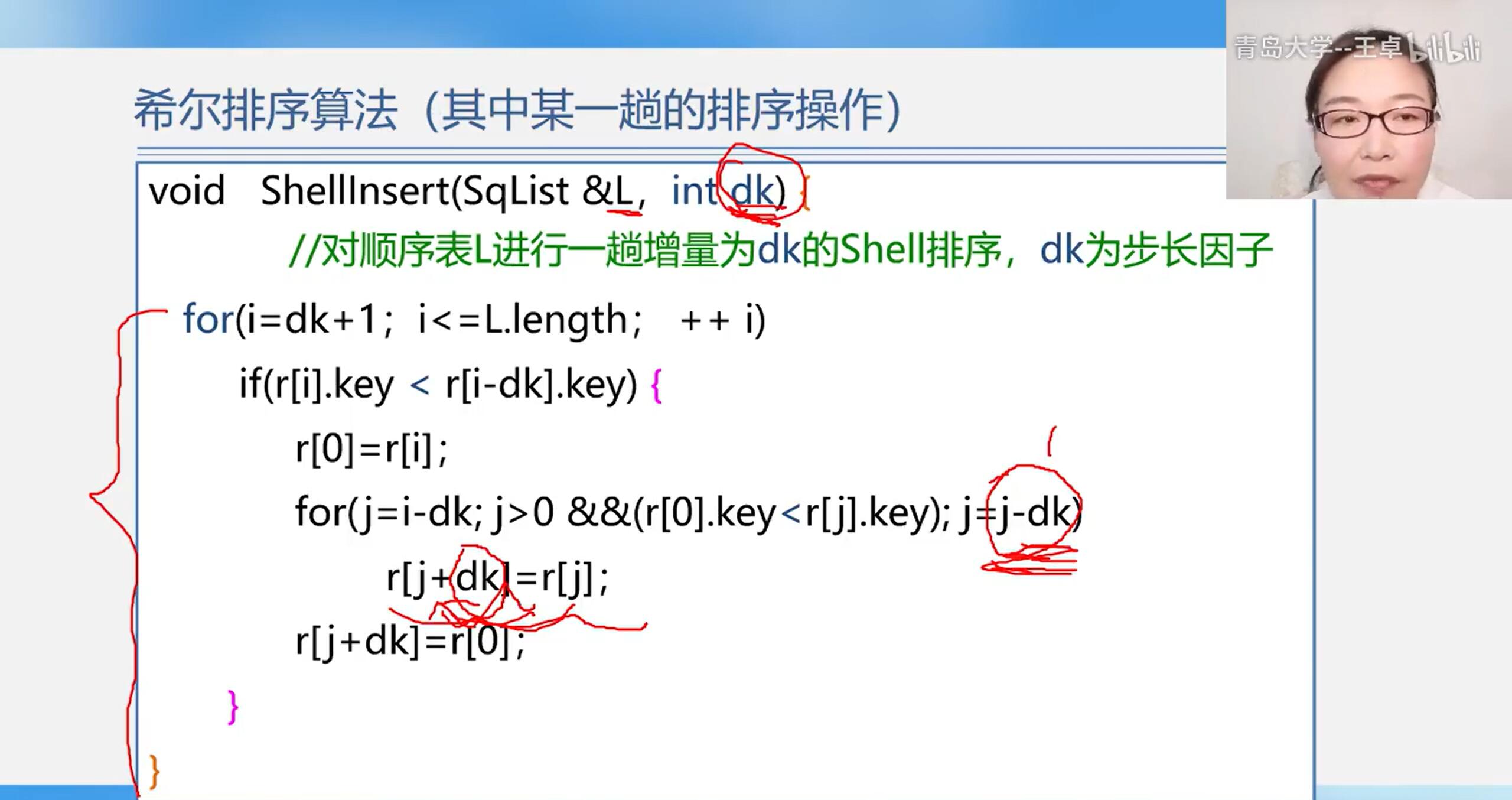
algorithm analysis

Stability of hill sorting algorithm


8.2 exchange sorting
8.2. 1 bubble sort


Summary: n records, n-1 trips in total. The m-th trip needs to be compared n-m times
Algorithm:
void bubble_sort(SqList &L){//Bubble sort algorithm
int m,j,i; RedType x; //Temporary storage during exchange
for(m=1;m<=n-1;m++){//A total of m trips are required
for(j=1;j<=n-m;j++)
if(L.r[j].key>L.r[j+1].key){//Reverse order occurs
x=L.r[j];L.r[j]=L.r[j+1];L.r[j+1]=x;//exchange
}
}
}
Advantages: at the end of each trip, it can not only squeeze out a maximum value to the back position, but also partially straighten out other elements at the same time;
How to improve efficiency?
Once there is no record exchange during a comparison, it indicates that the sorting has been completed, and the algorithm can be ended.
Improved bubble sorting algorithm
void bubble_sort(SqList &L){//Improved bubble sorting algorithm
int m,j,i,flag=1; RedType x; //Flag is used as a flag for whether there is an exchange
for(m=1;m<=n-1 && flag=1;m++){
flag=0;
for(j=1;j<=m;j++)
if(L.r[j].key>L.r[j+1].key){//Reverse order occurs
flag=1;//The flag is 1 in case of exchange. If no exchange occurs, the flag is 0
x=L.r[j];L.r[j]=L.r[j+1];L.r[j+1]=x;//exchange
}
}
}
Evaluation of bubble sorting algorithm
The best time complexity of bubble sorting is O(n)
The worst time complexity of bubble sorting is O(n*n)
The average time complexity of bubble sorting is O(n*n)
An auxiliary space temp is added to the bubble sorting algorithm, and the auxiliary space is S(n)=O(1)
Bubble sorting is stable
Time complexity

8.2. 2 quick sort
-- improved exchange sequencing
Basic idea:
- Take any element (e.g. the first) as the center
- All elements smaller than it are placed in front, and all elements larger than it are placed in back to form the left and right sub tables
- Re select the central element for each sub table and adjust it according to this rule
- Until there is only one element left in each sub table
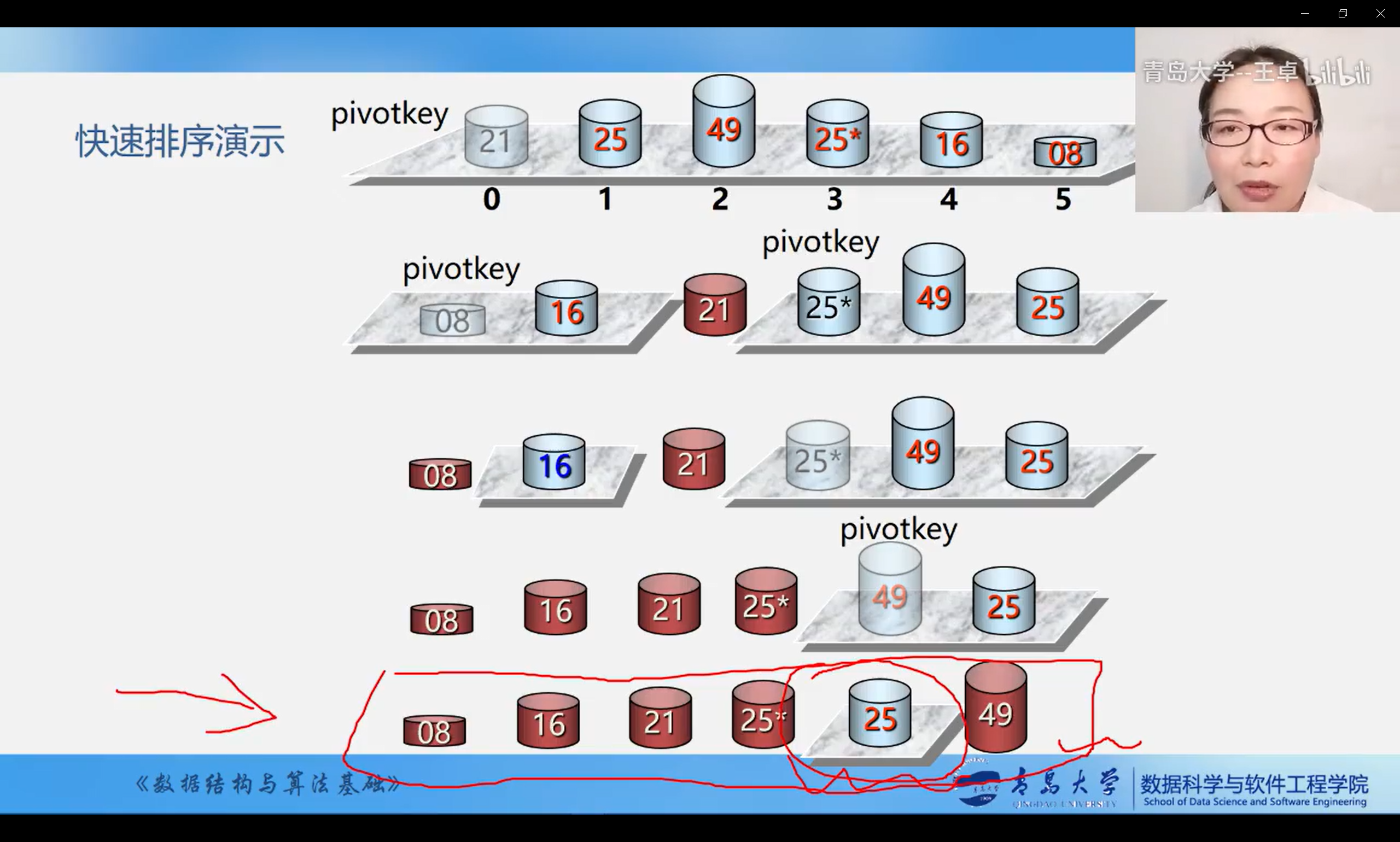
- The sub table of each trip is formed by the alternating approximation method from two ends to the middle
- It is better than that the operations on each sub table in each trip are similar, and recursive algorithm can be used

Algorithm:
void main(){
QSort(L,1,L.length)
}
void QSort(SqList &L,int low, int high){//Quick sort on sequential Table L
if(low<high){ //Length greater than 1
pivotloc = Partition(L,low,high);
//Divide L.r[low....high] into 2, and pivot LOC is the ordered position of the central element
QSort(L,low,pivotloc-1);//Recursively sort low child tables
QSort(L,pivotloc+1,high)//Recursive sorting of high child tables
}
}
int Partition(SqList &L,int low, int high){
L.r[0]=L.r[low]; pivotkey = L.r[low].key
while (low < high){
while(low < high && L.r[high].key>=pivotkey)
--high;
L.r[low] = L.r[high];
while(low<high && L.r[high].key<=pivotkey)
++low;
L.r[low] = L.r[high];
}
L.r[low] = L.r[0];
return low;
}
Analysis of quick sorting algorithm
Time complexity: it can be proved that the average computing time is O(nlog2n)
QSort()😮(nlog2n)
Partition()😮(n)
The experimental results show that in terms of average computing time, quick sorting is the best sorting method in all our discussions.
Spatial complexity: quick sort is not in place
Because the program uses recursion, it needs stack space. In the average case, it needs stack space of O(nlogn), and in the worst case, the stack space can reach O(n)
Stability: quick sort is an unstable sort method
Quick sort is not suitable for sorting originally ordered or basically ordered record sequences.
The selection of partition elements is the key to time performance
The more disordered the input data order, the better the randomness of the selected partition elements and the faster the sorting speed. Quick sorting is not a natural sorting method.
Changing the selection method of partition elements can only change the time performance of the algorithm in the average case, but not in the worst case. That is, in the worst case, the time complexity of quick sort is always O(n*n)
8.3 selection and sorting
8.3. 1 simple selection sort
Basic idea: select the largest (small) element in the data to be sorted and put it in its final position
Basic operation:
- Firstly, through n-1 keyword comparison, find the record with the smallest keyword from n records and exchange it with the first record
- Then, through n-2 keyword comparisons, find the record with the smallest keyword from n-1 records and exchange it with the second record
- Repeat the above process. After sorting for n-1 times, the sorting ends
void selectsort(sqlist &K){
for(i=1;i<L.length;i++){
k=i;
for(j=i+1;j<L.length;j++)
if(L.r[j].key < L.r[k].key)//Record minimum position
k=j;
if(k!=i) L.r[i] <--> L.r[K] //exchange
}
}
Time complexity:
- Record the number of moves
- Best case: 0
- Worst case: 3(n-1)
- Comparison times: the comparison times required for sorting are the same regardless of the status of the sequence to be sorted

Algorithm stability
Simple selection sorting is unstable sorting, which can be changed into stable sorting by modifying the algorithm
8.3. 2 heap sort

It can be seen from the definition of heap that the essence of heap is a complete binary tree satisfying the following properties: any non leaf node in the binary tree is less than (greater than) its child node
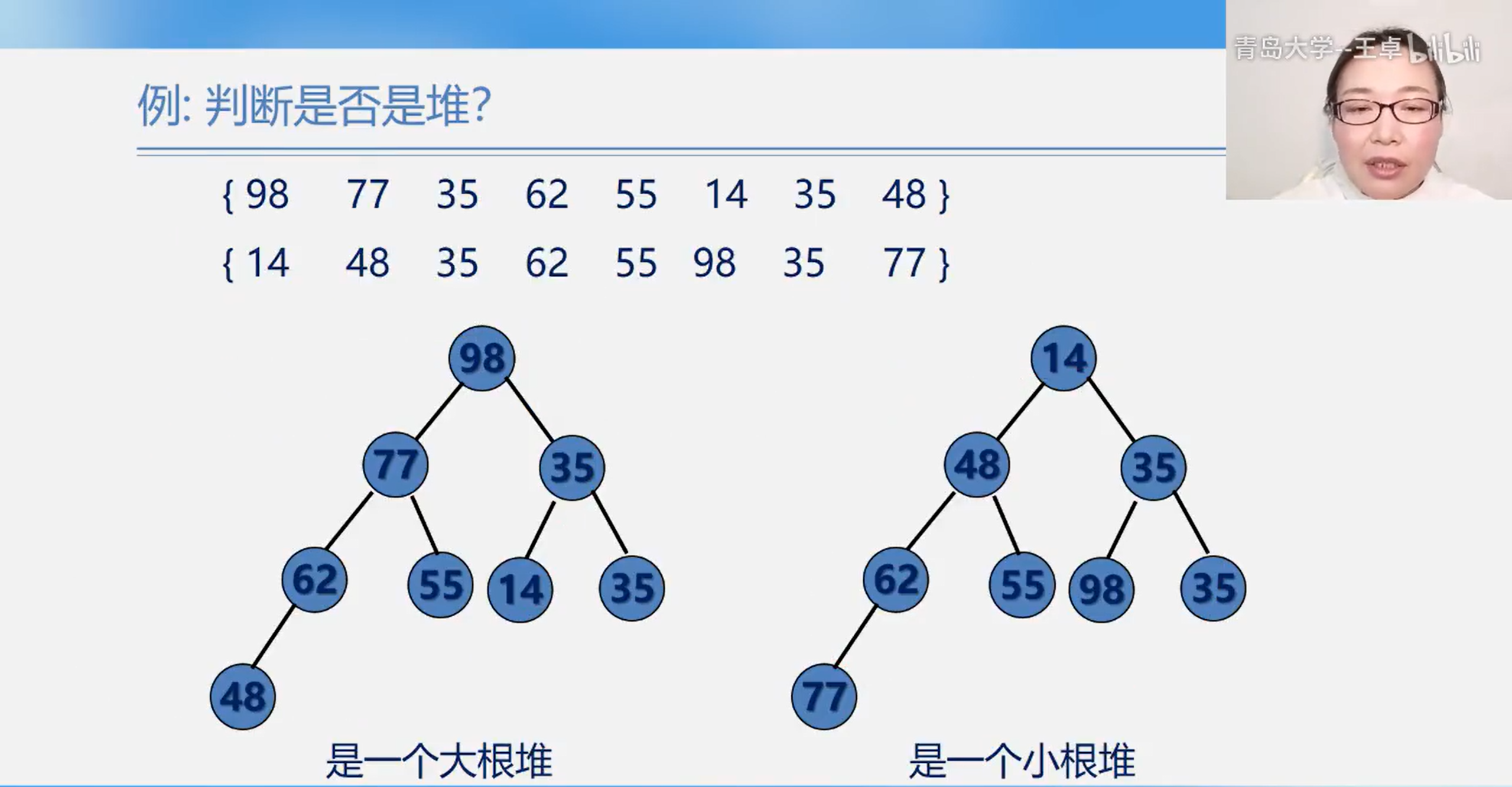
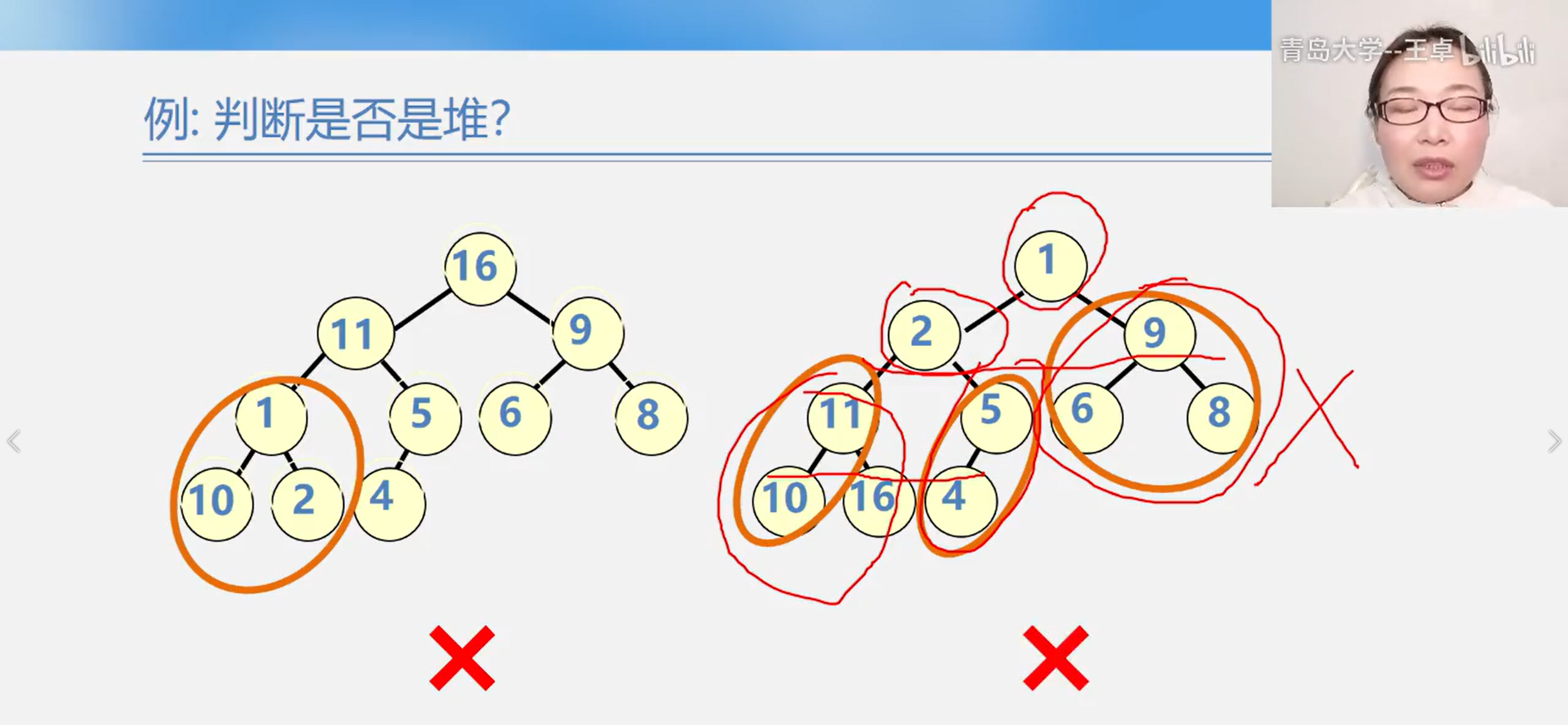
Heap sort
If, after inputting the minimum (maximum) value at the top of the heap, the sequence of the remaining n-1 elements is built into a heap, the sub small value (sub large value) of n elements is obtained... So repeatedly, an ordered sequence can be obtained. This process is called heap sorting
Two problems need to be solved to realize heap sorting:
- How to build a heap from an unordered sequence?
- How to adjust the remaining elements as a new heap after entering the top elements?
Heap adjustment (question 2)
Small root pile:
- After outputting the top element of the heap, replace it with the last element in the heap
- Then compare the root node value with the root node value of the left and right subtrees, and exchange with the smaller one.
- Repeat the above operations until the leaf node, and a new heap will be obtained. This adjustment process from the top of the heap to the leaf is called "filtering"


It can be seen that:
A heap can be obtained by repeatedly "screening" an unordered sequence;
That is, the process of building a heap from an unordered sequence is the process of repeated "screening"
So: how to build a heap from an unordered sequence? (question 1)
obviously:
A single node binary tree is a heap.
In a complete binary tree, all subtrees with leaf nodes (sequence number I > n / 2) as roots are heaps.
In this way, we only need to adjust the subtrees whose nodes are roots with sequence numbers n/2, n/2-1,..., 1 to heap.
That is, corresponding to the unordered sequence composed of n elements, "filtering" only needs to start from the n/2 element

Start with the last non leaf node and adjust accordingly.
- The adjustment starts from the n/2 element and adjusts the binary tree with this element as the root to the heap
- Adjust the binary tree with the node with sequence number n/2-1 as the root to heap
- Adjust the binary tree with the node with sequence number n/2-2 as the root to heap
- Adjust the binary tree with the node with sequence number n/2-3 as the root to heap

In essence, heap sorting is to sort by using the direct internal relationship between parent nodes and child nodes in a complete binary tree
Heap sorting algorithm:
void heapsort(elem R[]){//Heap sort R[1] to R[n]
int i;
for(i= n/2;i>=1;i--)
HeapAdjust(R,i,n);//Build initial reactor
for(i=n;i>1;i--){//Sort n-1 times
Swap(R[1],R[i]);//The root is swapped with the last element
HeapAdjust(R,1,i-1);//Rebuild R[1] to R[n-1]
}
}
Algorithm performance analysis:
The time required for initial stacking shall not exceed O(n)
Sorting phase:
- The time required for sequential re stacking shall not exceed O(logn)
- The time required for n-1 cycles shall not exceed O(nlogn)
T=O(n)+O(nlogn)=O(nlogn)
The time of heap sorting is mainly spent on the repeated screening when building the initial heap and adjusting the new heap. In the worst case, the time complexity of heap sorting is also O(nlog2n), which is the biggest advantage of heap sorting. The heap sort will not be in the "best" or "worst" state regardless of whether the records in the to be sorted sequence are arranged in positive or reverse order.
In addition, heap sorting requires only one record size of auxiliary storage space for exchange.
However, heap sorting is an unstable sorting method. It is not suitable for the case where the number n of records to be sorted is small, but it is still very effective for files with large n.
8.4 merge sort



Algorithm: interested in understanding

8.5 cardinality sorting



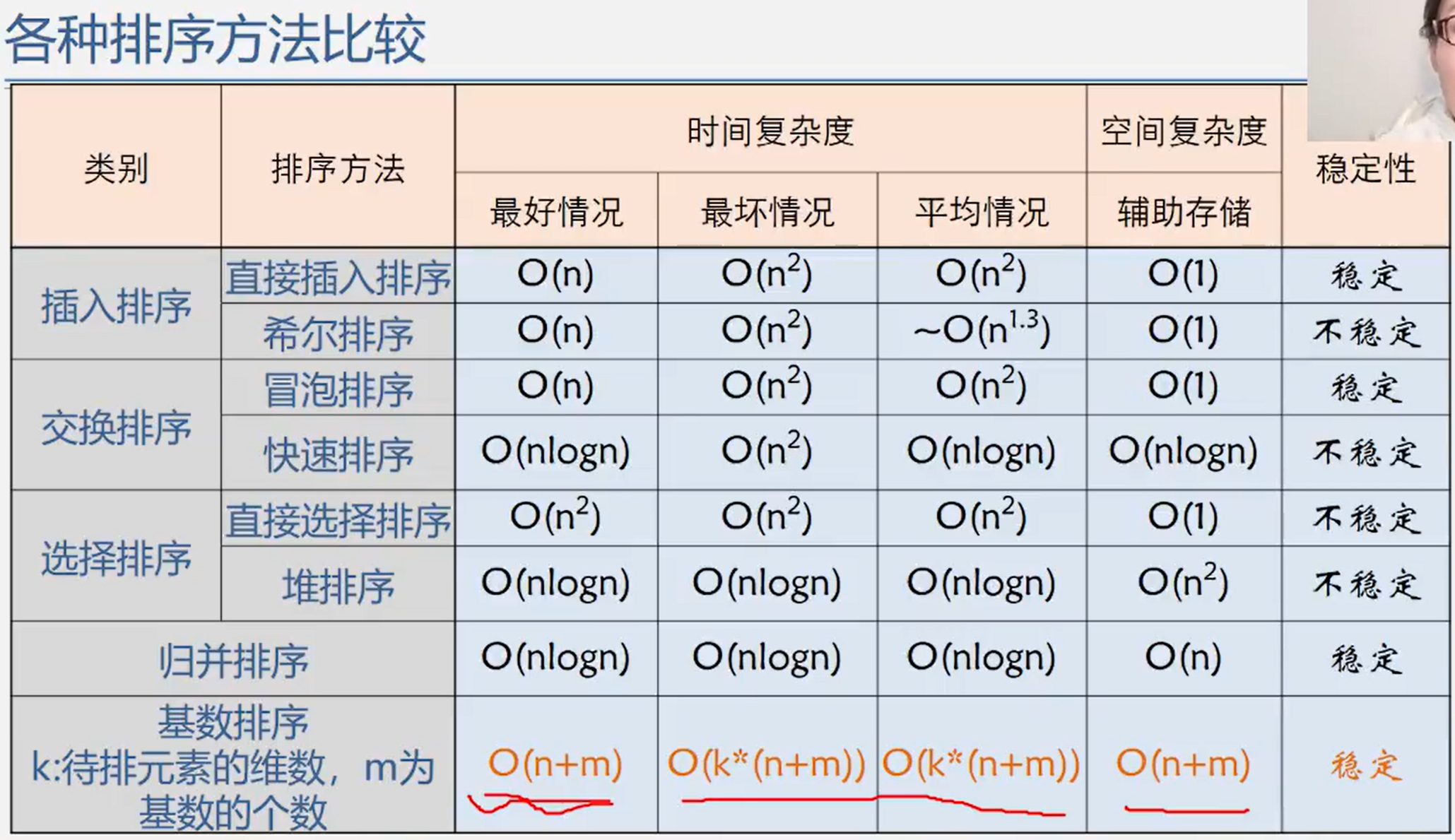
8.6 comparison of various sorting methods


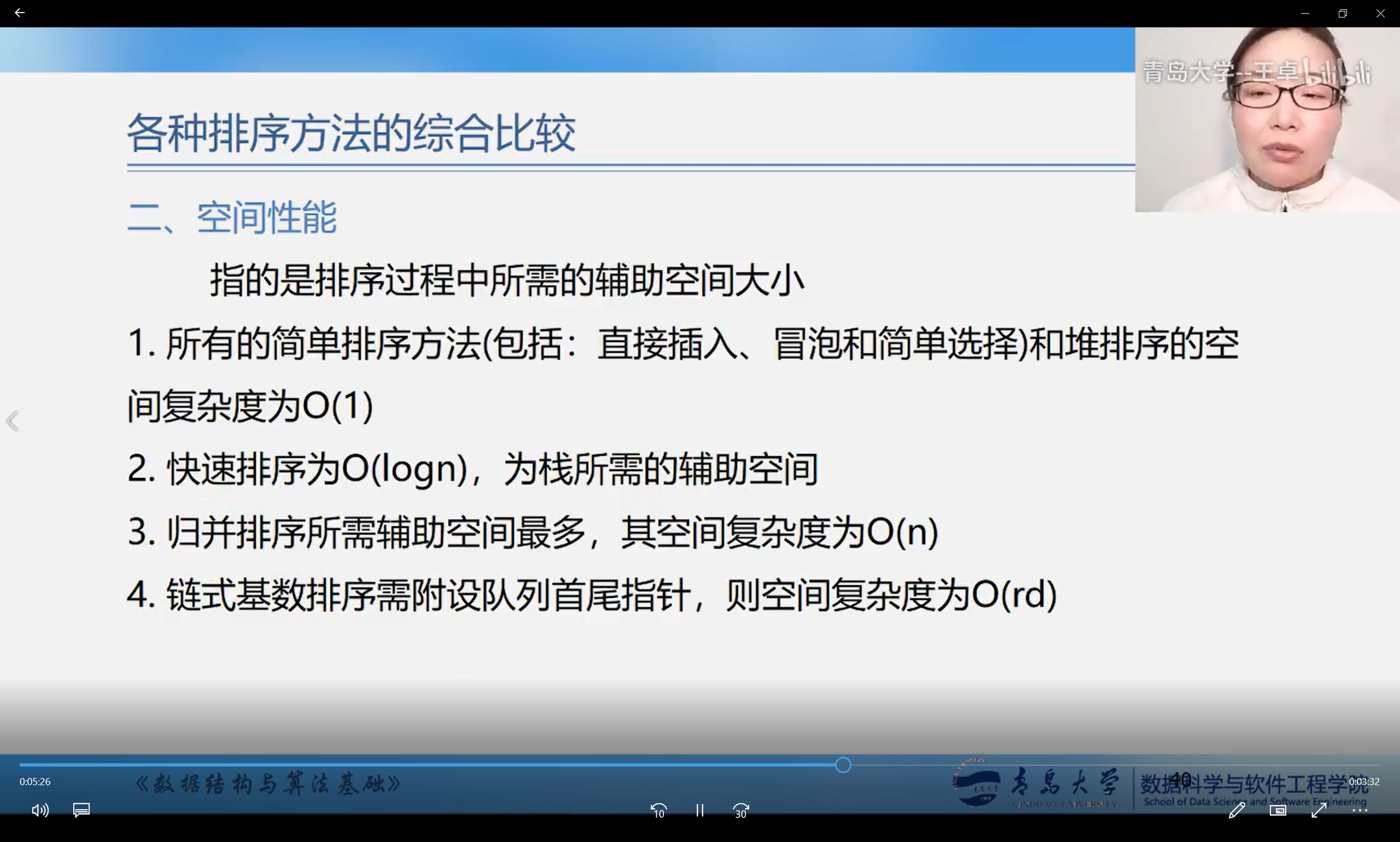

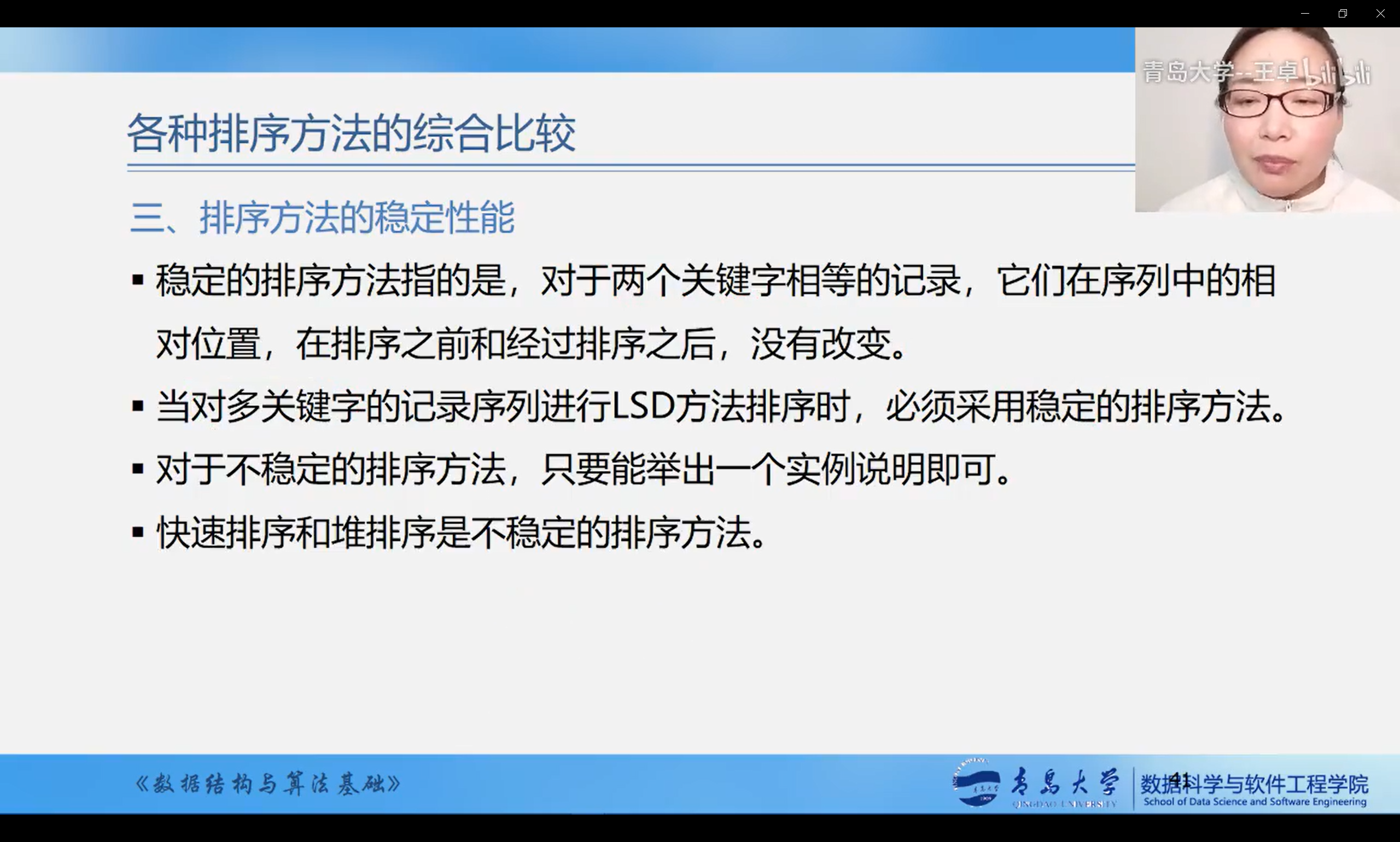
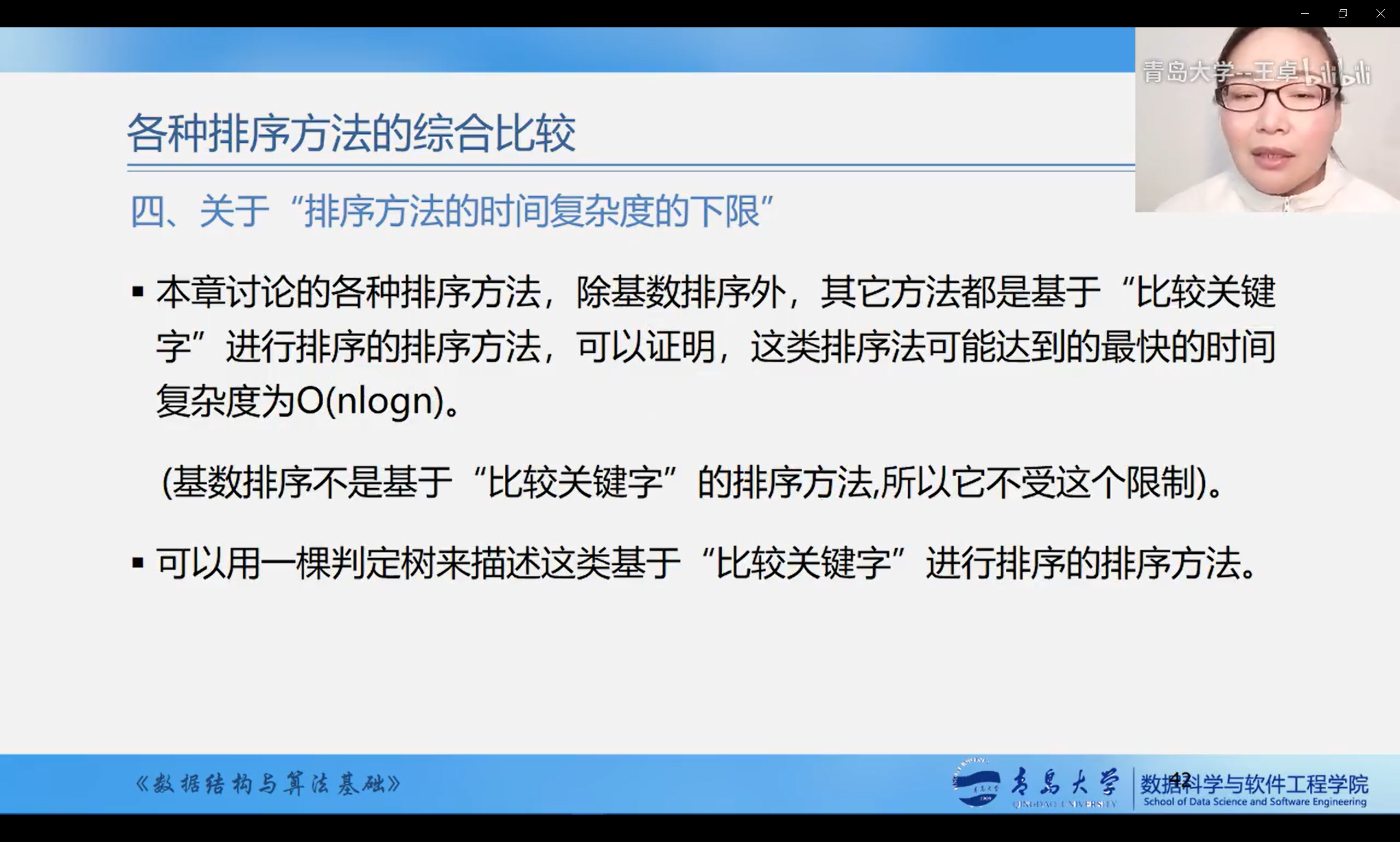
Overall comparison