preface

As one of the nine malignant tumors in primary school, the chicken rabbit cage problem is estimated to be difficult for many people before learning the binary first-order equation. From the perspective of programmers, there are many solutions to the chicken rabbit cage problem, the most common of which are exhaustive method, formula method, etc. today, the method I want to explore is deep learning. It is estimated that I am the first to do so.

Problem introduction

We always ignore some rules we are used to. Imagine, if we don't know that a chicken has two feet and a rabbit has four feet, will the problem of chicken and rabbit in the same cage be so easy?

The essence of deep learning is to find a general logical algorithm between limited data and results. This algorithm is generally called experience in life. Therefore, this paper takes the problem of chicken and rabbit in the same cage as an example. Given the data and results, let the computer find the general rules (chicken has two feet and rabbit has four feet).

It is worth noting that we should not presume to use the existing rules to explain or repair the neuron connection weight and threshold, otherwise it will only backfire.

First attempt (failure experience)

Since this rule is too simple, I intend to adopt the simplest structure of one input layer, one hidden layer and one output layer for neural network. The physical structure is as follows:

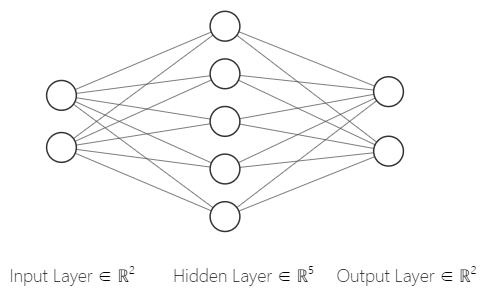
It seems a bit wasteful to use tensorflow for such a simple neural network structure, so I first used Excel table for simulation, as shown in the following figure:

By constantly replacing the weight value and threshold value (made by macro), after 301 iterations, the loss function (error square) curve is as follows:

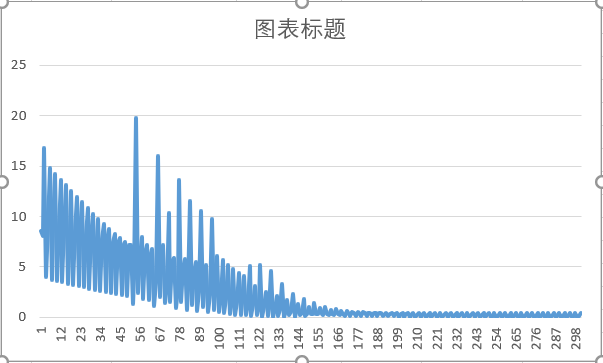
Because only one set of data is used in back propagation, the jitter of loss function curve is understandable. Although the image intuitively shows the learning process, it is a pity that the final network fails to converge, and the actual prediction also has large errors. The reason may be that the data is not enough (only three groups of data are given), or the number of neurons in the hidden layer is small.

Second experiment

I learned the lesson from the first time. This time, I plan to complete the experiment with python+tensorflow.

Experimental environment

• python3.6
• tensorflow2.5

Physical structure of neural network

It is also a three-layer structure, but the number of neurons in the hidden layer becomes 10.

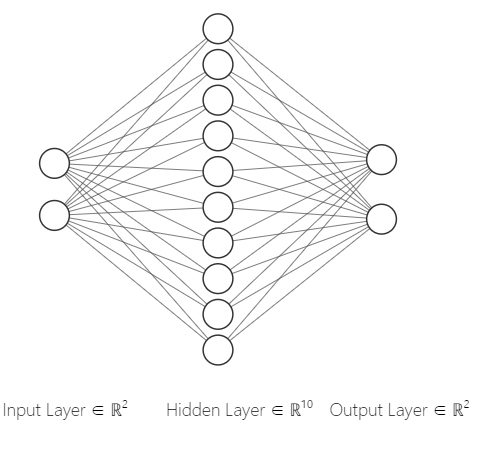
Prepare data

Deep learning is most dependent on data, so data preparation is the first step to start deep learning. This paper has prepared 10 groups of data, and you can add more data as needed.

def train_data():
    x = [[2, 6], [3, 8], [3, 10], [4, 10], [4, 12], [4, 14], [5, 12], [5, 14], [5, 16], [5, 18]]
    x = np.array(x)

    y = [[1, 1], [2, 1], [1, 2], [3, 1], [2, 2], [1, 3], [4, 1], [3, 2], [2, 3], [1, 4]]
    y = np.array(y)
    return (x, y)

x_train = train_data()[0]
y_train = train_data()[1]

Build neural network

# Neural network structure: 2 neurons in input layer, 10 neurons in hidden layer and 2 neurons in output layer
model = keras.Sequential(
    [keras.layers.Flatten(input_shape=(2,)),
     keras.layers.Dense(10, activation='relu'),
     keras.layers.Dense(2)])

Define optimization method

# Define loss function and optimization algorithm
model.compile(optimizer=keras.optimizers.Adam(0.001), loss='mse', metrics=['accuracy'])

Model training and preservation

# The model training is verified every 20 times, with a total of 5000 times
model.fit(x_train, y_train, epochs=5000, validation_data=val_data(), validation_freq=100)

# Save model
model.save("model.h5")

Among them, the verification set comes from the training set, and the number is only reduced.

def val_data():
    x = [[2, 6], [3, 8], [4, 10], [4, 12], [4, 14], [5, 14], [5, 18]]
    y = [[1, 1], [2, 1], [3, 1], [2, 2], [1, 3], [3, 2], [1, 4]]
    x = np.array(x)
    y = np.array(y)
    return (x, y)

The training effect is as follows:

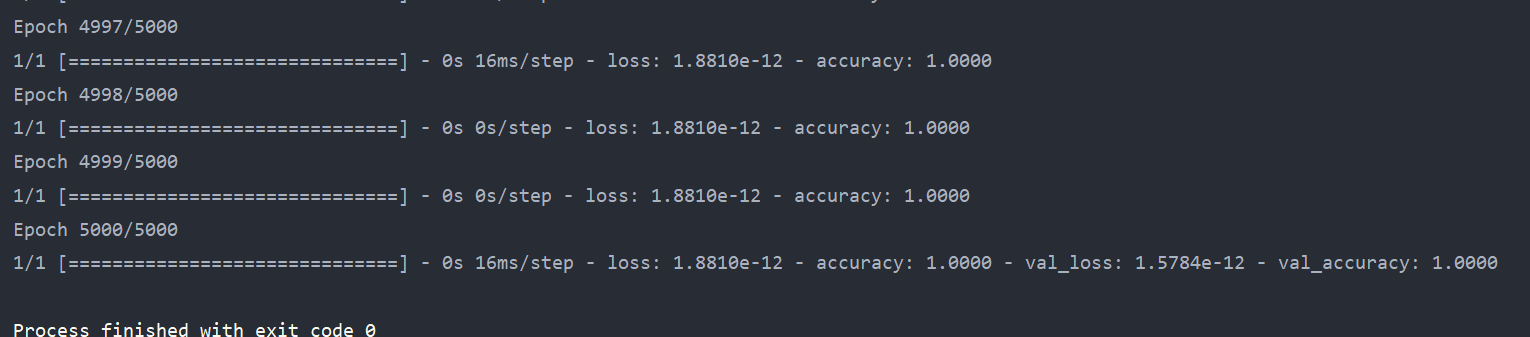
Model test

After training the model, it naturally needs to be tested, and the data used in the test does not appear in the training set. Test related codes are as follows.

from tensorflow import keras
import numpy as np


# Test data
def test_data():
    x = [[6, 14], [6, 16], [6, 18], [6, 20], [6, 22]]
    y = [[5, 1], [4, 2], [3, 3], [2, 4], [1, 5]]
    return (np.array(x), np.array(y))


# Prepare data
x_test = test_data()[0]
y_test = test_data()[1]

# Loading model
network = keras.models.load_model("model.h5")

# Get results
y_predict = network.predict(x_test)
print(y_predict)

The output results are shown in the figure below:

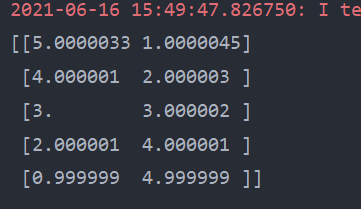
As you can see, the final result is very close to the data of label y.

Application results

The model has passed the test. Now apply the model to practical use.

from tensorflow import keras
import numpy as np
import ast

# Loading model
network = keras.models.load_model("model.h5")

# Encapsulate data
data = ast.literal_eval(input("Please enter the number of heads and feet:"))
data = [data]
data = np.array(data)

# Get results
y_predict = network.predict(data)
print("Chicken has" + str(round(y_predict[0][0])) + "only,Rabbit has" + str(round(y_predict[0][1])) + "Only.")

The final measured effect is shown in the figure below:

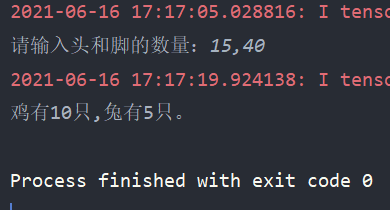
So far, the problem of chicken and rabbit in the same cage is solved by deep learning.

appendix

ANN.py

from tensorflow import keras
import numpy as np
import tensorflow as tf


def train_data():
    x = [[2, 6], [3, 8], [3, 10], [4, 10], [4, 12], [4, 14], [5, 12], [5, 14], [5, 16], [5, 18]]
    x = np.array(x)

    y = [[1, 1], [2, 1], [1, 2], [3, 1], [2, 2], [1, 3], [4, 1], [3, 2], [2, 3], [1, 4]]
    y = np.array(y)
    return (x, y)


def val_data():
    x = [[2, 6], [3, 8], [4, 10], [4, 12], [4, 14], [5, 14], [5, 18]]
    y = [[1, 1], [2, 1], [3, 1], [2, 2], [1, 3], [3, 2], [1, 4]]
    x = np.array(x)
    y = np.array(y)
    return (x, y)


# def test_data():
#     x = [[6, 14], [6, 16], [6, 18], [6, 20], [6, 22]]
#     y = [[5, 1], [4, 2], [3, 3], [2, 4], [1, 5]]
#     return (x, y)


# Step 1: import api
# 1.import tensorflow as tf
# #The second step is to segment the data set into training set and test set
# 2.train,test
# #The third step is to build an appropriate network model (forward propagation process)
# 3.model=tf.keras.models.Sequential
# #The fourth step is to configure the training method, select the training optimizer and select the loss function
# 4.model.compile
# #Step 5 execute the training process in fit
# 5.model.fit()
# #Step 6: output parameters of training results
# 6.model.summary

x_train = train_data()[0]
y_train = train_data()[1]

# Neural network structure: 2 neurons in input layer, 10 neurons in hidden layer and 2 neurons in output layer
model = keras.Sequential(
    [keras.layers.Flatten(input_shape=(2,)),
     keras.layers.Dense(10, activation='relu'),
     keras.layers.Dense(2)])

# Define loss function and optimization algorithm
model.compile(optimizer=keras.optimizers.Adam(0.001), loss='mse', metrics=['accuracy'])

# The model training is verified every 20 times, with a total of 1000 times
model.fit(x_train, y_train, epochs=5000, validation_data=val_data(), validation_freq=100)

# Save model
model.save("model.h5")

test.py

from tensorflow import keras
import numpy as np


# Test data
def test_data():
    x = [[6, 14], [6, 16], [6, 18], [6, 20], [6, 22]]
    y = [[5, 1], [4, 2], [3, 3], [2, 4], [1, 5]]
    return (np.array(x), np.array(y))


# Prepare data
x_test = test_data()[0]
y_test = test_data()[1]

# Loading model
network = keras.models.load_model("model.h5")

# Get results
y_predict = network.predict(x_test)
print(y_predict)

prediction.py

from tensorflow import keras
import numpy as np
import ast

# Loading model
network = keras.models.load_model("model.h5")

# Encapsulate data
data = ast.literal_eval(input("Please enter the number of heads and feet:"))
data = [data]
data = np.array(data)

# Get results
y_predict = network.predict(data)
print("Chicken has" + str(round(y_predict[0][0])) + "only,Rabbit has" + str(round(y_predict[0][1])) + "Only.")