Principle introduction
Chow algorithm allocates bits according to the channel capacity of each subchannel. Its optimization criterion is to maximize the system margin on the premise of maintaining the target bit error rate. The algorithm allocates bits step by step through the iterative process, and gradually increases the margin of the system until all bits are allocated.
Bit allocation
(1) Calculate the signal-to-noise ratio of each subchannel,
S
N
R
(
i
)
,
∀
i
SNR\left( i \right),\forall i
SNR(i), ∀ i, assuming that the signal energy on all subchannels is normalized,
ε
(
i
)
=
1
,
∀
i
\varepsilon \left( i \right)=1,\forall i
ε(i)=1,∀i
(2) Order
γ
m
arg
i
n
=
0
dB
{{\gamma }_{m\arg in}}=0\text{dB}
γ margin = 0dB, the number of iterations is
I
t
e
r
c
o
u
n
t
=
0
Itercount=0
Itercount=0, the number of subchannels used is
U
s
e
d
c
a
r
r
i
e
r
s
=
N
Usedcarriers=N
Usedcarriers=N, where
N
N
N is the maximum number of available subchannels
(3) Sequential calculation
b
(
i
)
b(i)
b(i) ,
b
^
(
i
)
\hat{b}(i)
b^(i) ,
d
i
f
f
(
i
)
diff(i)
diff(i) and
U
s
e
d
c
a
r
r
i
e
r
s
Usedcarriers
Usedcarriers
b
(
i
)
=
log
2
(
1
+
S
N
R
(
i
)
Γ
+
γ
m
arg
i
n
(
d
B
)
)
b(i)={{\log }_{2}}\left( 1+\frac{SNR(i)}{\Gamma +{{\gamma }_{m\arg in}}(dB)} \right)
b(i)=log2(1+Γ+γmargin(dB)SNR(i))
b
^
(
i
)
=
r
o
u
n
d
(
b
(
i
)
)
\hat{b}(i)=round(b(i))
b^(i)=round(b(i))
d
i
f
f
(
i
)
=
b
(
i
)
−
b
^
(
i
)
diff(i)=b(i)-\hat{b}(i)
diff(i)=b(i)−b^(i)
if
b
^
(
i
)
=
0
\hat{b}(i)\text{=}0
b^(i)=0,
U
s
e
d
c
a
r
r
i
e
r
s
=
N
−
1
Usedcarriers\text{=}N-1
Usedcarriers=N−1,
Γ
\Gamma
Γ by
S
N
R
SNR
SNR spacing is defined as the ideal distance when the system reaches the transmission capacity C
S
N
R
SNR
SNR and actual transmission capacity
R
R
R
S
N
R
SNR
SNR ratio.
Γ
\Gamma
Γ yes
B
E
R
BER
As a function of BER and channel coding mode, assuming QAM modulation, then
Γ
=
−
ln
(
5
B
E
R
t
arg
e
t
)
1.5
\Gamma \text{=}\frac{-\ln \left( 5BE{{R}_{t\arg et}} \right)}{1.5}
Γ=1.5−ln(5BERtarget)
(4) Calculate
R
=
s
u
m
(
{
b
^
(
i
)
}
)
R\text{=}sum\left( \left\{ \hat{b}\left( i \right) \right\} \right)
R=sum({b^(i)}), if
R
=
0
R=0
If R=0, the channel is too poor to be used
(5) Calculate
γ
m
a
r
g
i
n
{{\gamma }_{margin}}
γmargin
γ
m
a
r
g
i
n
=
γ
m
a
r
g
i
n
+
10
log
10
(
2
R
−
R
T
U
S
e
d
C
a
r
r
i
e
r
s
)
{{\gamma }_{margin\text{ }}}={{\gamma }_{margin}}+10{{\log }_{10}}\left( {{2}^{\frac{R-{{R}_{T}}}{USedCarriers}}} \right)
γmargin =γmargin+10log10(2USedCarriersR−RT)
(6) Number of iterations
I
t
e
r
c
o
u
n
t
=
I
t
e
r
c
o
u
n
t
+
1
Itercount=Itercount+1
Itercount=Itercount+1
(7) If
R
≠
R
T
R\ne {{R}_{T}}
R = RT , and
I
t
e
r
c
o
u
n
t
<
M
a
x
c
o
u
n
t
Itercount<Maxcount
Itercount < maxcount, make
U
s
e
d
c
a
r
r
i
e
r
s
=
N
Usedcarriers=N
Usedcarriers=N, go to step (3), otherwise go to step (8)
(8) If
R
>
R
T
R>{{R}_{T}}
R> RT, find the smallest
d
i
f
f
(
i
)
diff\left( i \right)
diff(i), correspondingly
b
^
(
i
)
=
b
^
(
i
)
-
1
\hat{b}(i)\text{=}\hat{b}(i)\text{-}1
b^(i)=b^(i)-1,
d
i
f
f
(
i
)
=
d
i
f
f
(
i
)
+
1
diff\left( i \right)=diff\left( i \right)+1
diff(i)=diff(i)+1, repeat this step until
R
=
R
T
R\text{=}{{R}_{T}}
R=RT
(9) If
R
<
R
T
R<{{R}_{T}}
R < RT, find the largest
d
i
f
f
(
i
)
diff\left( i \right)
diff(i), correspondingly
b
^
(
i
)
=
b
^
(
i
)
+
1
\hat{b}(i)\text{=}\hat{b}(i)\text{+}1
b^(i)=b^(i)+1 ,
d
i
f
f
(
i
)
=
d
i
f
f
(
i
)
-
1
diff\left( i \right)=diff\left( i \right)\text{-}1
diff(i)=diff(i)-1, repeat this step until
R
=
R
T
R\text{=}{{R}_{T}}
R=RT
(10) The transmission power on each subchannel is adjusted so that it corresponds to
b
(
i
)
b(i)
b(i)
P
e
(
i
)
=
P
e
,
t
arg
e
t
,
∀
i
{{P}_{e}}\left( i \right)={{P}_{e,t\arg et}},\ \forall i
Pe(i)=Pe,target, ∀i
(11) Adjust the total transmit power. Multiply all used subchannels by the same scale factor,
Total signal power
P
=
P
T
P={{P}_{T}}
P=PT
Simulation parameter setting
| Parameter name | Parameter value |
|---|---|
| Average signal-to-noise ratio | 20 |
| Bit error rate | 1 0 − 4 10^{-4} 10−4 |
| Number of subcarriers | 32 |
| Average transmit power | 1 |
| Upper limit of total number of bits | 128 |
The experimental results are as follows
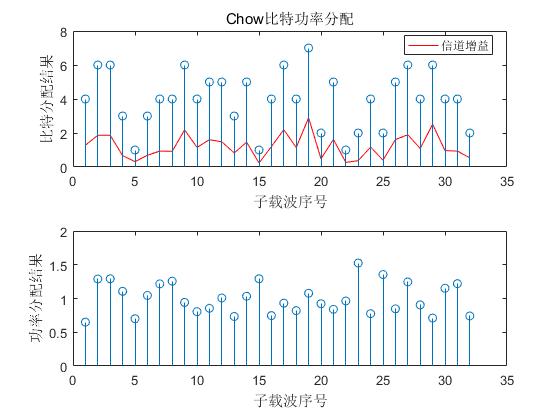
As can be seen from the above figure, the final number of bits of the system is maximized by gradually adjusting the allocated bits. At the same time, it can also be seen that the result of Chow algorithm allocation has certain advantages. It discards the subcarriers with poor channel conditions, that is, the subcarriers used by the system for final transmission must have information transmission, which may be confirmed by the simulation results.
The code is as follows:
Main function
clear ;
close all;
clc;
N_subc=32;
BER=1e-4;
gap=-log(5*BER)/1.5;
P_av=1;
Pt=P_av*N_subc;
SNR_av=20;
noise=P_av./10.^(SNR_av./10);
Rt=128;
subcar_gains=random('rayleigh',1,1,N_subc);
SNR=(subcar_gains.^2)./(noise*gap);
[bit_alloc,power_alloc,Iterate_count]=Chow(SNR,N_subc,gap,Rt);
power_alloc=Pt.*(power_alloc./sum(power_alloc));
figure(1);
subplot(2,1,1);
plot(subcar_gains,'-r');
legend('Channel gain');
hold on;
stem(bit_alloc);
title('Chow Bit power allocation');
ylabel('Bit allocation result');
xlabel('Subcarrier serial number');
subplot(2,1,2);
stem(power_alloc);
ylabel('Power allocation results');
xlabel('Subcarrier serial number');
Chow.m
function [bits_alloc, power_alloc,iter_count] = Chow(SNR,N_subc,gap,Rt)
% ---------------------initialization-------------------------
margin=0; %Initialization threshold
Max_count=10; %Maximum number of iterations
iter_count=0; %Initialization iteration
total_bits=0; %Always more special than
power_alloc=zeros(1,N_subc); %Initialization power allocation result
bits_alloc=zeros(1,N_subc); %Initialization bit allocation result
temp_bits=zeros(1,N_subc); %Initialize intermediate variable
bit_round=zeros(1,N_subc); %Initialize rounding bit
diff=zeros(1,N_subc); %Initialize differential bit
%-----------------------------bits allocation-------------------------
while (total_bits~=Rt)&&(iter_count<Max_count)
iter_count=iter_count+1;
N_use=N_subc; %Number of available subcarriers during initialization
temp_bits=log2(1+SNR./(1+margin/gap)); %Initial result of bit allocation
bit_round=round(temp_bits); %Number of bits after rounding
diff=temp_bits-bit_round; %Bit difference
total_bits=sum(bit_round); %Total number of bits after rounding
if(total_bits==0)
disp('the channel is not be used'); %The channel is too poor to use
end
N_notuse=length(find(bit_round==0)); %Number of unused subcarriers
N_use=N_subc-N_notuse; %Number of subcarriers used
margin=margin+10*log10(2^((total_bits-Rt)/N_use)); %Update threshold
end
%------------------------------bits alteration--------------------------
while(total_bits>Rt) %If bit_total>Rt,Find the smallest bit_diff(i)
use_ind=find(bit_round>0); %Accordingly bit_round Minus 1, bit_total=bit_total-1
bit_diff=diff(use_ind); %bit_diff(i)Add 1 until bit_total=Rt
id=find(bit_diff==min(bit_diff),1);
ind_alter=use_ind(id);
bit_round(ind_alter)=bit_round(ind_alter)-1;
diff(ind_alter)=diff(ind_alter)+1;
total_bits=sum(bit_round);
end
while(total_bits<Rt) %If bit_total<Rt,Find the largest bit_diff(i)
use_ind=find(bit_round~=0); %Accordingly bit_round Plus 1, bit_total=bit_total+1
bit_diff=diff(use_ind); %bit_diff(i)Minus 1 until bit_total=Rt
id=find(bit_diff==max(bit_diff),1);
ind_alter=use_ind(id);
bit_round(ind_alter)=bit_round(ind_alter)+1;
diff(ind_alter)=diff(ind_alter)-1;
total_bits=sum(bit_round);
end
bits_alloc=bit_round;
%--------------------------power allocation-----------------------------
power_alloc=(2.^bits_alloc-1)./SNR;
end