Circular linked list

One. Establishment of linked list
The tail node pointer field of the linked list is NULL For the establishment of circular linked list, the tail node refers to the head node

void CreatByRear(LinkList head)
{
   Node*r,*s;
   char name[20];
   int number;
   r=head;
   printf("Please enter the student's name and student number:\n");
   while(1)
   {
   scanf("%s",name);
   scanf("%d",&number);
   if(number==0)
      break;
    s=(Node*)malloc(sizeof(Node));
    strcpy(s->name,name);
    s->number=number;
    r->next=s;
    r=s;
   }
   r->next=head;

Judgment of the end of the linked list
To judge whether a node is the end of the table, the single linked list only needs to judge whether the pointer field of the node is null (P - > next = = null). If yes, it is the end node, otherwise it is not. If the circular linked list judges whether it is the end node, it is to judge whether the pointer field of the node points to the head of the linked list (P - > next = head).
Well, after reading the introduction of the above circular linked list, do you think it is very simple? Now let's prepare for the actual combat simulation.
Before the simulation, let's give you a question to think about.
Question: there are n children. Make a circle according to the number of 1, 2,..., N. start counting from the first and report to the exit of m. start from the next and continue counting from the first and report the exit of m. repeat this process. Finally, send a prize to the remaining child, write a program and output the serial number of the child who won the prize.
For friends who haven't contacted the linked list, it is estimated that they will choose to use arrays to solve this problem. Since they all mentioned this, let's talk about its solution
1, Array
Use an array to store the n numbers,

arr[6]={1,2,3,4,5,6}

Then keep traversing. For the selected number, we make a mark. For example, if the number arr[2]=3 is selected, we can make a mark. For example, let arr[2]=-1 to indicate that the number stored in arr[2] has been out.

arr  1 2 3 4 5 6
         .
         .The first one out
         .
     1 2 -1 4 5 6

Then, according to this method, keep traversing the array and marking, and know that only one element in the array is non-1.
I don't think the idea is very simple, but the coding process is still very challenging.
Note that the time complexity of this approach is O(n*m) and the space complexity is O(n);
Here is the core code.

int cnt=0,i=0,k=0;
while(cnt!=n) //Because it requires the out order of n individuals, cnt needs to cycle continuously to reach n
{
   i++;
   if(i>n)
     i=1;
   if(a[i]==0)
  {
    k++;
    if(k==m)
      {
      a[i]=1;
      cnt++;
      printf("%d",i);
      k=0;
      }
   }
}

OK, after the above introduction, do you have a good understanding of Joseph Ring? Now let's use circular linked list to solve this problem.
Structure code:

typedef struct node
{
   int data;
   struct node*next;
 }

I believe that the creation of linked list should be able to, and I have written the creation process of circular linked list above, so I will go directly to the core code below

while(p->next!=p)//If P - > next = P, there is only one element
{
    for(int i=1;i<m;i++)
    {
       r=p;//Keep the previous code out
       p=p->next;
     }
     printf("%d",p->data);
     r->next=p->next;
     p=p->next;
 }

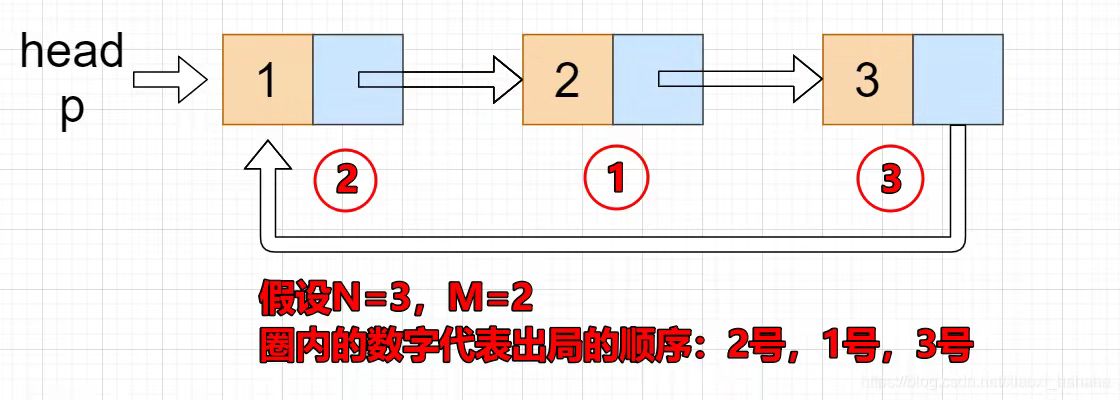
Here is the complete code

#include<bits/stdc++.h>
using namespace std;
//Joseph Ring problem with linked list (circular linked list) 
 
typedef struct node  //typedef is used to rename the data type struct node and name it Node 
{
 int data;
 struct node* next;
}Node;
 
void ysflb(int N,int M)  //There are N people in total, and the one with check-in number M is out 
{
 //Initialize circular linked list
 Node *head = NULL,*p=NULL,*r=NULL;   //Head is the head pointer, pointing to the first node of the linked list. At the beginning, it is assigned NULL, which means it does not point to any node 
 head = (Node*)malloc(sizeof(Node));  //Let the head point to an actual space
 if(NULL==head)  //The memory space application may fail. In most cases, the application will not fail 
 {
   cout<<"Memory Failed!";
   return;
 } 
 head->data=1;       //Number from 1 
 head->next=NULL;    //At first, the whole linked list has only one Node. This Node has two fields, data and next
                     //data starts from 1 and next points to NULL. A total of N nodes are required. Now one is created and N-1 more nodes are required 
    p=head;             //The head cannot be changed before it can find the starting position of the linked list. At the beginning, p also points to the first node
                     //p will be used later. It is easy to create the remaining N-1 nodes 
       
 //To create a linked list by tail interpolation, there is already a node 1, and the remaining n-1 nodes need to be created 
 for(int i=2;i<=N;i++)
 {
  r=(Node*)malloc(sizeof(Node)); 
  r->data=i;
  r->next=NULL;
  //Insert Knot  
  p->next=r;
  p=r;
  
 }
 //Create circular linked list
 p->next=head;   //The next of the last node points to the head node
 p=head;         //For subsequent convenience, point p to the header node
 
 //Simulation of Joseph Ring
 while(p->next!= p)  //If p's next=p, there is only one element at present 
 {
  for(int i=1;i<M;i++)  //Out when the check-in number is M 
  {
     r=p;   //Keep the previous node out 
     p=p->next; //p refers to the node to be out, and the previous node needs to be retained
  }
  // output
  cout<<p->data<<" ";
  r->next=p->next;    //The purpose of deleting p. where does p point  
  p=p->next;  //Update p and report again 
 } 
 cout<<p->data; 
}
 
int main()
{
 ysflb(10,3);
 return 0;
} 

Of course, in addition to these two, there is another algorithm called recursion. The code of recursion algorithm is very short, but his idea is very rare. I'll give you a rough idea

int ysfh(int n,int m,int i)//There are n people who are out when they report to the number m. find the number of the i-th person who is out
{
  if(i==1)
     return(m-1+n)%n;
  return (ysfh(n-1,m,i-1)+m)%n;
}

This code is only the embodiment of the core idea. If you want to thoroughly understand it, you must understand the above two algorithms. Well, the above is what I introduced.