[classic algorithm problem] continued
Leetcode 0042 connected to rainwater
Title Description: Leetcode 0042 connected to rainwater
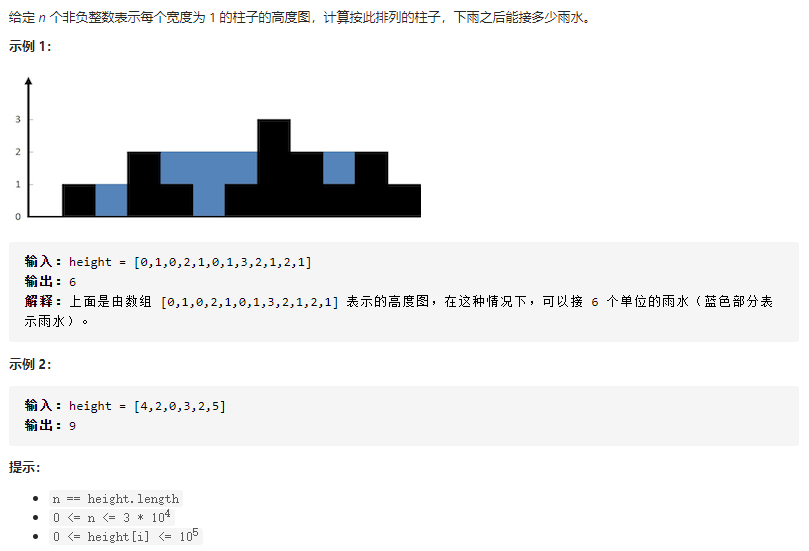
analysis
-
The test site of this question: array.
-
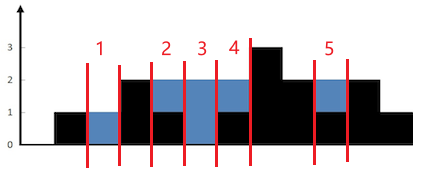
Core idea: we calculate the amount of water that can be stored at each location, and finally add it together to get the answer. As shown in the figure below, the amount of water in five places can be added together:
-
So how to solve the rainwater that can be stored at each location? We can preprocess two arrays left_max and right_max. left_max[i] represents the highest column in height[0]~height[i], right_max[i] represents the highest column in height[i]~height[n-1].
-
Then for position I, the rainwater that can be stored is: min(left_max[i], right_max[i]) - height[i].
-
This question is actually Leetcode 0407 connected to rainwater II A simple version. This problem is a two-dimensional version, Leetcode 0407 connected to rainwater II It's a 3D version.
code
- C++
class Solution {
public:
int trap(vector<int> &height) {
int n = height.size();
if (n == 0) return 0;
vector<int> left_max(n), right_max(n);
left_max[0] = height[0];
for (int i = 1; i < n; i++) left_max[i] = max(left_max[i - 1], height[i]);
right_max[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; i--) right_max[i] = max(right_max[i + 1], height[i]);
int res = 0;
for (int i = 0; i < n; i++) res += min(left_max[i], right_max[i]) - height[i];
return res;
}
};
- Java
class Solution {
public int trap(int[] height) {
int n = height.length;
if (n == 0) return 0;
int[] left_max = new int[n], right_max = new int[n];
left_max[0] = height[0];
for (int i = 1; i < n; i++) left_max[i] = Math.max(left_max[i - 1], height[i]);
right_max[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; i--) right_max[i] = Math.max(right_max[i + 1], height[i]);
int res = 0;
for (int i = 0; i < n; i++) res += Math.min(left_max[i], right_max[i]) - height[i];
return res;
}
}
- Python
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
if n == 0:
return 0
left_max = [0 for _ in range(n)]
right_max = [0 for _ in range(n)]
left_max[0] = height[0]
for i in range(1, n):
left_max[i] = max(left_max[i - 1], height[i])
right_max[n - 1] = height[n - 1]
for i in range(n - 2, -1, -1):
right_max[i] = max(right_max[i + 1], height[i])
res = 0
for i in range(n):
res += min(left_max[i], right_max[i]) - height[i]
return res
Spatiotemporal complexity analysis
-
Time complexity: O ( n ) O(n) O(n). N is the length of the array.
-
Space complexity: O ( n ) O(n) O(n). N is the length of the array.
Leetcode 0407 connected to rainwater II
Title Description: Leetcode 0407 connected to rainwater II

analysis
-
The test site of this question: dijkstra.
-
For the shortest path of the cell, please refer to website.
-
and Leetcode 0042 connected to rainwater The method is similar. We need to find the minimum value of the maximum value in all paths from the current position to the sea (there are multiple paths from this point to the sea, and each path has a maximum value. We need to find the minimum one among these maximum values). This minimum value is the height of the point after rain.
-
Similar to the shortest path problem, the shortest path problem is to solve the minimum value of the sum of paths; The problem here is to find the minimum value of the maximum value in all paths. This problem can be solved by the shortest path. The following uses the idea of dijkstea to solve this problem.
-
The starting point of this problem can be set as the sea, which is equivalent to a new virtual source point s. Each grid around from s is connected with an edge with an edge weight of 0. All points that cannot be reached from the starting point are marked as positive infinity, and then find the shortest path of a single source from s (the edge weight from a to b is defined as the height of b).
-
When implementing the code, you do not need to really establish s, but directly add all the points reached by s to the priority queue.
-
set up d i s t [ i ] [ j ] dist[i][j] dist[i][j] indicates from s to ( i , j ) (i, j) (i,j) the minimum value of the maximum edge weight in all paths, if from ( i , j ) (i, j) (i,j) reachable ( x , y ) (x, y) (x,y), then there must be: d i s t [ x ] [ y ] ≤ m a x ( d i s t [ i ] [ j ] , h [ x ] [ y ] ) dist[x][y] \le max(dist[i][j], h[x][y]) dist[x][y]≤max(dist[i][j],h[x][y]). The explanation is as follows:

-
Another problem is to prove that dijkstea algorithm can be used to solve this problem. This question can prove the elements of joining the team (assuming ( x , y ) (x, y) (x,y)) is the minimum value and cannot be updated by other points.
-
First of all, it is legal for the surrounding elements to join the team, because it is the minimum value of the maximum value of all paths from the current point to the sea. Because each path contains this point, the minimum value is greater than or equal to this point, and because there is a path to get this point, the surrounding values are the corresponding weights.
-
When point b in the graph is extended for the first time, it is assumed that it is extended from the adjacent point a to the other three points around b, either in the queue or not in the queue, so the final dist value corresponding to point b is larger. Here, we want to explain that the dist value of the extended point is increasing.
code
- C++
class Solution {
public:
static const int N = 210;
bool st[N][N]; // The judgment array is true, which means that the answer has been found at this point
struct Node {
int x, y, d; // d: The minimum value of the maximum edge weight in all paths reaching (x, y), dist in the above analysis
bool operator<(const Node &t) const {
return d > t.d; // The default is large top heap, and small top heap is required
}
};
int trapRainWater(vector<vector<int>> &h) {
int n = h.size(), m = h[0].size();
int res = 0;
priority_queue<Node> heap;
// Add the surrounding points to the priority queue
for (int i = 0; i < n; i++) {
heap.push({i, 0, h[i][0]});
heap.push({i, m - 1, h[i][m - 1]});
st[i][0] = st[i][m - 1] = true;
}
for (int i = 1; i < m - 1; i++) {
heap.push({0, i, h[0][i]});
heap.push({n - 1, i, h[n - 1][i]});
st[0][i] = st[n - 1][i] = true;
}
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
while (heap.size()) {
Node t = heap.top();
heap.pop();
for (int i = 0; i < 4; i++) {
int x = t.x + dx[i], y = t.y + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && !st[x][y]) {
st[x][y] = true;
if (h[x][y] < t.d) res += t.d - h[x][y];
heap.push({x, y, max(t.d, h[x][y])});
}
}
}
return res;
}
};
- Java
class Solution {
static final int N = 210; // However, there is a (200200) matrix at the time of submission
boolean[][] st = new boolean[N][N]; // The judgment array is true, which means that the answer has been found at this point
static class Node implements Comparable<Node> {
int x, y, d; // d: The minimum value of the maximum edge weight in all paths to (x, y)
public Node(int x, int y, int d) {
this.x = x;
this.y = y;
this.d = d;
}
@Override
public int compareTo(Node o) {
return d - o.d; // The default is small top heap, which needs to be used
}
}
public int trapRainWater(int[][] h) {
int n = h.length, m = h[0].length;
int res = 0;
PriorityQueue<Node> heap = new PriorityQueue<>();
// Add the surrounding points to the priority queue
for (int i = 0; i < n; i++) {
heap.add(new Node(i, 0, h[i][0]));
heap.add(new Node(i, m - 1, h[i][m - 1]));
st[i][0] = st[i][m - 1] = true;
}
for (int i = 1; i < m - 1; i++) {
heap.add(new Node(0, i, h[0][i]));
heap.add(new Node(n - 1, i, h[n - 1][i]));
st[0][i] = st[n - 1][i] = true;
}
int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};
while (!heap.isEmpty()) {
Node t = heap.remove();
for (int i = 0; i < 4; i++) {
int x = t.x + dx[i], y = t.y + dy[i];
if (x < 0 || x >= n || y < 0 || y >= m || st[x][y]) continue;
st[x][y] = true;
if (h[x][y] < t.d) res += t.d - h[x][y];
heap.add(new Node(x, y, Math.max(h[x][y], t.d)));
}
}
return res;
}
}
Spatiotemporal complexity analysis
-
Time complexity: O ( n × l o g ( n ) ) O(n \times log(n)) O(n × log(n)). N is the side length of the array. Let n be the larger of the two sides.
-
Space complexity: O ( n 2 ) O(n^2) O(n2). N is the length of the array.