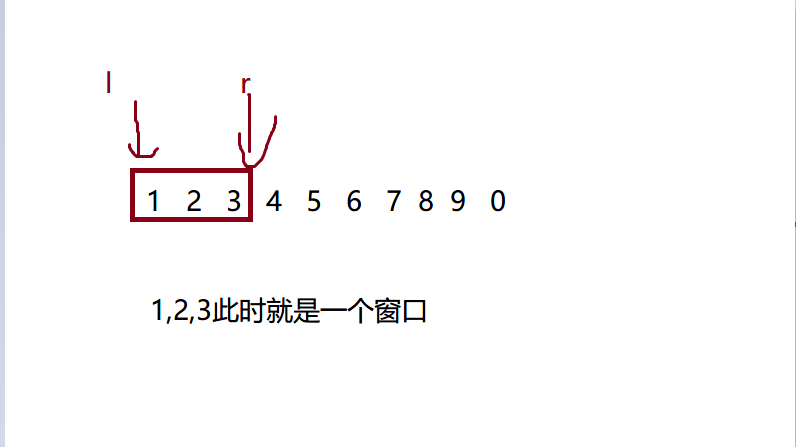
Simple concept of sliding window
Sliding window is a hypothetical data structure. The window we implement in this article can quickly find the maximum and minimum value of the interval
The operation efficiency is also excellent in some problems that do not go back in the interval
Set the left boundary of the window as l and the right boundary as r, (it is specified that l < = r is constant)
We can enter the number from the right side of the window by sliding the right boundary
You can also slide the left border to show the number from the left side of the window
Sliding window for interval maximum (leetcode239)
Title Description:
Give you an integer array nums, with a sliding window of size k moving from the leftmost side of the array to the rightmost side of the array. You can only see k numbers in the sliding window. The sliding window moves only one bit to the right at a time.
Returns the maximum value in the sliding window.
Thinking solution
We can realize the structure of our maximum window through the double ended queue, which stores the subscripts in the array
The order of the number corresponding to the subscript must always be maintained in the double ended queue
Keep moving the window. If the number of entries will break the balance from large to small (that is, the new number is greater than the end of the queue), the number will continue to appear at the end of the queue until the requirements of the double ended queue are met, and then insert the current number
Dynamic diagram demonstration:
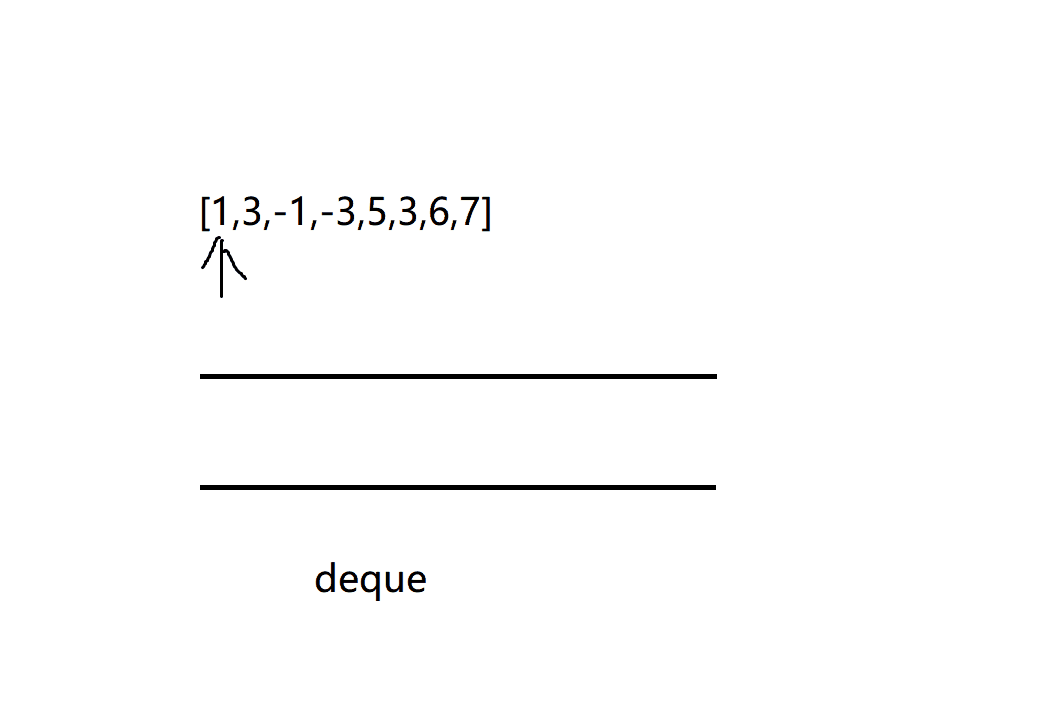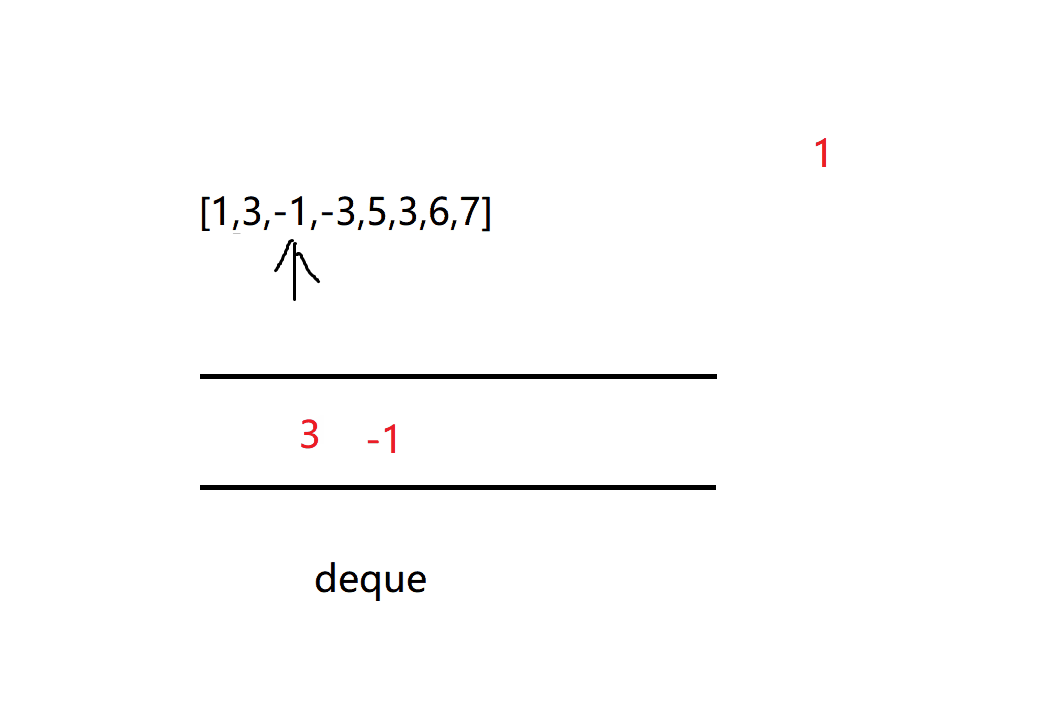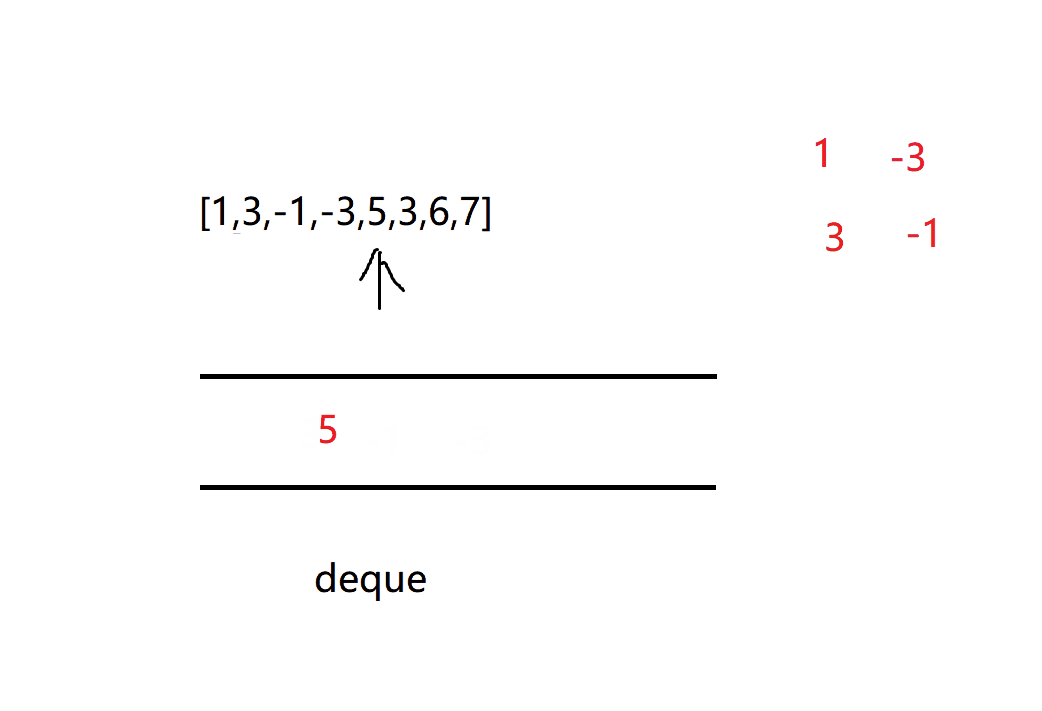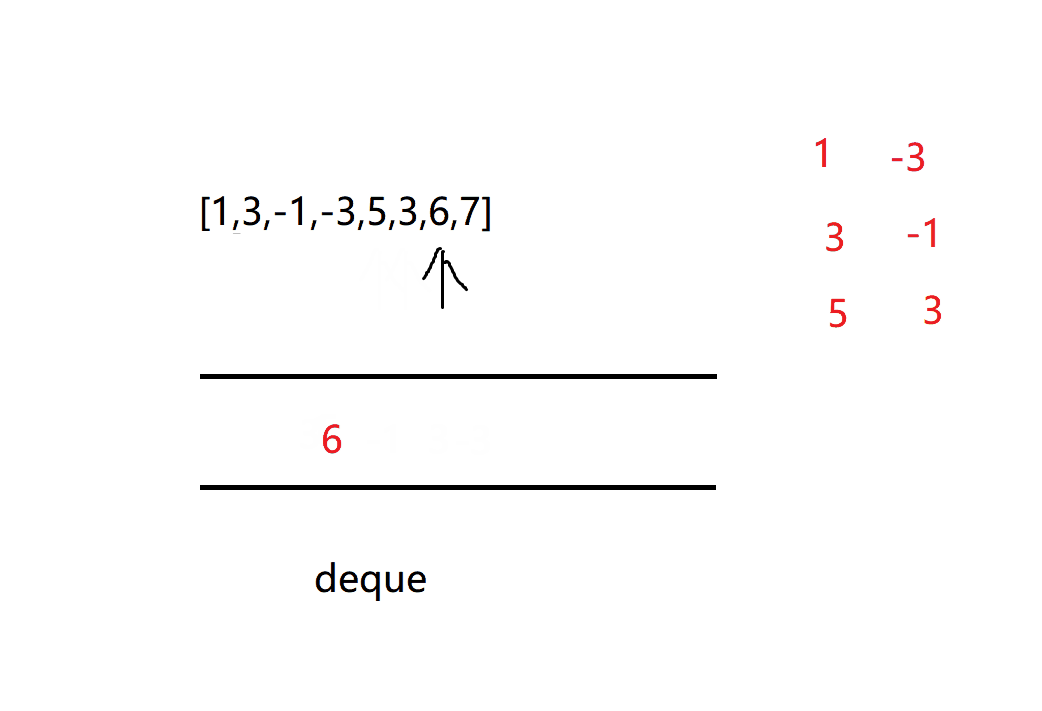
It can be expressed in a fixed size window. As long as the window contains this number, the maximum value of this window will always be the top of the queue
Until there is no maximum value in the window, pop it up from the left
Code implementation and comments:
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n=nums.size();
vector<int>ans;
deque<int>qmax;//Maintain maximum queue
for(int r=0;r<n;r++)
{
while(!qmax.empty()&&nums[qmax.back()]<=nums[r])
{
qmax.pop_back();//This is the structure of maintaining the queue from large to small
//Pop up all numbers smaller than the new number at the end of the team
}
qmax.push_back(r);
if(qmax.front()==r-k)
{
qmax.pop_front();//This is the case where the subscript corresponding to the maximum value is no longer in the window
//Because r-l=k
}
if(r>=k-1)
{
ans.push_back(nums[qmax.front()]);
//When the window is formed, add the number directly
}
}
return ans;
}
};
Find the number of subarrays that meet the requirements
Title Description:
Given an array arr and an integer sum
If a subarray (which must be connected) meets the maximum minimum value < = sum of the subsequence, it is said that the subarray meets the requirements
Returns the number of subsequences that meet the requirements
Solution ideas:
We can draw two conclusions first:
- If a subarray meets the requirements, all subarrays of this subarray meet the requirements
- If a subarray does not meet the requirements, the arrays with it as a subarray do not meet the requirements
Why?
We know that our final requirement is Max min
If the requirements are met, then max min < sum should be established
Obviously, it is easy to see that the maximum value of its sub array will only be smaller than the maximum value of this array, and the minimum value will only be larger than the minimum value of this array,
So in this case, max min will only decrease
The same can be proved if the requirements are not met
So we can:
Initially, put the window to the left, maintain the maximum and minimum values of the window, and constantly update the right boundary of the window until it does not meet the requirements
According to conclusion 1, all subarrays starting from L meet the requirements * * (subarrays from L to l+1;l to l+2;l to l+3...)**
According to conclusion 1, we can update l without updating r
Codes and comments:
int AllLessNumSubArray(vector<int>& nums, int sum)
{
int n = nums.size();
deque<int>qmax;
deque<int>qmin;
int ans = 0;
int r = 0;
for (int l = 0; l < n; l++)
{
while (r < n)
{
while (!qmax.empty() && nums[qmax.back()] <= nums[r])
{
qmax.pop_back();
}
qmax.push_back(r);
while (!qmin.empty() && nums[qmin.back()] >= nums[r])
{
qmin.pop_back();
}
qmin.push_back(r);
//The above is to maintain the maximum and minimum queue
//The following is the sliding window
if (nums[qmax.front()] - nums[qmin.front()] <= sum)
{
r++;
}
else
{
break;
}
}
ans += r - l;
//Update expired elements
if (qmax.front() == l)
{
qmax.pop_front();
}
if (qmin.front() == l)
{
qmin.pop_front();
}
}
return ans;
}
The above questions clearly require the maximum and minimum value of the window. The following question is not obvious
The best starting point of gas station
Title Description
Here are two arrays, gas and cost
In fact, gas[i] refers to the fuel consumption of No. I gas station, and cost[i] refers to the fuel consumption from No. I to i+1 gas station
The initial fuel volume of the vehicle is 0
Returns a bool type, which indicates whether the car can complete a circle when starting from No. i gas station, and can only make a circle counterclockwise
For example:
gas=[1,1,3,1]
cost=[2,2,1,1]
The figure is as follows:
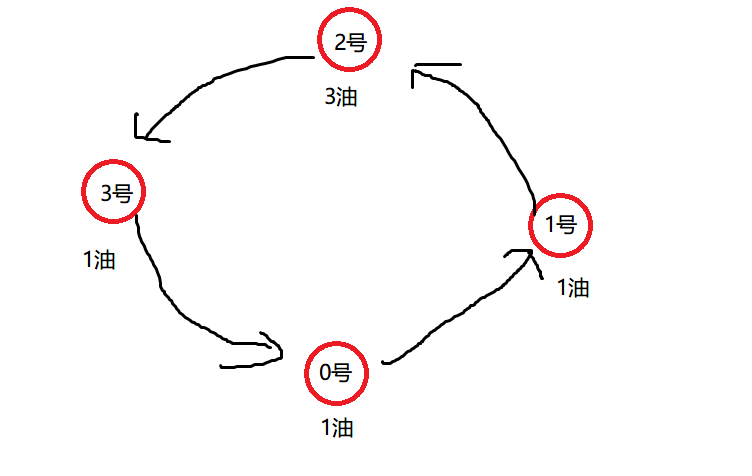
If you start from gas station 0, cost[0] is 2, but gas[0]=1, the car can't get to gas station 1, so ans[0] returns false
Overall return: [0,0,1,0]
Solution ideas:
We can do a processing before solving the problem
First, subtract the number corresponding to each position of gas and cost to obtain the processed array nums
for (int i = 0; i < n; i++)
{
nums[i] = gas[i] - cost[i];
}
In this way, we can show whether we can get to the next station from a certain station. If the result is negative, we can't get there
We can find the prefix sum. If there is a negative number halfway, it means that this circle cannot be completed
For example, the prefix and starting from 0 indicate the amount of remaining fuel passing through each gas station halfway from 0
The prefix and starting from 1 indicate starting from 1, and so on
Because we have to go around, we should deal with twice the size of the original array (don't start from 0?)
int m=n<<1;
for (int i = 0; i < n; i++)
{
nums[i] = gas[i] - cost[i];
nums[i + n] = gas[i] - cost[i];
}
for (int i = 1; i < m; i++)
{
nums[i] += nums[i - 1];
}
The size of the window in this question is required to be the same as that of the original array. We can deal with our array as follows:
Maintain minimum window
Obviously, if the minimum value is not negative, there is no negative number in the window
When updating the array window, we remember to subtract the value in the window from the value in front of the left boundary of the window, so as to be the correct prefix and prefix starting from l
Directly judge whether the current minimum value is less than 0
Code is comment:
vector<bool> GasStation(vector<int>& gas, vector<int>& cost)
{
int n = gas.size();
int m = n << 1;
vector<bool>ans(n, false);
int* nums = new int[m];
for (int i = 0; i < n; i++)
{
nums[i] = gas[i] - cost[i];
nums[i + n] = gas[i] - cost[i];
}
for (int i = 1; i < m; i++)
{
nums[i] += nums[i - 1];
}
deque<int>w;
//Initialization window
for (int i = 0; i < n; i++)
{
while (!w.empty() && nums[w.back()] >= nums[i])
{
w.pop_back();
}
w.push_back(i);
}
for (int offset = 0, i = 0, j = n; j < m; offset = nums[i++], j++)
{
//offset represents the number in front of the window and w always maintains the minimum value of the window
//i left boundary, j right boundary
if (nums[w.front()] - offset >= 0)
{
ans[i] = true;
}
if (w.front() == i)
{
w.pop_front();
}
while (!w.empty() && nums[w.back()] >= nums[j])
{
w.pop_back();
}
w.push_back(j);
}
delete[]nums;
return ans;
}