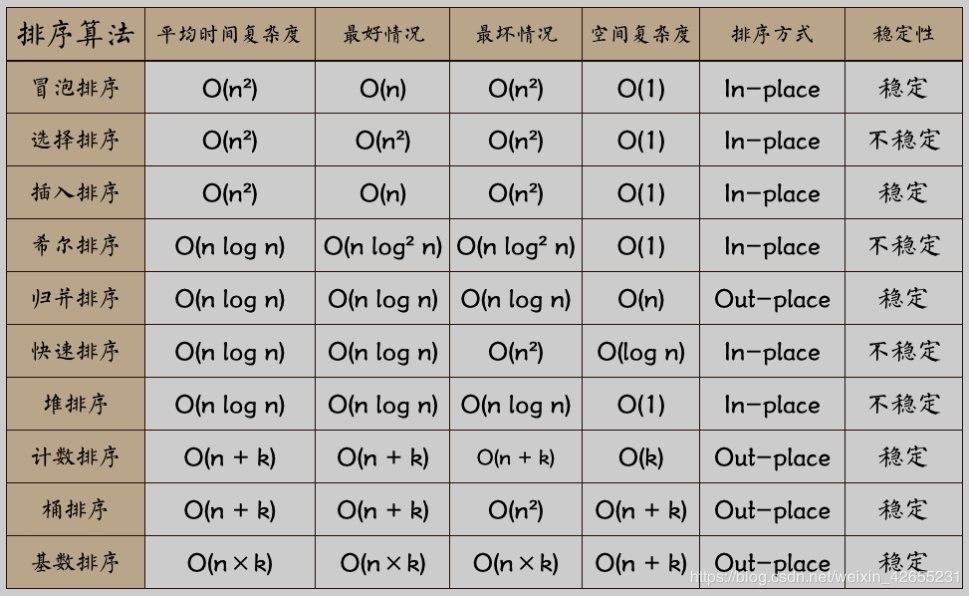
Sorting algorithm directory

1. Direct insert sort
2. Binary Insertion Sort
3. Shell Sort
4. Bubble sorting
5. Quick sort
6. Select sort
7. Merge sort
8. Heap sort

1. Insert sorting directly

Direct insert sort

Algorithmic thought

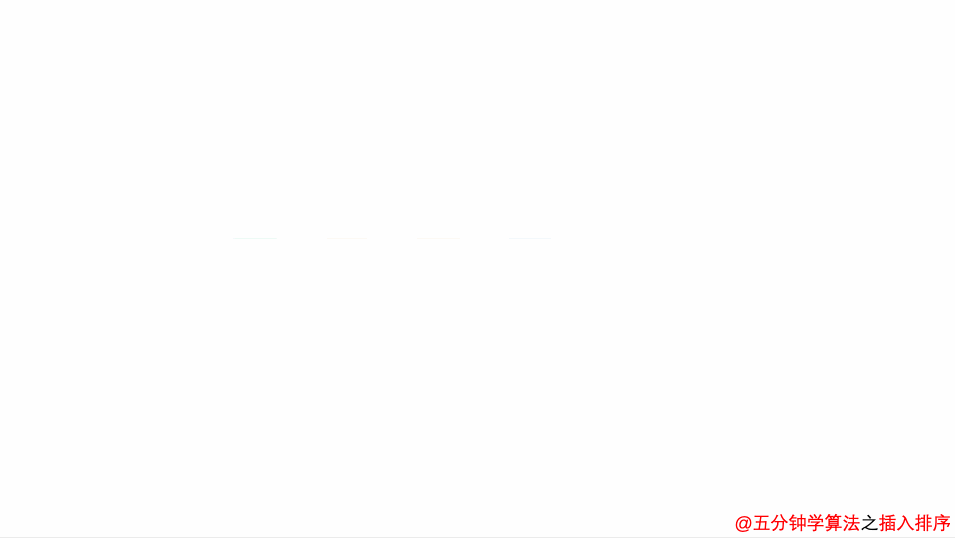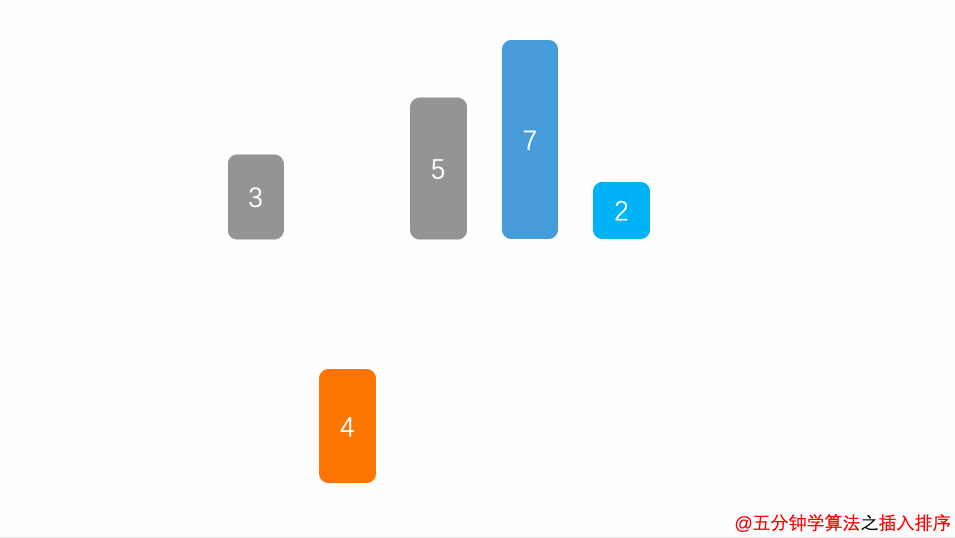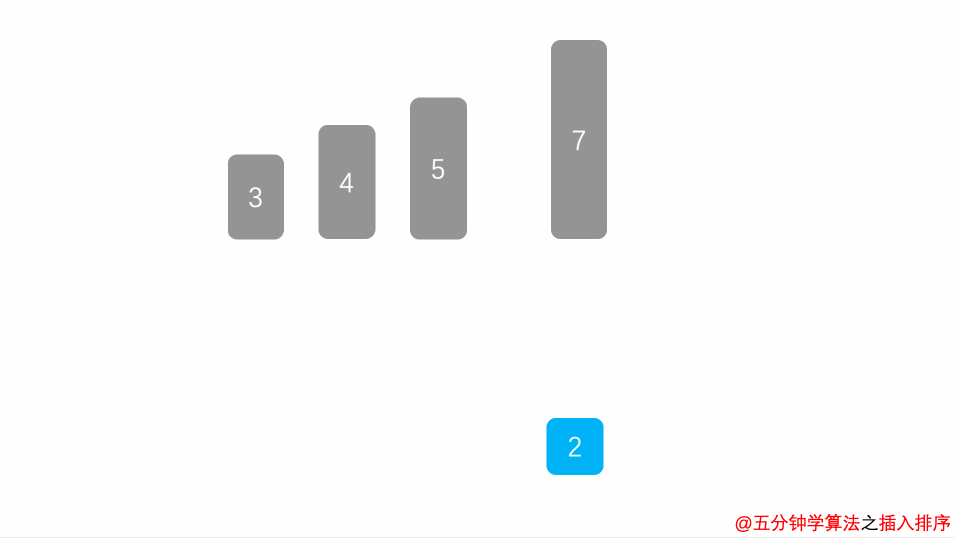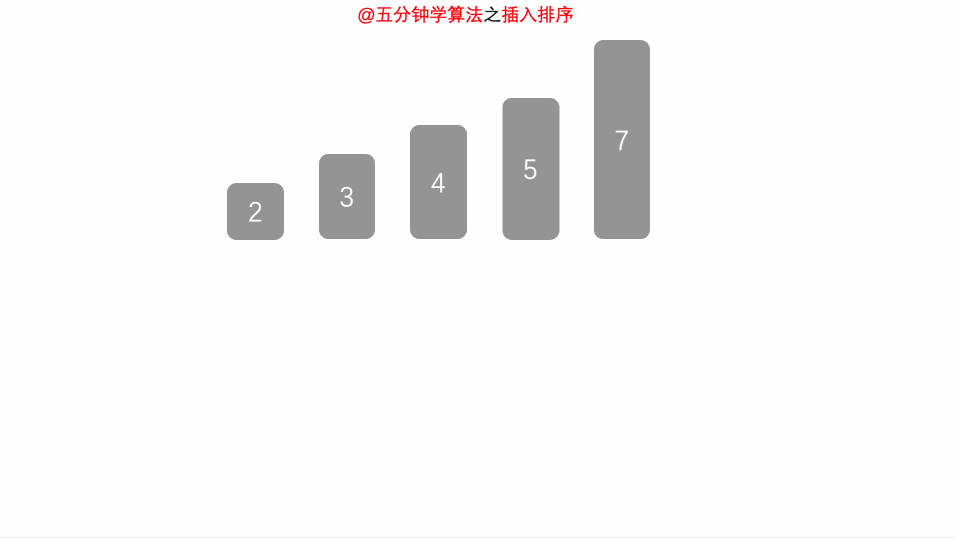
Divide the sequence into ordered part and unordered part, select the elements from the unordered part, compare with the ordered part, find the appropriate position, move the original element back, and insert the element into the corresponding position until all records are inserted.

Animation demonstration

Time complexity

1. Preferably - O ( n ) O(n) O(n) sequence ordering
2. Worst case - O ( n 2 ) O(n^2) O(n2) sequence reverse order
3. Average - O ( n 2 ) O(n^2) O(n2)

Space complexity O (1)

1. Temporary variable temp without sentry
2. With sentry a[0]

stability

stable

Applicability

1. Sequence table
2. Linked list

Algorithm characteristics

1. Stable sorting
2. The algorithm is simple and easy to implement
3. Sequential list and linked list can be realized
4. It is more suitable for the situation that the initial records are basically orderly. When n is large, the time complexity is high and should not be used.

Core code

//Direct insertion sort (no sentry) 
void InsertSort(int a[], int n){
	int i, j , temp;
	for(i = 1; i < n; i ++){
		if(a[i] < a[i - 1]){
			temp = a[i];
			for(j = i - 1; j >= 0 && temp < a[j]; j --){
				a[j + 1] = a[j];
			}
			a[j + 1] = temp;
		}
	}
}

//Direct insertion sort (with sentinel) 
void InsertSort2(int a[], int n){
	int i , j;
	for(i = 2; i <= n; i ++){
		if(a[i] < a[i - 1]){
			a[0] = a[i];
			for(j = i - 1; a[0] < a[j]; j --){
				a[j + 1] = a[j];
			}
			a[j + 1] = a[0];
		}
	}
} 

Full code (no sentry)

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <fstream>

using namespace std;
const int N = 10;
int data[N], idex;

//Direct insertion sort (no sentry) 
void InsertSort(int a[], int n){
	int i, j , temp;
	for(i = 1; i < n; i ++){
		if(a[i] < a[i - 1]){
			temp = a[i];
			for(j = i - 1; j >= 0 && temp < a[j]; j --){
				a[j + 1] = a[j];
			}
			a[j + 1] = temp;
		}
	}
}

int main(){
	ifstream infile;
	infile.open("D:\\study\\data structure\\Chapter 8 sorting\\in.txt",ios::in);
	ofstream outfile;
	outfile.open("D:\\study\\data structure\\Chapter 8 sorting\\out.txt",ios::out);
	if (!infile.is_open()) { 
        cout << "Open file failure" << endl; 
    }
    while(!infile.eof()){
    	infile >> data[idex ++];
	}
	
	//Original array element 
	for(int i = 0; i < N; i ++) cout << data[i] << ' '; cout << endl;
	
	//After insertion sorting without sentry 
	InsertSort(data,idex);
	for(int i = 0; i < N; i ++) cout << data[i] << ' '; cout << endl;
	
	for(int i = 0; i < N; i ++)	outfile << data[i] << ' '; outfile << endl;
	
	infile.close();
	outfile.close();
	return 0;
} 

Input case (in.txt)

13 69 86 99 59 23 64 32 86 72

Output result (out.txt)

13 23 32 59 64 69 72 86 86 99

Full code (with sentry)

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <fstream>

using namespace std;
const int N = 20;
int data[N], idex,num = 10;

//Direct insertion sort (with sentinel) 
void InsertSort2(int a[], int n){
	int i , j;
	for(i = 2; i <= n; i ++){
		if(a[i] < a[i - 1]){
			a[0] = a[i];
			for(j = i - 1; a[0] < a[j]; j --){
				a[j + 1] = a[j];
			}
			a[j + 1] = a[0];
		}
	}
} 

int main(){
	ifstream infile;
	infile.open("D:\\study\\data structure\\Chapter 8 sorting\\in.txt",ios::in);
	ofstream outfile;
	outfile.open("D:\\study\\data structure\\Chapter 8 sorting\\out.txt",ios::out);
	if (!infile.is_open()) { 
        cout << "Open file failure" << endl; 
    }
	
	idex = 1;
    while(!infile.eof()){
    	infile >> data[idex ++];
	}
	
	//Original array element 
	for(int i = 1; i <= num; i ++) cout << data[i] << ' '; cout << endl;
	
	//After insertion sorting without sentry 
	InsertSort2(data,num);
	//sort(data + 1 ,data + num + 1);
	for(int i = 1; i <= num; i ++) cout << data[i] << ' '; cout << endl;
	
	//Output sorted file data 
	for(int i = 1; i <= num; i ++)	outfile << data[i] << ' '; outfile << endl;
	
	infile.close();
	outfile.close();
	return 0;
} //Direct insertion sort (with sentinel)

Input case (in.txt)

13 69 86 99 59 23 64 32 86 72

Output result (out.txt)

13 23 32 59 64 69 72 86 86 99

Return sorting algorithm directory

2. Sort by half insertion

Binary Insertion Sort

Algorithmic thought

Set three variables l o w , h i g h , m i d ， low,high,mid， low,high,mid m i d = ( l o w + h i g h ) / 2 mid = (low + high) / 2 mid=(low+high)/2, if a [ m i d ] > k e y a[mid] > key A [mid] > key, the h i g h = m i d − 1 high = mid - 1 high=mid − 1, otherwise l o w = m i d + 1 low = mid + 1 low=mid+1 until l o w > h i g low > hig Stop the cycle when low > hig. Do the above processing for each element in the sequence, find the appropriate position, move other elements back and insert them.

Time complexity

1. Preferably - O ( n l o g n ) O(nlogn) O(nlogn)
2. Worst case - O ( n 2 ) O(n^2) O(n2)
3. Average - O ( n 2 ) O(n^2) O(n2)

Note: the number of comparisons has nothing to do with the initial state of the sequence to be arranged, but only depends on the number of elements in the table

Space complexity O (1)

1. Temporary variable temp without sentry
2. With sentry a[0]

stability

stable

Applicability

Applies only to sequence tables

Algorithm characteristics

1. Stable sorting
2. Because half search is required, it can only be used for sequential tables, not linked lists
3. It is suitable for the case where the initial record is out of order and n is large.
4. Compared with direct insertion sorting, the number of comparisons is greatly reduced.

code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;
int num, idx;//num number of stored elements 

int data[N]; 

//Split insertion sort (with sentry) 
void BinaryInsertSort(int a[], int n){
	int i, j, low, high, mid;
	for(i = 2; i <= n; i ++){
		a[0] = a[i];//Assign the band insertion element to the sentinel
		low = 1, high = i - 1;//Binary search between 1~i-1 
		while(low <= high){//High > low loop end
		 mid = low + high >> 1;
		 if(a[0] < a[mid]) high = mid - 1;
		 else low = mid + 1;//Even if the elements are equal, they are inserted after them to maintain sorting stability
		}
		for(j = i - 1; j >= high + 1; j --){// The element to be inserted shall be located at high+1
		 a[j + 1] = a[j];//Move ordered elements back 
		}
		a[high + 1] = a[0];//Insert the element to be inserted into the correct position
	}
}

int main(){
	//read file 
	ifstream infile;
	infile.open("D:\\study\\data structure\\Chapter 8 sorting\\in.txt",ios::in);
	
	//Write file
	ofstream outfile; 
	outfile.open("D:\\study\\data structure\\Chapter 8 sorting\\out.txt",ios::out);
	
	if(!infile.is_open()){//Judge whether the file is opened successfully 
		cout << "file open failure !" << endl;
	}
	
	infile >> num;
	while(num != 0){
		infile >> data[++ idx];
		num --;
	}
	
	num = idx;
	for(int i = 1; i <= num; i ++) cout << data[i] << ' '; cout << endl;
	
	BinaryInsertSort(data, idx);
	//sort(data,data + num);
	for(int i = 1; i <= num; i ++) cout << data[i] << ' '; cout << endl; 
	
	idx = 1;
	outfile << num; outfile << endl;
	while(num != 0){
		outfile << data[idx ++] << ' ';
		num --;
	}
	outfile << endl;
	
	//Close file 
	infile.close();
	outfile.close();
	return 0;
} 

Input data (in.txt)

10
13 69 86 99 59 23 64 32 86 72

Output data (out.txt)

10
13 23 32 59 64 69 72 86 86 99 

Return sorting algorithm directory

3. Hill sort

Shell Sort

Algorithmic thought

Firstly, the sequence is divided into several subsequences, and then each subsequence is directly inserted and sorted. When the sequence is basically ordered, the whole sequence is directly inserted and sorted once. That is, first pursue the partial order of the elements in the table, and then gradually approach the global order.

advantage:

Elements with small keyword values can be moved to the front quickly, and when the sequence is basically in order, the direct insertion sorting time efficiency will be greatly improved.

Time complexity

1. Preferably - nothing nothing nothing
2. Worst case - O ( n 2 ) O(n^2) O(n2)
3. Average - O ( n 1.3 ) O(n^{1.3}) O(n1.3)

Demo animation

Space complexity O (1)

Use array number one element a[0]

stability

instable

Applicability

Applies only to sequence tables

Algorithm characteristics

1. The jumping movement of records causes the sorting method to be unstable
2. It can only be used for sequential structure, not chain structure
3. The incremental sequence can have various methods, but the value in the incremental sequence should have no common factor other than division, and the last incremental value must be 1
4. The total comparison times and movement times of records are less than those of direct insertion sorting. When n months are old, the effect is more obvious. It is suitable for the case when the initial record is out of order and N is large.

Core code

//Shell Sort  
void ShellSort(int a[], int n){
	int d, i, j;
	for(d = n / 2; d >= 1; d /= 2){//d is increment, and the increment sequence is halved in turn (recommended by the original author of the algorithm) 
		for(i = d + 1; i <= n; i ++){//Processing local sequences 
			if(a[i] < a[i - d]){
				a[0] = a[i];//Staging current pending elements 
				for(j = i - d; j > 0 && a[0] < a[j]; j -= d){
					a[j + d] = a[j];//Local element backward 
				}
				a[j + d] = a[0];//Insert the current element at the appropriate location 
			}
		}
	}
}

Complete code

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx;

//Shell Sort  
void ShellSort(int a[], int n){
	int d, i, j;
	for(d = n / 2; d >= 1; d /= 2){//d is increment, and the increment sequence is halved in turn (recommended by the original author of the algorithm) 
		for(i = d + 1; i <= n; i ++){//Processing local sequences 
			if(a[i] < a[i - d]){
				a[0] = a[i];//Staging current pending elements 
				for(j = i - d; j > 0 && a[0] < a[j]; j -= d){
					a[j + d] = a[j];//Local element backward 
				}
				a[j + d] = a[0];//Insert the current element at the appropriate location 
			}
		}
	}
}

int main(){
	//Open file 
	ifstream infile;
	infile.open("D:\\study\\data structure\\Chapter 8 sorting\\in.txt", ios::in);
	
	//Write file 
	ofstream outfile;
	outfile.open("D:\\study\\data structure\\Chapter 8 sorting\\out.txt", ios::out);
	
	if(!infile.is_open()){//Judge whether the file is opened successfully 
		cout << "file open failure!" << endl;
	}
	
	infile >> num;//Number of read elements 
	while(num --){//Copy the elements in the file to the data[1...n] array
		infile >> data[++ idx];
	}
	
	cout << "Element sequence before sorting:" << endl;
	for(int i = 1; i <= idx; i ++) cout << data[i] << ' '; cout << endl;
	
	cout << "use sort Function sorted sequence: " << endl;
	sort(data + 1, data + 1 + idx); 
	for(int i = 1; i <= idx;  i++) cout << data[i] << ' '; cout << endl;
	
	ShellSort(data, idx);
	cout << "After using Hill sorting, the sequence is:" << endl;
	for(int i = 1; i <= idx;  i++) cout << data[i] << ' '; cout << endl;
	
	num = idx, idx = 0, outfile << num << endl;//Write data num and write at end of line \ n 
	while(num --){
		outfile << data[++ idx] << ' ';//Write the sorted data to the file 
	}
	outfile << endl;//Write terminator to end of file \ n 
	
	
	//Close file 
	infile.close();
	outfile.close();
	return 0;
}

Input data (in.txt)

10
13 69 86 99 59 23 64 32 86 72

Output data (out.txt)

10
13 23 32 59 64 69 72 86 86 99 

Return sorting algorithm directory

4. Bubble sorting

Bubble sorting

Algorithmic thought

Compare the values of adjacent elements from front to back (or from back to front). If it is in reverse order, exchange them until the sequence comparison is completed. This process is called one bubble sorting. Sorting can be completed by n-1 bubble sorting.

Note:

1. Each sorting can move an element to the final position, and the elements whose final position has been determined do not need to be compared in subsequent processing
2. If there is no exchange in a sorting process, the algorithm can end in advance

Time complexity

1. Preferably - O ( n ) O(n) O(n) ordered sequence
2. Worst case - O ( n 2 ) O(n^2) O(n2) reverse sequence
3. Average - O ( n 1.3 ) O(n^ {1.3}) O(n1.3)

Demo animation

Spatial complexity

Use temporary variables---- O ( 1 ) O(1) O(1)

stability

stable

Applicability

1. Sequence table
2. Linked list

Algorithm characteristics

1. Stable sorting
2. It can be used for chain storage and sequential storage
3. The average time performance of the algorithm is worse than that of direct insertion sorting. When the initial sequence is out of order and n is large, this algorithm is not suitable

Core code

//Bubble sorting 
void BubbleSort(int a[], int n){
	for(int i = 0; i < n - 1; i ++){// Control times, n-1 times 
		bool flag = false;//Mark whether there are elements exchanged in each trip 
		for(int j = n - 1; j > i; j --){//Enumerate from back to front 
			if(a[j] < a[j - 1]){
			swap(a[j], a[j - 1]);
			flag = true;//Exchange occurs 
			} 
		}
		if(flag == false) return;//There is no exchange in this trip, that is, all elements are in order 
	}
}

Optimization process

1. Simple writing

//Ascending sort
void bubble_sort(int a[], int len){//Enumeration. len is the length of the array
    for(int i = 0; i < len; i ++){//Enumerating comparison elements
        for(int j = 0; j < len - i - 1; j ++){
            if(a[j] > a[j + 1]){//Reverse order, exchange
                int t = a[j];
                a[j] = a[j + 1];
                a[j + 1] = t;
            }
        }
    }
}

2. Primary optimization

Set a flag bit to indicate whether there is exchange in the current i-th pass. If yes, i+1 pass is required. If not, it indicates the current array
Sorting has been completed. Once it is found that the order has been arranged, it will immediately jump out of the loop to reduce the number of unnecessary comparisons

//Ascending sort
void bubble_sort(int a[], int len){
    for(int i = 0; i < len; i ++){
        bool flag = true;//Whether records are exchanged
        for(int j = 0; j < len - i - 1; j ++){
            if(a[j] > a[j + 1]){
                cnt ++;
                int t = a[j];
                a[j] = a[j + 1];
                a[j + 1] = t;
                flag = false;//Exchange occurs
            }
        }
        if(flag) break;//A certain trip has been completely arranged and you can exit directly
    }
}

3. Secondary optimization

Use a flag bit to record the subscript of the last position exchanged in the current i-th trip. When i+1 trip is carried out, only internal circulation is required
It's OK to ring to the marked position, because the elements in the later position are not transposed in the last trip, and it's impossible to change the position this time

//Ascending sort
void bubble_sort(int a[], int len){
    int pos;
    for(int i = 0; i < len; i ++){
        bool flag = true;
        for(int j = 0; j < len - i - 1; j ++){
            if(a[j] > a[j + 1]){
                cnt ++;
                int t = a[j];
                a[j] = a[j + 1];
                a[j + 1] = t;
                pos = j;//Record the location of the exchange
                flag = false;//Exchange occurs
            }
        }
        len = pos;//Record the last good location to update len
        if(flag) break;
    }
}

Summary:

The primary optimization is mainly to add a mark for the case that the order has been completely arranged in the middle and there is no need for subsequent comparison. It is judged according to the mark
Whether the previous array has been completely ordered. Once ordered, the loop exits immediately, reducing subsequent unnecessary comparisons

The secondary optimization code is mainly to add a pos variable on the basis of the previous one to record the last position of the exchange element in the last trip. The purpose is to skip it
The elements that have been ordered before are enumerated until the elements that have not been ordered

Complete code

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx;

//Bubble sorting 
void BubbleSort(int a[], int n){
	for(int i = 0; i < n - 1; i ++){// Control times, n-1 times 
		bool flag = false;//Mark whether there are elements exchanged in each trip 
		for(int j = n - 1; j > i; j --){//Enumerate from back to front 
			if(a[j] < a[j - 1]){
			swap(a[j], a[j - 1]);
			flag = true;//Exchange occurs 
			} 
		}
		if(flag == false) return;//There is no exchange in this trip, that is, all elements are in order 
	}
}

int main(){
	//Open file 
	ifstream infile;
	infile.open("D:\\study\\data structure\\Chapter 8 sorting\\in.txt", ios::in);
	
	//Write file 
	ofstream outfile;
	outfile.open("D:\\study\\data structure\\Chapter 8 sorting\\out.txt", ios::out);
	
	if(!infile.is_open()){//Judge whether the file is opened successfully 
		cout << "file open failure!" << endl;
	}
	
	infile >> num;//Number of read elements 
	while(num --){//Copy the elements in the file to the data[1...n] array
		infile >> data[idx ++];
	}
	
	cout << "Element sequence before sorting:" << endl;
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	cout << "use sort Function sorted sequence: " << endl;
	sort(data, data + idx); 
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	BubbleSort(data, idx);
	cout << "After bubble sorting, the sequence is:" << endl;
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	num = idx, idx = 0, outfile << num << endl;//Write data num and write at end of line \ n 
	while(num --){
		outfile << data[++ idx] << ' ';//Write the sorted data to the file 
	}
	outfile << endl;//Write terminator to end of file \ n 
	
	//Close file 
	infile.close();
	outfile.close();
	return 0;
}

Input data (in.txt)

10
13 69 86 99 59 23 64 32 86 72

Output data (out.txt)

10
13 23 32 59 64 69 72 86 86 99 

Return sorting algorithm directory

5. Quick sort

Quick sort

Algorithmic thought

In the to be sorted table a[0...n-1], take any element pivot as the pivot (or benchmark, usually the first element), and divide the to be sorted table into two independent parts a[0...k-1] and a[k + 1... N-1] through one sorting, so that all elements in a[0...k-1] are less than pivot, and all elements in a[k + 1... N - 1] are greater than or equal to pivot, then the pivot is placed in its final position a[k] This process becomes a "partition", and then recursively repeat the above process for the two sub tables respectively until there is only one element or empty in each part, that is, all elements are placed in their final position.

Time complexity

1. Preferably - O ( n l o g n ) O(nlogn) Uniform segmentation of O(nlogn) sequences
2. Worst case - O ( n 2 ) O(n^2) O(n2) sequence ordering
3. Average - O ( n l o g n ) O(nlogn) O(nlogn)

Demo animation

Spatial complexity

1. Preferably - O ( n l o g n ) O(nlogn) Uniform segmentation of O(nlogn) sequences
2. Worst case - O ( n ) O(n) O(n) sequence ordering

stability

instable

Applicability

Applies only to sequence tables

Algorithm characteristics

1. When n is large, on average, quick sort is the fastest of all internal sorting methods, so it is suitable for the case of disordered initial records and large n
2. The non sequential movement of records leads to the instability of the sorting method
3. It is necessary to locate the upper and lower bounds of the table in the sorting process, so it is only suitable for the sequential structure, and it is difficult to apply to the chain structure

Core code

//Divide the function, select the pivot element, and locate the subscript of the number axis element 
int Partion(int a[], int low, int high){
	int pivot = a[low];//Select the first element as the pivot, or the last element as the pivot
	while(low < high){//Search for pivot position between low and high 
		while(low < high && pivot <= a[high]) high --;
		a[low] = a[high];//Move to the left end smaller than the pivot 
		while(low < high && a[low] <= pivot) low ++;
		a[high] = a[low];//Larger than the pivot moves to the right end 
	}
	a[low] = pivot;//Store the pivot in the final position 
	return low;//Return to the final position where the pivot is stored 
} 

//Quick sort 
void QuickSort(int a[], int low, int high){
	if(low < high){//Recursive jump out condition 
		int pivotpos = Partion(a, low, high);//divide 
		QuickSort(a, low, pivotpos - 1);//Partition left sub table 
		QuickSort(a, pivotpos + 1, high);//Partition right sub table 
	}
}

Compact code

void quick_sort(int q[], int l, int r)
{
    if(l >= r)   return;
    int x = q[l + r >> 1], i = l - 1, j = r + 1;
    while(i < j)
    {
        do i++; while(q[i] < x);
        do j--; while(q[j] > x);
        if(i < j)   swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

Note:

This is the essence of y's lifelong exercise.

Complete code

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx;

//Divide the function, select the pivot element, and locate the subscript of the number axis element 
int Partion(int a[], int low, int high){
	int pivot = a[low];//Select the first element as the pivot 
	while(low < high){//Search for pivot position between low and high 
		while(low < high && pivot <= a[high]) high --;
		a[low] = a[high];//Move to the left end smaller than the pivot 
		while(low < high && a[low] <= pivot) low ++;
		a[high] = a[low];//Larger than the pivot moves to the right end 
	}
	a[low] = pivot;//Store the pivot in the final position 
	return low;//Return to the final position where the pivot is stored 
} 

//Quick sort 
void QuickSort(int a[], int low, int high){
	if(low < high){//Recursive jump out condition 
		int pivotpos = Partion(a, low, high);//divide 
		QuickSort(a, low, pivotpos - 1);//Partition left sub table 
		QuickSort(a, pivotpos + 1, high);//Partition right sub table 
	}
}

int main(){
	//Open file 
	ifstream infile;
	infile.open("D:\\study\\data structure\\Chapter 8 sorting\\in.txt", ios::in);
	
	//Write file 
	ofstream outfile;
	outfile.open("D:\\study\\data structure\\Chapter 8 sorting\\out.txt", ios::out);
	
	if(!infile.is_open()){//Judge whether the file is opened successfully 
		cout << "file open failure!" << endl;
	}
	
	infile >> num;//Number of read elements 
	while(num --){//Copy the elements in the file to the data[1...n] array
		infile >> data[idx ++];
	}
	
	cout << "Element sequence before sorting:" << endl;
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	cout << "use sort Function sorted sequence: " << endl;
	sort(data, data + idx); 
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	QuickSort(data, 0, idx - 1);
	cout << "After using quick sort, the sequence is:" << endl;
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	num = idx, idx = 0, outfile << num << endl;//Write data num and write at end of line \ n 
	while(num --){
		outfile << data[++ idx] << ' ';//Write the sorted data to the file 
	}
	outfile << endl;//Write terminator to end of file \ n 
	
	//Close file 
	infile.close();
	outfile.close();
	return 0;
}

Input data (in.txt)

10
13 69 86 99 59 23 64 32 86 72

Output data (out.txt)

10
13 23 32 59 64 69 72 86 86 99 

Classic examples

Quick sort

Return sorting algorithm directory

6. Merge and sort

Merge sort

Algorithmic thought

Combine two or more ordered sequences into one ordered sequence

Note:

1. The H-th layer of the binary tree has at most 2h-1 nodes. If the tree height is h, it should meet n < = 2h-1, i.e h − 1 = ⌈ l o g 2 n ⌉ h - 1 = \lceil log{_2}n\rceil h − 1 = ⌈ log2 ⌉ n, i.e. number of trips= ⌈ l o g 2 n ⌉ \lceil log{_2}n\rceil ⌈log2​n⌉
2. The time complexity of each merging is O ( n ) O(n) O(n), then the time complexity of the algorithm is O ( n l o g n ) O(nlogn) O(nlogn)
3. Space complexity is O ( n ) O(n) O(n), from auxiliary array

Time complexity

1. Preferably - O ( n l o g n ) O(nlogn) O(nlogn)
2. Worst case - O ( n l o g n ) O(nlogn) O(nlogn)
3. Average - O ( n l o g n ) O(nlogn) O(nlogn)

Note:

Merge sort segmentation subsequence is independent of the initial sequence, so its best, worst and average time complexity are O ( n l o g n ) O(nlogn) O(nlogn)

Demo animation

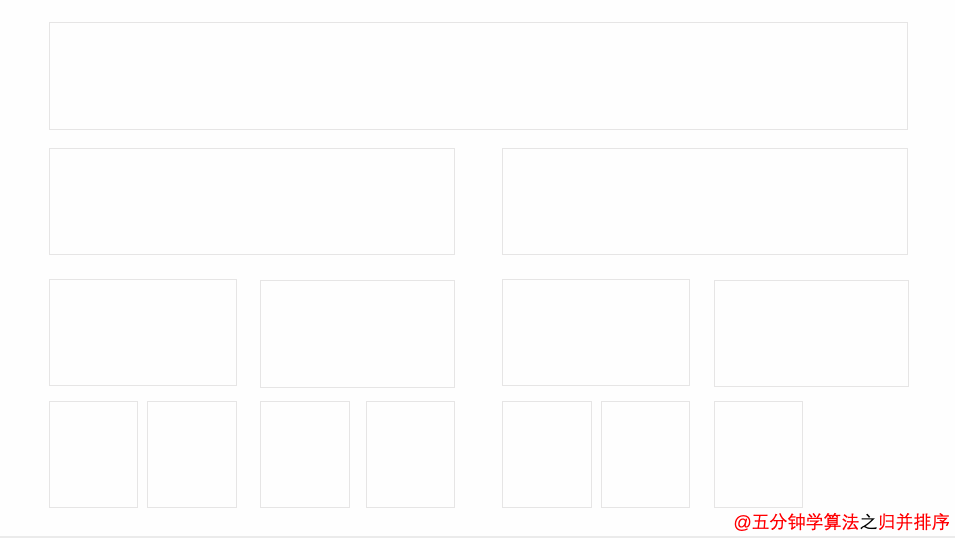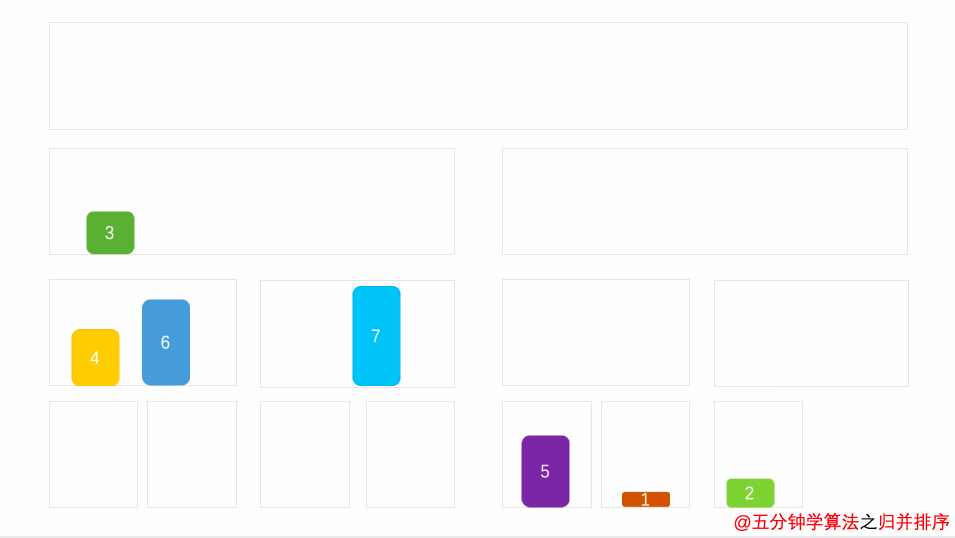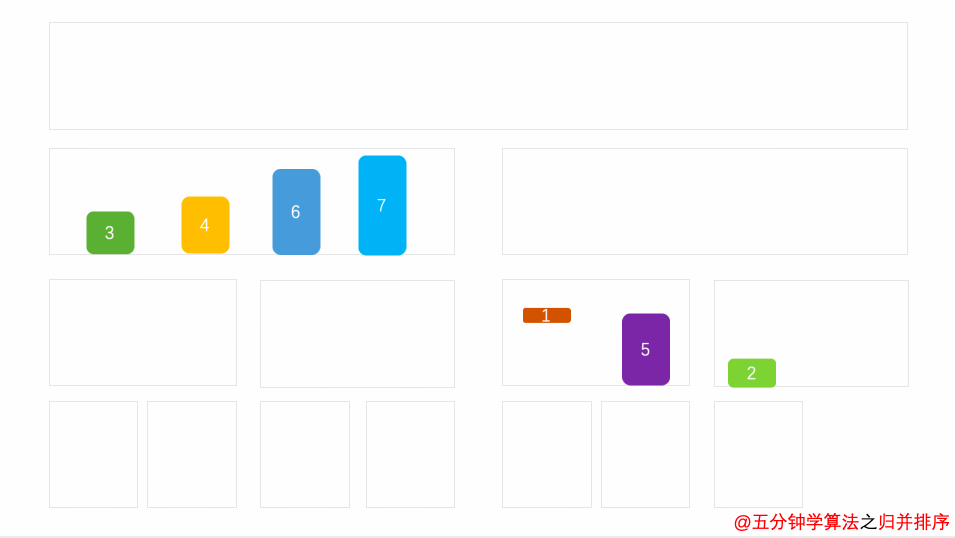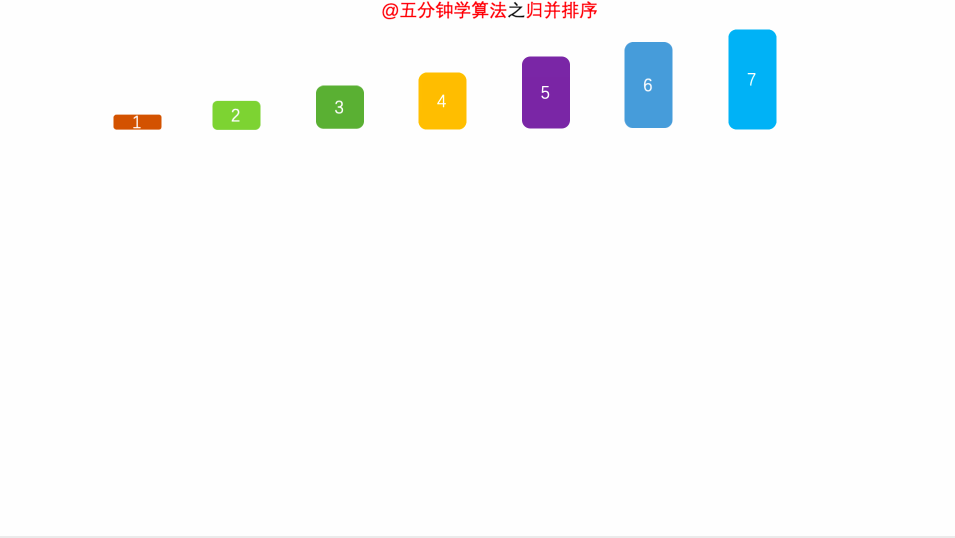
Spatial complexity

An auxiliary array is required---- O ( n ) O(n) O(n)

stability

stable

Applicability

1. Sequence table
2. Linked list

Algorithm characteristics

1. Stable sorting
2. It can be used for sequential structure and chain structure. Using the chain structure does not need additional storage space, but the corresponding recursive work stack still needs to be opened up in the recursive implementation.
3. In general, for n n n elements k k Number of times to sort when k-way merging sorting m m m satisfied k m = n k^m = n km=n, thus m = l o g k n m = log{_k}n m=logk n, taking into account m m m is an integer, so m = ⌈ l o g k n ⌉ m = \lceil log{_k}n\rceil m=⌈logk​n⌉

Core code

//A [low... Mid] and a [mid + 1... High] are ordered respectively and merged 
void Merge(int a[], int low, int mid, int high){
	int k = low;
	int i = low, j = mid + 1;//Left and right header elements 
	
	//Copy array a data to array b 
	for(int i = low; i <= high; i ++) b[i] = a[i];
	
	//Merge a [low... Mid] and a [mid + 1... High]
	while(i <= mid && j <= high){ 
		if(b[i] < b[j]) a[k ++] = b[i ++];
		else a[k ++] = b[j ++];
	}
	
	while(i <= mid) a[k ++] = b[i ++];//Array a has been enumerated 
	while(j <= high) a[k ++] = b[j ++];//b array has been enumerated
}  

// Merge sort 
void MergeSort(int a[], int low, int high){//a[low ...high]
	if(low < high){
		int mid = low + high >> 1;//Divide from the middle 
		MergeSort(a, low, mid);//Merge and sort the left half 
		MergeSort(a, mid + 1, high);//Merge and sort the left half 
		Merge(a, low, mid, high);//Merge 
	}
}

Complete code

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx, b[N];

//A [low... Mid] and a [mid + 1... High] are ordered respectively and merged 
void Merge(int a[], int low, int mid, int high){
	int k = low;
	int i = low, j = mid + 1;//Left and right header elements 
	
	//Copy array a data to array b 
	for(int i = low; i <= high; i ++) b[i] = a[i];
	
	//Merge a [low... Mid] and a [mid + 1... High]
	while(i <= mid && j <= high){ 
		if(b[i] < b[j]) a[k ++] = b[i ++];
		else a[k ++] = b[j ++];
	}
	
	while(i <= mid) a[k ++] = b[i ++];//Array a has been enumerated 
	while(j <= high) a[k ++] = b[j ++];//b array has been enumerated
}  

// Merge sort 
void MergeSort(int a[], int low, int high){//a[low ...high]
	if(low < high){
		int mid = low + high >> 1;//Divide from the middle 
		MergeSort(a, low, mid);//Merge and sort the left half 
		MergeSort(a, mid + 1, high);//Merge and sort the left half 
		Merge(a, low, mid, high);//Merge 
	}
}

int main(){
	//Open file 
	ifstream infile;
	infile.open("D:\\study\\data structure\\Chapter 8 sorting\\in.txt", ios::in);
	
	//Write file 
	ofstream outfile;
	outfile.open("D:\\study\\data structure\\Chapter 8 sorting\\out.txt", ios::out);
	
	if(!infile.is_open()){//Judge whether the file is opened successfully 
		cout << "file open failure!" << endl;
	}
	
	infile >> num;//Number of read elements 
	while(num --){//Copy the elements in the file to the data[1...n] array
		infile >> data[idx ++];
	}
	
	cout << "Element sequence before sorting:" << endl;
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	cout << "use sort Function sorted sequence: " << endl;
	sort(data, data + idx ); //Sort sort interval left closed right open 
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	MergeSort(data, 0, idx - 1);
	cout << "After using heap sorting, the sequence is:" << endl;
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	num = idx, idx = 0, outfile << num << endl;//Write data num and write at end of line \ n 
	while(num --){
		outfile << data[++ idx] << ' ';//Write the sorted data to the file 
	}
	outfile << endl;//Write terminator to end of file \ n 
	
	//Close file 
	infile.close();
	outfile.close();
	return 0;
}

Input data (in.txt)

10
13 69 86 99 59 23 64 32 86 72

Output data (out.txt)

10
13 23 32 59 64 69 72 86 86 99 

Return sorting algorithm directory

7. Simple selection and sorting

Simple selection sort

Algorithmic thought

In each row, select the element with the smallest keyword from the elements to be arranged and add it to the ordered sequence

Note:

Simple selection sorting has nothing to do with the initial state of the sequence, but only with the number of elements of the sequence

Time complexity

1. Preferably - O ( n 2 ) O(n^2) O(n2)
2. Worst case - O ( n 2 ) O(n^2) O(n2)
3. Average - O ( n 2 ) O(n^2) O(n2)

Demo animation

Spatial complexity

Use only one temporary variable min - O ( 1 ) O(1) O(1)

stability

instable

Applicability

1. Sequence table
2. Linked list

Algorithm characteristics

1. Unstable, but changing the strategy can write a selective sorting algorithm that does not produce "unstable phenomenon"
2. Can be used for chained storage structures
3. The number of moves is less. When each record occupies more space, this method is faster than direct insertion sorting
4. The main operation of selecting sorting is keyword comparison. Therefore, the improvement of this algorithm should be considered from reducing the "comparison times"

Core code

//Swap two elements 
void swap(int &a, int &b){
	int temp = a;
	a = b;
	b = temp;
}

//Select sort 
void SelectSort(int a[], int n){
	for(int i = 0; i < n; i ++){
		int min = i;//min record the subscript of the lowest element 
		for(int j = i; j < n; j ++){
			if(a[j] < a[min]) min = j;
		}
		if(min != i) swap(a[i], a[min]);//Swap two values 
	}
}

Complete code

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx;

//Swap two elements 
void swap(int &a, int &b){
	int temp = a;
	a = b;
	b = temp;
}

//Select sort 
void SelectSort(int a[], int n){
	for(int i = 0; i < n; i ++){
		int min = i;//min record the subscript of the lowest element 
		for(int j = i; j < n; j ++){
			if(a[j] < a[min]) min = j;
		}
		if(min != i) swap(a[i], a[min]);//Swap two values 
	}
}

int main(){
	//Open file 
	ifstream infile;
	infile.open("D:\\study\\data structure\\Chapter 8 sorting\\in.txt", ios::in);
	
	//Write file 
	ofstream outfile;
	outfile.open("D:\\study\\data structure\\Chapter 8 sorting\\out.txt", ios::out);
	
	if(!infile.is_open()){//Judge whether the file is opened successfully 
		cout << "file open failure!" << endl;
	}
	
	infile >> num;//Number of read elements 
	while(num --){//Copy the elements in the file to the data[1...n] array
		infile >> data[idx ++];
	}
	
	cout << "Element sequence before sorting:" << endl;
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	cout << "use sort Function sorted sequence: " << endl;
	sort(data, data + idx); 
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	SelectSort(data, idx);
	cout << "After sorting by selection, the sequence is:" << endl;
	for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;
	
	num = idx, idx = 0, outfile << num << endl;//Write data num and write at end of line \ n 
	while(num --){
		outfile << data[++ idx] << ' ';//Write the sorted data to the file 
	}
	outfile << endl;//Write terminator to end of file \ n 
	
	//Close file 
	infile.close();
	outfile.close();
	return 0;
}

Input data (in.txt)

10
13 69 86 99 59 23 64 32 86 72

Output data (out.txt)

10
13 23 32 59 64 69 72 86 86 99 

Return sorting algorithm directory

8. Heap sorting

Heap sort

Algorithmic thought

In each pass, the top element of the heap is added to the ordered subsequence (exchanged with the last element in the sequence of elements to be arranged), and the sequence to be arranged is adjusted to the large root heap again (that is, the small element "falls").

Note:

1. Heap sorting based on "large root heap" results in an incremental sequence
2. For each "falling" layer of a node, you only need to compare keywords twice at most
3. If the tree height is h and a node is in the i-th layer, it only needs to "fall" the h - i layer at most to adjust the node downward, and the keyword comparison times shall not exceed 2(h - i)
4. Complete binary tree with n nodes, tree height h = ⌊ l o g 2 n ⌋ + 1 h = \lfloor log{_2}n \rfloor + 1 h=⌊log2​n⌋+1

Time complexity

1. Preferably - O ( n l o g n ) O(nlogn) O(nlogn)
2. Worst case - O ( n l o g n ) O(nlogn) O(nlogn)
3. Average - O ( n l o g n ) O(nlogn) O(nlogn)

Note: time complexity = O(n) + O(nlog_2n) = O(nlogn)

Demo animation

Spatial complexity

O ( 1 ) O(1) O(1)

stability

instable

Applicability

Applies only to sequence tables

Algorithm characteristics

1. Unstable sorting
2. It can only be used for sequential structure, not chain structure
3. The number of comparisons required for initial reactor building is relatively large. Therefore, when the number of records is small, it should not be used. When there are many records, it is more efficient.

Core code

1. Idea of building large root pile

Check all non terminal nodes to see if they meet the requirements of large root heap. If not, adjust them:

1. Check whether the current node satisfies the root > = left and right. If not, exchange the current node with an older child
2. If the element exchange destroys the next level of heap, continue to adjust downward in the same way (small elements keep "falling")

//Adjust the tree with k as the root node to a large root heap 
void HeadAdjust(int a[], int k, int len){//Note: except for node k, other nodes have been ordered 
	a[0] = a[k];//a[0] temporary child tree root node 
	for(int i = 2 * k; i <= len; i *= 2){//Filter along larger child nodes 
		if(i < len && a[i] < a[i + 1]) i ++;//i is the subscript of the larger child node (i < len indicates that k has a right child) 
		if(a[0] >= a[i]) break;//End of filtering 
		else{
			a[k] = a[i];//Recursive processing of child nodes 
			k = i;
		}
	}
	a[k] = a[0];
}

//Time complexity of building large root heap -- O(n)  
void BuildHeap(int a[], int len){//Build the heap from bottom to top, starting from the root node of the last leaf node 
	for(int i = len / 2; i > 0; i --){//Process all non terminal nodes 
		HeadAdjust(a, i , len);
	}
}//The comparison times of keywords in heap building process shall not exceed 4N (theorem) 

2. Heap sorting idea

Each time, the top element of the heap is added to the ordered subsequence (exchanged with the last element in the to be arranged), and the to be arranged sequence is adjusted to the large root heap again (small elements keep "falling")

//Complete logic for heap sorting 
void HeapSort(int a[], int len){
	BuildHeap(a, len);//Build up O(n) 
	for(int i = len; i > 1; i --){//From post processing to forward processing, n-1 exchanges and adjustments are made in total 
		swap(a[i], a[1]);//Swap the top element (maximum element) with the bottom element 
		HeadAdjust(a, 1, i - 1);//Adjust the remaining elements to be queued to the heap 
	}
}//The time complexity of each trip shall not exceed o (H) = O (logn), n-1 trips in total 

Complete code

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx;

//Adjust the tree with k as the root node to a large root heap 
void HeadAdjust(int a[], int k, int len){//Note: except for node k, other nodes have been ordered 
	a[0] = a[k];//a[0] temporary child tree root node 
	for(int i = 2 * k; i <= len; i *= 2){//Filter along larger child nodes 
		if(i < len && a[i] < a[i + 1]) i ++;//i is the subscript of the larger child node (i < len indicates that k has a right child) 
		if(a[0] >= a[i]) break;//End of filtering 
		else{
			a[k] = a[i];//Recursive processing of child nodes 
			k = i;
		}
	}
	a[k] = a[0];
}

//Time complexity of building large root heap -- O(n)  
void BuildHeap(int a[], int len){//Build the heap from bottom to top, starting from the root node of the last leaf node 
	for(int i = len / 2; i > 0; i --){//Process all non terminal nodes 
		HeadAdjust(a, i , len);
	}
}//The comparison times of keywords in heap building process shall not exceed 4N (theorem) 

//Complete logic for heap sorting 
void HeapSort(int a[], int len){
	BuildHeap(a, len);//Build up O(n) 
	for(int i = len; i > 1; i --){//From post processing to forward processing, n-1 exchanges and adjustments are made in total 
		swap(a[i], a[1]);//Swap the top element (maximum element) with the bottom element 
		HeadAdjust(a, 1, i - 1);//Adjust the remaining elements to be queued to the heap 
	}
}//The time complexity of each trip shall not exceed o (H) = O (logn), n-1 trips in total 

int main(){
	//Open file 
	ifstream infile;
	infile.open("D:\\study\\data structure\\Chapter 8 sorting\\in.txt", ios::in);
	
	//Write file 
	ofstream outfile;
	outfile.open("D:\\study\\data structure\\Chapter 8 sorting\\out.txt", ios::out);
	
	if(!infile.is_open()){//Judge whether the file is opened successfully 
		cout << "file open failure!" << endl;
	}
	
	infile >> num;//Number of read elements 
	while(num --){//Copy the elements in the file to the data[1...n] array
		infile >> data[++ idx];
	}
	
	cout << "Element sequence before sorting:" << endl;
	for(int i = 1; i <= idx; i ++) cout << data[i] << ' '; cout << endl;
	
	cout << "use sort Function sorted sequence: " << endl;
	sort(data + 1, data + 1 + idx); 
	for(int i = 1; i <= idx; i ++) cout << data[i] << ' '; cout << endl;
	
	HeapSort(data, idx);
	cout << "After using heap sorting, the sequence is:" << endl;
	for(int i = 1; i <= idx; i ++) cout << data[i] << ' '; cout << endl;
	
	num = idx, idx = 0, outfile << num << endl;//Write data num and write at end of line \ n 
	while(num --){
		outfile << data[++ idx] << ' ';//Write the sorted data to the file 
	}
	outfile << endl;//Write terminator to end of file \ n 
	
	//Close file 
	infile.close();
	outfile.close();
	return 0;
}

Input data (in.txt)

10
13 69 86 99 59 23 64 32 86 72

Output data (out.txt)

10
13 23 32 59 64 69 72 86 86 99 

Return sorting algorithm directory

Sorting comparison list