1, Bubble sorting
1. Algorithm idea:
- Compare adjacent elements. If the first is larger than the second, exchange the two elements.
- Start from the first element and then compare the two adjacent elements successively until the last one is compared, so that the last element is the largest element.
- Again, start from the first element and compare the two adjacent elements in turn. The last element does not participate until the penultimate element is compared, so the penultimate element is the second largest element.
- Repeat the above steps until only the first element and the second element can be compared and compared.
2. Code implementation:
package com.yzd0507.Order;
//Test several classical sorting algorithms
public class Sort {
//1. Bubble sorting from small to large
public void bubbleSort(int[] arr) {
int len = arr.length;
for(int i=0;i<len-1;i++) {
for(int j=0;j<len-1-i;j++) {
if(arr[j]>arr[j+1]) {
int temp = arr[j+1];
arr[j+1]=arr[j];
arr[j]=temp;
}
}
}
//View the output print elements after sorting
for(int k=0;k<len;k++) {
System.out.println(arr[k]);
}
}
public static void main(String[] args) {
Sort sort = new Sort();
int[] array= {12,3,2,4,66,32,9,2,43};
sort.bubbleSort(array);
}
}

2, Select sort
1. Algorithm idea
- Find the smallest element in the unordered sequence and put it first in the sorted sequence.
- Find the smallest element in the remaining unordered sequence and put it in the second place in the ordered sequence.
- And so on, until there is only the last unordered element left, and put the element in the last place in the sorted sequence.
2. Code implementation
//2. Select sorting from small to large
public void selectSort(int[] arr) {
int len = arr.length;
for(int i=0;i<len-1;i++) {
int minIndex = i;
for(int j=i;j<len;j++) {
if(arr[j]<arr[minIndex]) {
minIndex = j;
}
}
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
//After sorting, output the sorted array
for(int k=0;k<len;k++) {
System.out.println(arr[k]);
}
}
int[] array= {12,3,2,4,66,32,9,2,43};
sort.selectSort(array);

3, Insert sort
1. Algorithm idea
- Take the first element from the sequence to be sorted as the ordered element.
- Take the second element from the sequence to be sorted, and start the comparison from the last element in the sorted sequence as the current element. If the element to be sorted is smaller than the current element, the current element will be moved back one bit. Then point the current element to the penultimate element in the sorted sequence and re compare until the first element in the sorted sequence is compared or the element to be compared is not less than the current element, and insert the element to be compared into the current position.
- Repeat the above steps until all elements are inserted into the corresponding positions.
2. Code implementation
//3. Insert and sort from small to large
public void insertSort(int[] arr) {
int len = arr.length;
for(int i=0;i<len-1;i++) {
int curIndex=i;//The last subscript of the currently ordered array
int temp = arr[i+1];//Need to insert sorted elements
while(curIndex>=0&&temp<arr[curIndex]) {//Compare until the first element of the sorted sequence, and the element to be inserted is smaller than the element currently compared
arr[curIndex+1]=arr[curIndex]; //Compare from back to front
curIndex--;
}
arr[++curIndex] = temp; //Until the first sorted element is compared or not less than the current element, due to curIndex--
//Index has been shifted to the previous position to be inserted, so you need to insert index+1 first
}
//After sorting, output the sorted array
for(int k=0;k<len;k++) {
System.out.println(arr[k]);
}
}
int[] array= {12,3,2,4,66,32,9,2,43};
sort.insertSort(array);
4, Hill sort
Hill sort is an improved version of direct insertion sort, also known as reduced incremental sort. Hill sorting is to group the sequences according to the increment of subscript, directly insert and sort in each group, then gradually reduce the increment and re insert and sort until the increment is reduced to 1. The whole sequence is divided into 1 group, insert and sort, and the algorithm terminates.
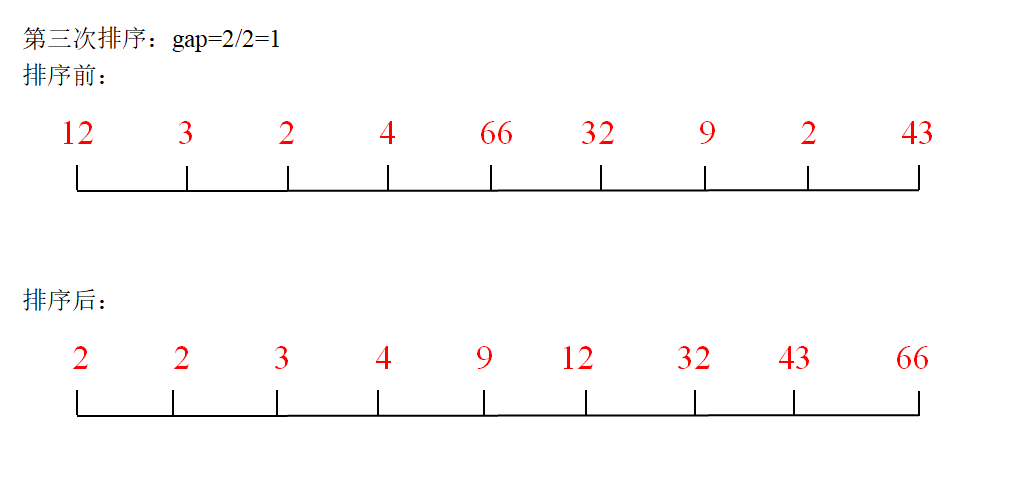
Process, operation 1:



2. Code implementation:
//4. Hill ranking from small to large
public void shellSort(int[] arr) {
int len = arr.length;
for(int gap=len/2;gap>0;gap/=2) {//Gradually reduce the increment
for(int i=0;i<gap;i++) {//Each packet i is the subscript of each packet header
//Insert sort j into the group to index each group of grouped elements to prevent the array index from crossing the boundary
for(int j=i;j<len&&j+gap<len;j=j+gap) {
int temp = arr[j+gap];//Currently need to insert sorted elements
int curIndex=j;//The last subscript of the currently ordered array
while(curIndex>=0&&temp<arr[curIndex]) {//Compare until the first element of the sorted sequence, and the element to be inserted is smaller than the element currently compared
arr[curIndex+gap]=arr[curIndex]; //Compare back and forward moves the current element back
curIndex = curIndex-gap;//Move forward within the current element group
}
curIndex = curIndex+gap; //Find the insertion position of the element that needs to be inserted and sorted
arr[curIndex] = temp;
}
}
}
//After sorting, output the sorted array
for(int k=0;k<len;k++) {
System.out.println(arr[k]);
}
}
int[] array= {12,3,2,4,66,32,9,2,43};
sort.shellSort(array);
5, Merge sort
Merge sort adopts divide and conquer method, combined with recursion.
1. Algorithm description
- The sequence with length n is divided into subsequences with length n/2.
- Split the subsequence again until each subsequence contains only one element.
- The two subsequences are compared from the beginning, and the comparison results are assigned to another array temp. After all the comparison, there will be several elements left in the left and right end sequences. Assign the remaining elements to temp in the original order (the remaining elements have been ordered in the last round of merging), and then copy the data in temp to the subscript position of the left + right subsequence corresponding to the original sequence arr.
- When the merging of the left and right subsequences of the previous level is completed, perform the same operation on the left and right subsequences of the previous level until only two subsequences need to be merged.
2. Operation process:
Merge and sort the sequences: 12, 3, 2, 4, 66, 32, 9, 2 and 43. The green font in the figure is the data of each merging operation, and the red slash of different lengths represents the grouping of different levels.



3. Code implementation
//5. Merge and sort
public void mergeSort(int[] arr) {
int len = arr.length;
sort(arr,0,len-1);//Merge sort
// For (int i = 0; I < arr.length; I + +) {/ / print the sorted array
// System.out.println(arr[i]);
// }
}
public void sort(int[] arr,int left,int right) {
if(right-left<1) {
return;//Recursive exit condition when each element is a group and cannot be split
}
int mid = (left+right)/2;
//Recursively merge and sort the left sequences. arr includes the left and right sequences left, mid, mid+1 and right, which limit the position of operation data
sort(arr,left,mid);//Original left + right original array left sequence start and end Subscripts
//Recursively merge and sort the sequence on the right
sort(arr,mid+1,right);//Original left + right original array right sequence start and end Subscripts
//Merge left and right sequences
merge(arr,left,mid,right);
System.out.print("Data in the original array after performing a merge:");
for(int i=0;i<arr.length;i++) {//Print sorted array
System.out.print(arr[i]+" ");
}
System.out.println(" ");
System.out.println(" ");
}
//Merge the left and right sequences
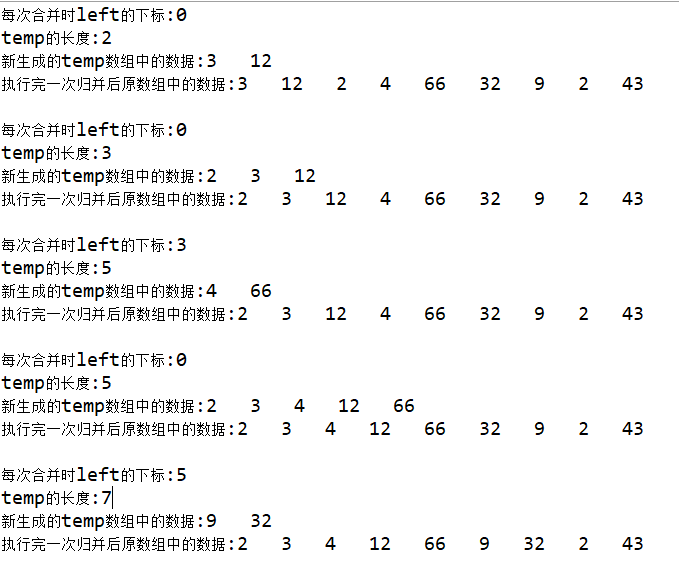
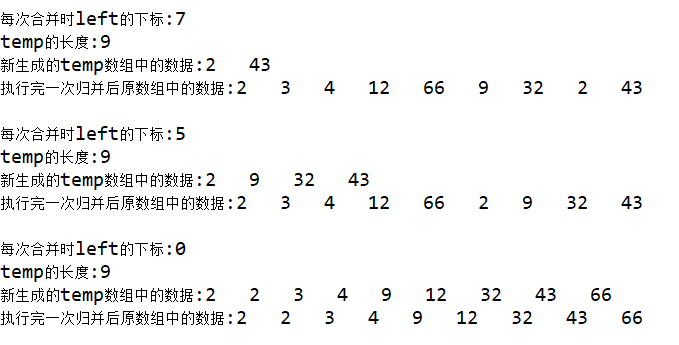
public void merge(int[] arr,int left,int mid,int right) {
//The passed in left, mid and right are the subscripts in the original sequence
System.out.println("At each merge left Subscript of:"+left);
int mid1 = mid+1;
//Left is the starting subscript of the left sequence, mid is the ending subscript of the left sequence, mid2 is the starting subscript of the right sequence, and right is the ending subscript of the right sequence
int[] temp = new int[right+1];//The temporary array used to store the merged sequence creates an appropriate length according to the right position to be merged
System.out.println("temp Length of:"+temp.length);
int index=left;//Subscript of temporary array??? The correct way is not necessarily to start copying from the subscript 0 of the temp array. You can only assign values in some positions, leave other positions empty as the default value 0, and start copying at the position corresponding to the original array at the end of the temp array
//int index=0; //??? The error mode index is left + right. When the right sequence is merged, the index recursively adds the right sequence based on the left sequence
int lstart=left;//Record the subscript of the first element in the left sequence??? Correct way
//int lstart=0;// ??? In the error mode, the middle part of lstart does not start from 0. It is sorted at the corresponding position of each group, and it is not sorted separately
int rstart=mid1;//Record the subscript of the first element in the right sequence
//1. Starting from the initial position of the sequences on the left and right sides, take the smaller value and put it in the temp array. The starting position of the sequence with the value will be moved one bit later, and the sequence without value will remain unchanged
while(lstart<=mid&&rstart<=right) {
if(arr[lstart]<arr[rstart]) {
temp[index]=arr[lstart++];
//System.out.println(temp[index]);
index++;
}else {
temp[index]=arr[rstart++];
//System.out.println(temp[index]);
index++;
}
}
//2. After all the sequences on one side are taken, directly copy the remaining data on the other side to the temp array (the sequence on each side has been taken in the last round of recursion)
//Only one of the following two if will execute
while(lstart<=mid) {
temp[index++]=arr[lstart++];
//System.out.println(temp[index]);
}
while(rstart<=right) {
temp[index++]=arr[rstart++];
//System.out.println(temp[index]);
}
//3. Copy data from temp to arr????? Error mode: only the ARR elements that have performed the merge operation are updated each time. The ARR elements that have not performed the merge operation are not changed, and the operation is not necessarily from 0
// //When the merge method is called recursively on the right, the operation is based on the left. The generated temp length is left + right, so the starting subscript of u is left (the left of the right sequence)
// for(int u=0;u<temp.length;u++) {
// arr[u]=temp[u];
//
// //System.out.print(temp[u]+" ");
// }
System.out.print("Newly generated temp Data in array:");
//3. Copy the data in temp to arr??? Correct way
for(int u=left;u<temp.length;u++) {//When creating the length of temp array and initializing index, copy from the left position
arr[u]=temp[u];
System.out.print(temp[u]+" ");
}
System.out.println(" ");
}
int[] array= {12,3,2,4,66,32,9,2,43};
sort.mergeSort(array);
Output result diagram:
Complete code of the above algorithm:
Baidu online disk extraction code: g903