catalogue

Write a callable function. Each call can increase the value of num by 1

Determine the prime number between 100 and 200

Judge leap years between 1000 and 2000

Using dichotomy to find ordered arrays

Write a callable function. Each call can increase the value of num by 1

Tip: it is necessary to use address transfer call (pointer) (if necessary, you can go to the first chapter of my home page to understand the difference between value transfer call and address transfer call)

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

void Add (int *p)
{
	(*p)++; //It cannot be written as * p + +, because + + only works on p
}

int main()
{
	int num = 0;

	Add(&num);
	printf("num=%d\n", num);

	Add(&num);
	printf("num=%d\n", num);

	Add(&num);
	printf("num=%d\n", num);

	return 0;
}

The result is:

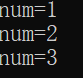
Determine the prime number between 100 and 200

Tip: prime numbers are also called prime numbers. A natural number greater than 1 that cannot be divided by other natural numbers except 1 and itself is called a prime number. According to its definition, we can think of using the "%" in C language to take the remainder. The remainder is not 0. This number is a prime number, the remainder is 0, and this number is not a prime number.

The answer is as follows:

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

int sushu (int i)
{
	int  j = 0;
	for (j = 2; j < i ; j++)
	{
		if ( i%j == 0)
		{
			return 0;
		}
	}
	return 1;

}


int main()
{
	int i = 0;
	for (i = 100; i <= 200; i++)
	{
		if (sushu(i) == 1)
		{
			printf("%d  ", i);
		}
	}

	return 0;
}

The results are:

Judge leap years between 1000 and 2000

Tip: every four years is moist, every hundred years is not moist, and every 400 years is moist again.

The answer is as follows:

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

int runnian(int year)
{
	if ( ( (year % 4 == 0) && ( year % 100 != 0) ) || year % 400 == 0)
	{
		return 1;
	}
	return 0;
}

int main()
{
	int year = 0;
	for (year = 1000; year <= 2000; year++)
	{
		if (runnian(year) == 1)
			printf("%d  ", year);
	}
	return 0;
}

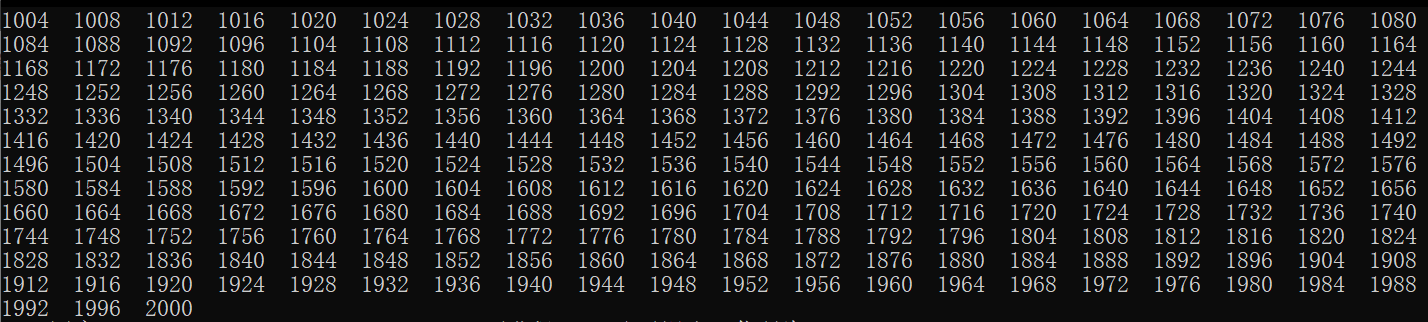
The results are:  

Using dichotomy to find ordered arrays

Dichotomy lookup definition:

The basic idea of binary search is to divide n elements into roughly equal two parts, compare a [n/2] with X, if x=a [n/2], find X and the algorithm stops; If x < a [n/2], continue searching for X in the left half of array A. if x > a [n/2], search for X in the right half of array a. the time complexity is the number of while loops.

For example, the following figure shows an ordered array from 1 to 10, with subscripts from 0 to 9 at the bottom. We use subscripts to find our numbers. When we want to find the number 7, the left subscript is 0, the right subscript is 9, 0 + 9 / 2 is 4.5, the integer is 4, and the subscript 4 corresponds to the number 5. At this time, we find that 5 is smaller than the number we want to find, so we can raise the lower left table to the lower table 4 + 1 = 5, and the right subscript is 9. In this process, we cycle until we find the number 7.

  Then we can write the answer:

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

int serch (int arr[ ], int k, int sz)
{
	int left = 0;
	int right = sz - 1;
	while (left <= right)
	{
		int mid = (left + right) / 2;
		if (arr[mid] < k)
		{
			left = mid + 1;
		}
	 else if (arr[mid] > k)
		{
			right = mid - 1;
		}
	 else
		{
			return mid;
		}
	  }
	return -1;
}

int main()
{
	int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
	int k = 7;
	int sz = sizeof(arr) / sizeof(arr[0]);
	int ret = serch(arr, k, sz);
	if (ret == -1)
	{
		printf("The specified number cannot be found\n");
	}
	else 
	{
		printf("Yes, the subscript is:%d\n", ret);
	}
	return 0;
}

The results are:

The above is the classic beginner function problem! If you like it, you can give it a little praise! Thanks for browsing!

(if there is any problem, please point it out and I will correct it in time!!)