Prepare training and test data sets
As soon as I came up, I found that the dataset could not be found. After searching, I finally found the dataset in another package.
# install.packages("C50")
# library(C50)
# data('churn', package = 'C50')
# install.packages("modeldata")
# https://stackoverflow.com/questions/60506936/data-set-churn-not-found-in-package-c50
library(modeldata)
data(mlc_churn)
churn <- mlc_churn
# 7: 3-point training and test set
set.seed(2)
ind <- sample(2,nrow(churnTrain),replace = TRUE,
prob = c(0.7,0.3))
trainset <- churnTrain[ind==1,]
testset <- churnTrain[ind==2,]
This data set is slightly different from that in the book, but it should contain more relationships. There are more samples of this data, which should not be affected. Extension: split function completes the division of training and testing
split.data <- function(data, p= 0.7, s= 666){
set.seed(s)
index <- sample(1:dim(data)[1])
train <- data[index[1:floor(dim(data)[1]*p)],]
test <- data[index[((ceiling(dim(data)[1]*p))+1):dim(data)[1]],]
return(list(train=train,test=test))
}
li <- split.data(churnTrain)
Using recursive segmentation tree to establish classification model
Recursion and segmentation are two steps of this algorithm. CP is a cost complexity parameter. The disadvantage of decision tree algorithm is that it is easy to produce deviation and over adaptation. Conditional reasoning tree can overcome deviation, and over adaptation can be solved by random forest method or tree pruning.
library(rpart) churn.rp <- rpart(churn~., data=trainset) plotcp(churn.rp) summary(churn.rp)
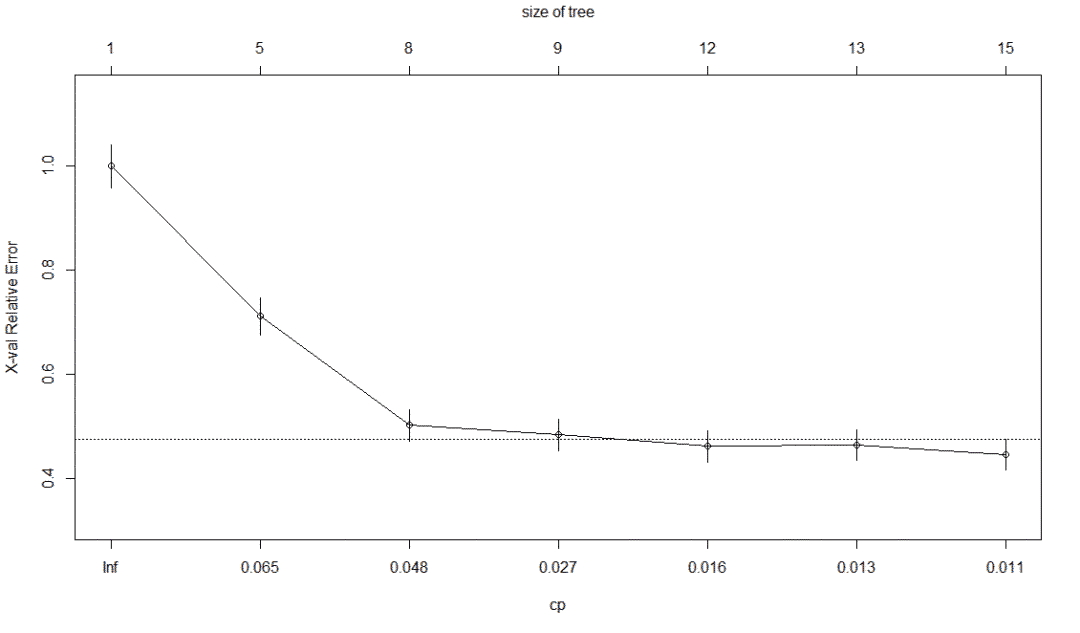
5.4 recursive split tree visualization
plot and text functions draw a classification tree.
plot(churn.rp, margin = 0.1) # frame text(churn.rp, all = TRUE, use.n = TRUE) # use.n number of actual observations per category # Change the parameters to adjust the display results plot(churn.rp, uniform = TRUE, branch = 0.6, margin = 0.1) # brach setting shoudler text(churn.rp,all = TRUE, use.n = TRUE)
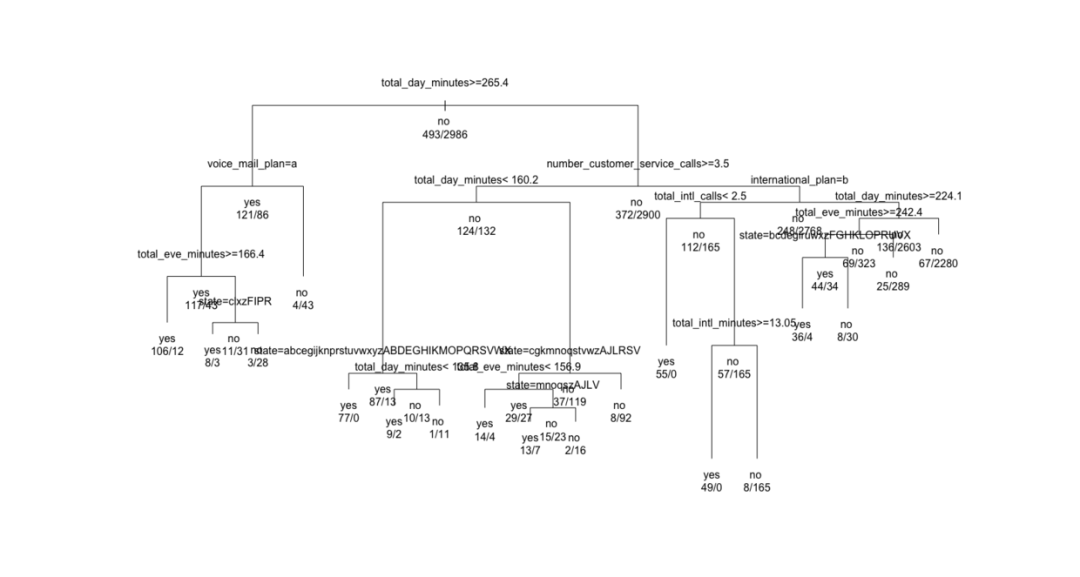
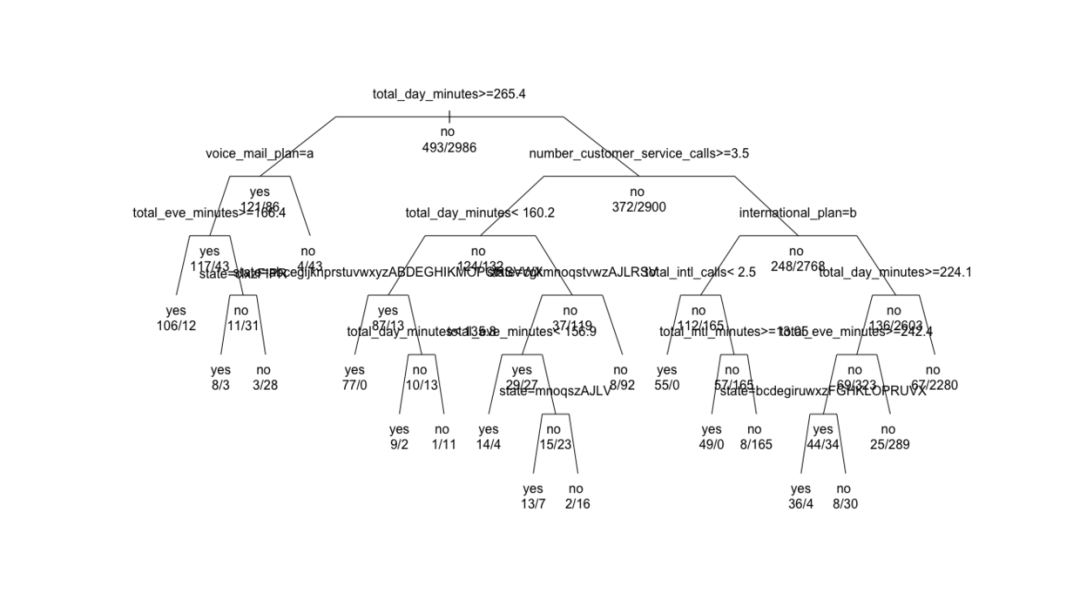
5.5 evaluate the classification ability of recursive split tree
# forecast
predictions <- predict(churn.rp, testset, type = "class")
table(testset$churn, predictions)
# #############
predictions
yes no
yes 133 81
no 29 1278
# Generating confusion matrix
library(caret)
confusionMatrix(table(predictions, testset$churn))
Confusion Matrix and Statistics
# ##############
predictions yes no
yes 133 29
no 81 1278
Accuracy : 0.9277
95% CI : (0.9135, 0.9402)
No Information Rate : 0.8593
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.6671
5.6 recursive split tree pruning
Sometimes, it is necessary to prune the rules with weak classification description ability to avoid over adaptation and improve the prediction accuracy. The cost complexity method is used here.
min(churn.rp$cptable[,"xerror"]) [1] 0.4523327 which.min(churn.rp$cptable[,"xerror"]) 5 5 # Minimum cost complexity parameter churn.cp <- churn.rp$cptable[5,"CP"] churn.cp [1] 0.01014199 # trim prune.tree <- prune(churn.rp, cp=churn.cp) plot(churn.rp, margin = 0.1) text(churn.rp,all = TRUE, use.n = TRUE) # The confusion matrix is slightly lower than that before pruning to avoid over fitting confusionMatrix(table(predictions, testset$churn)) # ################
I don't seem to find much
5.7 establish classification model using conditional reasoning tree
In addition to the traditional rpart decision tree algorithm, conditional inference tree ctree is another commonly used tree based classification algorithm. The recursive partition of data is also realized for non independent variables. The difference is that the conditional reasoning tree selects split variables based on the results of significance measurement rather than the information maximization method. The Gini coefficient is used in rpart, which does not represent the gap between the rich and the poor.
# Conditional reasoning tree library(party) ctree.moddel <- ctree(churn~., data = trainset) ctree.moddel
5.8 conditional reasoning tree visualization
# visualization plot(ctree.moddel) daycharhe.model <- ctree(churn~total_day_charge, data = trainset) plot(daycharhe.model)

Simplify it
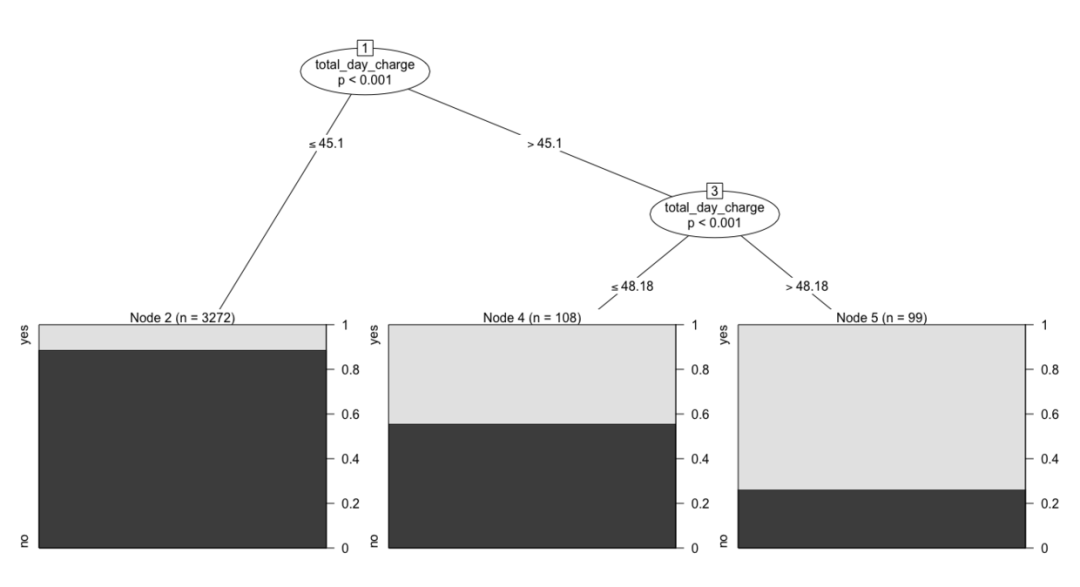
5.9 evaluation and prediction ability
# forecast
> ctree.predict<- predict(ctree.moddel, testset)
> table(ctree.predict, testset$churn)
ctree.predict yes no
yes 139 9
no 75 1298
confusionMatrix(table(ctree.predict, testset$churn))
# #######################
Confusion Matrix and Statistics
ctree.predict yes no
yes 139 9
no 75 1298
Accuracy : 0.9448
95% CI : (0.9321, 0.9557)
No Information Rate : 0.8593
P-Value [Acc > NIR] : < 2.2e-16
# probability
> treeresponse(ctree.moddel, newdata = testset[1:5,])
[[1]]
[1] 0.02715356 0.97284644
[[2]]
[1] 0.06842105 0.93157895
[[3]]
[1] 0.06842105 0.93157895
[[4]]
[1] 0.06842105 0.93157895
[[5]]
[1] 0.02715356 0.97284644
5.10 using k-adjacency classification algorithm
It is a nonparametric inert learning method, does not make any assumptions about the data distribution, and does not require the algorithm to have an explicit learning process.
install.packages("class")
library(class)
levels(trainset$international_plan) = list("0" = "no", "1" = "yes")
levels(trainset$voice_mail_plan) = list("0" = "no", "1" = "yes")
levels(testset$international_plan) = list("0" = "no", "1" = "yes")
levels(testset$voice_mail_plan) = list("0" = "no", "1" = "yes")
churn.knn <- knn(trainset[,!names(trainset) %in% c("churn", "area_code", "state" )],
testset[,!names(testset) %in% c("churn", "area_code", "state" )], trainset$churn, k=3)
summary(churn.knn)
plot(churn.knn)
library(caret)
confusionMatrix(table(testset$churn,churn.knn))
# ########################
Confusion Matrix and Statistics
churn.knn
yes no
yes 76 138
no 46 1261
Accuracy : 0.879
95% CI : (0.8616, 0.895)
No Information Rate : 0.9198
P-Value [Acc > NIR] : 1
Kappa : 0.3901
knn algorithm uses similarity distance to train and classify. For example, Euclidean distance or Manhattan distance, k=1, will allocate samples to the nearest category. If K is small, it may be over fitting, too large or low fitting, and a suitable value can be obtained by cross test. The advantage is that the learning cost is 0, there is no need to assume distribution, and any type of data can be processed; The disadvantage is that it is difficult to understand, the data set is large, the calculation cost is very high, and the dimension of high-dimensional data must be reduced first. Character type data shall be processed into integer first, and k=3 shall be allocated to the last three clusters. kknn package can provide weighted k-nearest neighbor algorithm, regression and clustering.
5.11 using logistic regression
It is an algorithm based on probability and statistics. The logit function can be executed. The glm family specified as binomial is also a logical regression algorithm.
# logistic
fit <- glm(churn~., data = trainset,family = binomial)
summary(fit)
# Remove non significant variables
fit <- glm(churn~international_plan + voice_mail_plan + total_intl_calls + number_customer_service_calls , data = trainset,family = binomial)
summary(fit)
pred <- predict(fit, testset, type = "response")
pred <- predict(fit, testset, type = "response")
Class <- pred > .5
summary(Class)
Mode FALSE TRUE
logical 44 1477
pred_class <- churn.mod
pred_class[pred <=.5] = 1- pred_class[pred<=.5]
ctb <- table(churn.mod, pred_class)
ctb
# ###########
pred_class
churn.mod 0 1
0 1287 20
1 24 190
confusionMatrix(ctb)
Confusion Matrix and Statistics
pred_class
churn.mod 0 1
0 1287 20
1 24 190
Accuracy : 0.9711
95% CI : (0.9614, 0.9789)
No Information Rate : 0.8619
P-Value [Acc > NIR] : <2e-16
Kappa : 0.8794
Logistic regression is easy to understand, directly outputs probability and confidence interval, and can quickly merge new data sets and update classification models. The disadvantage is that it cannot deal with multicollinearity, and the explanatory variables must be linear independent.
5.12 using naive Bayesian classification algorithm
It is also a probability based classifier, which assumes that the sample attributes are independent of each other.
library(e1071)
classifer <- naiveBayes(trainset[,!names(trainset) %in% c("churn")], trainset$churn)
classifer
# ##############
Naive Bayes Classifier for Discrete Predictors
Call:
naiveBayes.default(x = trainset[, !names(trainset) %in% c("churn")],
y = trainset$churn)
# ###############
A-priori probabilities:
trainset$churn
yes no
0.1417074 0.8582926
bayes.table <- table(predict(classifer, testset[,!names(trainset) %in% c("churn")]), testset$churn)
bayes.table
# #############
yes no
yes 104 52
no 110 1255
library(caret)
confusionMatrix(bayes.table)
Confusion Matrix and Statistics
# ############
yes no
yes 104 52
no 110 1255
Accuracy : 0.8935
95% CI : (0.8769, 0.9086)
No Information Rate : 0.8593
P-Value [Acc > NIR] : 4.220e-05
Kappa : 0.5032
Classification evaluation is based on the above routine. The naive Yess algorithm assumes that the characteristic variables are conditionally independent, with relatively simple advantages and direct application. It is suitable for training data sets with small-scale trees and possible missing or data noise. The disadvantage is that the above conditions are independent and equally important, which is difficult to achieve in the real world. To summarize this chapter, see the following pictures:
