[clock out algorithm] 12. Analysis of integer to Roman numeral algorithm

1, Title

1. Algorithm topic

Convert the entered integer to Roman numerals

Title Link:
Source: LeetCode

Link: https://leetcode-cn.com/problems/integer-to-roman/

2. Title Description

Roman numerals contain the following seven characters: I, V, X, L, C, D and M.

character	numerical value
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

For example, the Roman numeral 2 is written as II, which is two parallel ones. 12 is written as XII, which is X + II. 27 is written as XXVII, which is XX + V + II.

Usually, the small Roman numerals are to the right of the large ones. But there are also special cases. For example, 4 is not written as IIII, but IV. The number 1 is on the left of the number 5, and the number represented is equal to the value 4 obtained by subtracting the decimal 1 from the large number 5. Similarly, the number 9 is represented as IX. This special rule applies only to the following six cases:

I can be placed to the left of V (5) and X (10) to represent 4 and 9.
X can be placed to the left of L (50) and C (100) to represent 40 and 90.
C can be placed to the left of D (500) and M (1000) to represent 400 and 900.
Give you an integer and convert it to Roman numerals.

Example 1:
Input: num = 3
 Output:"III"

Example 2:
Input: num = 48
 Output:"XLVIII"
analysis: XL = 40 , V = 5 , III = 3

Example 3:
Input: num = 4994
 Output:"MIVCMXCIV"
Resolution: MIV = 4000 , CM = 900 , XC = 90 , IV = 4

2, Problem solving

1. Train of thought analysis

Roman numerals are composed of 7 symbols, and each symbol corresponds to a specific value. According to the subtraction rules, 6 additional composite symbols are given, a total of 13 unique symbols, as shown in the following figure:

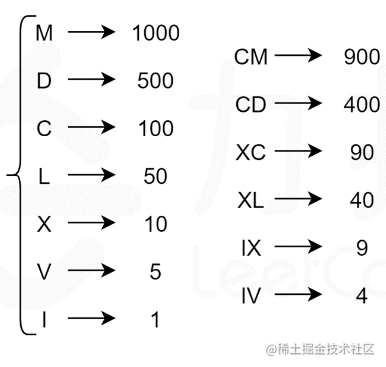
The key to this problem is to select the largest symbol value as possible when converting integers into Roman numerals, such as 140. The maximum symbol value can be C = 100, and then 40. The maximum symbol value XL = 40.

2. Code implementation

Violent solution:

This idea is relatively simple, because when an integer is converted to Roman numerals, the digits in each digit can be processed separately. Using modular operation and trigger operation, the digits in each digit can be obtained, and then combined with the digits in Roman numerals.

public class Solution 
{
    public string IntToRoman(int num) 
    {
        string[] M = { "", "M", "MM", "MMM" }; // 1000，2000，3000
        string[] C = { "", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM" }; // 100~900
        string[] X = { "", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC" }; // 10~90
        string[] I = { "", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX" }; // 1~9
        return M[num / 1000] + C[(num % 1000) / 100] + X[(num % 100) / 10] + I[num % 10];
    }
}

Greedy Algorithm

Greedy rule: try to use the largest number every time, such as 2118. Try to select the largest number every time, that is, 2000100, 10, 8, and you will get the correct result: MMCXVIII.

public class Solution 
{
    public string IntToRoman(int num) 
    {
        int[] values = { 1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1 };
        string[] rom = { "M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I" };
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < values.Length; i++)
        {
            while (num >= values[i])
            {
                sb.Append(rom[i]);
                num -= values[i];
            }
        }
        return sb.ToString();
    }
}

3. Time complexity

Time complexity: O(1)

The amount of calculation is independent of the size of the input number.

Space complexity: O(1)

The amount of calculation is independent of the size of the input number.

3, Summary

This problem uses two solutions to solve it. Of course, there are more solutions. We should think more.

Greedy rule of greedy algorithm: try to use the maximum number each time. Similar to the principle of converting integers to Roman numerals to larger numbers, fewer characters are more convenient for communication and use. This should also be the original intention of people designing Roman numerals.

Keywords: Algorithm

Added by terfle on Mon, 25 Oct 2021 08:51:07 +0300

Programming VIP