preface
I use it to record the title of the book written by the boss of my brush code Capriccio (that is, Carl). If there is a self search code Capriccio that I want to learn together, I can.
This is an array.
The number at the beginning of the title is the serial number of the title in LeetCode.
Array article
704. Binary search:

This is a very classic two-point search question, which is more water. Those who understand two points can basically write it directly. I wrote my own solution directly:
class Solution {
public int search(int[] nums, int target) {
int left = 0; //Defines a left pointer to the starting point element of the array
int right = nums.length-1; //Defines a right pointer to the end element of the array
int mid = (left+right)/2; //Middle pointer to the middle element of the array
//Eternal cycle always judge
while(true){
//If the array is not found until it is traversed, the result of - 1 is returned, indicating that it is not found
//Here's a trick. You can't judge left > = right directly,
//Because it is possible that the mid value when the subscript left==right is exactly the value we are looking for
if(left > right) return -1;
//If found, return the subscript directly
if(target == nums[mid]) return mid;
//If the target value is less than the middle value
if(target < nums[mid]){
//Then make the range pointed by the right pointer smaller
right = mid - 1;
}else{
//Then make the range pointed by the left pointer larger
left = mid + 1;
}
//Refresh mid value
mid = (right + left) / 2;
}
}
}
35. Search insertion position

The title is also very simple, and the ideas are all in the code:
class Solution {
public int searchInsert(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
int mid = (left+right) / 2;
while(true){
if(left > right) break;
if(target == nums[mid]) return mid;
if(target < nums[mid]) right = mid - 1;
else left = mid + 1;
mid = (left + right) / 2;
}
//If the target value is not found, follow the above logic
//It will jump out of the loop to execute the following logic
//If the target value is not found, the position where it will be inserted in sequence is returned
int cnt = 0; //Counter, record insertion position
for(int i = 0;i < nums.length;i++){
if(target < nums[i]) return cnt;
cnt++;
}
return nums.length;
}
}
34. Find the first and last position of an element in a sorted array
Idea:
Here, my ideas coincide with the ideas of a recording friend, so I directly copied his ideas, because I felt that what I said was not as good as him.
1. First, binary search target in num array;
2. If binary search fails, binarySearch returns - 1, indicating that there is no target in nums. At this time, searchRange directly returns {- 1, - 1};
3. If the binary search is successful, binarySearch returns a subscript with the value of num as target. Then, slide the pointer left and right to find the interval that meets the meaning of the question
My code implementation is given below, and the comments are clearly written:
class Solution {
public int[] searchRange(int[] nums, int target) {
//This problem is because arrays are arranged in ascending order
//Therefore, if there are target values, these target values must be arranged next to each other
//Then the problem should be easy to solve
//We first use binary search to determine whether we can find the target value
int left = 0;
int right = nums.length - 1;
int mid = (left + right) / 2;
//Create a result array to return results
int[] arr = {-1,-1};
while(true){
if(left > right) return arr; //Not found, directly return - 1, - 1
if(target == nums[mid]){ //If it is found, we will start from the coordinates of the found value and traverse left and right
//This target value exists
//So what we have to do now is
//This is where you start traversing forward and backward
//Find the start and end positions of this value
int i = mid;
while(i+1 < nums.length && target == nums[i+1]){ //The logic to judge whether the array is out of bounds must be in the front. Here is the writing method of short circuit and
//As long as the previous I + 1 < num If length does not meet the conditions, it will jump out directly regardless of the subsequent judgment
//Traverse backward first. When target and num [i] are not equal, exit the loop
i++;
}
//Exit the loop, this is the end position
//The result array assigned to us
arr[1] = i;
//Backward traversal is over, now forward traversal
i = mid; //Refresh i value
while(i-1 >= 0 && target == nums[i-1]){
//Traverse forward again. When target and num [i] are not equal, exit the loop
i--;
}
//Exit the loop, this is the start position
//The result array assigned to us
arr[0] = i;
return arr;
}
if(target < nums[mid]) right = mid - 1;
else left = mid + 1;
mid = (left + right) / 2;
}
}
}
One thing that needs to be paid attention to in this problem is that you must pay attention to the judgment of array crossing the boundary!!!
This kind of mistake is easy to make in many problems. Short circuit and are a good solution.
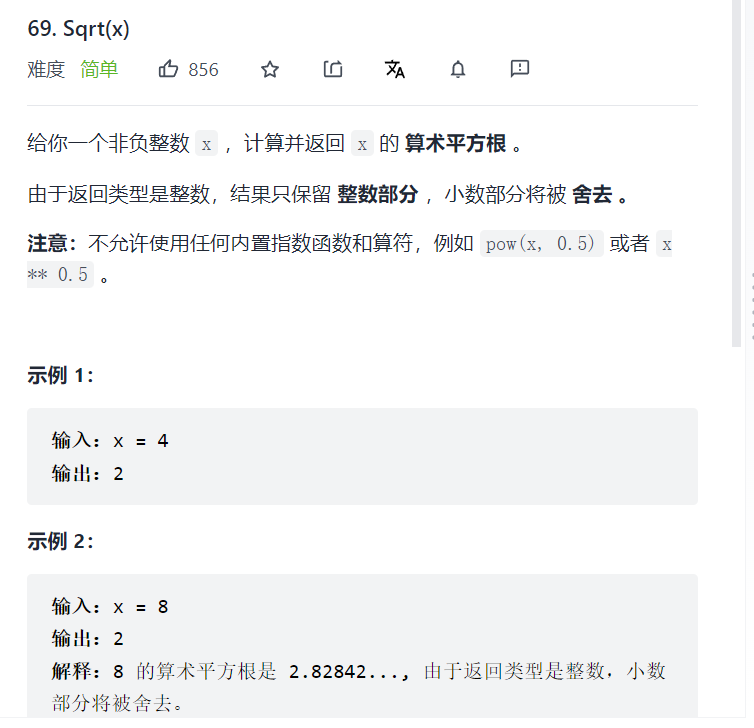
69. Sqrt(x)
Title Description:
Idea:
I carried the idea of a respondent on LeetCode, and I think it's well written.
The square root of integer x must be less than or equal to X;
The square root of all integers except 0 is greater than or equal to 1;
The square root of integer x must be in the range of 1 to X. take the middle number mid in this range and judge whether the square of mid is less than or equal to X. if the square of mid is less than x;
Then, judge whether the square of (mid+1) is greater than x. if the square of (mid+1) is greater than x, then mid is the square root of X;
If the square of mid is less than X and the square of (mid+1) is less than x, the square root of X is larger than mid, and then search the range from mid+1 to X;
If the square of mid is greater than x, the square root of X is less than mid, and then search the range from 1 to mid-1
Then repeat the process in the corresponding range, always taking out the mid in the middle of the range;
The code is as follows:
class Solution {
public int mySqrt(int x) {
//Because the data range is large, in order to avoid overflow, long type is adopted
long left = 0;//Left pointer
long right = x; //Right pointer
long ans = 0; //Record the value of the result
//Binary search, k square is less than or equal to x, this is a mathematical formula
while(left <= right){
long mid = (right + left) / 2;
if(mid*mid <= x){//Meet the conditions
ans = mid; //Assign a result value
left = mid + 1;
}else{
right = mid - 1;
}
}
//The title requires return shaping, indicating that the final result must be within the scope of shaping
//So we don't have to worry about the lack of precision from big to small, just type conversion directly
return (int)ans;
}
}
367. Effective complete square
Title Description:

This question is a variant of the above question. The ideas are the same. You can find the qualified value by binary search:
class Solution {
public boolean isPerfectSquare(int num) {
//A variant of the previous question
//The idea is to use binary search to find out if there is one equal to this value
long left = 0;
long right = num;
while(left <= right){
long mid = (left+right) / 2;
if(mid * mid == num){
return true;
}else if(mid*mid < num){
left = mid + 1;
}else right = mid - 1;
}
return false;
}
}
27. Remove element
Title Description:

Idea:
The idea of double finger needling is hard for me to say. I did it after reading the problem solution. I feel that I have to rely on my own understanding. I should be able to understand the problem solution of others.
Anyway, it's a fast pointer and a slow pointer. Then the fast pointer keeps walking, and the slow pointer only goes under special circumstances. This special case depends on the subject. Finally, you only need to return the value of the slow pointer. Look at the code. It should be better.
class Solution {
public int removeElement(int[] nums, int val) {
//Double finger needling
int slowIndex = 0; //Slow pointer
int fastIndex = 0; //Quick pointer
for(;fastIndex < nums.length;fastIndex++){//Come on, keep going
if(nums[fastIndex] != val){//Under special circumstances, this problem is to put the qualified value into the memory space pointed by the slow pointer (the array is pointed by the subscript)
nums[slowIndex] = nums[fastIndex];
slowIndex++; //If the conditions are met, the slow pointer starts to move
}
}
//Just return the value of the slow pointer
return slowIndex;
}
}
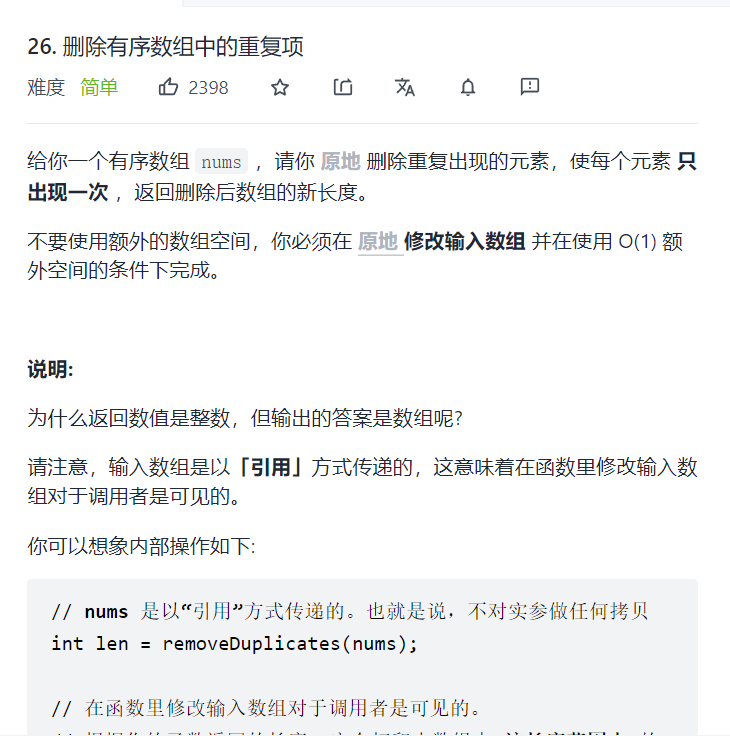
26. Remove duplicates from the sort array
Title Description:
Idea:
First of all, remember that the problem of linear table can generally be solved by double pointer method.
Then, before doing the topic, you must first look at the tips given by the topic. People have said that this array is an ascending array, so the equal values must be next to each other in this array. In that case, we just need to judge whether the array element value pointed to by the fast pointer is equal to the previous array element value to complete the problem. If it is equal, it doesn't matter. Equality means repetition. We can't put it into the array in a sense pointed to by the slow pointer (I have to understand it myself). If it is not equal, it means that it is not repeated, We can put it in, and then let the slow pointer increase automatically to receive the arrival of the next non repeating value:
class Solution {
public int removeDuplicates(int[] nums) {
//This linear problem can generally be solved with double pointers
int slowIndex = 1; //The first value must be, so let's start with the second value
int fastIndex;
for(fastIndex = 1;fastIndex < nums.length;fastIndex++){
if(nums[fastIndex] != nums[fastIndex-1]){//Judge whether the array element value pointed by the fast pointer is equal to the previous array element value each time
nums[slowIndex] = nums[fastIndex];
slowIndex++;
}
}
return slowIndex;
}
}
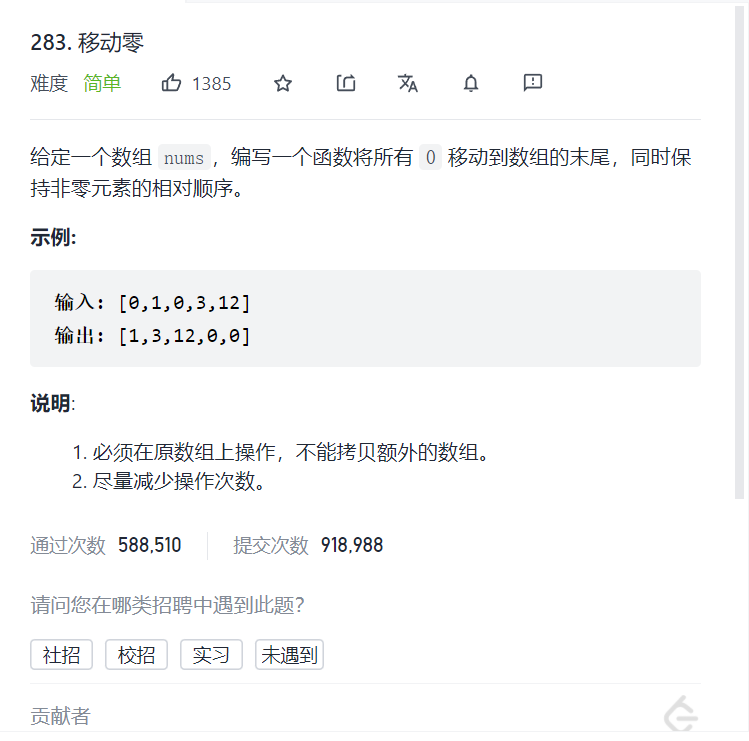
283. Move zero
Title Description:
Idea:
They are all the same type of questions. They are almost the same. I write my ideas in the code and just look at the code.
class Solution {
public void moveZeroes(int[] nums) {
//Old method
//If it is a linear problem, double pointers can generally be solved
int slowIndex = 0;
int fastIndex = 0;
for(;fastIndex<nums.length;fastIndex++){
if(nums[fastIndex] != 0){ //If it is not equal to 0, it is placed in the array pointed to by the slow pointer
nums[slowIndex] = nums[fastIndex];
slowIndex++;
}
}
//After the above processing, the array pointed to by the slowIndex slow pointer must have all the values in the original order
//What we need to do now is to set the element less than the array length after the slow pointer of slowIndex to 0
while(slowIndex < nums.length){
nums[slowIndex] = 0;
slowIndex++;
}
}
}
844. Compare strings with backspace
Title Description:

Idea:
Double finger acupuncture.
You can refer to the problem solution on LeetCode. I have also referred to it before I almost want to understand it. However, I have clear notes at each step of the following code. I should be able to see it clearly with the problem solution ideas on LeetCode.
It's wonderful! In fact, another solution should be simpler, that is, using a stack or something, which will be easier to understand.
class Solution {
public boolean backspaceCompare(String s, String t) {
int i = s.length()-1,j = t.length()-1;//Reverse traversal
int skipS = 0;//skip is used to record # the number
int skipT = 0;
while(i >= 0 || j >= 0){ //As long as there is a string that has not been traversed, it will be traversed all the time
//First find the first definite character in the s string in reverse order (reverse order)
while(i >= 0){
if(s.charAt(i) == '#'){ //The current character is#
skipS++; //#Quantity plus 1
i--;//Length - 1
}else if(skipS > 0){ //Indicates that the current character needs to be backspace
skipS--; //Back off once and reduce one#
i--; //Character backspace, length - 1
}else break; //If it is not equal to # and does not need to be whitespace, it means that the first character in the s string has been found and the loop can be exited
//Now let's find the first definite character in the T string (in reverse order)
}
while(j >= 0){
if(t.charAt(j) == '#'){
skipT++;
j--;
}else if(skipT > 0){
skipT--;
j--;
}else break;
}
//After the above processing, the first character is found in both strings. Now let's judge whether the two strings are equal
//Why judge whether j and i are greater than or equal to 0?
//Because if index = 0 is' # ', I and J will be - 1. Why?
//Because our judgment conditions are as follows:
//if(skipS > 0){
// skipS--;
// i--;
//If index=0 is #, then i and j are - 1
// The case of index = -1 should be handled.
if (i >= 0 && j >= 0)
{
// If the characters to be compared are different, return false
if (s.charAt(i) != t.charAt(j))
return false;
}
// (I > = 0 & & J > = 0) is false
// 1. i < 0 && j >= 0
// 2. j < 0 && i >= 0
// 3. i < 0 && j < 0
// Among them, the third case is consistent with the meaning of the question, because in this case, s and t are both index = 0, and the position is' # '
// A backspace blank character is a blank character, which also conforms to the meaning of the question and should return True.
// However, cases 1 and 2 do not conform to the meaning of the question, because one of s and t finds the character to be compared at index > = 0, and the other does not
// This situation is obviously not in line with the meaning of the question. You should return False. The following formula will deal with this situation.
else if (i >= 0 || j >= 0)
return false;
i--; //If the above operation is completed and the program is not exited, it means that the first match is equal, and the following loop can be executed
j--;
}
//Exit the loop without ending the program. The description is true
return true;
}
}
977. Square of ordered array

Idea:
This problem is best done with violence. It's just two steps. Take out each number to find the square value, and then load the result with a newly created array, sort and return the new array.
Other solutions will be analyzed later when redoing.
class Solution {
public int[] sortedSquares(int[] nums) {
int[] arr = new int[nums.length];
for(int i=0; i<nums.length ;i++){
arr[i] = nums[i] * nums[i];
}
Arrays.sort(arr);
return arr;
}
}
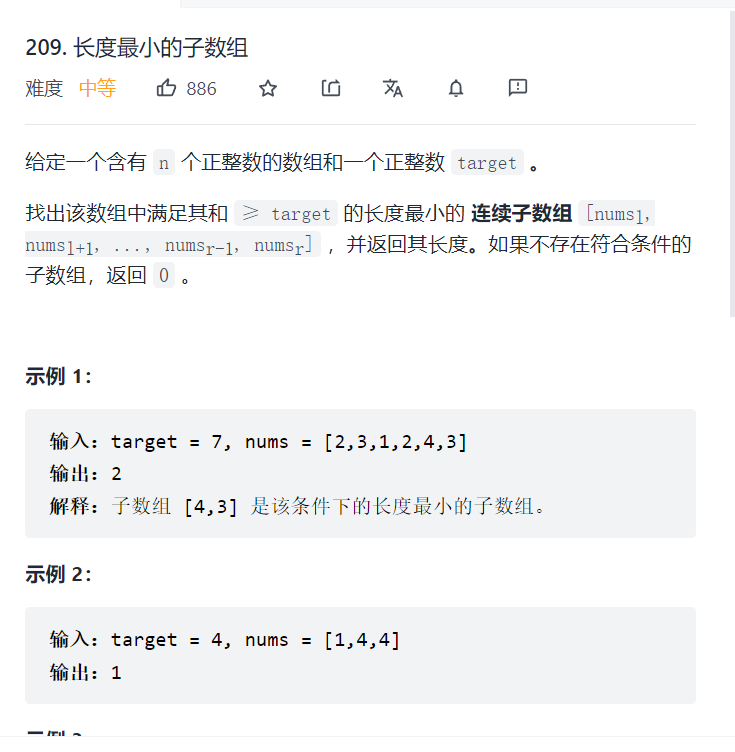
209. Minimum length subarray
Title Description:
Idea:
I directly use the violence search, the ideas are written in the code in great detail. A better way to think about it later.
class Solution {
public int minSubArrayLen(int s, int[] nums) {
int sum = 0; //Used to find the sum of continuous subarrays
int len = 0; //Used to find the length of the subarray
int res = Integer.MAX_VALUE;//Set the result value initially to infinity
//In this way, as long as an array length satisfying the > = target condition appears below
//Let's compare it with res
//If the length of the secondary subarray is smaller than res, we will refresh the value of res to the length of the secondary subarray
for(int i = 0; i < nums.length; i++){
sum = 0; //Sum. The sum value should be refreshed before each summation
for(int j = i; j < nums.length; j++){//Let j traverse backward from the current i index to find the subarray
sum = sum + nums[j];//Sum up the elements of the current subarray
if(sum >= s){ //This indicates that the currently traversed sub array is qualified
//Then we take out the length of this sub array
len = j - i + 1; //The index subtracts and adds 1, because the array counts from 0
//Compare the length of the current sub array with the size of the original res
if(len < res){ //If the length of the current subarray is less than the original res
//Refresh res value to smaller
res = len;
}
break; //Now that the qualified subarray has been found in the current sequence
//Then exit the loop after processing and continue the carpet search for the next qualified sub array
}
}
}
//Returns res if the value of res is still a predefined value
//If the description is not found, return 0
//If it is not the original value, we directly return res
return res == Integer.MAX_VALUE ? 0 : res;
}
}
One point is that because the infinity value is used in the problem solution, I also use the infinity value above, but in theory, as long as it is greater than or equal to the length range of the num array given by the problem. For example, 100000 does not have to use integer Maxvalue, I was confused at first.
904. Fruit baskets (difficult)

To tell you the truth, I haven't understood it yet. Write it down first and read it tomorrow.
// This question requires that you choose a subsequence with only two elements at most
class Solution {
public int totalFruit(int[] fruits) {
if(fruits.length == 1) {
return fruits.length;
}
int basket1 = -1, basket2 = -1; //Record the fruit in the current basket
int sum = 0;
int curFruit = -1, curFruitLoc = 0; //Record the current fruit and the starting position of the current fruit
int subSum = 0;
int j = 0; // Record basket start position
for (int i = 0; i < fruits.length; ++i) {
if (fruits[i] == basket1 || fruits[i] == basket2)
{
if (fruits[i] != curFruit) {// Record the continuous recent in the basket and use it when replacing the fruit in the basket
curFruit = fruits[i];
curFruitLoc = i;
}
}
else {
j = curFruitLoc;
curFruitLoc = i;
if (basket1 == curFruit) { // Renew fruit basket
basket2 = fruits[i];
curFruit = basket2;
}
else {
basket1 = fruits[i];
curFruit = basket1;
}
}
subSum = (i - j + 1); // Calculate the longest subsequence
sum = sum > subSum ? sum : subSum;
}
return sum;
}
}
59. Spiral matrix

Idea:
In the simulation process, the ideas are all in the code. If you don't understand, you can see the ideas in the code Capriccio. It can only be said that the ideas in some places are really exquisite.
class Solution {
public int[][] generateMatrix(int n) {
//Create a two-dimensional array that returns results
int[][] arr = new int[n][n];
int loop = n / 2; //Defining the number of cycles is actually defining the total number of turns of the spiral. If this is not taken into account, it is really difficult to write
//Define the starting position of each circle, because we rotate one circle at a time
int startX = 0;
int startY = 0;
//To assign a value to a two-dimensional array
int count = 1;
//Each loop controls the traversal length of each edge
int offset = 1;
//The mid value is used to determine whether this n is odd or even
//If it is an odd number, there will be one more position in the middle to form a circle separately (you can draw an even number to have a look)
//If it's an even number, it's OK. The middle can just form a loop
int mid = n / 2;
//Next, start the cycle processing (cycle by cycle)
while(loop > 0){ //Number of cycles
int i = startX;
int j = startY; //Both startX and startY need to be recorded in the whole process, so we need to use two temporary variables instead
//First perform a left to right traversal
for(;j < startY + n - offset;j++){//The judgment condition here is the finishing touch and you have to taste it well
arr[startX][j] = count;
count++;
}
//Then perform from top to bottom
for(;i < startX + n - offset;i++){//In fact, startX can be written as startY, because these two values are always the same
arr[i][j] = count;
count++;
}
//Then execute from right to left
for(;j > startY;j--){
arr[i][j] = count;
count++;
}
//The final execution is from bottom to top
for(;i > startX;i--){
arr[i][j] = count;
count++;
}
//After each turn, startX and startY should move to the inner circle for the next turn
startX++;
startY++;
//One turn will reduce the total number of turns
loop--;
//Turn around and the side length offset will also change
//For each turn, the next turn will be reduced by 2, that is, the offset will be reduced by 2
//We write + 2 because the offset in the above loop is the subtracted number
offset = offset + 2;
}
//When you exit the loop, the traversal has ended
//One more thing to judge here is
//If the parity of n is even, there is no problem, and the above can be traversed
//However, if it is an odd number, there will be another position left in the middle
if(n % 2 != 0){
arr[mid][mid] = count;//count has reached the last value after processing in the loop
}
return arr;
}
}
54. Spiral matrix

The ideas are in the code. This spiral matrix problem is just to treat the matrix as a circle layer by layer
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
//Return result set
List<Integer> list = new ArrayList<>();
int hang = matrix.length;//Gets the number of rows of a two-dimensional array
int lie = matrix[0].length; //Gets the number of columns of a two-dimensional array
//Divide the rectangle into four corners and traverse the output layer by layer
int top = 0; //(top,left) upper left corner
int left = 0; //(top,right) upper right corner
int bottom = hang - 1; //Bottom, left
int right = lie - 1; //Bottom, right
//Traversal search
while(top <= bottom && left <= right){
//From left to right
for(int i=left;i <= right;i++){
list.add(matrix[top][i]);
}
//From top to bottom
for(int i=top+1;i <= bottom;i++){//top+1 is because you want to jump to the second line
list.add(matrix[i][right]);
}
if(left < right && top < bottom){//To exclude the case where left==right and top==bottom
//Because this situation will cause duplicate data records
//For example, if the input data is [[3], [2]], the output will be [3,2,2] if the equality is not excluded
//From right to left
for(int i=right-1;i > left;i--){
list.add(matrix[bottom][i]);
}
//Bottom up
for(int i=bottom;i > top;i--){
list.add(matrix[i][left]);
}
}
//After one circle at a time, the range is reduced by 1
top++;
left++;
bottom--;
right--;
}
return list;
}
}