Code Capriccio record brush problem introduction notes
Code Capriccio introduction
Code Capriccio record brush problem introduction notes
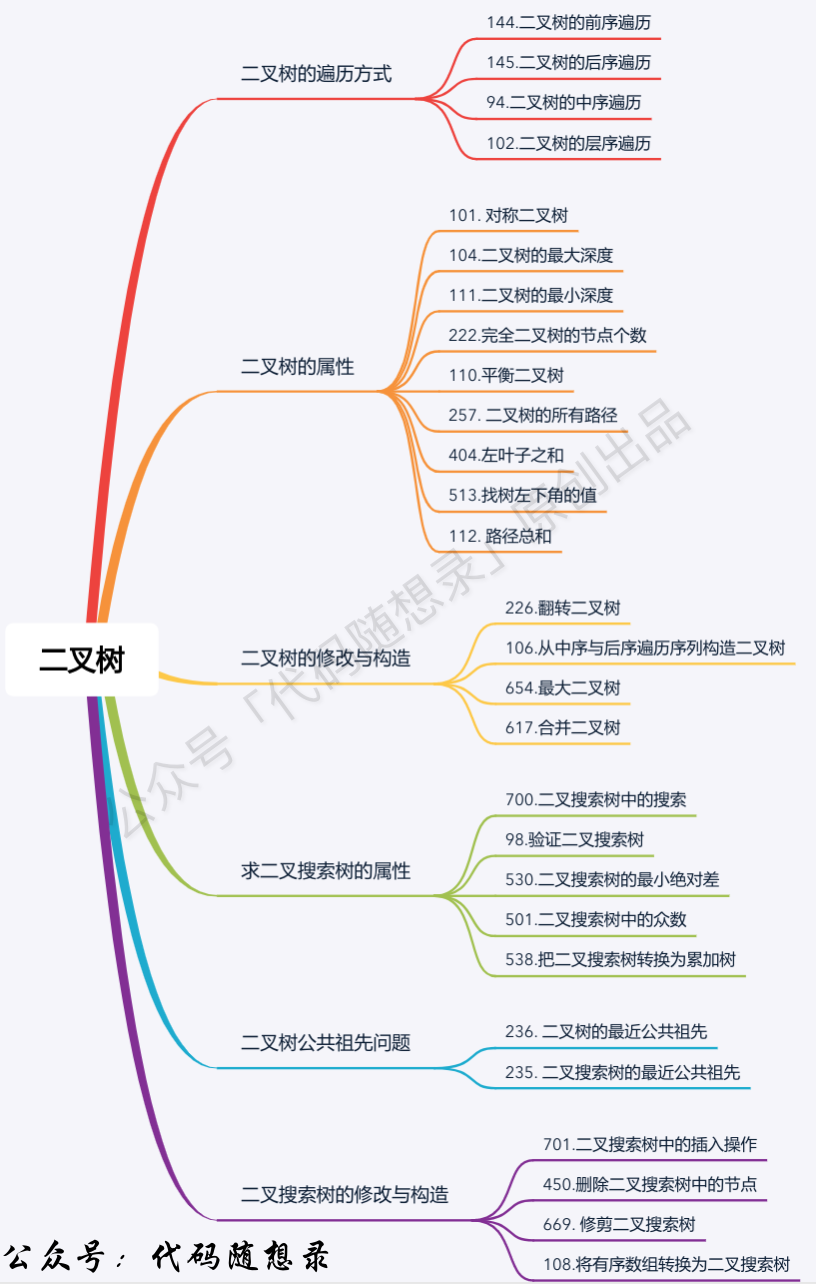
1. You should know this about binary tree!
Binary tree code
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
Test code
class Test{
public static void main(String[] args) {
TreeNode root = createTree("[2,1,3,null,4,null,7]");
Solution solution = new Solution();
}
// The input format of string is: "[2,1,3,null,4,null,7]"
public static TreeNode createTree(String string){
if (string.equals("[]")){
return null;
}
ArrayList<Integer> list = new ArrayList<>();
String temp = "";
for (int i = 1; i < string.length(); i++) {
char ch = string.charAt(i);
if (ch == ',' || ch == ']') {
if (temp.equals("null")) {
// The null point is first assigned to infinitesimal and then pruned
list.add(Integer.MIN_VALUE);
}else {
list.add(Integer.valueOf(temp));
}
temp = "";
}else {
temp += ch;
}
}
if (list.get(0) == Integer.MIN_VALUE){
return null;
}
TreeNode root = new TreeNode();
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
TreeNode cur;
for (int i = 0; i < list.size(); i++) {
cur = queue.poll();
cur.val = list.get(i);
// The null point is first assigned to infinitesimal and then pruned
cur.left = new TreeNode(Integer.MIN_VALUE);
cur.right = new TreeNode(Integer.MIN_VALUE);
queue.offer(cur.left);
queue.offer(cur.right);
}
// Prune and delete the child node whose value is infinitesimal
queue.clear();
queue.offer(root);
while (!queue.isEmpty()) {
cur = queue.poll();
if (cur.left.val == Integer.MIN_VALUE) {
cur.left = null;
}else {
queue.offer(cur.left);
}
if (cur.right.val == Integer.MIN_VALUE) {
cur.right = null;
}else {
queue.offer(cur.right);
}
}
return root;
}
}
2. Binary tree: as soon as you enter the recursion, it is as deep as the sea. From then on, the offer is a passer-by
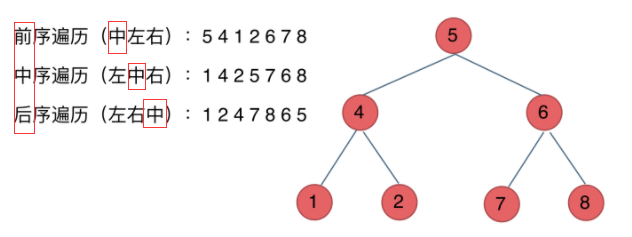
Binary tree traversal includes pre order, middle order, post order and level traversal. The difference between pre order, middle order and post order is that the relative order of the operations of the left and right nodes remains unchanged, and the operations of the middle node before, in and after the left and right nodes represent pre order, middle order and post order.
The algorithm da God Zuo Shen (Zuo Chengyun) took 100 days to build the foundation of algorithm and data structure to the advanced family bucket tutorial, and directly hit BTAJ and other front-line large manufacturers to ask the algorithm interview questions, real questions and detailed notes P6.5 Binary tree, basic lesson 5 topic 1: binary tree node structure, which explains the recursive and non recursive methods of first order, middle order and then order traversal.
The non recursive methods of the following three questions are in the next two chapters.
144. Preorder traversal of binary tree
Method 1: recursion
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
preOrderRecurrent(root, res);
return res;
}
public void preOrderRecurrent(TreeNode node, List<Integer> res){
if (node == null){
return;
}
res.add(node.val);
preOrderRecurrent(node.left, res);
preOrderRecurrent(node.right, res);
}
}
94. Middle order traversal of binary tree
Method 1: recursion
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
inOrderRecurrent(root, res);
return res;
}
public void inOrderRecurrent(TreeNode node, List<Integer> res){
if (node == null){
return;
}
inOrderRecurrent(node.left, res);
res.add(node.val);
inOrderRecurrent(node.right, res);
}
}
145. Post order traversal of binary tree
Method 1: recursion
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
postOrderRecurrent(root, res);
return res;
}
public void postOrderRecurrent(TreeNode node, List<Integer> res){
if (node == null){
return;
}
postOrderRecurrent(node.left, res);
postOrderRecurrent(node.right, res);
res.add(node.val);
}
}

3. Binary tree: it is said that what recursion can do, stack can also do!
Non recursive methods are divided into unified method and non unified method.
Unified method: the code structure of first order, middle order and later order is the same, and several codes are in different order;
Non unified method: the three code styles cannot be written in a unified way. Only the pre order and post order are similar, and the logic of the middle order is different from the other two.
The uniform law is introduced in the next chapter.
144. Preorder traversal of binary tree
Method 2: non recursive (stack) non unified method
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null){
return res;
}
Stack<TreeNode> stack = new Stack<>();
stack.add(root);
while (!stack.empty()){
TreeNode temp = stack.pop();
res.add(temp.val);
if (temp.right != null){
stack.push(temp.right);
}
if (temp.left != null){
stack.push(temp.left);
}
}
return res;
}
}
94. Middle order traversal of binary tree
Method 2: non recursive (stack) non unified method
Original method
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null){
return res;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.empty()){
if (cur != null){
stack.push(cur);
cur = cur.left;
}else{
cur = stack.pop();
res.add(cur.val);
cur = cur.right;
}
}
return res;
}
}
The left node needs to traverse to the end before it starts to traverse the right node, and the right node repeats the operation of traversing its own left node.
If else can be changed to while
modify
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) {
return res;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
res.add(cur.val);
cur = cur.right;
}
return res;
}
}
145. Post order traversal of binary tree
Method 2: non recursive (stack) non unified method
Original method
This is a modification based on the preorder traversal, which changes the preorder into middle right left, and then reverses the order. It is not a real postorder traversal.
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null){
return res;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.empty()){
TreeNode temp = stack.pop();
res.add(temp.val);
if (temp.left != null){
// Put left node
stack.push(temp.left);
}
if (temp.right != null){
// Put right node
stack.push(temp.right);
}
}
Collections.reverse(res);
return res;
}
}
If you do not use the reverse operation, you can use one more stack to collect Vals, and then spit out the stack to res.
modify
Real post order traversal.
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null){
return res;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;// This pointer is used to add nodes
TreeNode temp = null;// This pointer is used to judge the top node of the stack
TreeNode pre = null;// This pointer is used to judge whether the right node of the current node has been traversed
while (cur != null || !stack.empty()){
while (cur != null){
stack.push(cur);
cur = cur.left;
}
temp = stack.peek();
// Check whether the right node of the current node has been traversed. null is traversed
if (temp.right == null || temp.right == pre){
// The right node has been traversed
pre =stack.pop();
res.add(pre.val);
cur = null;
}else {
//Not traversed
cur = temp.right;
}
}
return res;
}
}
4. Binary tree: can't we unify the writing of the first, middle and last order iteration?
The non recursive (stack) unification method is inefficient because it adds a large number of null marks as the marks of nodes. Although one mark is used as three, it is inefficient and has little significance in the interview.
The core idea of this method: take the preorder as an example, pop up the stack node, turn the stack node into three nodes, press the three nodes into the stack, the order is right, left and middle null, the pop-up order is left and right in null, and null is the mark of the middle node, which means that the left and right child nodes of the middle node have been traversed.
144. Preorder traversal of binary tree
Method 3: non recursive (stack) unified method
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null){
return res;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
TreeNode cur = root.left;
while (!stack.empty()){
TreeNode temp = stack.pop();
if (temp != null){
// Since the stack order of the first order is about the middle, the stack order is right, left and middle
if (temp.right != null){
// Put right node
stack.push(temp.right);
}
if (temp.left != null){
// Put left node
stack.push(temp.left);
}
// Put in the middle node and null, and null is used as the tag of the middle node
stack.push(temp);
stack.push(null);
}else {
temp = stack.pop();
res.add(temp.val);
}
}
return res;
}
}
94. Middle order traversal of binary tree
Method 3: non recursive (stack) unified method
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null){
return res;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
TreeNode cur = root.left;
while (!stack.empty()){
TreeNode temp = stack.pop();
if (temp != null){
// Since the stacking order of the middle order is left, middle and right, the stacking order is right, middle and left
if (temp.right != null){
// Put right node
stack.push(temp.right);
}
// Put in the middle node and null, and null is used as the tag of the middle node
stack.push(temp);
stack.push(null);
if (temp.left != null){
// Put left node
stack.push(temp.left);
}
}else {
temp = stack.pop();
res.add(temp.val);
}
}
return res;
}
}
145. Post order traversal of binary tree
Method 3: non recursive (stack) unified method
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null){
return res;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
TreeNode cur = root.left;
while (!stack.empty()){
TreeNode temp = stack.pop();
if (temp != null){
// Since the stack order of the post order is left and right, the stack order is middle, right and left
// Put in the middle node and null, and null is used as the tag of the middle node
stack.push(temp);
stack.push(null);
if (temp.right != null){
// Put right node
stack.push(temp.right);
}
if (temp.left != null){
// Put left node
stack.push(temp.left);
}
}else {
temp = stack.pop();
res.add(temp.val);
}
}
return res;
}
}
5. Binary tree: sequence traversal!
The essence of hierarchical traversal is sequential traversal. However, it is not the array of output results that is spliced together, which is the order of first-order traversal, because the array of each layer is not filled with the array of the next layer.
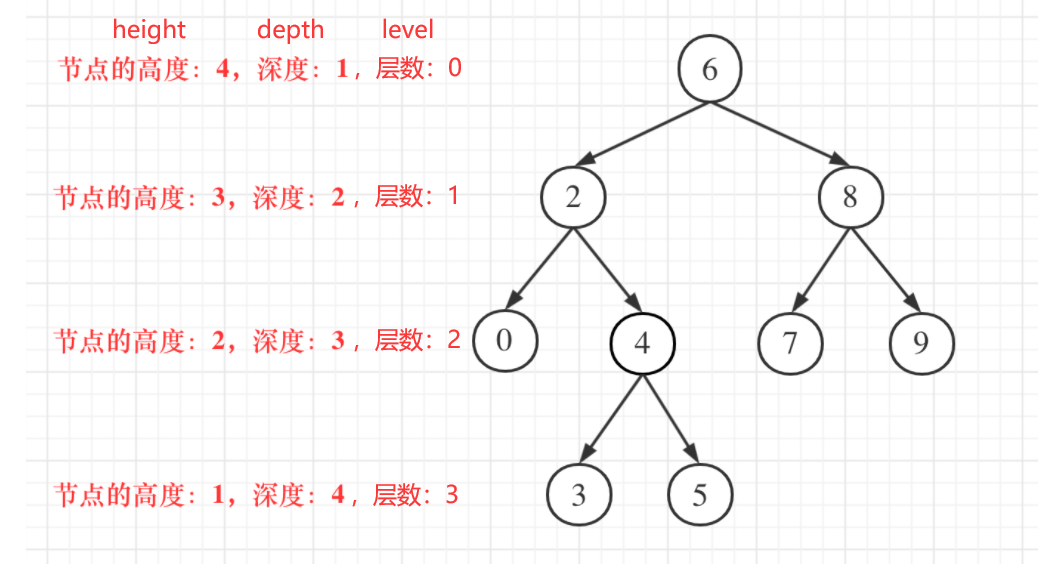
102. Sequence traversal of binary tree
Method 1: recursion
Use the number of layers as a variable
The root node represents layer 0. level represents the layer where the node is located.
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
ArrayList res = new ArrayList<>();
levelOrderRecurrent(root, 0, res);
return res;
}
public void levelOrderRecurrent(TreeNode node, int level, List<List<Integer>> res) {
if (node == null) {
return;
}
if (res.size() <= level) {
res.add(new ArrayList<>());
}
res.get(level).add(node.val);
levelOrderRecurrent(node.left, level + 1, res);
levelOrderRecurrent(node.right, level + 1, res);
return;
}
}
Use depth as a variable
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
ArrayList res = new ArrayList<>();
levelOrderRecurrent(root, 1, res);
return res;
}
public void levelOrderRecurrent(TreeNode node, int depth, List<List<Integer>> res) {
if (node == null) {
return;
}
if (res.size() < depth) {
res.add(new ArrayList<>());
}
res.get(depth - 1).add(node.val);
levelOrderRecurrent(node.left, depth + 1, res);
levelOrderRecurrent(node.right, depth + 1, res);
return;
}
}

Mode 2: non recursive (queue) non unified writing
Use a variable len to record the length of this layer, that is, the length of the current queue.
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
ArrayList res = new ArrayList<>();
if (root == null){
return res;
}
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
ArrayList<Integer> list = null;
TreeNode temp = null;
int len = 0;
while (!queue.isEmpty()){
len = queue.size();
list = new ArrayList<>();
while (len > 0){
temp = queue.pop();
list.add(temp.val);
if (temp.left != null){
queue.add(temp.left);
}
if (temp.right != null){
queue.add(temp.right);
}
len--;
}
res.add(list);
}
return res;
}
}
Mode 3: non recursive (queue) unified writing method
The tag that ends the layer with null.
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
ArrayList res = new ArrayList<>();
if (root == null){
return res;
}
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
queue.add(null);
ArrayList<Integer> list = new ArrayList<>();
TreeNode temp = null;
while (!queue.isEmpty()){
temp = queue.pop();
if (temp != null){
list.add(temp.val);
if (temp.left != null){
queue.add(temp.left);
}
if (temp.right != null){
queue.add(temp.right);
}
if (queue.peek() == null){
queue.add(null);
}
}else {
if (queue.isEmpty()){
break;
}
res.add(list);
list = new ArrayList<Integer>();
}
}
return res;
}
}
Supplementary topics
107. Hierarchical traversal of binary tree II
199. Right view of binary tree
637. Layer average of binary tree
Sequence traversal of 429.N-ary tree
515. Find the maximum value in each tree row
116. Fill in the next right node pointer of each node
117. Fill in the next right node pointer II of each node
104. Maximum depth of binary tree
111. Minimum depth of binary tree
6. Binary tree: can you really flip a binary tree?
226. Flip binary tree
First order and then order traversal can be done, and there are three methods respectively. There are no more than first exchange or first traversal, but the middle order can't be done, and there can't be interspersed exchange in traversal.
The following is a preliminary approach.
Method 1: recursion
class Solution {
public TreeNode invertTree(TreeNode root) {
preOrderRecurrentFun(root);
return root;
}
public void preOrderRecurrentFun(TreeNode node){
if (node == null){
return;
}
TreeNode temp = node.left;
node.left = node.right;
node.right = temp;
preOrderRecurrentFun(node.left);
preOrderRecurrentFun(node.right);
}
}
Method 2: non recursive (stack) non unified method
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null){
return root;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
TreeNode cur = null;
TreeNode temp = null;
while (!stack.empty()){
cur = stack.pop();
temp = cur.left;
cur.left = cur.right;
cur.right = temp;
if (cur.right != null){
stack.push(cur.right);
}
if (cur.left != null){
stack.push(cur.left);
}
}
return root;
}
}
7. Summary of this week! (binary tree)
8. Binary tree: am I symmetrical?
101. Symmetric binary tree
It's kind of like a preorder traversal. There are three ways.
Method 1: recursion
class Solution {
public boolean isSymmetric(TreeNode root) {
return compare(root.left, root.right);
}
private boolean compare(TreeNode left, TreeNode right) {
if (left == null && right != null) {
return false;
}
if (left != null && right == null) {
return false;
}
if (left == null && right == null) {
return true;
}
if (left.val != right.val) {
return false;
}
// Compare lateral
boolean compareOutside = compare(left.left, right.right);
// Compare inside
boolean compareInside = compare(left.right, right.left);
return compareOutside && compareInside;
}
}
Mode 2: non recursive (one-way queue)
class Solution {
public boolean isSymmetric(TreeNode root) {
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root.left);
queue.add(root.right);
TreeNode left = null;
TreeNode right = null;
while (!queue.isEmpty()){
left = queue.pop();
right = queue.pop();
if (left == null && right == null){
continue;
}
if (left == null || right == null || right.val != left.val){
return false;
}
queue.add(left.left);
queue.add(right.right);
queue.add(left.right);
queue.add(right.left);
}
return true;
}
}
Supplementary topics
100. Same tree
572. Subtree of another tree
9. Binary tree: look at the maximum depth of these trees
104. Maximum depth of binary tree
Method 1: recursion
Use the number of layers as a variable
The root node is layer 0, and its child node is layer 1, and so on. level represents the current layer and maxLevel represents the largest layer encountered. Tree structure with sequential records:

class Solution {
public int maxDepth(TreeNode root) {
return preOrderRecurrentFun(root, 0, -1) + 1;
}
public int preOrderRecurrentFun(TreeNode node, int level, int maxLevel){
if (node == null){
return maxLevel;
}
maxLevel = Integer.max(level, maxLevel);
int leftMaxLevel = preOrderRecurrentFun(node.left, level + 1, maxLevel);
int rightMaxLevel = preOrderRecurrentFun(node.right, level + 1, maxLevel);
maxLevel =Integer.max(leftMaxLevel, rightMaxLevel);
return maxLevel;
}
}
Use height as variable
There is also a tree structure of reverse order records, which records the maximum height of the current node subtree:

class Solution {
public int maxDepth(TreeNode root) {
return preOrderRecurrentFun(root);
}
public int preOrderRecurrentFun(TreeNode node){
if (node == null){
return 0;
}
int leftHeight = preOrderRecurrentFun(node.left);
int rightHeight = preOrderRecurrentFun(node.right);
return Integer.max(leftHeight, rightHeight) + 1;
}
}
Mode 2: non recursive
level traversal
class Solution {
public int maxDepth(TreeNode root) {
if (root == null){
return 0;
}
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
TreeNode temp = null;
int depth = 0;
int len = 0;
while (!queue.isEmpty()){
len = queue.size();
while (len > 0){
temp = queue.poll();
if (temp.left != null){
queue.offer(temp.left);
}
if (temp.right != null){
queue.offer(temp.right);
}
len--;
}
depth++;
}
return depth;
}
}
Supplementary topics
559.n maximum depth of fork tree
10. Binary tree: look at the minimum depth of these trees
111. Minimum depth of binary tree
Method 1: recursion
Post order traversal.
class Solution {
public int minDepth(TreeNode root) {
return postOrderRecurrentFun(root);
}
public int postOrderRecurrentFun(TreeNode node){
if (node == null){
return 0;
}
int leftMinDepth = postOrderRecurrentFun(node.left);
int rightMinDepth = postOrderRecurrentFun(node.right);
if (leftMinDepth == 0){
return rightMinDepth + 1;
}
if(rightMinDepth == 0){
return leftMinDepth + 1;
}
return Integer.min(leftMinDepth, rightMinDepth) + 1;
}
}
Mode 2: non recursive
class Solution {
public int minDepth(TreeNode root) {
if (root == null){
return 0;
}
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int depth = 0;
TreeNode temp = null;
int len = 0;
while (!queue.isEmpty()){
len = queue.size();
depth++;
while (len > 0){
temp = queue.poll();
// Leaf node return
if (temp.left == null && temp.right == null){
return depth;
}
if (temp.left != null){
queue.offer(temp.left);
}
if (temp.right != null){
queue.offer(temp.right);
}
len--;
}
}
return depth;
}
}
11. Binary tree: how many nodes do I have?
222. Number of nodes of complete binary tree
Method 1: recursion
class Solution {
public int countNodes(TreeNode root) {
return recurrentFun(root);
}
public int recurrentFun(TreeNode node){
if (node == null){
return 0;
}
return recurrentFun(node.left) + recurrentFun(node.right) + 1;
}
}
Mode 2: non recursive
Hierarchical traversal.
class Solution {
public int countNodes(TreeNode root) {
if (root == null){
return 0;
}
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int res = 0;
TreeNode temp = null;
int len = 0;
while (!queue.isEmpty()){
len = queue.size();
while (len > 0){
temp = queue.poll();
res++;
if (temp.left != null){
queue.offer(temp.left);
}
if (temp.right != null){
queue.offer(temp.right);
}
len--;
}
}
return res;
}
}
12. Binary tree: am I balanced?
110. Balanced binary tree
Method 1: recursion
Use auxiliary class Result
Post order traversal.
class Solution {
public boolean isBalanced(TreeNode root) {
return recurrent(root).isBalanced;
}
public Result recurrent(TreeNode node){
Result res = new Result();
if (node == null){
return res;
}
Result leftRes = recurrent(node.left);
Result rightRes = recurrent(node.right);
res.height = Integer.max(leftRes.height, rightRes.height) + 1;
boolean isBalanced = true;
if (Math.abs(leftRes.height - rightRes.height) > 1){
isBalanced = false;
}
res.isBalanced = isBalanced && leftRes.isBalanced && rightRes.isBalanced;
return res;
}
}
class Result{
int height = 0;
boolean isBalanced = true;
public Result() {
}
public Result(int height, boolean isBalanced) {
this.height = height;
this.isBalanced = isBalanced;
}
}
Do not use auxiliary classes:
In fact, this is also a post order traversal, but it can be returned in advance. Just put this line of code
if (leftHeight == -1) {
return -1;
}
Moving down one line is actually post order traversal.
class Solution {
/**
* Recursive method
*/
public boolean isBalanced(TreeNode root) {
return getHeight(root) != -1;
}
private int getHeight(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = getHeight(root.left);
if (leftHeight == -1) {
return -1;
}
int rightHeight = getHeight(root.right);
if (rightHeight == -1) {
return -1;
}
// The height difference between the left and right subtrees is greater than 1. return -1 indicates that it is no longer a balanced tree
if (Math.abs(leftHeight - rightHeight) > 1) {
return -1;
}
return Math.max(leftHeight, rightHeight) + 1;
}
}
Method 2: non recursive
Because we want to compare the height of the left and right nodes, we use the real post order traversal.
Violent iterative method
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null){
return true;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;// This pointer is used to add nodes
TreeNode temp = null;// This pointer is used to judge the top node of the stack
TreeNode pre = null;// This pointer is used to judge whether the right node of the current node has been traversed
while (cur != null || !stack.empty()){
while (cur != null){
stack.push(cur);
cur = cur.left;
}
temp = stack.peek();
// Check whether the right node of the current node has been traversed. null is traversed
if (temp.right == null || temp.right == pre){
// The right node has been traversed
if (Math.abs(getHeight(temp.left) - getHeight(temp.right)) > 1){
return false;
}
pre =stack.pop();
cur = null;
}else {
//Not traversed
cur = temp.right;
}
}
return true;
}
public int getHeight(TreeNode root){
if (root == null){
return 0;
}
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int len;
int depth = 0;
TreeNode temp;
while (!queue.isEmpty()){
len = queue.size();
while (len > 0) {
temp = queue.poll();
if (temp.left != null){
queue.offer(temp.left);
}
if (temp.right != null) {
queue.offer(temp.right);
}
len--;
}
depth++;
}
return depth;
}
}
optimization
The getHeight method of violent iteration method is optimized by using treenode Val to save the height of the current node, but I think this will destroy the value of the tree itself.
13. Binary tree: find all my paths?
257. All paths of binary tree
Method 1: recursion
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
ArrayList<String> res = new ArrayList<>();
recurrent(root, "", res);
return res;
}
public void recurrent(TreeNode node, String path, List<String> res){
if (node == null){
return;
}
path = path + String.valueOf(node.val);
recurrent(node.left, path + "->" , res);
recurrent(node.right, path + "->" , res);
if (node.left == null && node.right == null){
res.add(path);
}
}
}

Mode 2: non recursive
Hierarchical traversal.
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
ArrayList<String> res = new ArrayList<>();
if (root == null){
res.add("");
return res;
}
LinkedList<TreeNode> queue = new LinkedList<>();
ArrayList<String> curPaths;
ArrayList<String> oldPaths = new ArrayList<>();
oldPaths.add("");
queue.offer(root);
int len;
TreeNode temp;
String path;
while (!queue.isEmpty()){
len = queue.size();
curPaths = new ArrayList<>();
for (int i = 0; i < len; i++) {
temp = queue.poll();
path = oldPaths.get(i)+ String.valueOf(temp.val);
if (temp.left == null && temp.right == null) {
res.add(path);
continue;
}
if (temp.left != null){
queue.offer(temp.left);
curPaths.add(path + "->");
}
if (temp.right != null){
queue.offer(temp.right);
curPaths.add(path + "->");
}
}
oldPaths = curPaths;
}
return res;
}
}

14. Summary of this week! Binary tree Series II
15. Binary tree: I think recursion is used, but backtracking is hidden
16. Binary tree: after doing so many questions, what is the sum of my left leaves?
404. Sum of left leaves
Method 1: recursion
It has nothing to do with the left order in the process of traversing the leaves.
Judgment condition: if the left child node of the current point a is not empty, and the left and right child nodes of the left child node are empty, then the left child node of a is the left leaf node.
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
return recurrent(root);
}
public int recurrent(TreeNode node){
// level is the upper layer of the node, the root node is layer 0, and the upper layer of the root node is layer - 1
if (node == null) {
return 0;
}
int res = 0;
if (node.left != null) {
if (node.left.left == null && node.left.right == null){
res += node.left.val;
}
}
res += recurrent(node.left);
res += recurrent(node.right);
return res;
}
}
Mode 2: non recursive
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if (root == null){
return 0;
}
int res = 0;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
TreeNode temp;
while (!stack.empty()) {
temp = stack.pop();
if (temp.right != null){
stack.push(temp.right);
}
if (temp.left != null){
stack.push(temp.left);
if (temp.left.left == null && temp.left.right == null) {
res += temp.left.val;
}
}
}
return res;
}
}

17. Binary tree: what is the value of my lower left corner?
513. Find the value in the lower left corner of the tree
Method 1: recursion
Hierarchical traversal.
class Solution {
public int findBottomLeftValue(TreeNode root) {
if (root == null){
return 0;
}
ArrayList<List<Integer>> res = new ArrayList<>();
levelOrderRecurrent(root, 1, res);
return res.get(res.size() - 1).get(0);
}
public void levelOrderRecurrent(TreeNode node, int depth, List<List<Integer>> res) {
if (node == null) {
return;
}
if (res.size() < depth) {
res.add(new ArrayList<Integer>());
}
res.get(depth - 1).add(node.val);
levelOrderRecurrent(node.left, depth + 1, res);
levelOrderRecurrent(node.right, depth + 1, res);
return;
}
}
Mode 2: non recursive
Hierarchical traversal.
class Solution {
public int findBottomLeftValue(TreeNode root) {
if (root == null){
return 0;
}
int res = 0;
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int len;
TreeNode temp;
while (!queue.isEmpty()) {
len = queue.size();
res = queue.peek().val;
while (len > 0){
temp = queue.poll();
if (temp.left != null){
queue.offer(temp.left);
}
if (temp.right != null) {
queue.offer(temp.right);
}
len--;
}
}
return res;
}
}

18. Binary tree: path sum
112. Path sum
Method 1: recursion
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null){
return false;
}
return preOrderRecurrent(root, 0, targetSum);
}
public boolean preOrderRecurrent(TreeNode node, int sum, int targetSum){
sum += node.val;
if (sum == targetSum && node.left == null && node.right == null) {
return true;
}
boolean b1 = false;
boolean b2 = false;
if (node.left != null){
b1 = preOrderRecurrent(node.left, sum, targetSum);
// The left child node has found the path, and the right node does not need to find it
if (b1 == true){
return true;
}
}
if (node.right != null){
b2 = preOrderRecurrent(node.right, sum, targetSum);
}
return b1 || b2;
}
}

Mode 2: non recursive
Hierarchical traversal.
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) {
return false;
}
LinkedList<TreeNode> queue = new LinkedList<>();
ArrayList<Integer> curSums;
ArrayList<Integer> oldSums = new ArrayList<>();
oldSums.add(0);
queue.offer(root);
int len;
int curSum;
TreeNode temp;
while (!queue.isEmpty()) {
len = queue.size();
curSums = new ArrayList<>();
for (int i = 0; i < len; i++) {
temp = queue.poll();
curSum = oldSums.get(i) + temp.val;
if (curSum == targetSum && temp.left == null && temp.right == null) {
return true;
}
// oldSum.get(i) < targetSum
if (temp.left != null) {
queue.offer(temp.left);
curSums.add(curSum);
}
if (temp.right != null) {
queue.offer(temp.right);
curSums.add(curSum);
}
}
oldSums = curSums;
}
return false;
}
}
113. Path sum II
1
20. Binary tree: construct the largest binary tree
106. Construct binary tree from middle order and post order traversal sequences
leetcode address
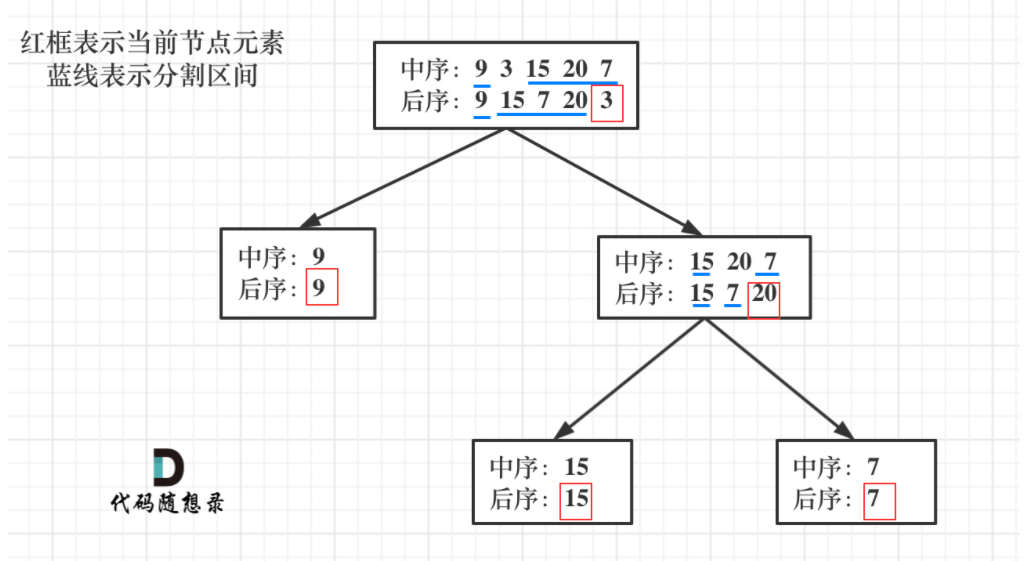
New left array:
New right array:
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
return Recurrent(inorder,0, inorder.length,
postorder, 0, postorder.length);
}
// Variables are closed on the left and open on the right. Left points to the starting position of the array and right points to the next position of the end element
public TreeNode Recurrent(int[] inorder, int inLeft, int inRight,
int[] postorder, int postLeft, int postRight){
if (inRight - inLeft == 0){
return null;
}
// 1. Find out the position of the node in the middle order array
int inMid = 0;
int postMid = postRight -1;// The position of the node in the subsequent array
for (int i = inLeft; i < inRight; i++) {
if (inorder[i] == postorder[postMid]){
inMid = i;
break;
}
}
TreeNode node = new TreeNode(postorder[postMid]);
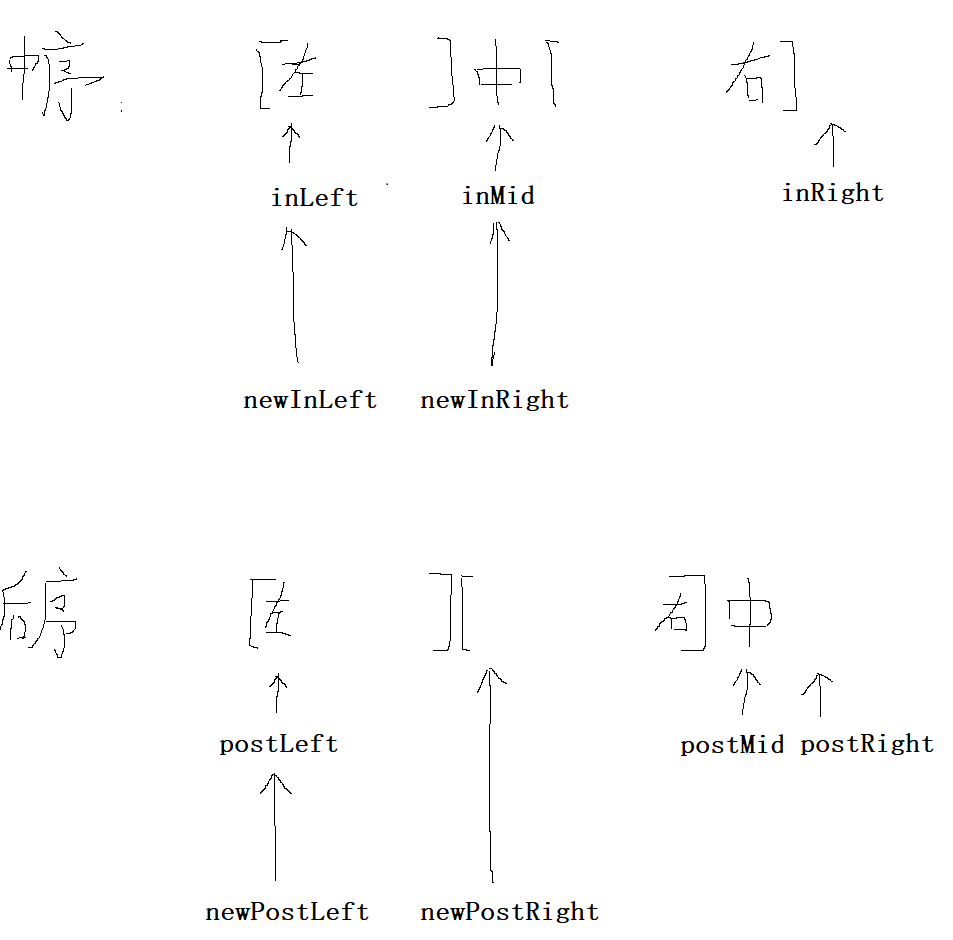
// 2. After partition, the left array information,
// If the pre ordered array has only one element, that is, inLeft + 1 = inRight,
// After partition, newInLeft == newInRight of the left array, that is, the left array has no elements.
// These variables are just easy to read. In practice, you can directly put the new value into the function
int newInLeft = inLeft;
int newInRight = inMid;
int newPostLeft = postLeft;
int newPostRight = postLeft + inMid - inLeft;
node.left = Recurrent(inorder, newInLeft, newInRight,
postorder, newPostLeft, newPostRight);
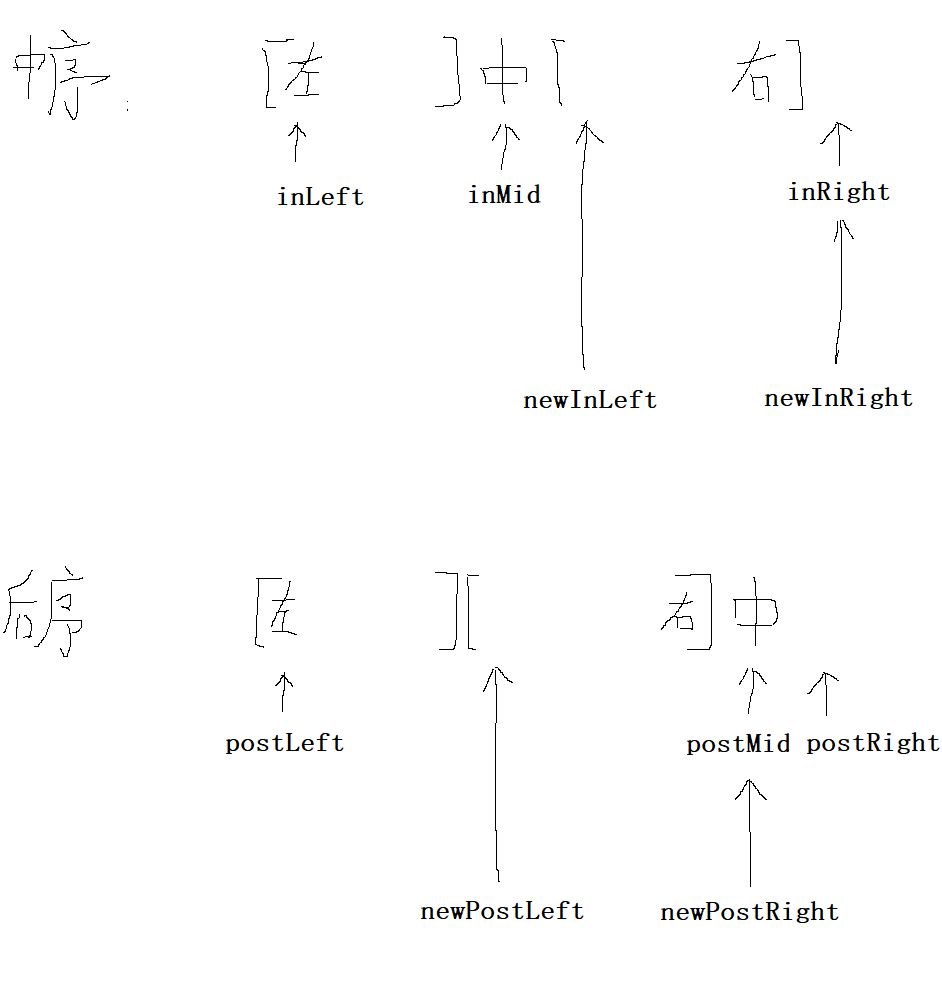
// 3. After division, right node information
newInLeft = inMid + 1;
newInRight = inRight;
newPostLeft = postLeft + inMid - inLeft;
newPostRight = postMid;
node.right = Recurrent(inorder, newInLeft, newInRight,
postorder, newPostLeft, newPostRight);
return node;
}
}
105. Construct binary tree from preorder and inorder traversal sequences
1
21. Summary of this week! (binary tree Series III)
22. Binary tree: merge two binary trees
617. Merge binary tree
It has nothing to do with the traversal of subsequent levels.
Method 1: recursion
New node
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
return recurrent(root1, root2);
}
public TreeNode recurrent(TreeNode node1, TreeNode node2){
if (node1 == null && node2 == null){
return null;
}
TreeNode node = new TreeNode();
if (node1 == null && node2 != null){
node.val = node2.val;
node.left = recurrent(null, node2.left);
node.right = recurrent(null, node2.right);
}
if (node1 != null && node2 == null) {
node.val = node1.val;
node.left = recurrent(null, node1.left);
node.right = recurrent(null, node1.right);
}
if (node1 != null && node2 != null) {
node.val = node1.val + node2.val;
node.left = recurrent(node1.left, node2.left);
node.right = recurrent(node1.right, node2.right);
}
return node;
}
}

New node only after merging
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
return recurrent(root1, root2);
}
public TreeNode recurrent(TreeNode node1, TreeNode node2) {
if (node1 == null) {
return node2;
}
if (node2 == null) {
return node1;
}
TreeNode node = new TreeNode(node1.val + node2.val);
node.left = recurrent(node1.left, node2.left);
node.right = recurrent(node1.right, node2.right);
return node;
}
}

Mode 2: non recursive
New node only after merging
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null){
return root2;
}
if (root2 == null) {
return root1;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode root = new TreeNode();
stack.push(root2);
stack.push(root1);
stack.push(root);
TreeNode node1;
TreeNode node2;
TreeNode cur;
while (!stack.empty()) {
cur = stack.pop();
node1 = stack.pop();
node2 = stack.pop();
cur.val = node1.val + node2.val;
// Process the right node of the current node
if (node1.right == null) {
cur.right = node2.right;
} else if (node2.right == null) {
cur.right = node1.right;
}else {
// node1.right != null && node1.right != null
stack.push(node2.right);
stack.push(node1.right);
cur.right = new TreeNode();
stack.push(cur.right);
}
// Process the left node of the current node
if (node1.left == null) {
cur.left = node2.left;
} else if (node2.left == null) {
cur.left = node1.left;
}else {
// node1.left != null && node1.left != null
stack.push(node2.left);
stack.push(node1.left);
cur.left = new TreeNode();
stack.push(cur.left);
}
}
return root;
}
}

23. Binary tree: binary search tree on stage!
700. Search in binary search tree
It has nothing to do with traversal.
Method 1: recursion
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
return preOrderRecurrent(root, val);
}
public TreeNode preOrderRecurrent(TreeNode node, int val) {
if (node == null) {
return null;
}
if (node.val == val) {
return node;
}
TreeNode left = preOrderRecurrent(node.left, val);
if (left != null) {
return left;
}
TreeNode right = preOrderRecurrent(node.right, val);
return right;
}
}

Mode 2: non recursive
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if (root == null){
return null;
}
Stack<TreeNode> stack = new Stack<>();
stack.add(root);
while (!stack.empty()){
TreeNode temp = stack.pop();
if (temp.val == val){
return temp;
}
if (temp.right != null){
stack.push(temp.right);
}
if (temp.left != null){
stack.push(temp.left);
}
}
return null;
}
}

24. Binary tree: am I a binary search tree
98. Verify binary search tree
If the nodes traversed in middle order are arranged in ascending order, then the tree is a binary search tree, which is the property of middle order. To compare in traversal, the most important thing is to record the value of the previous node.
Method 1: recursion
class Solution {
TreeNode min;
public boolean isValidBST(TreeNode root) {
return recurrent(root);
}
public boolean recurrent(TreeNode node) {
if (node == null) {
return true;
}
boolean leftRes = recurrent(node.left);
// If the left subtree is not satisfied, the lifting is terminated
if (!leftRes) {
return false;
}
if (min != null && min.val >= node.val) {
return false;
}
min = node;
boolean rightRes = recurrent(node.right);
return rightRes;
}
}
Mode 2: non recursive
class Solution {
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
TreeNode min = null;
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
if (min != null && min.val >= cur.val) {
return false;
}
min = cur;
cur = cur.right;
}
return true;
}
}

25. Binary tree: the minimum absolute difference of the search tree
530. Minimum absolute difference of binary search tree
Medium order traversal.
Method 1: recursion
class Solution {
TreeNode last;
int res = Integer.MAX_VALUE;
public int getMinimumDifference(TreeNode root) {
inOrderRecurrent(root);
return res;
}
public void inOrderRecurrent(TreeNode node){
if (node == null){
return;
}
inOrderRecurrent(node.left);
if (last != null){
res = Integer.min(res, Math.abs(last.val - node.val));
}
last = node;
inOrderRecurrent(node.right);
}
}
Mode 2: non recursive
class Solution {
public int getMinimumDifference(TreeNode root) {
if (root == null || (root.left == null && root.right == null)) {
return 0;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
TreeNode last = null; // Record previous node
int res = Integer.MAX_VALUE;
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
if (last != null) {
res = Integer.min(res, Math.abs(last. val - cur.val));
}
last = cur;
cur = cur.right;
}
return res;
}
}

26. Binary tree: what is my mode?
501. Mode in binary search tree
Medium order traversal.
Method 1: recursion
class Solution {
ArrayList<Integer> resList = new ArrayList<>();
int maxCount = 0;
int count = 0;
TreeNode pre = null;
public int[] findMode(TreeNode root) {
inOrderRecurrent(root);
int len = resList.size();
int[] res = new int[len];
for (int i = 0; i < len; i++) {
res[i] = resList.get(i);
}
return res;
}
public void inOrderRecurrent(TreeNode node) {
if (node == null) {
return;
}
inOrderRecurrent(node.left);
int rootValue = node.val;
// count
if (pre == null || rootValue != pre.val) {
count = 1;
} else {
count++;
}
// Update results and maxCount
if (count > maxCount) {
resList.clear();
resList.add(rootValue);
maxCount = count;
} else if (count == maxCount) {
resList.add(rootValue);
}
pre = node;
inOrderRecurrent(node.right);
}
}

Mode 2: non recursive
class Solution {
public int[] findMode(TreeNode root) {
ArrayList<Integer> resList = new ArrayList<>();
int maxCount = 0;
int count = 0;
TreeNode pre = null;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
if (cur != null) {
stack.push(cur);
cur = cur.left;
} else {
cur = stack.pop();
// count
if (pre == null || cur.val != pre.val) {
count = 1;
} else {
count++;
}
// Update results
if (count > maxCount) {
maxCount = count;
resList.clear();
resList.add(cur.val);
} else if (count == maxCount) {
resList.add(cur.val);
}
pre = cur;
cur = cur.right;
}
}
int len = resList.size();
int[] res = new int[len];
for (int i = 0; i < len; i++) {
res[i] = resList.get(i);
}
return res;
// return result.stream().mapToInt(Integer::intValue).toArray();
}
}

27. Binary tree: common ancestor problem
236. Nearest common ancestor of binary tree
Prerequisite: no duplicate nodes.
This problem belongs to backtracking. Non recursive method is not suitable for simulating the process of backtracking.
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return postOrderRecurrent(root, p, q);
}
public TreeNode postOrderRecurrent(TreeNode node, TreeNode p, TreeNode q) {
if (node == null || node == p || node == q) {// Recursive end condition
return node;
}
TreeNode left = postOrderRecurrent(node.left, p, q);
TreeNode right = postOrderRecurrent(node.right, p, q);
if (left == null && right == null) {// If node p or q is not found
return null;
}
if (left != null && right == null) {// If a node is found
return left;
}
if (left == null && right != null) {// If a node is found
return right;
}
// Both nodes found
return node;
}
}

28. Summary of this week! (binary tree Series IV)
29. Binary tree: the common ancestor of search tree
235. Nearest common ancestor of binary search tree
Precondition: the nodes are not duplicate, and the two input nodes of the node exist in the tree.
Independent of traversal order.
The relationship between nodes q and p is nothing more than the following three kinds: not including each other, q including p, p including q
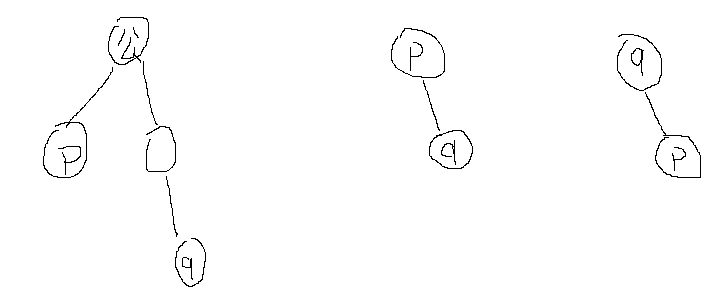
Then the common node s must be in the interval [p, q] or [Q, p].
When s is the left node of the parent node, it must be smaller than those on the right:
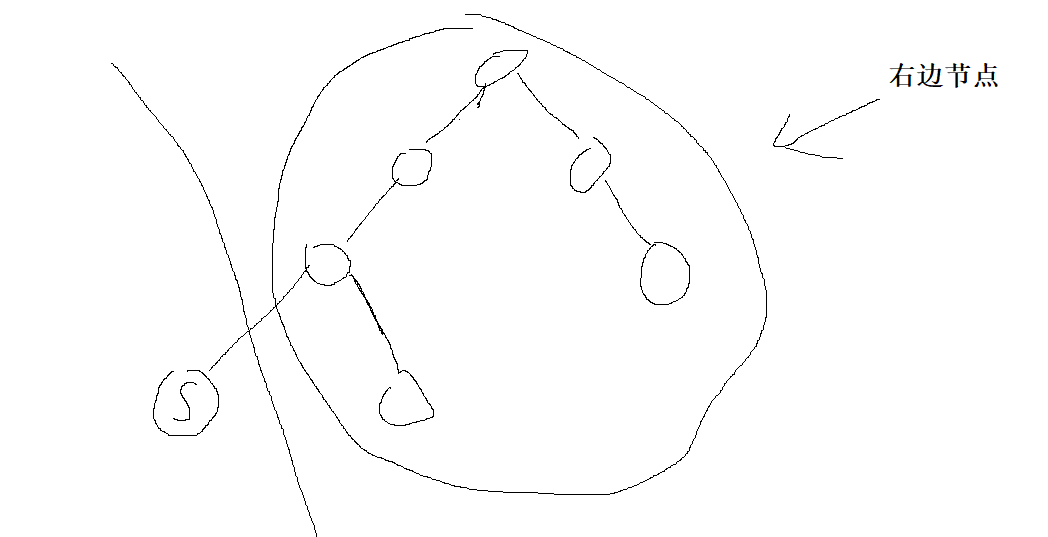
Similarly, when s is the right node of the parent node, it must be smaller than those on the left:
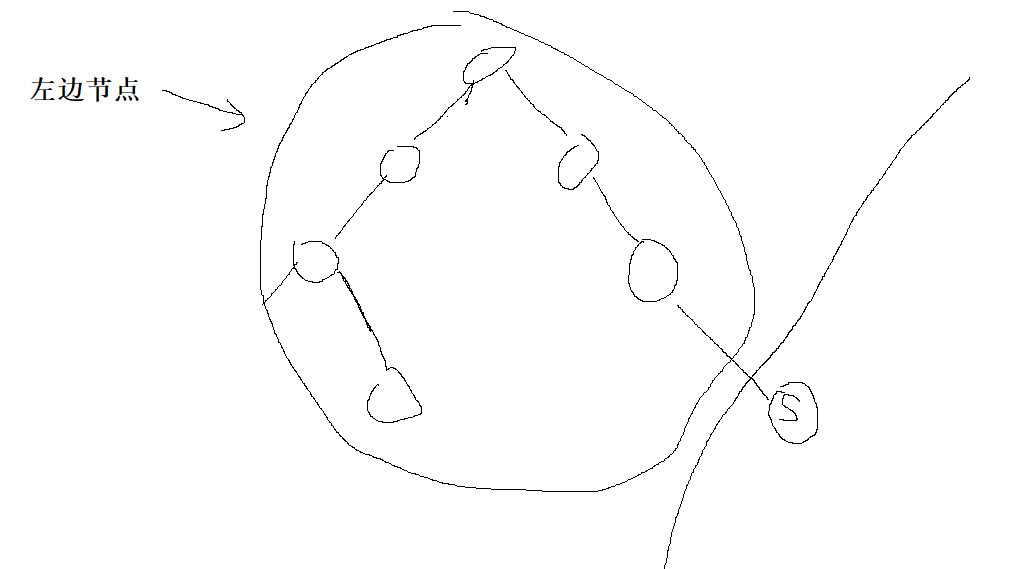
Method 1: recursion
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return recurrent(root, p, q);
}
public TreeNode recurrent(TreeNode node, TreeNode p, TreeNode q) {
if (node.val > p.val && node.val > q.val) {
return recurrent(node.left, p, q);
}
if (node.val < p.val && node.val < q.val) {
return recurrent(node.right, p, q);
}
return node;
}
}
Mode 2: non recursive
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
TreeNode temp = root;
while (true) {
if (temp.val > p.val && temp.val > q.val) {
temp = temp.left;
}else if (temp.val < p.val && temp.val < q.val) {
temp = temp.right;
}else {
return temp;
}
}
}
}
30. Binary tree: insert operation in search tree
701. Insert operation in binary search tree
Method 1: recursion
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
return recurrent(root,val);
}
public TreeNode recurrent(TreeNode node, int val){
if (node == null){
return new TreeNode(val);
}
if (node.val > val) {
node.left = recurrent(node.left, val);
}
if (node.val < val) {
node.right = recurrent(node.right,val);
}
return node;
}
}

Mode 2: non recursive
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) {
return root = new TreeNode(val);
}
TreeNode cur = root;
while (true) {
if (cur.val > val) {
if (cur.left == null) {
cur.left = new TreeNode(val);
return root;
}else {
cur = cur.left;
}
}else {
if (cur.right == null) {
cur.right = new TreeNode(val);
return root;
}else {
cur = cur.right;
}
}
}
}
}
31. Binary tree: delete in search tree
450. Delete nodes in binary search tree
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
return delete(root, key);
}
private TreeNode delete(TreeNode node, int key) {
if (node == null) {
return null;
}
if (node.val > key) {
node.left = delete(node.left, key);
} else if (node.val < key) {
node.right = delete(node.right, key);
} else {
// node.val == key, find
if (node.left == null) {
return node.right;
}
if (node.right == null) {
return node.left;
}
// Neither the left nor right child nodes are empty
TreeNode temp = node.right;
// Find the minimum value of the right subtree
while (temp.left != null) {
temp = temp.left;
}
// The minimum value is moved to the location where the node is deleted
node.val = temp.val;
// Delete the original minimum value
node.right = delete(node.right, temp.val);
}
return node;
}
}

Non recursive method is not suitable.
32. Binary tree: prune a search tree
669. Pruning binary search tree
Method 1: recursion
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
return recurrent(root, low, high);
}
public TreeNode recurrent(TreeNode node, int low, int high){
if (node == null) {
return null;
}
if (node.val > high) {
return recurrent(node.left, low, high);
}
if (node.val < low){
return recurrent(node.right, low, high);
}
node.left = recurrent(node.left, low, high);
node.right = recurrent(node.right, low, high);
return node;
}
}
Summary
The ideas of 30, 31 and 32 are very similar.
33. Binary tree: construct a search tree
108. Convert an ordered array into a binary search tree
Method 1: recursion
Left closed and right open [left, right], traversing in sequence first.
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return recurrent(nums, 0, nums.length);
}
public TreeNode recurrent(int[] nums, int left, int right) {
if (left >= right) {
return null;
}
if (right - left == 1) {
return new TreeNode(nums[left]);
}
int mid = left + ((right - left) >> 1);
TreeNode node = new TreeNode(nums[mid]);
node.left = recurrent(nums, left, mid);
node.right = recurrent(nums, mid + 1, right);
return node;
}
}

Mode 2: non recursive
Left closed and right open [left, right], traversing the hierarchy.
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
if (nums.length == 0) return null;
//Root node initialization
TreeNode root = new TreeNode();
Queue<TreeNode> nodeQueue = new LinkedList<>();
Queue<Integer> leftQueue = new LinkedList<>();
Queue<Integer> rightQueue = new LinkedList<>();
// Root node in queue
nodeQueue.offer(root);
// 0 is the initial position of the left interval subscript
leftQueue.offer(0);
// nums.size() is the initial position of the subscript in the right section
rightQueue.offer(nums.length);
while (!nodeQueue.isEmpty()) {
TreeNode cur = nodeQueue.poll();
int left = leftQueue.poll();
int right = rightQueue.poll();
int mid = left + ((right - left) >> 1);
// Give the element corresponding to mid to the intermediate node
cur.val = nums[mid];
// Processing left interval
if (left < mid) {
cur.left = new TreeNode();
nodeQueue.offer(cur.left);
leftQueue.offer(left);
rightQueue.offer(mid);
}
// Processing right interval
if (right > mid + 1) {
cur.right = new TreeNode();
nodeQueue.offer(cur.right);
leftQueue.offer(mid + 1);
rightQueue.offer(right);
}
}
return root;
}
}

Two more queues are used to simulate the input parameters in recursion.
34. Binary tree: convert the search tree into an accumulation tree
538. Convert binary search tree into cumulative tree
Middle order traversal of right, middle and left.
Method 1: recursion
class Solution {
int sum = 0;
public TreeNode convertBST(TreeNode root) {
recurrent(root);
return root;
}
public void recurrent(TreeNode node) {
if (node == null) {
return;
}
recurrent(node.right);
sum += node.val;
node.val = sum;
recurrent(node.left);
}
}
Mode 2: non recursive
class Solution {
public TreeNode convertBST(TreeNode root) {
int sum = 0;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
cur = cur.right;
}
cur = stack.pop();
sum += cur.val;
cur.val = sum;
cur = cur.left;
}
return root;
}
}

35. Binary tree: summary! (here are all the binary tree skills you need to master)
summary
if (Related to traversal) {
First order, middle order and then order level traversal;
Properties of various traversals:
For example, if the sequence traversed in middle order is arranged in descending order, it is a search binary tree
if (recursion) {
1. Select input parameters
2. Termination conditions
3. This round of recursive operation
4. Return value
}else {
non-recursive
}
}else {
Independent of traversal
}
if (top-down) {
For example, calculate the depth and number of layers, and the number of layers down a single path
}else {
Bottom up
For example, recursively return the height of the subtree upward
}
Judgment conditions of various structures:
For example, the condition of leaf node: the child nodes of a node exist, and the left and right child nodes of the child node are empty;
