Resources for all experiments Link: https://pan.baidu.com/s/1lukZRM3Rsd1la35EyyJcvg Extraction code: iv72
catalog
- Write in front
- Problem description
- Description of algorithm principle for solving problems
- Solving two lines of code similarity: LCS
- LCS state transition equation:
- LCS question: the answer to the youngest question
- LCS problem: pseudo code
- LCS problem: space optimization
- LCS problem: time optimization
- Solution of LIS problem:
- Foreshadowing: prove that seq sequence must increase in order
- Maintenance sequence seq method
- The feasibility of maintaining seq method is proved as follows:
- Time complexity analysis of LIS greedy method:
- LCS time test
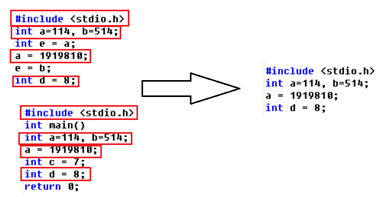
- Back to the duplicate check problem -- line code preprocessing:
- Algorithm test results
- Solutions for variable substitution:
- Improvement method 1: change the variables back
- Improvement method 2: null variable name
- Improved method 3: variable dependency mapping
- Results comparison
- A summary of the experience in solving this problem
- code
Write in front
At last, the algorithm class is coming to an end.
This semester's algorithm course is the most difficult course, and it happens to be an online course. There are relatively few opportunities for questioning and interaction. The teacher gives a lecture and the experiment content is relatively difficult. I spent most of my time looking for algorithms, implementing algorithms, and changing algorithm bug s.
I have also referred to many previous senior brother's reports, but most of them are abstract and obscure, and they only talk about methods without code, so it is difficult to understand the details of specific implementation.
So I'm going to record my report + code. The former coding the later copying. I hope that you can avoid detours...
Note: don't copy the code directly. It's Tower flushing! The shark is crazy and spicy.
Problem description
Question: according to the given repetition rate threshold r and template code file "A.cpp", calculate the maximum number of code repetition lines of test code file "B.cpp"?
1) A dynamic programming algorithm is designed to solve the problem of the longest identical sub code module of the file "A.cpp" in line i and the file "B.cpp" in line j, and a recursive formula is written to get the longest identical sub code module.
2) For any given i, j, find S(i,j). D(i,j) is calculated according to the given threshold r of repetition rate.
3) According to the calculated D(i,j), the maximum number of duplicate lines of test code file "B.cpp" is calculated by using dynamic programming algorithm? Write out the recurrence formula to get the most lines of repeated template code.
4) Design variable name replacement of different program code duplicate check (this problem is the plus point option).
Description of algorithm principle for solving problems
Solving two lines of code similarity: LCS
LCS is the longest common subsequence. It describes the common part between two sequences. The solution of LCs problem needs dynamic programming
LCS symbols and sub problem determination:
Suppose there are sequences s1 [] and s2 [], where s1 length is len1 and s2 length is len2, then the subproblem is to solve any subproblem of s1 s2 that is no longer than len1/len2 (there are multiple groups), which is the subproblem
How to describe LCS sub problem? :
s1[0~i] means to intercept the substring of subscript 0-i in s1
s2[0~j] means to intercept the substring of subscript 0-j in s2
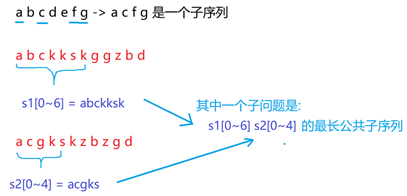
Solve the longest common subsequence of s1[0~i] and s2[0~j]. The solution of this subproblem is stored in dp[i][j]
LCS state transition equation:
Now we want to find the longest common subsequence length of s1[0i] and s2[0j] (the original problem), we naturally think that matching characters at s1[i] and s2[j] is no more than two cases: equal / unequal
We consider the case of equality: suppose we know that the longest common subsequence of s1[0~i-1] and s2[0~j-1] is gkd, as shown in the figure below. Because the current characters are equal, we can add the last bit to get the answer of the original question, that is, gkda
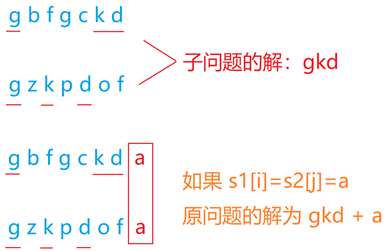
If s1[i] and s2[j] are not equal, but because a character is added, s1[0~i] and s2[0~j-1] or vice versa, s1[0~i-1] and s2[0~j] may extend the same subsequence

So we can launch: When s1[i] = s2[j], obviously dp[i][j] = dp[i-1][j-1]+1 When s1[i] ≠ s2[j], there are two possible answers: s1[0~i] and s2[0~j-1] perhaps The longest same subsequence length of s1[0~i-1] and s2[0~j] That is dp[i][j] = dp[i-1][j] or dp[i][j-1] Because we are looking for the longest identical subsequence, we take the maximum, that is, dp[i][j] = max(dp[i-1][j], dp[i][j-1])
LCS question: the answer to the youngest question
The LCS of the sequence with length 0 and any sequence is 0, that is dp[0][0] = dp[0][j] = dp[i][0] = 0
LCS problem: pseudo code
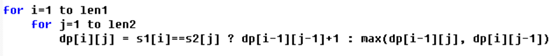
LCS problem: space optimization
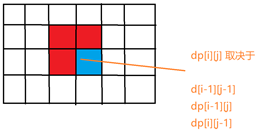
The spatial complexity of lcs problem is O(n^2) because of filling in the table, but because of the recursive structure of lcs problem, the answer of current problem only comes from the previous row and the answer of this row, we only need to save the answer of the previous row, that is, we can use the complexity of O(n) space to complete
LCS problem: time optimization
First, the LCS is transformed into LIS (longest ascending subsequence) problem
Because the essence of LCS problem is to select a certain subscript sequence in s1 and s2. The subscript sequence rises, that is, select the ascending subsequence, and then the characters corresponding to these ascending subsequences should be consistent
Then we count the subscripts of all the characters in s1 in s2, and sort each character x in descending order according to the subscript appearing in x (to prevent multiple choices of one word), and then splice them in the order in s1 to get the subscript sequence, and then calculate LIS for the subscript sequence. The length of LIS is the answer to the question

Solution of LIS problem:
Using dynamic programming to solve LIS problem, the time complexity is still O(n^2), but LIS can be solved by greedy method.
Solve LIS of nums [] array (i.e. subscript sequence mentioned above) by maintaining sequence seq []
seq[i] represents the minimum ending number of ascending subsequence with length i+1 in nums [] array
After the solution, the length of seq is the length of LIS (please keep this definition in mind, which will be used repeatedly later)
Foreshadowing: prove that seq sequence must increase in order
Using the counter proof method, if there is SEQ [i] > seq[j] and I < J, then we can find any ascending subsequence with length of j+1 and ending number of seq[j], column L, and cut the length of j-i from the end, so l becomes ascending subsequence with length of i+1

Because L is an ascending subsequence, all of which have L [i] < L [J] = seq [J] < seq[i], then we find an ascending subsequence with length i+1 and ending subscript smaller than seq[i], which contradicts the fact that seq [] keeps the smallest ending
Maintenance sequence seq method
- Traverse numbers in nums [] in order
- Find the first number seq[x] greater than or equal to nums[i] in seq
- If seq[x] is found, replace seq[x] with nums[i], if not, add nums[i] to the end of seq
The feasibility of maintaining seq method is proved as follows:
Because seq[x-1] must be less than nums[i], i.e. there is an ascending subsequence with length x, and its end is less than nums[i]
So add nums[i] after the ascending sequence of length x to get the ascending sequence of length x+1
And the end of this new sequence is nums[i], which is smaller than the original seq[x], so replace seq[x] with nums[i]
Time complexity analysis of LIS greedy method:
Because the sequence of seq is ordered, we can use binary search to find the first seq[x] larger than nums[i]. It needs O(n) to traverse nums [], and it needs O(log(n)) to binary search seq sequence every time, which keeps the time complexity of the algorithm at O(nlog(n))
LCS time test
Using random strings of different sizes to test, random numbers and letters
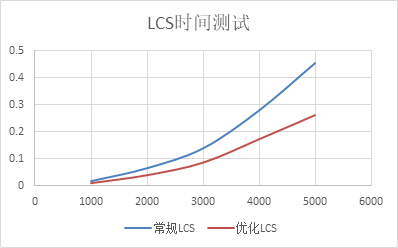
It can be seen that under different scales, the optimized LCS speed is much faster than that of conventional LCS, but because the character range of random characters is only 62 (letters + numbers + uppercase letters), the longer the test string is, the higher the frequency of the same characters is, and the easier it is to approach the worst case of optimized LCS (that is, s1=aaa s2=aaa Most afraid that a character appears many times in s2), so it is concluded that LCS time optimization is an unstable optimization
Its lower bound is O(nlong(n)), where n is the length of the short string in s1 s2, and its upper bound is O(n^2 * log(n^2)), but in the actual test, the overall optimization situation is acceptable
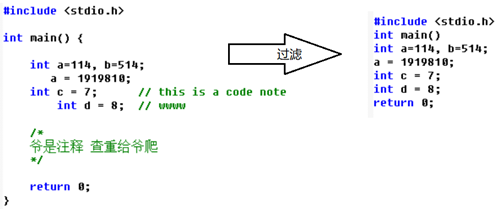
Back to duplicate query - line code preprocessing:
The read code can't directly calculate the LCS of lines. Because different people have different coding habits, the strategies of space, carriage return, empty line, TAB indent, bracket placement and comment habits are different, and the LCS results of lines will produce great errors, so it is necessary to filter and preprocess each line of code entered:
Remove leading and trailing spaces, blank lines, TAB indents, {} brackets, comments / / and/*
Line code LCS and duplicate check:
Back to the problem of LCs duplicate checking, now we have mastered the method of finding the similarity of two lines of code, that is, solving the LCS of two lines of code, and getting the similarity matrix D [] [], so how to analyze it?
Violent match for each line:
Enumerate each line of a.cpp and the repeated lines in b.cpp one by one to get the number of all repeated lines. Then, for each line of b.cpp, find the number of repeated lines in a.cpp, and then select the party with large proportion of repetition as the repetition rate
LCS by behavior unit:
If each line is regarded as an element, then a code is still a sequence. D[I][J] stores whether the lines are equal to each other. Therefore, we can find the LCS of lines and the length of similar line code sequence
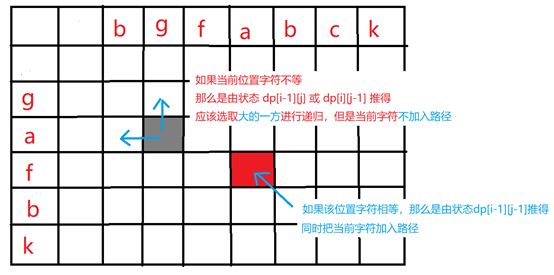
LCS path printing:
According to the two-dimensional array dp [] [] obtained by LCS, we can judge where the current state is derived from, and then find the recurrence path
If the characters in the current position are equal, it is derived from the state of i-1 j-1, so the current character is added to the path and recursion to i-1, j-1
If the characters in the current position are not equal, it means that i-1, j or i, j-1 deduces it. Select the large side to print the path recursively, but do not add the current character to the path
Algorithm test results
As shown in the figure, there are source codes of a.cpp and b.cpp. For b.cpp, some irrelevant codes are added to a.cpp to achieve the purpose of confusion

(here, LCS is used to solve the similarity of two lines of code, and then LCS or violence matching is used to solve the number of duplicate lines of code.)
Line LCS: as you can see, insert some irrelevant statements, and the obvious copied part can be detected by the LCS of the behavior unit
Violence: violence matching because the similarity of LCS is higher than the threshold, each line of a.cpp may have a higher matching degree with multiple lines of code in b.cpp, so there may be misjudgment, but most of the copied statements can be detected
Here, we use more code samples, additional tests, and the code samples are divided into four parts
- The non plagiarized code is two completely different codes
- Completely copied code is copied + a little change
- Sequential replacement code is the sequential replacement of parts of a code block
- Variable replacement is to replace the original variable name with a long and irregular string
(all subsequent tests are based on these four types of code test samples)

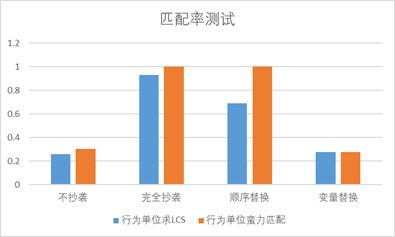
It can be seen that whether it is line LCS or line violence matching, in the case of complete plagiarism. All of them can be effectively checked out. In the data without plagiarism, we can achieve "no killing good people". In the data with sequential replacement, the line violence matching effect is better than the line LCS, because the line violence matching does not consider the order, neither of them can check out plagiarism in the case of variable replacement
Edit distance
To solve the problem of false judgment of editing violent matching: introduce editing distance (use editing distance to solve similarity between two lines of code)
As shown in the figure, because LCS only considers order, it will lead to misjudgment. A long code may contain a short code sequence, but it is essentially two unrelated codes
Edit distance: Introduction
A string s1 reduces the number of operations of replacing a character by a character by adding a character, and becomes the string s2. The minimum number of these operations is the editing distance between them
The minimum editing distance between horse and ros is 3. The process is as follows
Horse → horse (replace 'h' with 'r')
rorse → rose (delete 'r')
ros e → ros (delete 'e')
Edit distance: dynamic solver
The dynamic programming solution of edit distance is similar to LCS, which is recursive by comparing characters, but the recurrence formula is slightly different.
For s1[i]=s2[j], if the editing distance of two equal characters is 0, then the editing distance between them is dp[i][j] = dp[i-1][j-1] For s1[i] ≠ s2[j], we have three schemes to convert s1 to s2 1. Delete the last bit of s1, then the answer will be changed to find the edit distance between s1[0~i-1] and s2[0~j] 2. Replace the last bit of s1 with the last bit of s2, and the answer becomes to find the edit distance between s1[0~i-1] and s2[0~j-1] 3. Add one character to the last bit of s1 and the last character of s2. Then the last bits of s1 and s2 are equal now. The answer is changed to find the edit distance between s1[0~i] and s2[0~j-1] Recursive: min(dp[i-1][j-1],dp[i-1][j], dp[i][j-1]) + 1 (+ 1 is due to an operation)
state equation

dp[i][j] = dp[i-1][j-1] (s1[i] == s2[j]) dp[i][j] = min(dp[i-1][j-1],dp[i-1][j], dp[i][j-1]) + 1 (s1[i] ≠ s2[j])
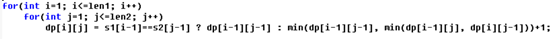
The time complexity is the same as that of LCS. In general, it is O(n^2). The time optimization algorithm of edit distance is not discussed here
Edit distance effect:
Use 1 – edit distance / max(len1, len2) to get the similarity (matching rate) between two lines of code, then match the lines of code, and output the matched lines of code

Through the above-mentioned matching rate and violent matching, it can be found that the matching effect is good, achieving 100% detection of plagiarized code lines, without being confused by other lines, because the editing distance not only considers the sequence between sequences, but also requires the length of the sequence. For two sequences with different length, the matching rate obtained by the editing distance will differ greatly from that obtained by LCS
Edit distance test (the similarity between two lines of code is solved by edit distance, and then LCS or violent matching is performed in behavioral units)
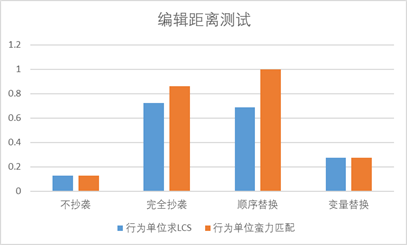
It can be seen that the effect of editing distance is similar to that of LCS in solving the similarity of two lines of code, because the essence of LCS is to find the similarity of two lines of code, and the essence of editing distance is to find the dissimilarity of two lines of code, and because there is no special example (i.e. "one line contains another line" misjudged code mentioned above), the effect is similar to that of LCS
Solutions for variable substitution:
As shown in the figure below, for the contents of a.cpp and b.cpp, all variable names are replaced, and the replaced variable names are quite long, which should be considered as complete plagiarism, but the similarity calculated by LCS or edit distance cannot be detected
The result of LCS / edit distance matching can only be matched to include, main and return 0. It needs to be improved
Improvement method 1: change the variables back
Replace the variables with abcdefg, and then match them
Improvement method 2: null variable name
Or you can choose to change the variable name to an empty string, only focus on the operation of the variable instead of the variable name, and then perform line LCS matching
Improved method 3: variable dependency mapping
There is a certain dependency between variables, for example, as shown in the figure, the value of a variable depends on the arr variable and b variable. Then, according to the left and right positions of variables in the assignment statement, we can get the dependency of variables and establish a digraph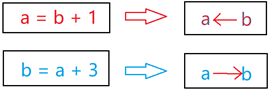
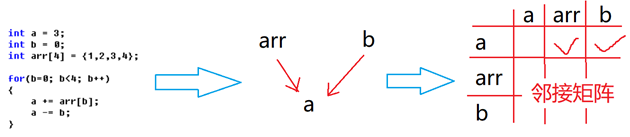
To build a digraph, we can recursively find out which variables affect the value of x
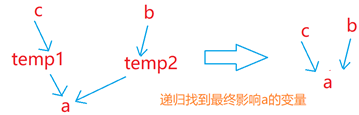
By comparing the "cosine similarity" between rows of the final adjacency matrix, it can be concluded that those statements are plagiarizing, while bypassing the influence of variable name (if the cosine similarity comparison exceeds the threshold, the row is plagiarism)
cosine similarity 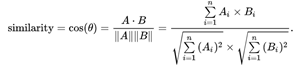
As shown in the figure below, the plagiarized lines can be found by matching the similarity of each row's adjacency matrix violently. Note that this method can not match all codes completely, only the variable assignment statement, namely the core code with constant variable dependency, can be matched

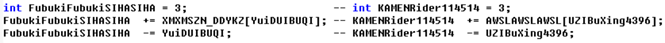
Results comparison
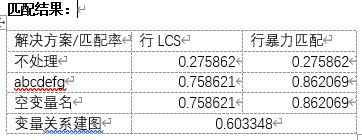
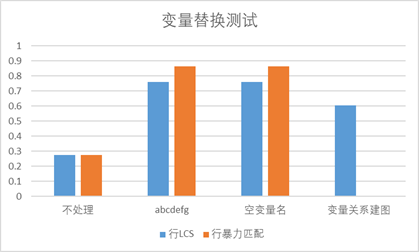
Conclusion: it can be seen that whether abcdefg or space is used to replace variable names, it has a good effect
The mapping of variable relationship is to match the key statements of variables, while other statements do not match, so the matching rate is low, but compared with the method of no processing, there is still a big improvement, so it is applicable to the detection of key statements in the secondary manual screening
A summary of the experience in solving this problem
Mastering the structure, use and common functions of string class in STL can greatly speed up the programming speed, especially the program involving a large number of string processing
The meaning of symbols and the definition of subproblems must be made clear before deriving dynamic programming equations
code
ps: there are others, but they are not realized or explained here
- Hungarian algorithm for maximum matching for maximum number of duplicate rows
- k-gram algorithm for row similarity
- A token based syntax automata for variable substitution

#include <bits/stdc++.h> using namespace std; /* * @function char_trim : Single line leading and leading filters filter leading and trailing spaces tab {} / / comments * @param s : String to filter * @return : Filtered string */ string char_trim(string &s) { int i=s.find("//"); if(i!=string::npos) s.erase(s.begin()+i, s.end()); while(s.back()=='}' || s.back()=='{' || s.back()==' ' || s.back()=='\t') s.pop_back(); while(s.length()>0 && s[0]==' ') s.erase(0, 1); while(s.length()>0 && s[0]=='\t') s.erase(0, 1); while(s.length()>0 && s[0]==' ') s.erase(0, 1); return s; } /* * @function line_trim : Remove the blank line tab {} / * / / comment from the general line filter of batch code * @param a : Code string array a[i] represents the code of the ith sentence * @return : ---- */ void line_trim(vector<string>& a) { for(int i=0; i<a.size(); i++) char_trim(a[i]); int flag=1, id; vector<string> b; for(int i=0; i<a.size(); i++) { id = a[i].find("/*"); // If the / * sign is not encountered, it will be regarded as a valid code if(id==string::npos) { if(flag==1) b.push_back(a[i]); } // Read to / * Ignore the line at first, but read it in / * Previous content else { string temp = a[i].substr(0, id); temp = char_trim(temp); b.push_back(temp); flag = 0; } id = a[i].find("*/"); // Read to * / end ignore read after * / at the same time if(id!=string::npos) { string temp = a[i].substr(id+2); temp = char_trim(temp); b.push_back(temp); flag = 1; } } a = b; for(int i=0; i<a.size(); i++) if(a[i].length()==0) a.erase(a.begin()+i), i--; } void print(vector<string>& a) { for(int i=0; i<a.size(); i++) cout<<a[i]<<endl; } /* * @function readfile : Read file as line string into lines * @param filepath : File path * @param lines : String array of received file lines * @return : ---- */ void readfile(string filepath, vector<string>& lines) { ifstream ifs(filepath); // Open file stream streambuf *ori_in = cin.rdbuf(); //Save the original I / O mode cin.rdbuf(ifs.rdbuf()); // Stream redirection while(getline(cin,filepath)) lines.push_back(filepath); // Read file lines ifs.close(); // Close flow cin.rdbuf(ori_in); //Back to console standard I / O } /* * @function writefile : Write string in lines array as line to file * @param filepath : File path * @param lines : Write content string array * @return : ---- */ void writefile(string filepath, vector<string>& lines) { ofstream ofs(filepath); // Open file stream streambuf *ori_out = cout.rdbuf(); //Save the original I / O mode cout.rdbuf(ofs.rdbuf()); // Stream redirection for(int i=0; i<lines.size(); i++) cout<<lines[i]<<endl; // Read file lines ofs.close(); // Close flow cout.rdbuf(ori_out); //Back to console standard I / O } /* * @function split_by : Split string array with given characters * @param s : Entire string to split * @param a : Array stored in each divided token * @param ch : Split by character ch * @return : ---- */ void split_by(string s, vector<string>& a, char ch) { int idx = s.find(ch); if(idx == string::npos) {a.push_back(s); return;} a.push_back(s.substr(0, idx)); split_by(s.substr(idx+1), a, ch); } /* * @function pure_var : Filter string by variable name rule, remove prefix, space, suffix and extract array name * @param a : Array of variable names * @return : ---- */ void pure_var(vector<string>& a) { for(int i=0; i<a.size(); i++) { a[i] = char_trim(a[i]); if('0'<=a[i][0] && a[i][0]<='9') {a.erase(a.begin()+i); i--; continue;} // The variable at the beginning of the number is not good int i1=a[i].find(' '), i2=a[i].find('='), i3=a[i].find(';'), i4=a[i].find('['); if(i1==string::npos) i1 = INT_MAX; if(i2==string::npos) i2 = INT_MAX; if(i3==string::npos) i3 = INT_MAX; if(i4==string::npos) i4 = INT_MAX; int id = min(min(i1, i2), min(i3, i4)); if(id < INT_MAX) a[i]=a[i].substr(0, id); } } /* * @function get_var : Get the variable name of the code string array * @param a : Code string array a[i] represents the code of the ith sentence * @return : String array holds variable name * @explain : Defect cannot detect custom data type */ static unordered_set<string> ha{"int", "float", "double", "long", "bool", "string"}; vector<string> get_var(vector<string>& a) { vector<string> vars; for(int i=0; i<a.size(); i++) { // If this line is in the application variable, i.e. none (), exclude the influence of functions such as int main() if(a[i].find('(')==string::npos && ha.find(a[i].substr(0, a[i].find_first_of(' ')))!=ha.end()) { string temp = a[i].substr(a[i].find_first_of(' ')+1); // Isolate variable types split_by(temp, vars, ','); // Separated by comma } } pure_var(vars); // Remove assignment = sign or semicolon or space after variable name return vars; } /* * @function replace_var : Replace variable name with abcdefg * @param a : Code string array a[i] represents the code of the ith sentence * @param vars : Variable name set * @return : ---- */ void replace_var(vector<string>& a, vector<string>& vars) { char var = 'a'; for(int i=0; i<vars.size(); i++) { for(int j=0; j<a.size(); j++) { while(1) { int idx = a[j].find(vars[i]); string newname = ""; newname += var; if(idx != string::npos) a[j].replace(idx, vars[i].length(), newname); else break; } } var++; } } /* * @function replace_var : Replace variable names with empty characters * @param a : Code string array a[i] represents the code of the ith sentence * @param vars : Variable name set * @return : ---- */ void replace_var_null(vector<string>& a, vector<string>& vars) { for(int i=0; i<vars.size(); i++) { for(int j=0; j<a.size(); j++) { while(1) { int idx = a[j].find(vars[i]); if(idx != string::npos) a[j].replace(idx, vars[i].length(), ""); else break; } } } } // end of declaration of util functions: end of character processing help function definition // -------------------------------------------------- // // Match algorithm definition in below /* * @function edit_dis : Find the editing distance between two strings, that is, s1. Add / replace / delete k characters can become s2 * @param s1 : String 1 * @param s2 : String 2 * @return : Edit distance between two strings */ int edit_dis(string s1, string s2) { int len1=s1.length(), len2=s2.length(); vector<vector<int>> dp(len1+1); for(int i=0; i<dp.size(); i++) dp[i].resize(len2+1); for(int i=1; i<=len1; i++) dp[i][0] = i; for(int i=1; i<=len2; i++) dp[0][i] = i; for(int i=1; i<=len1; i++) for(int j=1; j<=len2; j++) dp[i][j] = (s1[i-1]==s2[j-1])?(dp[i-1][j-1]):(min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1]))+1); return dp.back().back(); } /* * @function lcs : The longest similar subsequence -- space optimization solution * @param s1 : String 1 requiring solution * @param s2 : String 2 requiring solution * @return : Length of the longest identical subsequence * @explain : Complexity O(n^2) */ int lcs(string s1, string s2) { int len1=s1.length(), len2=s2.length(), last=0; vector<int> dp(len2+1); for(int i=1; i<=len1; i++) { last = 0; for(int j=1; j<=len2; j++) { int temp = dp[j]; dp[j] = (s1[i-1]==s2[j-1])?(last+1):(max(dp[j], dp[j-1])); last = temp; } } return dp.back(); } /* * @function lis : Solving the longest ascending subsequence -- time optimization * @param nums : Array of sequences to be solved * @return : Length of the longest ascending subsequence * @explain : Complexity O(nlog(n)) */ int lis(vector<int> nums) { if(nums.size()<2) return nums.size(); vector<int> seq{nums[0]}; for(int i=1; i<nums.size(); i++) { int j = lower_bound(seq.begin(), seq.end(), nums[i])-seq.begin(); if(j==seq.size()) seq.push_back(nums[i]); else seq[j]=nums[i]; } return seq.size(); } /* * @function lcs : Time optimal solution O(nlog(n)) * @param s1 : String 1 requiring solution * @param s2 : String 2 requiring solution * @return : Length of the longest identical subsequence * @explain : Complexity O(nlog(n)) */ int lcs1(string s1, string s2) { int len1=s1.length(), len2=s2.length(); unordered_map<char, vector<int>> hash; for(int i=len2-1; i>=0; i--) hash[s2[i]].push_back(i); vector<int> seq; for(int i=0; i<len1; i++) for(int j=0; j<hash[s1[i]].size(); j++) seq.push_back(hash[s1[i]][j]); return lis(seq); } /* * @function lcs_str_path : lcs path record for string array * @param dp : Dynamic planning lcs array needs to determine the direction according to it * @param D : String similarity list D[i][j] indicates whether line I of a.cpp and line j of b.cpp are similar * @param path : The array to store the path, path[0] corresponds to a.cpp_ Line, path[1] corresponds to b.cpp * @param i, j : Current position (row / column) of dp array lattice * @return : ---- */ void lcs_str_path(vector<vector<int>>& dp, vector<vector<int>>& D, vector<vector<int>>& path, int i, int j) { if(i<1 || j<1) return; if(D[i-1][j-1] == 1) { path.push_back(vector<int>{i-1, j-1}); lcs_str_path(dp, D, path, i-1, j-1); } else { if(dp[i][j]==dp[i][j-1]) lcs_str_path(dp, D, path, i, j-1); else lcs_str_path(dp, D, path, i-1, j); } } /* * @function lcs_str : Calculating lcs of string array * @param D : String similarity list D[i][j] indicates whether line I of a.cpp and line j of b.cpp are similar * @return : lcs Path array path an array of paths. path[0] corresponds to a.cpp_ Line, path[1] corresponds to b.cpp */ vector<vector<int>> lcs_str(vector<vector<int>>& D) { vector<vector<int>> mat(D.size()+1); for(int i=0; i<mat.size(); i++) mat[i].resize(D[0].size()+1); for(int i=1; i<mat.size(); i++) for(int j=1; j<mat[0].size(); j++) mat[i][j] = (D[i-1][j-1]==1)?(mat[i-1][j-1]+1):(max(mat[i-1][j],mat[i][j-1])); vector<vector<int>> ans; lcs_str_path(mat, D, ans, D.size(), D[0].size()); reverse(ans.begin(), ans.end()); return ans; } /* * @function lcs_str : Violence matches every line of code * @param D : String similarity S[i][j] indicates the similarity of a.cpp line I and b.cpp line j * @param r : Filter threshold * @return : The similar line path[0] in the two codes corresponds to a.cpp_ Line, path[1] corresponds to b.cpp */ vector<vector<int>> violate_match(vector<vector<int>>& S, double r) { vector<vector<int>> ans; for(int i=0; i<S.size(); i++) { int j = max_element(S[i].begin(), S[i].end()) - S[i].begin(); if(S[i][j] > r) ans.push_back(vector<int>{i, j}); } return ans; } /* * @function rate : LCS Calculate the repetition rate of two lines of code * @param s1 : String 1 * @param s2 : String 2 * @return : String similarity */ double rate_lcs(string s1, string s2) { return (double)lcs1(s1, s2) / (double)min(s1.length(), s2.length()); } /* * @function rate : Edit distance to calculate the repetition rate of two lines of code * @param s1 : String 1 * @param s2 : String 2 * @return : String similarity */ double rate_edis(string s1, string s2) { return 1.0 - (double)edit_dis(s1, s2) / (double)max(s1.length(), s2.length()); } vector<int> get_origin_var_adj(vector<vector<int>>& adj, int i) { vector<int> adji(adj[0].size()), temp; for(int j=0; j<adj[0].size(); j++) { if(adj[i][j]==1 && i!=j) { temp=get_origin_var_adj(adj,j); int cnt = 0; for(int k=0; k<temp.size(); k++) if(temp[k]==1) adji[k]=1; else cnt++; if(cnt == temp.size()) adji[j]=1; } } return adji; } /* * @function get_var_adj : Variable dependency mapping * @param lines : Each line of code * @param vars : Variable array * @return : Graph building of variable dependence -- adjacency matrix */ vector<vector<int>> get_var_adj(vector<string>& lines, vector<string>& vars) { vector<vector<int>> adj(vars.size()), adj_; for(int i=0; i<adj.size(); i++) adj[i].resize(vars.size()); for(int i=0; i<lines.size(); i++) { for(int j=0; j<vars.size(); j++) { // Find assignment statement vid is left eid equal sign int vid = lines[i].find(vars[j]); int eid = lines[i].find("="); // The statistical left value variables are related to those variables. Construct a graph (adjacency matrix) if(vid!=string::npos && eid!=string::npos && vid<eid) for(int k=0; k<vars.size(); k++) if(lines[i].find(vars[k])!=string::npos) adj[j][k]=1; } } for(int i=0; i<adj.size(); i++) // adj_.push_back(get_origin_var_adj(adj, i)); return adj; } /* * @function cos_sum : Computing cosine similarity of two vectors * @param v1 : Vector 1 * @param v2 : Vector 2 * @return : Vector similarity */ double cos_sim(vector<int> v1, vector<int> v2) { double su=0, sd=0, s1=0, s2=0; for(int i=0; i<v1.size(); i++) su+=(v1[i]*v2[i]); for(int i=0; i<v1.size(); i++) s1+=(v1[i]*v1[i]); s1=sqrt(s1); for(int i=0; i<v1.size(); i++) s2+=(v2[i]*v2[i]); s2=sqrt(s2); sd = s1 * s2; return su/sd; } int main() { /* // LCS Time optimization test int len=5000, batch=10, ans1, ans2; string chars = "1234567890abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ"; double t1=0, t2=0; clock_t st, ed; for(int t=0; t<batch; t++) { string s1, s2; for(int i=0; i<len; i++) s1 += chars[rand()%chars.length()]; for(int i=0; i<len; i++) s2 += chars[rand()%chars.length()]; // cout<<s1<<endl<<s2<<endl; st = clock(); ans1 = lcs(s1, s2); ed = clock(); t1 += (double)(ed-st)/CLOCKS_PER_SEC; st = clock(); ans2 = lcs1(s1, s2); ed = clock(); t2 += (double)(ed-st)/CLOCKS_PER_SEC; cout<<t<<endl; } cout<<t1/batch<<endl<<t2/batch<<endl; */ /* // Line code filter test vector<string> a; readfile("Filtration test. cpp", a); cout<<"Filter test. cpp original code: "< endl; print (a); cout < < endl; // Line filter code line_trim(a); cout<<"Filter test. cpp filtered Code: "< endl; print (a); cout < < endl; */ // Variable graph relationship building test /* vector<string> a; readfile("aaa.cpp", a); cout<<"aaa.cpp Original code: "< endl; print (a); cout < < endl; // Line filter code line_trim(a); cout<<"aaa.cpp Code after filtering: "< endl; print (a); cout < < endl; // Extract variables vector<string> a_vars = get_var(a); cout<<"aaa.cpp Variable extraction: "< endl; print (a)_ vars); cout<<endl; // replace_var_null(a, a_vars); // cout<<"a.cpp Code after replacing variable: "< endl; print (a); cout < < endl; // Extract variable graph relationship vector<vector<int>> adj = get_var_adj(a, a_vars); for(int i=0; i<adj.size(); i++) { for(int j=0; j<adj[0].size(); j++) { cout<<adj[i][j]<<" "; } cout<<endl; } */ // test vector<string> a, b; // read source file readfile("a4.cpp", a); cout<<"a.cpp Original code:"<<endl; print(a); cout<<endl; // Line filter code line_trim(a); cout<<"a.cpp Filtered code:"<<endl; print(a); cout<<endl; // Extract variables vector<string> a_vars = get_var(a); cout<<"a.cpp Variable extraction:"<<endl; print(a_vars); cout<<endl; replace_var_null(a, a_vars); // replace_var(a, a_vars); cout<<"a.cpp Code after replacing variable:"<<endl; print(a); cout<<endl; cout<<endl<<"--------------------------------"<<endl<<endl; // read source file readfile("b4.cpp", b); cout<<"b.cpp Original code:"<<endl; print(b); cout<<endl; // Line filter code line_trim(b); cout<<"b.cpp Filtered code:"<<endl; print(b); cout<<endl; // Extract variables vector<string> b_vars = get_var(b); cout<<"b.cpp Variable extraction:"<<endl; print(b_vars); cout<<endl; replace_var_null(b, b_vars); // replace_var(b, b_vars); cout<<"b.cpp Code after replacing variable:"<<endl; print(b); cout<<endl; cout<<endl<<"--------------------------------"<<endl<<endl; // Calculate the S / D matrix of matching rate #define r 0.9 vector<vector<int>> D(a.size()), S(a.size()); for(int i=0; i<S.size(); i++) S[i].resize(b.size()), D[i].resize(b.size()); for(int i=0; i<S.size(); i++) for(int j=0; j<S[0].size(); j++) S[i][j] = rate_lcs(a[i],b[j]), D[i][j]=(S[i][j]>r)?(1):(0); // S[i][j] = rate_edis(a[i],b[j]), D[i][j]=(S[i][j]>r)?(1):(0); // Line LCS match cout<<"That's ok LCS matching"<<endl; vector<vector<int>> sim_ab = lcs_str(D); cout<<endl; cout<<left<<setw(30)<<"a.cpp Matching code"; cout<<" "; cout<<left<<setw(30)<<"b.cpp Matching code"<<endl; for(int i=0; i<sim_ab.size(); i++) { cout<<left<<setw(30)<<a[sim_ab[i][0]]; cout<<" "; cout<<left<<setw(30)<<b[sim_ab[i][1]]<<endl; } double ra = (double)sim_ab.size() / (double)(min(a.size(), b.size())); cout<<endl<<"The matching rate is: "<<ra<<endl; cout<<endl<<"--------------------------------"<<endl<<endl; // Violent match cout<<"Violent match"<<endl; sim_ab = violate_match(S, r); cout<<endl; cout<<left<<setw(30)<<"a.cpp Matching code"; cout<<" "; cout<<left<<setw(30)<<"b.cpp Matching code"<<endl; for(int i=0; i<sim_ab.size(); i++) { cout<<left<<setw(30)<<a[sim_ab[i][0]]; cout<<" "; cout<<left<<setw(30)<<b[sim_ab[i][1]]<<endl; } ra = (double)sim_ab.size() / (double)(min(a.size(), b.size())); cout<<endl<<"The matching rate is: "<<ra<<endl; cout<<endl<<"--------------------------------"<<endl<<endl; /* // Map matching of variable relationship vector<string> a, b; // read source file readfile("a4.cpp", a); cout<<"a.cpp Original code: "< endl; print (a); cout < < endl; // Line filter code line_trim(a); cout<<"aaa.cpp Code after filtering: "< endl; print (a); cout < < endl; // Extract variables vector<string> a_vars = get_var(a); cout<<"aaa.cpp Variable extraction: "< endl; print (a)_ vars); cout<<endl; // Variable relation building vector<vector<int>> adj_a = get_var_adj(a, a_vars); cout<<endl<<"--------------------------------"<<endl<<endl; // read source file readfile("b4.cpp", b); cout<<"bbb.cpp Original code: "< endl; print (b); cout < < endl; // Line filter code line_trim(b); cout<<"bbb.cpp Code after filtering: "< endl; print (b); cout < < endl; // Extract variables vector<string> b_vars = get_var(b); cout<<"b.cpp Variable extraction: "< endl; print (b)_ vars); cout<<endl; // Variable relation building vector<vector<int>> adj_b = get_var_adj(b, b_vars); int cc = 0; for(int i=0; i<adj_b.size(); i++) { int cnt = 0; for(int j=0; j<adj_b.size(); j++) cnt+=adj_a[i][j]; if(cnt==0) continue; for(int j=0; j<adj_b.size(); j++) { #define R 0.88 if(cos_sim(adj_a[i], adj_b[j]) > R) { for(int r=0; r<a.size(); r++) { int v1aidx = a[r].find(a_vars[i]); int v2aidx = a[r].find(a_vars[j]); int v1bidx = b[r].find(b_vars[i]); int v2bidx = b[r].find(b_vars[j]); if(v1aidx!=string::npos && v2aidx!=string::npos && v1bidx!=string::npos && v2bidx!=string::npos) { cout<<left<<setw(55)<<a[r]; cout<<" -- "; cout<<left<<setw(55)<<b[r]<<endl; cc++; } } } } } cout<<"The matching rate is "< double) CC / min (a.size(), b.size()) / 2 < < endl; cout<<endl<<"--------------------------------"<<endl<<endl; */ return 0; } /* a12cd3kc 123kkkc abcadc cabedab */