Hello, everyone! In the previous article, we introduced three automatic optimal bin separation methods commonly used in the industry. 1) Optimal bin separation of continuous variables based on CART algorithm 2) Optimal bin division of continuous variables based on Chi square test 3) Continuous variable optimal bin division based on optimal KS Today's article will share the Python implementation of these three methods.
00 Index
01 preparation of test data and evaluation methods 02 implementation of optimal bin division code based on CART algorithm 03 implementation of optimal bin division code based on Chi square test 04 implementation of optimal bin division code based on optimal KS 05 test effect and section
01 preparation of test data and evaluation methods
In order to simulate the data sets we often encounter in risk modeling, I have simply created some data here, mainly including three columns:
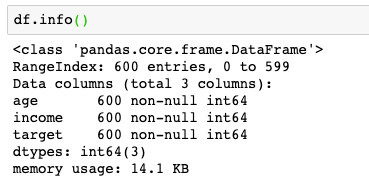
Among them, target is our Y column, and the other two are X column, which is our feature. What we need to do is to import data into the data set, which can be returned to cut in the background of official account (SamShare).
# Import related libraries
import pandas as pd
import numpy as np
import random
import math
from scipy.stats import chi2
import scipy
# Test data structure, where target is Y, 1 represents bad people and 0 represents good people.
df = pd.read_csv('./autocut_testdata.csv')
print(len(df))
print(df.target.value_counts()/len(df))
print(df.head())
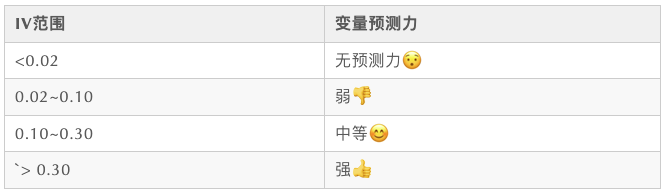
In addition, we need a method to evaluate the effect of box division. In the previous article, we mentioned that the effect can be measured by IV value, so we also need to construct a calculation method of IV value.
def iv_count(data, var, target):
''' calculation iv value
Args:
data: DataFrame,Data set to be operated
var: String,Quasi calculation IV Variable name of the value
target: String,Y Column name
Returns:
IV Value, float
'''
value_list = set(list(np.unique(data[var])))
iv = 0
data_bad = pd.Series(data[data[target]==1][var].values, index=data[data[target]==1].index)
data_good = pd.Series(data[data[target]==0][var].values, index=data[data[target]==0].index)
len_bad = len(data_bad)
len_good = len(data_good)
for value in value_list:
# Judge whether a certain class is 0 to avoid infinitesimal value and infinity value
if sum(data_bad == value) == 0:
bad_rate = 1 / len_bad
else:
bad_rate = sum(data_bad == value) / len_bad
if sum(data_good == value) == 0:
good_rate = 1 / len_good
else:
good_rate = sum(data_good == value) / len_good
iv += (good_rate - bad_rate) * math.log(good_rate / bad_rate,2)
# print(value,iv)
return iv
02 implementation of optimal bin division code based on CART algorithm
The implementation steps of continuous variable optimal bin division based on CART algorithm are as follows: 1. Given the continuous variable V, sort the values in V; 2. Successively calculate the Gini index of the median between adjacent elements as the binary division point; 3. Select the optimal division point (the Gini index decreases the most after division) as the division point of this iteration; 4. Recursively iterate steps 2-3 until the stop condition is met. (generally, the divided sample size is taken as the stop condition, for example, the sample size of leaf node > = 10% of the total sample size)
def get_var_median(data, var):
""" Gets the median list of all elements of the specified continuous variable
Args:
data: DataFrame,Data set to be operated
var: String,Name of continuous variable to be divided into boxes
Returns:
For a median list of all elements of a continuous variable, List
"""
var_value_list = list(np.unique(data[var]))
var_median_list = []
for i in range(len(var_value_list)-1):
var_median = (var_value_list[i] + var_value_list[i+1]) / 2
var_median_list.append(var_median)
return var_median_list
def calculate_gini(y):
""" Calculate Gini index
Args:
y: Array,Data to be calculated target,That is, an array of 0 and 1
Returns:
Gini index, float
"""
# Convert array to list
y = y.tolist()
probs = [y.count(i)/len(y) for i in np.unique(y)]
gini = sum([p*(1-p) for p in probs])
return gini
def get_cart_split_point(data, var, target, min_sample):
""" Obtain the optimal binary partition point (i.e. the point where the Gini index decreases the most)
Args:
data: DataFrame,Quasi operational data set
var: String,Name of continuous variable to be divided into boxes
target: String,Y Column name
min_sample: int,The minimum data sample of the sub box, that is, the amount of data at least reaches, which is generally used at the sub box point at the beginning or end
Returns:
BestSplit_Point: Return the optimal division point of this iteration, float
BestSplit_Position: Returns the position of the optimal dividing point, with 0 on the leftmost and 1 on the rightmost, float
"""
# initialization
Gini = calculate_gini(data[target].values)
Best_Gini = 0.0
BestSplit_Point = -99999
BestSplit_Position = 0.0
median_list = get_var_median(data, var) # Gets a list of all median values for the specified element of the current dataset
for i in range(len(median_list)):
left = data[data[var] < median_list[i]]
right = data[data[var] > median_list[i]]
# If the amount of data after segmentation is less than the specified threshold, skip the box splitting calculation
if len(left) < min_sample or len(right) < min_sample:
continue
Left_Gini = calculate_gini(left[target].values)
Right_Gini = calculate_gini(right[target].values)
Left_Ratio = len(left) / len(data)
Right_Ratio = len(right) / len(data)
Temp_Gini = Gini - (Left_Gini * Left_Ratio + Right_Gini * Right_Ratio)
if Temp_Gini > Best_Gini:
Best_Gini = Temp_Gini
BestSplit_Point = median_list[i]
# Get the position of the syncopation point. The leftmost is 0 and the rightmost is 1
if len(median_list) > 1:
BestSplit_Position = i / (len(median_list) - 1)
else:
BestSplit_Position = i / len(len(median_list))
else:
continue
Gini = Gini - Best_Gini
# print("optimal tangent point:", BestSplit_Point)
return BestSplit_Point, BestSplit_Position
def get_cart_bincut(data, var, target, leaf_stop_percent=0.05):
""" Calculate the optimal dividing point
Args:
data: DataFrame,Data set to be operated
var: String,Name of continuous variable to be divided into boxes
target: String,Y Column name
leaf_stop_percent: The proportion of leaf nodes, as the stop condition, is 5 by default%
Returns:
best_bincut: The best list of syncopation points, List
"""
min_sample = len(data) * leaf_stop_percent
best_bincut = []
def cutting_data(data, var, target, min_sample, best_bincut):
split_point, position = get_cart_split_point(data, var, target, min_sample)
if split_point != -99999:
best_bincut.append(split_point)
# The data set is segmented according to the optimal segmentation point, and the segmentation point is calculated recursively for the segmented data set until the stop condition is met
# print("the value range of this sub box is {0} ~ {1}". Format (data [var]. Min(), data [var] max()))
left = data[data[var] < split_point]
right = data[data[var] > split_point]
# When the data set after segmentation is still larger than the minimum data sample requirements, continue segmentation
if len(left) >= min_sample and position not in [0.0, 1.0]:
cutting_data(left, var, target, min_sample, best_bincut)
else:
pass
if len(right) >= min_sample and position not in [0.0, 1.0]:
cutting_data(right, var, target, min_sample, best_bincut)
else:
pass
return best_bincut
best_bincut = cutting_data(data, var, target, min_sample, best_bincut)
# Fill in the head and tail of the syncopation point
best_bincut.append(data[var].min())
best_bincut.append(data[var].max())
best_bincut_set = set(best_bincut)
best_bincut = list(best_bincut_set)
best_bincut.remove(data[var].min())
best_bincut.append(data[var].min()-1)
# Sort cut point
best_bincut.sort()
return best_bincut
03 implementation of optimal bin division code based on Chi square test
The implementation steps of continuous variable optimal bin division based on Chi square test are as follows: 1. Given the continuous variable V, sort the values in V, and then set each element value separately to complete the initialization phase; 2. For adjacent groups, calculate the chi square value in pairs; 3. Merge the two groups with the lowest chi square value; 4. Recursively iterate steps 2-3 until the stop condition is met. (generally, the chi square value is higher than the set threshold, or reaches the maximum number of groups, etc.)
def calculate_chi(freq_array):
""" Calculate chi square value
Args:
freq_array: Array,Two dimensional array of chi square value to be calculated, frequency statistics results
Returns:
Chi square value, float
"""
# Check whether it is a two-dimensional array
assert(freq_array.ndim==2)
# Calculate the sum of the frequencies of each column
col_nums = freq_array.sum(axis=0)
# Calculate the sum of the frequencies of each line
row_nums = freq_array.sum(axis=1)
# Calculate the total frequency
nums = freq_array.sum()
# Calculate the expected frequency
E_nums = np.ones(freq_array.shape) * col_nums / nums
E_nums = (E_nums.T * row_nums).T
# Calculate chi square value
tmp_v = (freq_array - E_nums)**2 / E_nums
# If the expected frequency is 0, the calculation result is recorded as 0
tmp_v[E_nums==0] = 0
chi_v = tmp_v.sum()
return chi_v
def get_chimerge_bincut(data, var, target, max_group=None, chi_threshold=None):
""" Calculate the optimal bin division point of chi square bin Division
Args:
data: DataFrame,Data set of the optimal cut-off point list of chi square sub box to be calculated
var: Name of continuous variable to be calculated
target: Target column to be calculated Y Name of
max_group: Maximum number of sub boxes (because chi square sub box is actually a process of merging boxes, the maximum number of sub boxes that can be retained needs to be limited)
chi_threshold: Chi square threshold, if not specified max_group,We select the number of categories by default-1,Confidence 95%To set the threshold
If you don't know how to get the chi square threshold, you can generate a chi square table to see the code as follows:
import pandas as pd
import numpy as np
from scipy.stats import chi2
p = [0.995, 0.99, 0.975, 0.95, 0.9, 0.5, 0.1, 0.05, 0.025, 0.01, 0.005]
pd.DataFrame(np.array([chi2.isf(p, df=i) for i in range(1,10)]), columns=p, index=list(range(1,10)))
Returns:
List of optimal tangent points, List
"""
freq_df = pd.crosstab(index=data[var], columns=data[target])
# Convert to 2D array
freq_array = freq_df.values
# Initialize the box, and each element has a separate group
best_bincut = freq_df.index.values
# Initialization threshold chi_threshold, if Chi is not specified_ Threshold, the number of target s is - 1 by default, and the confidence is 95%
if max_group is None:
if chi_threshold is None:
chi_threshold = chi2.isf(0.05, df = freq_array.shape[-1])
# Start iteration
while True:
min_chi = None
min_idx = None
for i in range(len(freq_array) - 1):
# Calculate the chi square values of two adjacent groups in pairs to obtain the two groups with the minimum chi square value
v = calculate_chi(freq_array[i: i+2])
if min_chi is None or min_chi > v:
min_chi = v
min_idx = i
# Whether to continue iterative condition judgment
# Condition 1: the current number of boxes is still greater than the threshold of the maximum number of boxes
# Condition 2: the current minimum chi square value is still less than the specified chi square threshold
if (max_group is not None and max_group < len(freq_array)) or (chi_threshold is not None and min_chi < chi_threshold):
tmp = freq_array[min_idx] + freq_array[min_idx+1]
freq_array[min_idx] = tmp
freq_array = np.delete(freq_array, min_idx+1, 0)
best_bincut = np.delete(best_bincut, min_idx+1, 0)
else:
break
# Fill in the head and tail of the syncopation point
best_bincut = best_bincut.tolist()
best_bincut.append(data[var].min())
best_bincut.append(data[var].max())
best_bincut_set = set(best_bincut)
best_bincut = list(best_bincut_set)
best_bincut.remove(data[var].min())
best_bincut.append(data[var].min()-1)
# Sort cut point
best_bincut.sort()
return best_bincut
04 implementation of optimal bin division code based on optimal KS
The implementation steps of continuous variable optimal bin division based on optimal KS are as follows: 1. Given the continuous variable V, sort the values in V; 2. Each element value is a calculation point, corresponding to bin0 ~ 9 in the above figure; 3. Calculate the element with the largest KS as the optimal division point, and divide the variable into two parts D1 and D2; 4. Recursively iterate step 3 and calculate the partition points of data set D1 and D2 generated in step 3 until the stop conditions are met. (generally, the number of boxes reaches a certain threshold, or the KS value is less than a certain threshold)
def get_maxks_split_point(data, var, target, min_sample=0.05):
""" calculation KS value
Args:
data: DataFrame,Data set of the optimal cut-off point list of chi square sub box to be calculated
var: Name of continuous variable to be calculated
target: Target column to be calculated Y Name of
min_sample: int,The minimum data sample of the sub box, that is, the amount of data at least reaches, which is generally used at the sub box point at the beginning or end
Returns:
ks_v: KS Value, float
BestSplit_Point: Return the optimal division point of this iteration, float
BestSplit_Position: Returns the position of the optimal dividing point, with 0 on the leftmost and 1 on the rightmost, float
"""
if len(data) < min_sample:
ks_v, BestSplit_Point, BestSplit_Position = 0, -9999, 0.0
else:
freq_df = pd.crosstab(index=data[var], columns=data[target])
freq_array = freq_df.values
if freq_array.shape[1] == 1: # If a group has only one enumeration value, such as 0 or 1, the array shape will have problems and jump out of this calculation
# tt = np.zeros(freq_array.shape).T
# freq_array = np.insert(freq_array, 0, values=tt, axis=1)
ks_v, BestSplit_Point, BestSplit_Position = 0, -99999, 0.0
else:
bincut = freq_df.index.values
tmp = freq_array.cumsum(axis=0)/(np.ones(freq_array.shape) * freq_array.sum(axis=0).T)
tmp_abs = abs(tmp.T[0] - tmp.T[1])
ks_v = tmp_abs.max()
BestSplit_Point = bincut[tmp_abs.tolist().index(ks_v)]
BestSplit_Position = tmp_abs.tolist().index(ks_v)/max(len(bincut) - 1, 1)
return ks_v, BestSplit_Point, BestSplit_Position
def get_bestks_bincut(data, var, target, leaf_stop_percent=0.05):
""" Calculate the optimal dividing point
Args:
data: DataFrame,Data set to be operated
var: String,Name of continuous variable to be divided into boxes
target: String,Y Column name
leaf_stop_percent: The proportion of leaf nodes, as the stop condition, is 5 by default%
Returns:
best_bincut: The best list of syncopation points, List
"""
min_sample = len(data) * leaf_stop_percent
best_bincut = []
def cutting_data(data, var, target, min_sample, best_bincut):
ks, split_point, position = get_maxks_split_point(data, var, target, min_sample)
if split_point != -99999:
best_bincut.append(split_point)
# The data set is segmented according to the optimal segmentation point, and the segmentation point is calculated recursively for the segmented data set until the stop condition is met
# print("the value range of this sub box is {0} ~ {1}". Format (data [var]. Min(), data [var] max()))
left = data[data[var] < split_point]
right = data[data[var] > split_point]
# When the data set after segmentation is still larger than the minimum data sample requirements, continue segmentation
if len(left) >= min_sample and position not in [0.0, 1.0]:
cutting_data(left, var, target, min_sample, best_bincut)
else:
pass
if len(right) >= min_sample and position not in [0.0, 1.0]:
cutting_data(right, var, target, min_sample, best_bincut)
else:
pass
return best_bincut
best_bincut = cutting_data(data, var, target, min_sample, best_bincut)
# Fill in the head and tail of the syncopation point
best_bincut.append(data[var].min())
best_bincut.append(data[var].max())
best_bincut_set = set(best_bincut)
best_bincut = list(best_bincut_set)
best_bincut.remove(data[var].min())
best_bincut.append(data[var].min()-1)
# Sort cut point
best_bincut.sort()
return best_bincut
05 test effect and section
Well, we have also implemented the above three methods of dividing boxes of continuous variables in Python. Let's test the effect right away.
df['age_bins1'] = pd.cut(df['age'], bins=get_cart_bincut(df, 'age', 'target'))
df['age_bins2'] = pd.cut(df['age'], bins=get_chimerge_bincut(df, 'age', 'target'))
df['age_bins3'] = pd.cut(df['age'], bins=get_bestks_bincut(df, 'age', 'target'))
print("variable age The results are as follows:")
print("age_cart_bins:", get_cart_bincut(df, 'age', 'target'))
print("age_chimerge_bins:", get_chimerge_bincut(df, 'age', 'target'))
print("age_bestks_bins:", get_bestks_bincut(df, 'age', 'target'))
print("IV The values are as follows:")
print("age:", iv_count(df, 'age', 'target'))
print("age_cart_bins:", iv_count(df, 'age_bins1', 'target'))
print("age_chimerge_bins:", iv_count(df, 'age_bins2', 'target'))
print("age_bestks_bins:", iv_count(df, 'age_bins3', 'target'))
df['income_bins1'] = pd.cut(df['income'], bins=get_cart_bincut(df, 'income', 'target'))
df['income_bins2'] = pd.cut(df['income'], bins=get_chimerge_bincut(df, 'income', 'target'))
df['income_bins3'] = pd.cut(df['income'], bins=get_bestks_bincut(df, 'income', 'target'))
print("variable income The results are as follows:")
print("income_cart_bins:", get_cart_bincut(df, 'income', 'target'))
print("income_chimerge_bins:", get_chimerge_bincut(df, 'income', 'target'))
print("income_bestks_bins:", get_bestks_bincut(df, 'income', 'target'))
print("IV The values are as follows:")
print("income:", iv_count(df, 'income', 'target'))
print("income_cart_bins:", iv_count(df, 'income_bins1', 'target'))
print("income_chimerge_bins:", iv_count(df, 'income_bins2', 'target'))
print("income_bestks_bins:", iv_count(df, 'income_bins3', 'target'))


We can see from it that the effects of the three different box splitting methods are still somewhat different, but one thing in common is that the IV value is smaller than that in front of the box. After all, it is reasonable to sacrifice some "IV" for efficiency. In the actual modeling, I usually use three methods directly to select the one with the best box separation effect. The above is a relatively simple implementation. You are also welcome to try. You can give random feedback on any problems
Reference
https://blog.csdn.net/xgxyxs/article/details/90413036 https://zhuanlan.zhihu.com/p/44943177 https://blog.csdn.net/hxcaifly/article/details/84593770 https://blog.csdn.net/haoxun12/article/details/105301414/ https://www.bilibili.com/read/cv12971807