Portal

General idea of the topic

A weighted tree is given, in which the weight of all parent nodes must be strictly greater than that of child nodes. The weights of all leaf nodes and the nearest common ancestor between two leaves are given L C A LCA The weight of LCA, try to restore this tree.

Problem solving ideas

The construction of trees is mostly from special to general, starting from leaf nodes.

For two leaf nodes, it is obvious that the first operation only needs to create a new node, and then connect them; For two subtrees with two leaf nodes connected respectively, as shown in the figure below, if 1    4 1~~4 1 # 4 L C A LCA The weight of LCA is greater than two parent nodes 5 , 6 5,6 5,6, then let's build a new one 7 7 7 nodes connect the two subtrees.

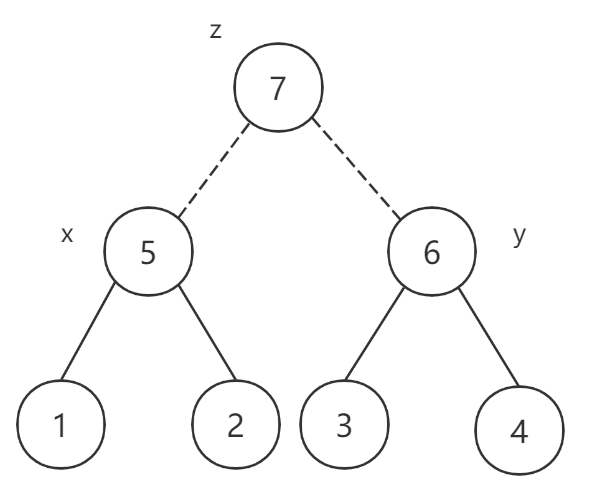
At this time, it seems that the structural law can be seen. For each pair of given L C A LCA LCA information, from small to large. There will be two situations for the above subtree, that is, the current subtree L C A LCA LCA is equal to a root node of two subtrees, then connect the other subtree. As for how to maintain the root node of a subtree, use the joint query set, but the joint query set only maintains two sets. How to ensure that the ancestor of the set is the root node? In fact, you only need to set the ancestor of the current set to be updated as the root node, so that the information of the ancestor node will not change when the path is compressed, and only the ancestor node of the child node below will be updated. What a wonderful use!

Error prone point: if there are many nodes under the subtree of a node, how to ensure that two identical parent nodes are not generated (for the greedy idea of this topic, make the same as far as possible) L C A LCA LCA is connected to the same root node), then for the same L C A LCA LCA weights are sorted in ascending order according to the nodes with smaller sequence number, and then in ascending order according to the nodes with larger sequence number. for example 1    2    3    4 1~~2~~3~~4 1 # 2 # 3 # 4 L C A LCA LCA S are the same, obviously 1    2 1~~2 1  2, 1    3 1~~3 1  3, 1    4 1~~4 1 # 4... The above problems will not occur in this way.

reference: https://blog.csdn.net/liufengwei1/article/details/114298063

#include <bits/stdc++.h>

using namespace std;
#define ENDL "\n"
typedef long long ll;
const int maxn = 5e5 + 10;

struct node {
    int u, v, w;

    bool operator<(const node &p) const {
        if (w == p.w) {
            if (u == p.u) return v < p.v;
            return u < p.u;
        }
        return w < p.w;
    }
};

vector<node> res;
int f[maxn], father[maxn], val[maxn];

int Find(int x) { return f[x] == x ? x : f[x] = Find(f[x]); }

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    for (int i = 1; i <= n * n; i++) f[i] = i;
    for (int i = 1, x; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cin >> x;
            if (j > i)
                res.push_back({i, j, x});
            else if (i == j)
                val[i] = x;
        }
    }
    sort(res.begin(), res.end());
    int idx = n + 1;
    for (auto p : res) {
        int fu = Find(p.u), fv = Find(p.v);
        if (fu == fv) continue;
        int Max = max(val[fu], val[fv]);
        if (Max == p.w) {
            if (p.w == val[fu])
                father[fv] = f[fv] = fu;
            else
                father[fu] = f[fu] = fv;
        } else {
            father[fu] = father[fv] = idx;
            val[idx] = p.w;
            f[fu] = f[fv] = idx;
            idx++;
        }
    }
    cout << idx - 1 << ENDL << val[1];
    for (int i = 2; i <= idx - 1; i++) cout << ' ' << val[i];
    cout << ENDL;
    cout << idx - 1 << ENDL;
    for (int i = 1; i <= idx - 2; i++) {
        if (father[i]) cout << i << " " << father[i] << ENDL;
    }
    return 0;
}