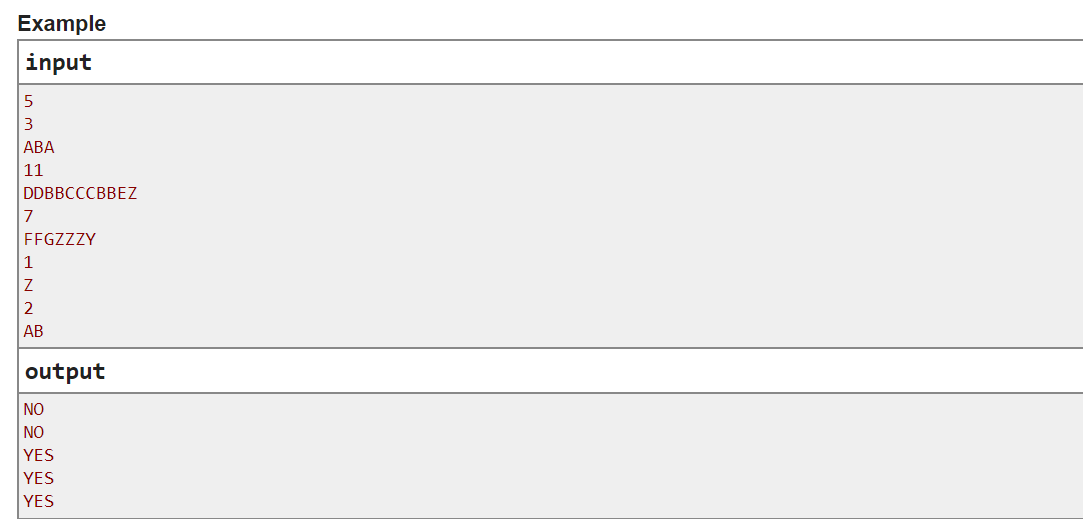
A. Do Not Be Distracted!
Original title link: https://codeforces.ml/contest/1520/problem/A
General idea of the topic
If such as aaaaadddbbfgh, each letter appears only once continuously, then YES is output; otherwise, if such A as AABBA appears twice or more continuously in different positions, NO is output
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <unordered_set>
#include <unordered_map>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define ull unsigned long long
#define PII pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 100;
char str[N];
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
rit;
while (t --) {
rin;
getchar();
sc("%s", str);
getchar();
int book[26] = {0};
bool flag = true; //flag is false, which means it appears twice or more in a row
for (int i = 0; i < n; ++ i) {
int a = str[i] - 'A';
int j = i + 1;
while (j < n && str[j] == str[i]) ++ j; //Skip consecutive identical parts
i = j - 1;
if (book[a]) {
flag = false;
break;
}
++ book[a];
}
if (flag) pr("YES\n");
else pr("NO\n");
}
return 0;
}
B. Ordinary Numbers
Original title link: https://codeforces.ml/contest/1520/problem/B
General idea of the topic
If the numbers on each bit of a number are consistent, it is called an ordinary number, such as 1, 99, 111, etc
Please calculate the number of ordinary numbers from 1 to n

thinking
Obviously, there are 9 ordinary numbers in all single digits, 9 ordinary numbers in all two digits and 9 ordinary numbers in all three digits
Then, for a number 9876, we can first get that it is a four digit number, then for one digit, two digit and three digit number, there can be 3 * 9 = 27 ordinary numbers
Since the highest bit of 9876 is 9, there will be at least 9 - 1 ordinary numbers in all four digits, and since 9876 < 9999, there is no need to add another one
To sum up, there are between. 76 and. 981 ordinary
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <unordered_set>
#include <unordered_map>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define ull unsigned long long
#define PII pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
//Get the number of digits of n
int dswei(int n) {
int ans = 0;
while (n > 0) {
++ ans;
n /= 10;
}
return ans;
}
//Obtain the highest digit of N, where n is a total of a digits
int zgwei(int n, int a) {
return n / (int)(pow(10, a - 1));
}
//Get the number consisting of a and b
int hdzhi(int b, int a) {
int ans = 0;
while (a --) {
ans = ans * 10 + b;
}
return ans;
}
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
rit;
while (t --) {
rin;
int a = dswei(n);
int ans = (a - 1) * 9;
int b = zgwei(n, a);
ans += b - 1;
if (n >= hdzhi(b, a)) ans ++;
pr("%d\n", ans);
}
return 0;
}
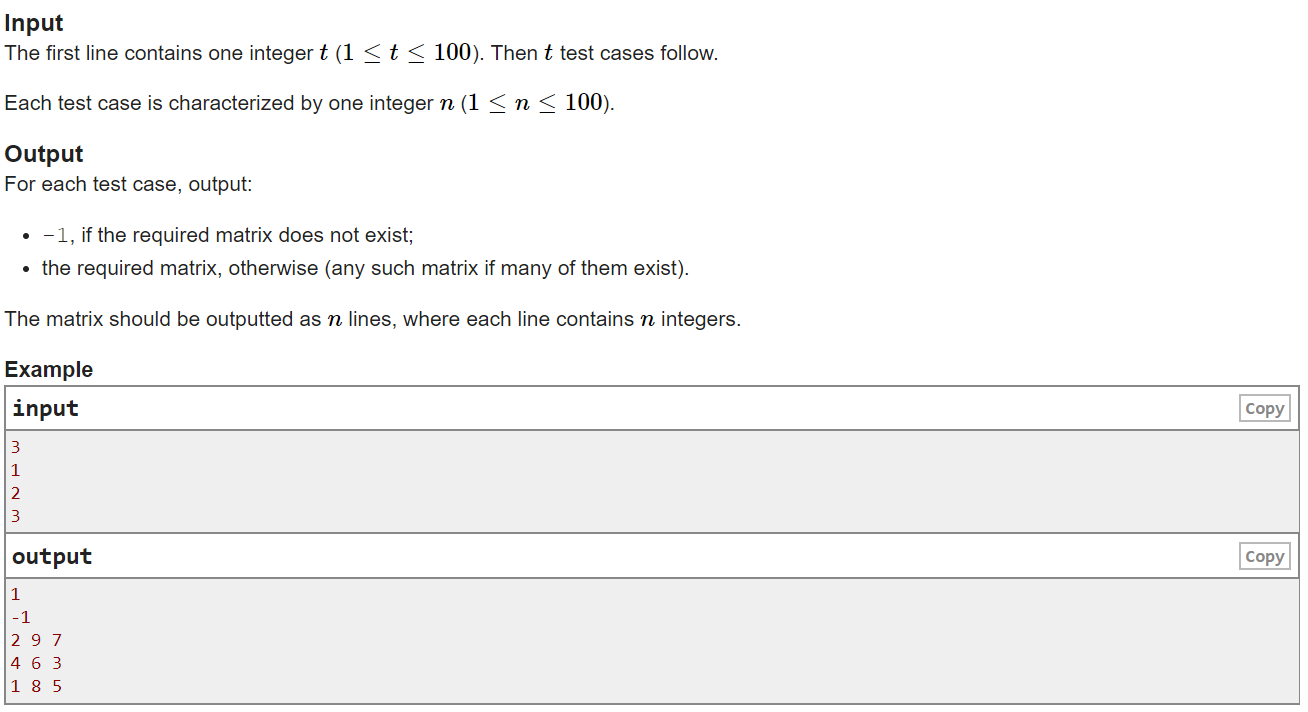
C. Not Adjacent Matrix
Original title link: https://codeforces.ml/contest/1520/problem/C
General idea of the topic
Construct an n * n matrix, in which the number of each bit of the matrix is in the range of 1 to n * n, and each number can only be used once
At the same time, the absolute value of each number in the matrix and its upper, lower, left and right numbers must be greater than 1
If such a matrix cannot be constructed, output - 1, otherwise output the matrix
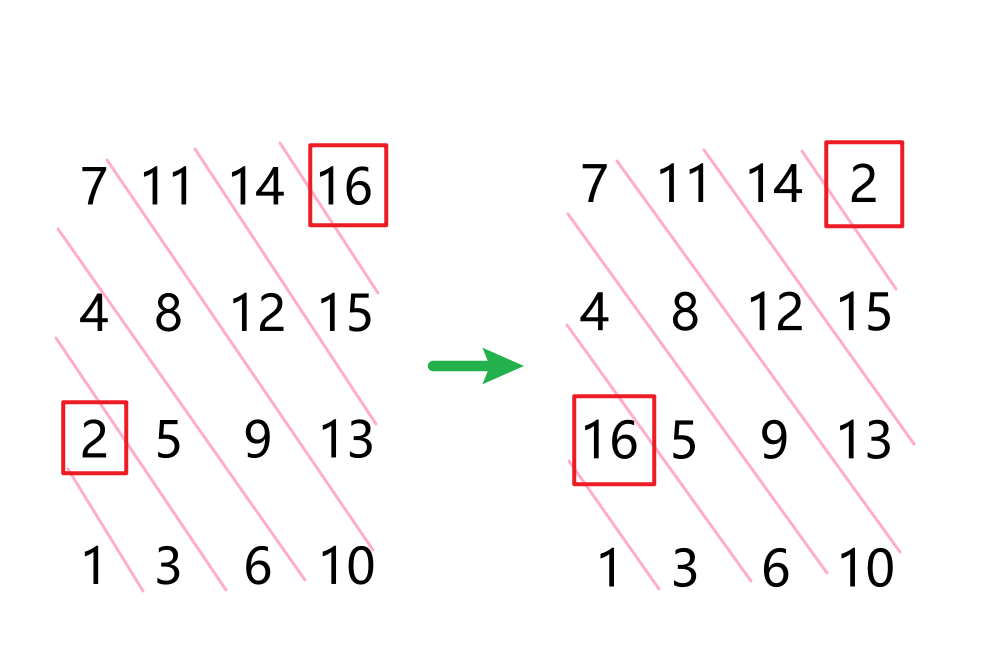
thinking
Obviously, the numbers with adjacent values cannot be placed in two adjacent cells. There should be many filling methods for this problem. Here I mainly fill them obliquely. Finally, I can change the position of 2 and n * n See the following figure for details:
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <unordered_set>
#include <unordered_map>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define ull unsigned long long
#define PII pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 110;
int ans[N][N];
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
rit;
while (t --) {
rin;
if (n == 1) pr("1\n");
else if (n == 2) pr("-1\n"); //All but 2 can construct matrices
else {
int cnt = 1; //Counter filled with numbers
//Fill 1 to diagonal number
for (int i = n; i >= 1; -- i) {
int x = i, y = 1;
while (x >= 1 && x <= n && y >= 1 && y <= n) {
ans[x][y] = cnt ++;
++ x;
++ y;
}
}
//Fill diagonal to n * n
for (int i = 2; i <= n; ++ i) {
int x = 1, y = i;
while (x >= 1 && x <= n && y >= 1 && y <= n) {
ans[x][y] = cnt ++;
++ x;
++ y;
}
}
//Output matrix
for (int i = 1; i <= n; ++ i) {
for (int j = 1; j <= n; ++ j) {
if (ans[i][j] == 2) pr("%d", n * n);
else if (ans[i][j] == n * n) pr("%d", 2);
else pr("%d", ans[i][j]);
if (j < n) pr(" ");
}
pr("\n");
}
}
}
return 0;
}
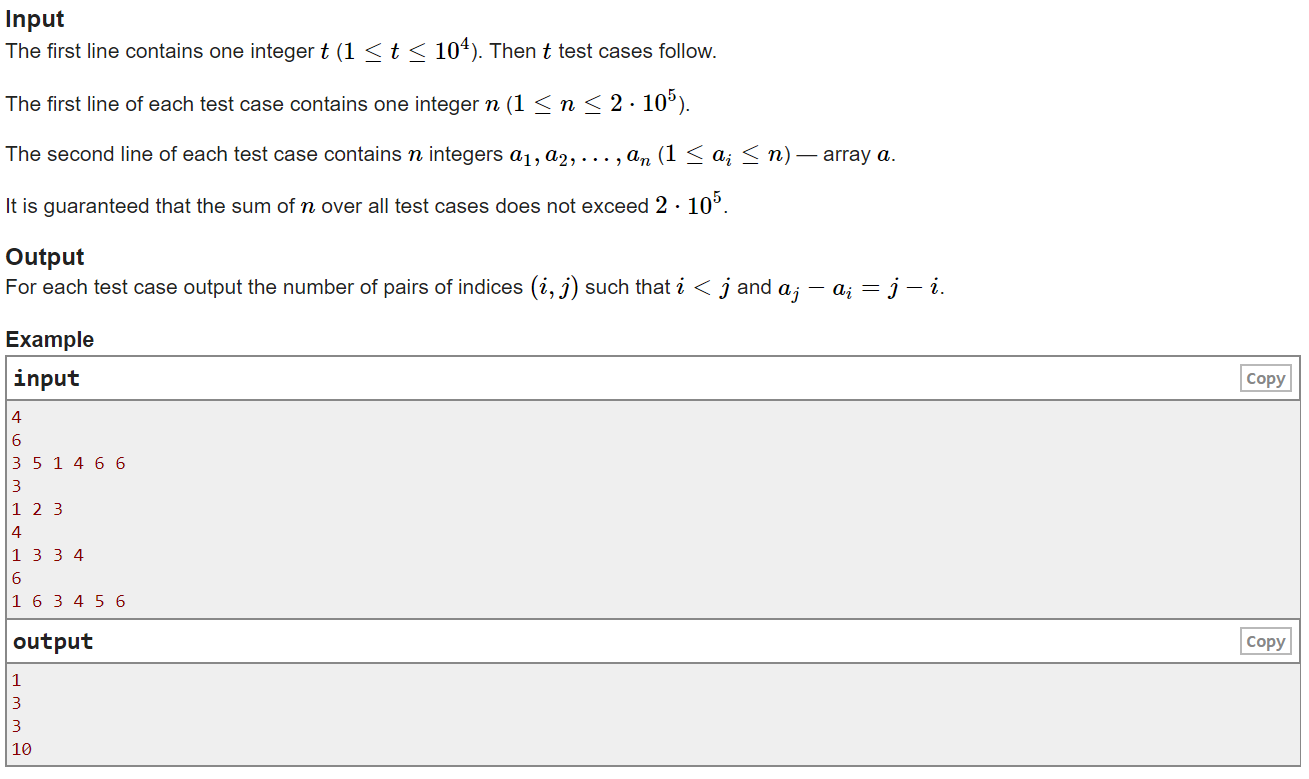
D. Same Differences
Original title link: https://codeforces.ml/contest/1520/problem/D
General idea of the topic
For a sequence with n numbers, find two numbers ai and aj satisfying i < J and aj − ai = j − i, and output the total number of pairs of such ai and aj in the sequence
thinking
Suppose there is a sequence of 1, 6, 3, 4, 5, 7
So obviously, there are only 1, x, 3, 4, 5 and X in this sequence, and the four numbers can form pairs that meet the requirements of the topic
x, 6, x, x, x, x and X, x, x, x, x, x, 7 cannot form pairs with other numbers
Here, we can add a counter at the head of the original sequence (the counter can be realized by hash table or array simulation, because the subject value is limited, it must be less than or equal to n). The significance of this counter is to calculate the starting value sequence of pairs that can be formed with 6
For example [counter + 1, 6, 3, 4, 5, 7], and the value of 1, x, 3, 4, 5, x in the counter is 0, because it starts with 0 to ensure strict monotonic increase. When encountering 1, ans + = map [0], map [0] +; When 3 is encountered, ans + = map [0], map [0] + +
Here, ans += map [0] means that since the index of 3 is 3, it must be the same number at the head of the queue 0 to form a legal pair with 3;
Map [0] + + indicates that a new member is added to the team with 0 as the team head. In the future, there will be one more team with 0 as the team head
The language may not be well expressed, but you can understand it as long as you simulate it manually according to the code
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <unordered_set>
#include <unordered_map>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define ull unsigned long long
#define PII pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 200010;
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
rit;
while (t --) {
rin;
ll ans = 0;
unordered_map<int, int> m;
for (int i = 1; i <= n; ++ i) {
ria;
ans += m[a - i];
++ m[a - i];
}
pr("%lld\n", ans);
}
return 0;
}
E. Arranging the sheet
Original title link: https://codeforces.ml/contest/1520/problem/E
General idea of the topic
If there is such a string of strings *. *. *. ** Represents sheep Stands for empty space. Now it is required to make all sheep gather together (there is no empty space between each other) under the minimum number of operations. As for aggregation * * Or Or any other form
thinking
When in position idx, we use L to indicate how many sheep there are to the left of idx and R to indicate how many sheep there are in idx
So for idx, if there are sheep in this position, then + + L, – R
If this position is empty, let the sheep on which side move one step in the opposite direction of this position
(
In fact, l represents how many groups have gathered on the left of idx at this time. If ans += L, it represents that the group on the left moves one step to the right as a whole;
In fact, R represents how many sheep on the right of idx may not be clustered yet, and ans += R, so this statement represents that it is very bad to move the whole group clustered on the left to the right. It is better to let the sheep that may still be scattered on the right move one step to the left in the original position. After all, as long as they all get together in the end, It doesn't matter which section you stop in
)
For example, for the sequence *. *. *. ** The whole process is as follows:
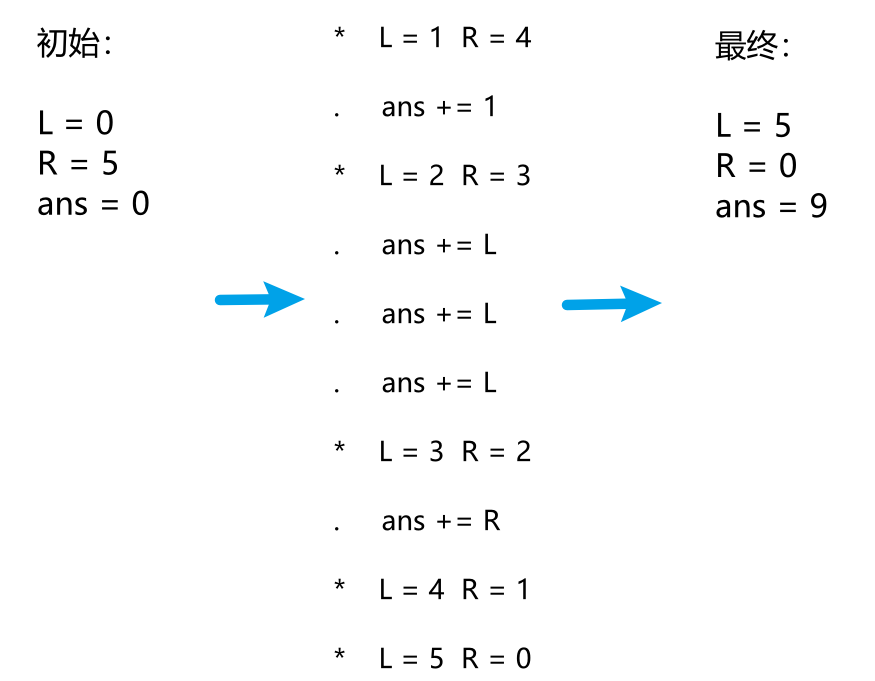
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
#include <unordered_set>
#include <unordered_map>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define ull unsigned long long
#define PII pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 1000010;
char str[N];
int main() {
freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
rit;
while (t --) {
rin;
getchar();
sc("%s", str);
ll ans = 0;
int l = 0, r = 0;
// Count sheep
for (int i = 0; i < n; ++ i) {
if (str[i] == '*')
++ r;
}
for (int i = 0; i < n; ++ i) {
if (str[i] == '*') {
++ l;
-- r;
}
else {
ans += min(l, r);
}
}
pr("%lld\n", ans);
}
return 0;
}