Distance tree

Limited ability, only understand easy version

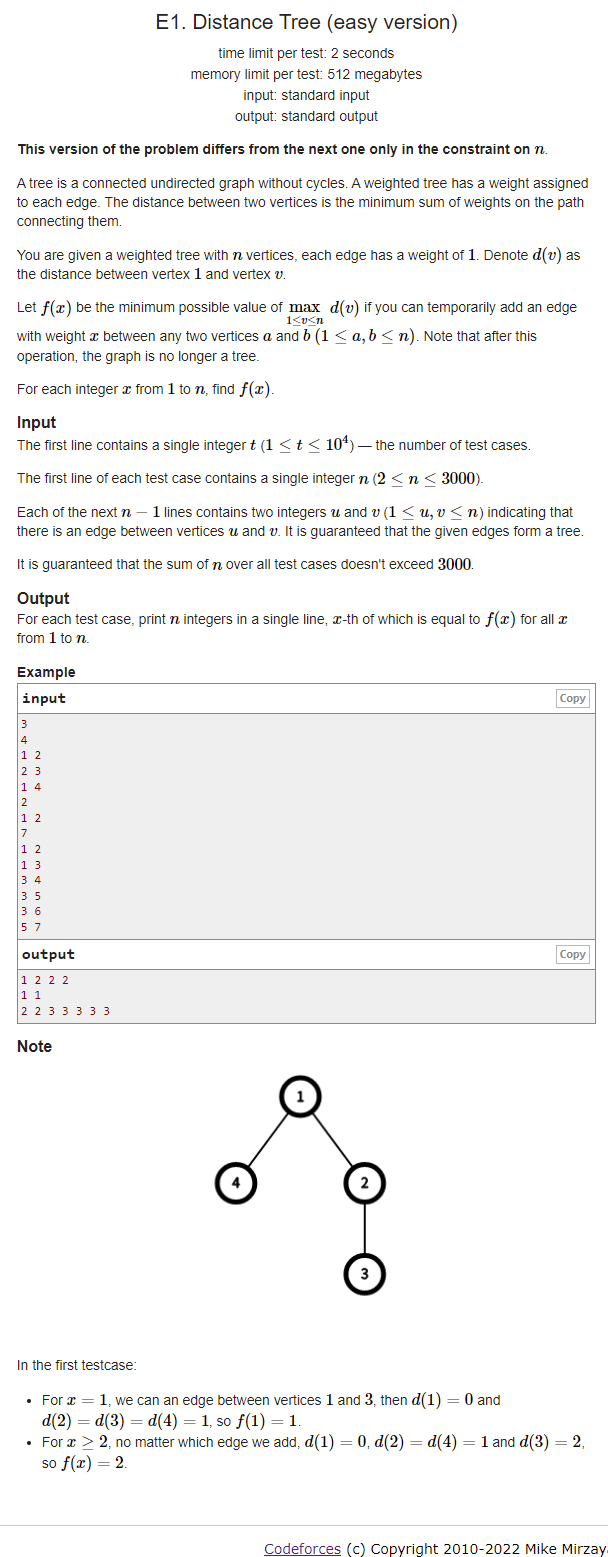
Meaning:

• Given a tree with n nodes, d ( v ) d(v) d(v) represents the shortest distance from any point to 1 point on the tree
• definition f ( x ) f(x) f(x) means: after adding an edge with weight X between any two points on the tree, M a x 1 < = v < = n d ( v ) Max_{1<=v<=n}d(v) Max1 < = V < = value of n d(v)
• For all x values from 1 to N, find the corresponding f ( x ) f(x) f(x)
• Analysis: how to add an edge to the tree to minimize the maximum value of the shortest distance from each point to 1 point

Idea:

• The optimal operation of edging is obviously a point connected to 1, which can be simulated on paper by itself;
• We should not only consider the limit point in the operation of edge adding, such as the point farthest from 1; It is inappropriate to only modify the distance from the farthest point to 1, regardless of the second farthest point and the second farthest point;
• In order to minimize the maximum value, we'd better put the edge point in the center of the tree. The shortest distance from each point to the point is relatively average. The meaning of the problem solution is so that it can't be proved in detail;

Based on the above premise, the problem solution gives a very necessary enumeration method - enumerating answers (there is no two points for the two-point answer)

We assume an ans answer every time, which means the distance from the point 1 after edge addition to the farthest point. If the edge addition point is on the center of the tree, because the center of the tree = = the midpoint of the tree diameter, we can know the diameter of the tree== 2 ∗ ( a n s − x ) 2*(ans-x) 2∗(ans−x)

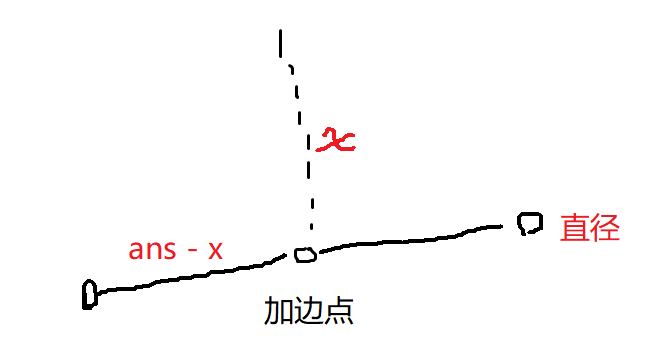
Under the limitation of this answer, we can determine whether the ans answer should be kept or increased (as small as possible) by finding the diameter of the tree

Is it similar to the two-point answer?

As for what restrictions are, they are:

• If the current ans == 2, when we calculate the diameter of the tree, we can't enumerate the points with depth dep (distance from 1 point) < = 2, that is, the points at both ends of the diameter can't be these points, because these points can go directly to 1 without affecting ANS. the placement of edge points is to give priority to the limit points at both ends of the diameter and reduce the distance from the limit point to 1
• It's a metaphysical explanation. There's a better explanation to exchange

Finally, the answer given by cf is O ( n 3 ) O(n^3) The personal test limit of O(n3) will be 4s by the chain tree data card, but the person who made the question doesn't seem to have produced this kind of data. If I make a mistake, please guide me

Here is a sort preprocessing and pointer traversal method, which is stable O ( n 2 ) O(n^2) O(n2)

C o d e : Code: Code:

#include<bits/stdc++.h>
#include<unordered_set>
#include<unordered_map>
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define sca scanf
#define pri printf
#define ul (u << 1)
#define ur (u << 1 | 1)
#define forr(a,b,c) for(int a=b;a<=c;a++)
#define rfor(a,b,c) for(int a=b;a>=c;a--)
//#define x first
//#define y second
//[blog address]( https://blog.csdn.net/weixin_51797626?t=1) 
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;

const int N = 3010, M = 6010, MM = N;
int INF = 0x3f3f3f3f, mod = 1e9 + 7;
ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, k, T, S, D;
int h[N], e[M], ne[M], idx;
int d1[N], depdis[N];
struct node
{
	int w, id;
	bool operator<(const node& no)const { return w > no.w; }
}dd[N];

inline void add(int a, int b) {
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int x, int fa, int* d) {
	for (int i = h[x]; ~i; i = ne[i]) {
		int j = e[i];
		if (j == fa)continue;
		d[j] = d[x] + 1;
		dfs(j, x, d);
	}
}

void solve() {
	cin >> n;
	idx = 0;
	forr(i, 1, n)h[i] = -1;//Be careful to initialize by data. Don't use memset indiscriminately

	forr(i, 1, n - 1) {
		int a, b;
		cin >> a >> b;
		add(a, b), add(b, a);
	}

	int d_dep = 1;//Record the farthest point from 1
	d1[1] = 0;
	dfs(1, -1, d1);
	forr(i, 1, n)if (d1[i] > d1[d_dep])d_dep = i;

	depdis[d_dep] = 0;
	dfs(d_dep, -1, depdis);//The distance from one other point to the farthest point

	forr(i, 1, n)dd[i] = { depdis[i],i };//Record with array
	sort(dd + 1, dd + 1 + n);//Sort from large to small
	//The biggest must be the diameter of the tree. If one end of the diameter is covered, it will be rounded off to find the second diameter

	forr(i, 1, n) {
		if (d1[d_dep] <= i) {//If the added side doesn't contribute, just leave
			cout << d1[d_dep] << ' ';
			continue;
		}
		int j = 1, ans = 0;//Otherwise, enumerate the answers
		while (1)
		{
			int max_dist = -1;
			//The diameter that is limited at this moment must also be limited when ans becomes larger, so the pointer can only run once without cycling
			while (j <= n) { 
				int id = dd[j].id;
				if (d1[id] <= ans)j++;//limit
				else {
					max_dist = dd[j].w;
					break;
				}
			}
			if (max_dist == -1)break;//If you can't find the description, you can't update ans, exit

			if (max_dist > 2 * (ans - i))ans++;
			else break;//Similarly
		}
		cout << ans << ' ';

		//Preprocessing can ensure that two while loops are independent
	}
	cout << '\n';
}

int main() {
	cinios;

	cin >> T;
	while (T--)solve();

	return 0;
}
/*
*/