| On the right side of the page, there is a directory index, which can jump to the content you want to see according to the title |
|---|
| If not on the right, look for the left |
1. Recognize time complexity
If the execution time of an operation is not transferred by the specific sample size, each execution time is a fixed time. Such operations are called constant time operations
- Operations with fixed execution time are constant time operations (for example, array values and operation time will not change due to the value with subscript 1 or subscript 10000. They are obtained directly from the address)
- Operations whose execution time is not fixed are not constant time operations (for example, when sorting a group of numbers, your algorithm needs to compare them one by one to get the correct results. The more the number, the longer the operation time, and it is not fixed)
- Common constant time operations

| Advantages and disadvantages of common evaluation algorithms |
|---|
- Time complexity (determined by process)
- Additional space complexity (process decision)
- Constant term time (determined by implementation details)
It is to study the execution times of constant time operation after the execution of the whole algorithm, so as to generate an expression
- When the expression is established, just leave the highest order term, remove the lower order term and the coefficient of the higher order term, and finally record it as O (ignore the highest order term of the coefficient)
- The reason why we should remove the coefficient is that we calculate an algorithm. Under any amount of data, the time complexity required and the size of the coefficient are meaningless
- It must be sorted according to the worst case, such as insertion sorting algorithm, 123456, sorting, no need to exchange positions, and the complexity is O(N). In the worst case, 654321, it must be full every time, which is O(N ^ 2). Then we only consider the worst case, and the insertion sorting time complexity is O(N ^ 2)
- But if you are a professional, there are actually three kinds of time complexity calculation, the best case (the symbol is Θ), The average case (sign Ω) and the worst case (sign O), but interview questions and daily calculations only estimate the worst case O
| Analyze the time complexity of selection sorting |
|---|
public class Main {
public static void main(String[] args) {
int arr[] = {10,4,5,2,3,7,11,26};
int minIndex;
//The main constant operation of this algorithm is comparison. We can calculate the number of comparisons
for(int i = 0;i<arr.length-1;i++){//i~n-1==a*n-1
minIndex = i;//Record minimum subscript
for (int j = i+1;j<arr.length;j++){//i+1~n==b*n
if(arr[minIndex]>arr[j]){
minIndex = j;
}
}
if(i != minIndex){
//change of position
arr[i] = arr[i]^arr[minIndex];//Obtaining the XOR result is equivalent to a third variable and a key. The key XOR arr[i] will get arr[minIndex], and the XOR arr[minIndex] will get arr[i]
arr[minIndex] = arr[i]^arr[minIndex];//The XOR result is XOR arr[minIndex] again to get arr[i]
arr[i] = arr[i]^arr[minIndex];//The XOR result is exclusive or arr[i] to get arr[minIndex]
}
}//Remove the coefficient (n-1)*(n)=n^2 - n, keep only the highest order term n^2, and finally record it as O(n^2)
for(int i = 0;i<arr.length;i++){
System.out.print(arr[i]+" ");
}
}
}
| Insert sort time complexity is also O(N^2) |
|---|
public class Main {
public static void main(String[] args) {
int arr[] = {10,4,5,2,3,7,11,26};
System.out.print("The original sequence is:"+arr[0]+" ");
//Insertion sorting is that subscripts 0 ~ 0 ensure order, 0 ~ 1 ensure order, 0 ~ 2 ensure order 0~i ensure order, and i is the number of elements to be sorted
//Insert sorting, 0 ~ 0 ordered, no row, directly row 0~i
for(int i = 1;i<=arr.length-1;i++){
System.out.print(arr[i]+" ");
for (int j = i-1;j >=0 && arr[j]>arr[j+1];j--){
arr[j] = arr[j]^arr[j+1];//Obtaining the XOR result is equivalent to a third variable and a key. The key XOR arr[i] will get arr[minIndex], and the XOR arr[minIndex] will get arr[i]
arr[j+1] = arr[j]^arr[j+1];//The XOR result is XOR arr[minIndex] again to get arr[i]
arr[j] = arr[j]^arr[j+1];//The XOR result is exclusive or arr[i] to get arr[minIndex]
}
}
System.out.print("\n After sorting:");
for(int i = 0;i<arr.length;i++){
System.out.print(arr[i]+" ");
}
}
}
| Additional space complexity |
|---|
- You need to implement an algorithm flow. In the process of implementing the algorithm flow, you need to open up some space to support your algorithm flow, which is the additional space complexity
- Some necessary or required by users, which are related to the realization of objectives but not required in the algorithm process, are not considered as additional space, such as:
- Space as input parameter
- Space as output result
- If your process needs to open up space to continue your process, this part is also additional space
- If your process only needs to open up a limited number of variables (for example, a total of 3 variables are required, if you are not sure how many, it is infinite), the additional space complexity is O(1)
- Because the indicator of time complexity ignores low-order terms and all constant coefficients, how about the processes with the same time complexity, such as selection sorting, bubble sorting and insertion sorting? Of course not
- If two algorithms with the same time complexity want to spell the higher one, the lower one, and the better one, they will enter the stage of spell constant time, which is called spell constant term for short
- Directly apply for large samples, actually run, and then observe the running time. Don't go to theoretical analysis, because it's not necessary to waste energy
| How to obtain the optimal solution |
|---|
- First, the time complexity should be as low as possible
- After meeting the time complexity, the optimal solution is to use the least space
- The constant term is relatively insignificant, because this factor only determines the optimization and consideration of the implementation level, and has nothing to do with the idea of how to solve the whole problem
| Common time complexity, ranking from small to large, the best is the first, and the worst is the last, |
|---|
- O(1): constant level algorithm
- O(logN): N based on 2 in the log
- O(N)
- O(N*logN)
- O(N ^ 2),O(N ^ 3)...,O(N ^ K)
- O(2 ^ N),O(3 ^ N)...,O(K ^ N)
- O(N!): Factorial of n
2. Backtracking
2.1 maze problem
- The ball is initially in the upper left corner of the maze, and find the path of the ball to the lower right corner

- Operation effect (1: represents the wall, 0: represents the open space, 2: represents the route of the ball)

- code
public class Test {
public static void main(String[] args) {
// First create a two-dimensional array to simulate the maze
// Map
int[][] map = new int[8][7];
// Use 1 for walls
// Set up and down to 1
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
// All left and right are set to 1
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
//Set baffle, 1 indicates
map[3][1] = 1;
map[3][2] = 1;
// Output map
System.out.println("Map situation");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
//Use recursive backtracking to find the way for the ball
setWay(map, 1, 1);
//Output a new map, the ball passes, and identifies the recursion
System.out.println("The ball walked past and marked the map");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
//Use recursive backtracking to find the way for the ball
//explain
//1. map means map
//2. i,j indicates where to start from on the map (1,1)
//3. If the ball can reach the map[6][5], it means that the path is found
//4. Agreement: when map[i][j] is 0, it means the point has not passed through; when it is 1, it means the wall; 2 indicates that the passage can go; 3 means that the point has passed, but it can't go
//5. When walking through the maze, you need to determine a strategy (method): down - > right - > up - > left. If this point fails, go back
/**
*
* @param map Represent map
* @param i Where do you start
* @param j
* @return If the path is found, it returns true; otherwise, it returns false
*/
public static boolean setWay(int[][] map, int i, int j) {
if(map[6][5] == 2) { // Path found ok
return true;
} else {
if(map[i][j] == 0) { //If the current point has not passed
//According to the strategy, go down - > right - > up - > left
map[i][j] = 2; // It is assumed that this point is passable
if(setWay(map, i+1, j)) {//Go down
2.2 n queen problem
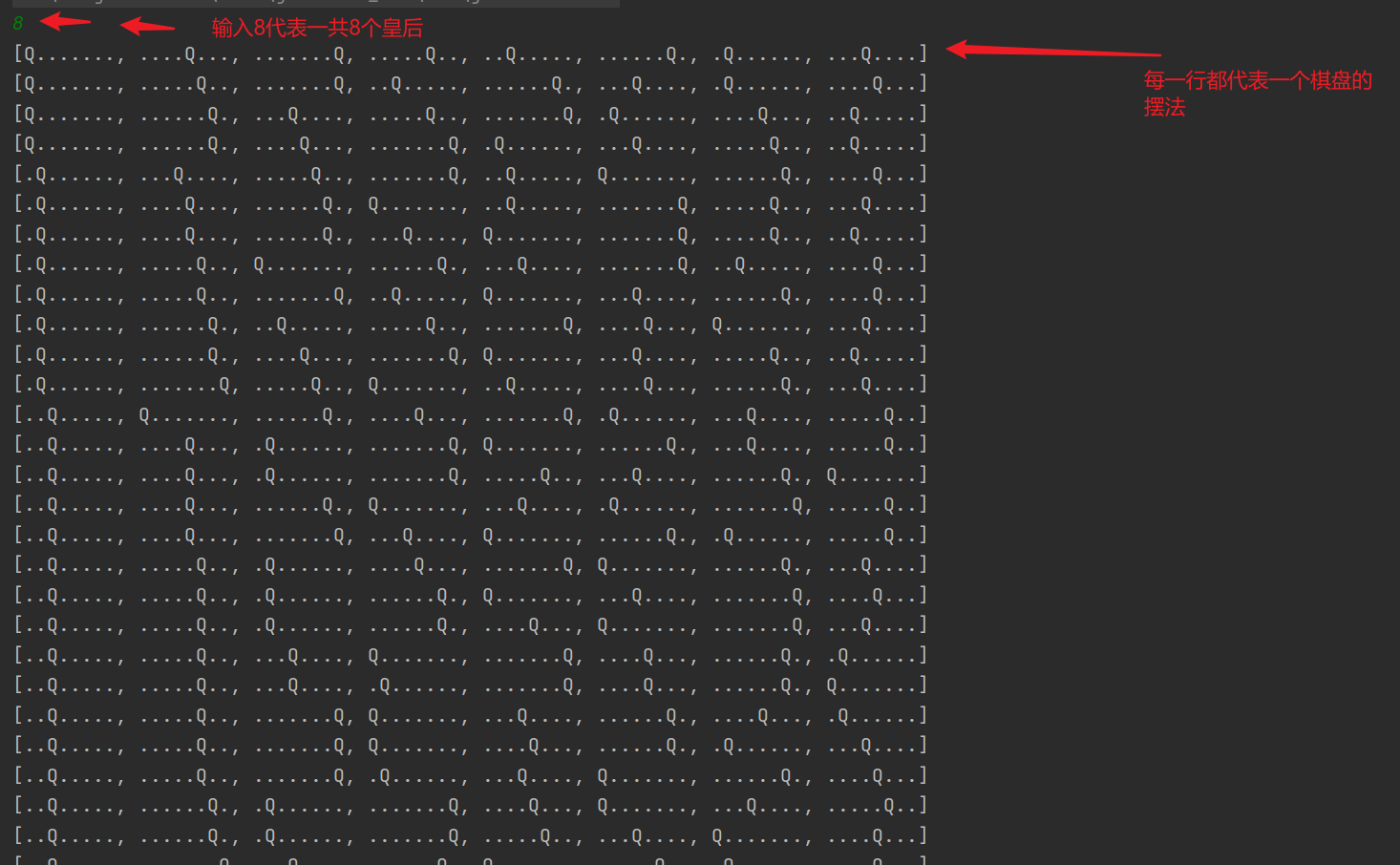
| Print all chessboard placement methods of the specified n queen, and store the results in the collection |
|---|
- Let's take queen 8 as an example (Queen 8 is 8 * 8 chessboard with 8 Queens, Queen n is n * n chess and cards with N Queens)

- Core ideas
- N stands for the number of queens. If there are n queens, it means how many rows and columns the chessboard has. If there are 8 Queens, it means 8 rows and 8 columns
- Abstract the Queen's position on the chessboard through a one-dimensional array, use the array subscript to represent the Queen's row, and use the subscript to correspond to the element value to represent the Queen's column. For example, when the subscript starts from 0. arr[0]=0 represents the first queen in the first row and column 1, and arr[4]=3 represents the current queen in the fifth row and column 4
- Judge whether the queen is in the same line, because we put it according to the line. Each queen can't be in the same line, so there is no need to consider the line
- To judge whether it is in the same column, we represent the column by the corresponding value of the array element, so we only need to judge whether the element values of the current queen and the existing queen are the same, so we can know whether there is a conflict. For example, a[0]=1 and a[3]=1, indicating that both the queen in the first row and the queen in the fourth row are in the first column, so there is a conflict
- Judge whether it is diagonal. According to mathematical knowledge, if the absolute value of abscissa subtraction of two coordinates is equal to the absolute value of ordinate subtraction, it means that two points form a diagonal, such as a[0]=0 and a[1]=1,|0-0| = 0 = |1-1|
- Operation effect
- code
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
private int arr[];//Used to store queens, where the subscript represents the row of each queen and the value represents the column of each queen
private ArrayList<List<String>> result = new ArrayList<>();
/**
* The entry method is used to receive how many queens there are
* @param n Number of queens
* @return
*/
public List<List<String>> solveQueues(int n){
arr = new int[n];
check(n,0);
return result;
}
/**
* Recursive method, pendulum queen method
* @param n The number of queens also represents the number of rows and columns, because 8 queens is a chessboard with 8 rows and 8 columns
* @param index Indicates the subscript of the array and the row (Queen) of the array
*/
public void check(int n,int index){
//Recursive exit condition. Because the array subscript starts from 0, when index==n, it is actually placing the n+1 Queen. At this time, you can exit
if(index==n){//If the exit conditions are met, it indicates that the checkerboard has been placed and processed. Here, the checkerboard result is encapsulated in the List set result
ArrayList<String> list = new ArrayList<>();
for(int i = 0;i < n;i++){
StringBuilder stringBuilder = new StringBuilder();
for(int j = 0;j < n;j++){
if(arr[i]==j){
stringBuilder.append("Q");
}else{
stringBuilder.append(".");
}
}
list.add(new String(stringBuilder));
}
result.add(list);
}else{
for(int i = 0;i < n;i++){//This loop represents the columns. For each row queen, try to put them on different columns. Because it is an n*n chessboard, n can represent both the number of rows and the number of columns
arr[index] = i;
if(judge(index)){//Judge whether the queen of the current row (index row) is placed in this column (column i). If there is no conflict, return true and place the next row
check(n,index+1);
}//If there is a conflict, put this line again
}
}
}
/**
* Judge whether the queen conflicts with the queen in front
* @param index Number of rows currently placed
* @return true Indicates that the current queen does not conflict with other queens, and false indicates conflict
*/
public boolean judge(int index){
for(int i = 0;i<index;i++){
//arr[i]==arr[index] because the elements of the array represent the column where the queen is located. If they are equal, it means that the two queens are in the same column
//For the two queens on the diagonal, abscissa subtraction (i-index) = = ordinate subtraction (arr[i]-arr[index]), but if the subtraction queen is on the right of the current queen, the subtraction will be negative. In order not to affect the judgment, use Math.abs() to take the absolute value
if(arr[i]==arr[index]||Math.abs(i-index)==Math.abs(arr[i]-arr[index])){//If the conditions are true, it means that the queen conflicts and can attack each other
return false;
}
}
return true;
}
/**
* Main function
* @param args
*/
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Main main = new Main();
while (sc.hasNext()) {//Used to accept multiple columns
int n = sc.nextInt();//Number of dynamic input queens
List<List<String>> lists;//Used to save the result set
lists=main.solveQueues(n);//Call the n Queen entry method
for(List<String> list1 : lists){//Traverse the output chessboard
System.out.println(list1);
}
}
sc.close();
}
}
3. Sorting

1. Insert sort
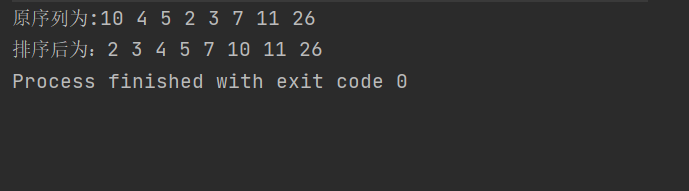
- It is to traverse the sequence elements to be sorted in turn, and insert each element into the appropriate position, that is, when traversing the first element, Ensure the order of this element (because an element is already orderly, so there is no need to arrange). When traversing the second element, ensure the order of the first two elements. When traversing the third element, ensure the order of the first three elements. The process of ensuring order is actually the process of inserting elements into appropriate positions, so it is called insertion sorting. (Note: each element is compared from the back to the front. This is a big problem, which we will talk about later)
Operation effect
code
public static void main(String[] args) {
int arr[] = {10,4,5,2,3,7,11,26};
System.out.println("The original sequence is:"+ Arrays.toString(arr));
//Insertion sorting is that subscripts 0 ~ 0 ensure order, 0 ~ 1 ensure order, 0 ~ 2 ensure order 0~i ensure order, and i is the number of elements to be sorted
//Insert sorting, 0 ~ 0 ordered, no row, directly row 0~i
for(int i = 1;i<=arr.length-1;i++){
for (int j = i-1;j >=0 && arr[j]>arr[j+1];j--){//Two by two, from small to large
arr[j] = arr[j]^arr[j+1];//Obtaining the XOR result is equivalent to a third variable and a key. The key XOR arr[i] will get arr[minIndex], and the XOR arr[minIndex] will get arr[i]
arr[j+1] = arr[j]^arr[j+1];//The XOR result is XOR arr[minIndex] again to get arr[i]
arr[j] = arr[j]^arr[j+1];//The XOR result is exclusive or arr[i] to get arr[minIndex]
}
}
System.out.print("After sorting:");
for(int i = 0;i<arr.length;i++){
System.out.print(arr[i]+" ");
}
}
2. Hill sort
- Disadvantages of insertion sorting
- Because each element of insertion sorting is compared from the back to the front, when the number of inserts is small, the number of sorting (comparison) times increases significantly. For example, when 10000 numbers are sorted, the last number is the smallest, so the last number alone needs to be compared 9999 times to complete the sorting of the last number, which will be very inefficient
- Shell Sort
- Hill and 1959 proposed an improved version of insertion sorting, which is more efficient and can reduce incremental sorting
- The idea of division and rule is to divide and rule, Basically, it is grouped according to a certain increment of the subscript (for example, if the increment is 5, then the elements with subscript 0 and those with subscript 0 + 5 = 5 are grouped. If there are elements with subscript 5 + 5 = 10, then 0, 5, 10. The three subscript elements are divided into a group, and so on). Insert sorting is used for each group, and then the increment will be less and less. When the increment is 1, the whole file will just become a group. Finally, insert sorting is performed again Complete the overall sorting (increment reduction rule, increment = increment / 2, the initial increment is the sequence length, the second is the increment result calculated by the initial increment, and the third is the increment result calculated by the second)
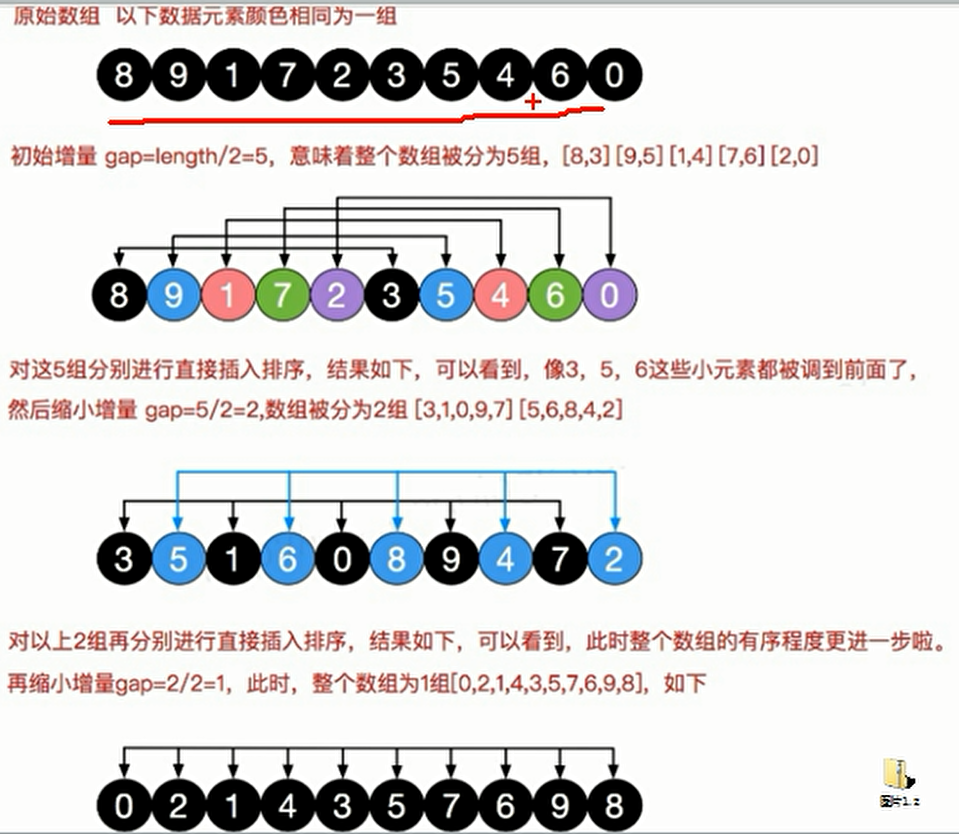

| There are two implementation methods of Hill sort. The exchange method realizes Hill sort. The idea is simple, but the speed is very slow. The mobile method realizes Hill sort. The idea is not easy to understand, but the speed is fast |
|---|
- The move method is to eliminate useless exchange operations, such as 4, 5, 3 and 1. To insert and sort 1, we first save the number 1, then move 3 to the position of 1, 5 to the position of 3, 4 to the position of 5, and finally store 1 to the position of 4. In this way, the exchange operation is eliminated and the efficiency is greatly improved
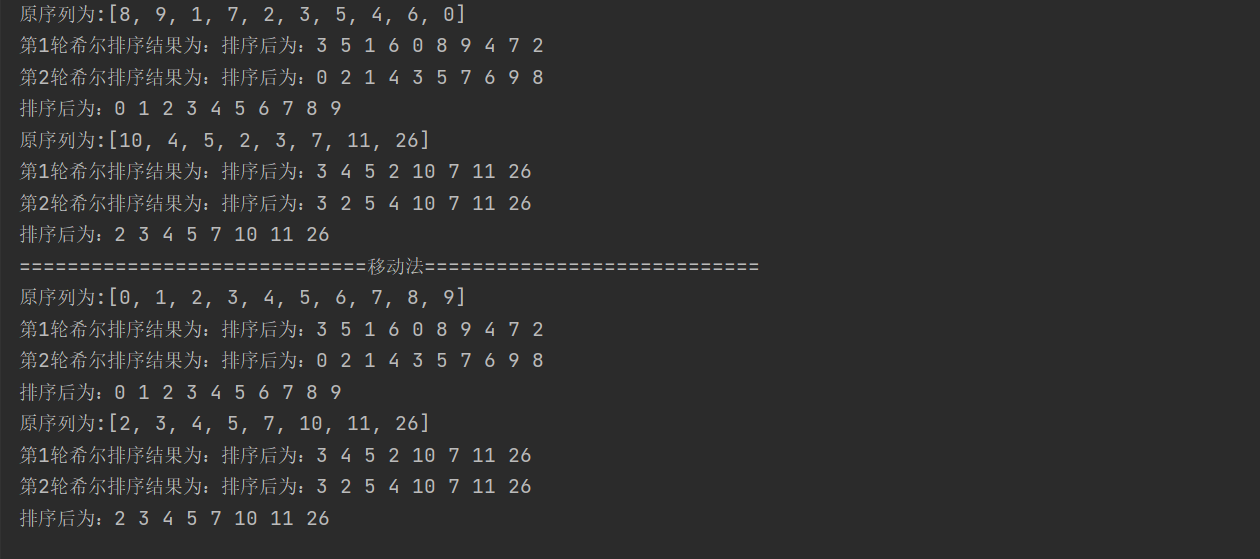
- 80000 groups of data were tested and found (on the premise of not using bit operation), 80000 data were sorted using insert sorting, which took 4 seconds, Hill sorting using exchange method took 14 seconds, and Hill sorting using mobile method took 4 milliseconds (1 second = 1000 milliseconds) (the following figure shows the consumption time of using bit operation)

- Operation results
- code
import java.util.Arrays;
import java.util.Date;
import java.util.Random;
public class Test {
public static void main(String[] args) {
int arr[]= {8,9,1,7,2,3,5,4,6,0};
int arr1[]={10,4,5,2,3,7,11,26};
System.out.println("The original sequence is:"+ Arrays.toString(arr));
shellSort1(arr);
print(arr);
System.out.println("The original sequence is:"+ Arrays.toString(arr1));
shellSort1(arr1);
print(arr1);
System.out.println("=============================Moving method============================");
int arr2[]= {8,9,1,7,2,3,5,4,6,0};
int arr3[]={10,4,5,2,3,7,11,26};
System.out.println("The original sequence is:"+ Arrays.toString(arr));
shellSort2(arr2);
print(arr2);
System.out.println("The original sequence is:"+ Arrays.toString(arr1));
shellSort2(arr3);
print(arr3);
//If you want to test, you need to comment out the output statements in Hill sorting method
// System. out. Println ("=================================================================================;
// int array[] = new int[80000];
// For (int i = 0; I < 80000; I + +) {/ / generate 80000 [0800000] random numbers
// array[i] = (int) (Math.random()*800000);
// }
// int[] array2 = array.clone();
// int[] array3 = array.clone();
// long start = new Date().getTime();
// insertSort(array);
// long end = new Date().getTime();
// System.out.println("insert sort consumption time" + (end start));
// start = new Date().getTime();
// shellSort1(array);
// end = new Date().getTime();
// System.out.println("exchange Fisher sort consumption time" + (end start));
// start = new Date().getTime();
// shellSort2(array);
// end = new Date().getTime();
// System.out.println("mobile Fisher sort consumption time" + (end start));
}
/**
* Insert sort
*/
public static void insertSort(int arr[]){
//Insert sorting, 0 ~ 0 ordered, no row, directly row 0~i
for(int i = 1;i<=arr.length-1;i++){
for (int j = i-1;j >=0 && arr[j]>arr[j+1];j--){//Two by two, from small to large
arr[j] = arr[j]^arr[j+1];//Obtaining the XOR result is equivalent to a third variable and a key. The key XOR arr[i] will get arr[minIndex], and the XOR arr[minIndex] will get arr[i]
arr[j+1] = arr[j]^arr[j+1];//The XOR result is XOR arr[minIndex] again to get arr[i]
arr[j] = arr[j]^arr[j+1];//The XOR result is exclusive or arr[i] to get arr[minIndex]
}
}
}
/**
* Print
*/
public static void print(int arr[]){
System.out.print("After sorting:");
for(int i = 0;i<arr.length;i++){
System.out.print(arr[i]+" ");
}
System.out.println();
}
/**
* Swap Fasher sort
* @param arr array
*/
public static void shellSort1(int arr[]){
int gap = arr.length/2;//increment
int index = 1;//Code that can be omitted for printing
while(gap>1){//If the increment is 1, only the last insertion sort is required
for(int i = gap;i < arr.length;i++){//Control grouping, but insert sorting, always, the latter constantly compares the former
for(int j = i-gap;j >= 0 && arr[j] > arr[j+gap];j-=gap){//Control incremental sorting, and compare from small to large, from back to front
arr[j]=arr[j]^arr[j+gap];
arr[j+gap] = arr[j]^arr[j+gap];
arr[j] = arr[j]^arr[j+gap];
}
}
gap /= 2;
System.out.print("The first"+index+"The sorting result is:");//Omitted code for printing
index++;
print(arr);
}
insertSort(arr);
}
/**
* Mobile Fasher sort
* @param arr array
*/
public static void shellSort2(int arr[]){
int gap = arr.length/2;//increment
int index = 1;//Code that can be omitted for printing
while(gap>1){//If the increment is 1, only the last insertion sort is required
for(int i = gap;i < arr.length;i++){//Control grouping, but insert sorting, always, the latter constantly compares the former
//
if(arr[i-gap] > arr[i]){//If you need to exchange positions, record the current value
int temp = arr[i];//Record the current value to be exchanged, and move the other numbers in front of it back in turn
int j ;
for(j = i -gap;j >= 0 && temp < arr[j];j-=gap){
arr[j+gap] = arr[j];//Element forward
}
arr[j+gap] = temp;
}
}
gap /= 2;
System.out.print("The first"+index+"The sorting result is:");
index++;
print(arr);
}
insertSort(arr);
}
}
3. Quick sort
- Quick sort is an improved version of bubble sort. The divide and conquer idea is still adopted. First, the data is divided into two parts through one-time sorting. All the data in one part is smaller than all the data in the other part, and then the two parts of data are sorted quickly according to this method. The whole process can be realized by recursion.
- Just get a set of data and find a number first, As the middle number (you can directly take the number in the middle of the sequence, or take the last number, or the first number). Then, according to this number, you can first arrange into two groups. There is no order, that is, those larger than the middle number are divided into one group, and those smaller than the middle number are divided into one group. Whichever group the middle number belongs to at last is optional. Then, you can quickly sort the two groups respectively (like bubbling, pop the middle number out each time)
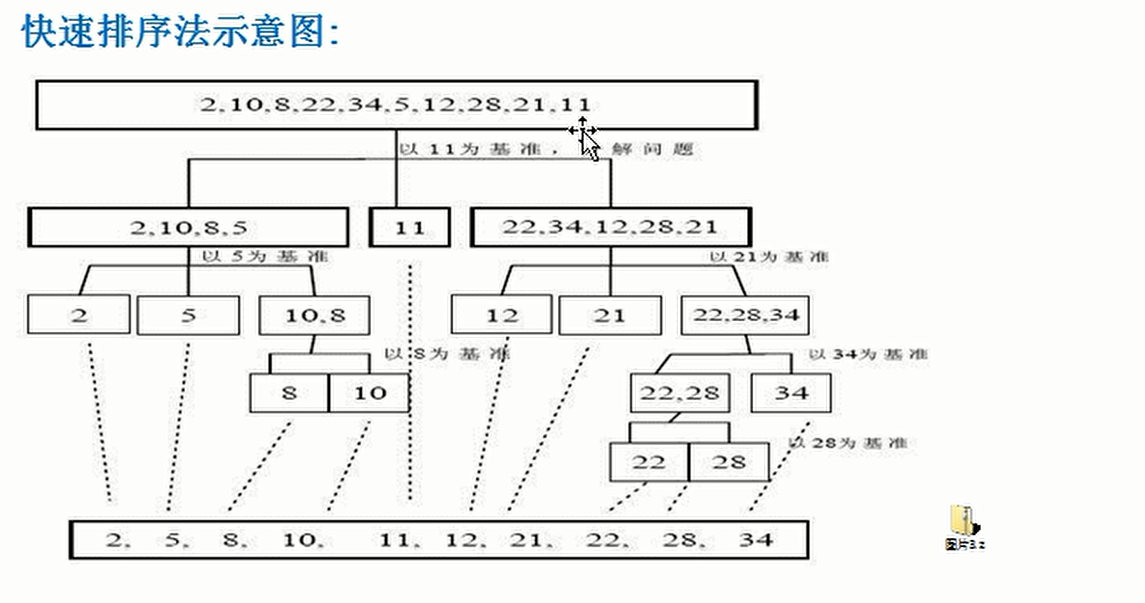
- Realization idea and operation effect
- first, We choose the middle number (benchmark number). Here, we specify that the first number of the sequence is the benchmark number and save the benchmark number. Then create two subscripts, which are located on the leftmost and rightmost sides of the sequence. Find the value greater than the middle number from the right and put it on the left. Find the value less than the middle number on the left and put it on the right. Finally, the last position of the left subscript is the middle, and put the middle number in Just go
- code
import java.util.Arrays;
import java.util.Date;
public class Test {
public static void main(String[] args) {
int arr[]= {8,9,1,7,2,3,5,4,6,0};
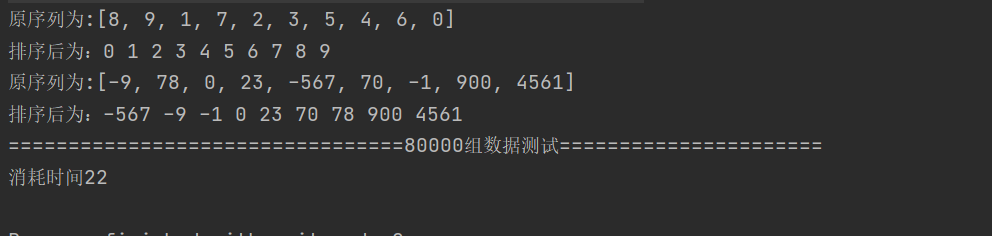
int arr1[]={-9,78,0,23,-567,70, -1,900, 4561};
System.out.println("The original sequence is:"+ Arrays.toString(arr));
quickSort(arr,0,arr.length-1);
print(arr);
System.out.println("The original sequence is:"+ Arrays.toString(arr1));
quickSort(arr1,0,arr1.length-1);
print(arr1);
System.out.println("=================================80000 Group data test======================");
int array[] = new int[80000];
for (int i = 0 ;i<80000;i++){//Generate 80000 random numbers [08000000]
array[i] = (int) (Math.random()*800000);
}
long start = new Date().getTime();
quickSort(array,0,array.length-1);
long end = new Date().getTime();
System.out.println("Time consuming"+(end-start));
}
/**
* Quick sort
*/
public static void quickSort(int[] a, int left, int right) {
if (left < right) {//If l > R indicates that it has been arranged, it can be recursive
int l = left;//Left subscript
int r = right;//Right subscript
int temp = a[l];//Save an indicator variable
while (l < r) {//If l > = R, exit the cycle, indicating that the discharge is complete
while(l < r && a[r] > temp)//Traverse from right to left to find a number less than temp, but cannot exceed l
r--; // Find the first number less than temp from right to left
if(l < r)//If the above cycle ends and still l < R, it means that the exchange conditions are met
a[l++] = a[r];//Put the first number on the right that is less than temp on the left, because the above temp saves the value, so you don't have to worry about overwriting. Equivalent to a [l] = a [R]; l++; Short form of two statements,
while(l < r && a[l] < temp)//Traverse from left to right to find a number greater than temp, but cannot exceed r
l++; // Find the first number greater than temp from left to right
if(l < r)//If the above cycle ends and still r > L, it means that the exchange conditions are met
a[r--] = a[l]; //Put the first number on the left that is greater than temp on the right, because its value has been moved to the left. Don't worry about overwriting
}
a[l] = temp;//The location of the last l subscript is the location that temp can finally determine
quickSort(a, left, l-1); /* Recursive call */
quickSort(a, l+1,right); /* Recursive call */
}
}
/**
* Print
*/
public static void print(int arr[]){
System.out.print("After sorting:");
for(int i = 0;i<arr.length;i++){
System.out.print(arr[i]+" ");
}
System.out.println();
}
}
4. Merge and sort
- Using the sorting method realized by the merging idea and the classical divide and conquer strategy, the problem is divided into several small problems, solved in turn, and finally the results of small problems are repaired together. That is, divide and rule
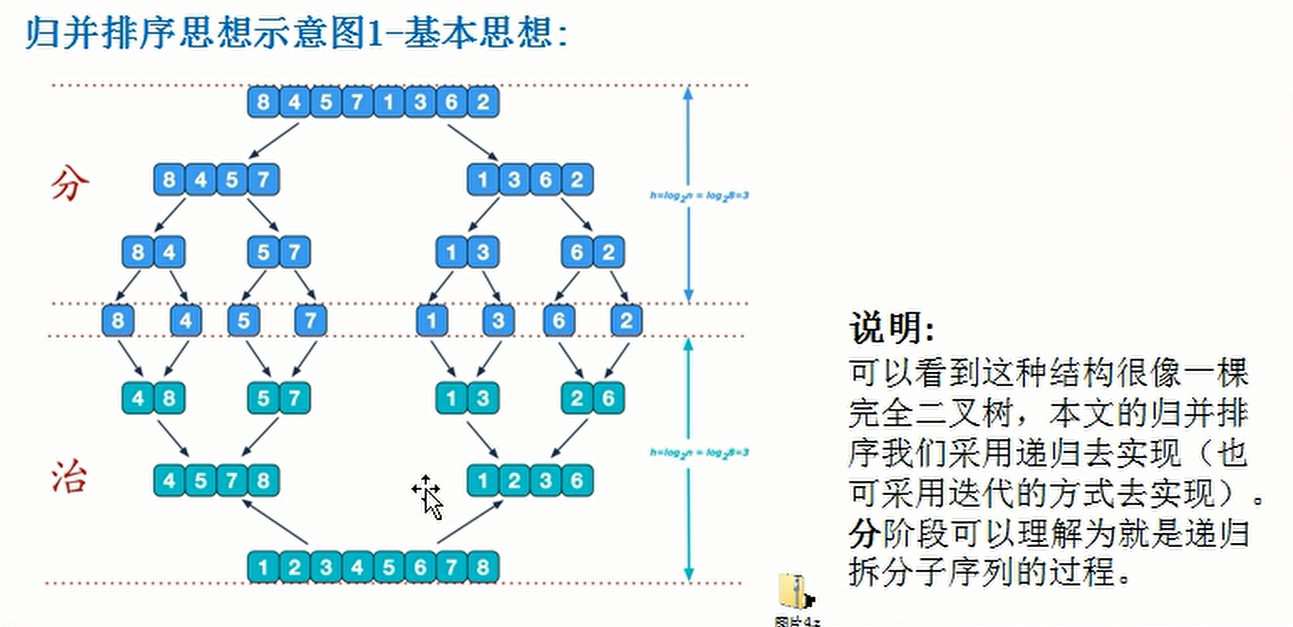
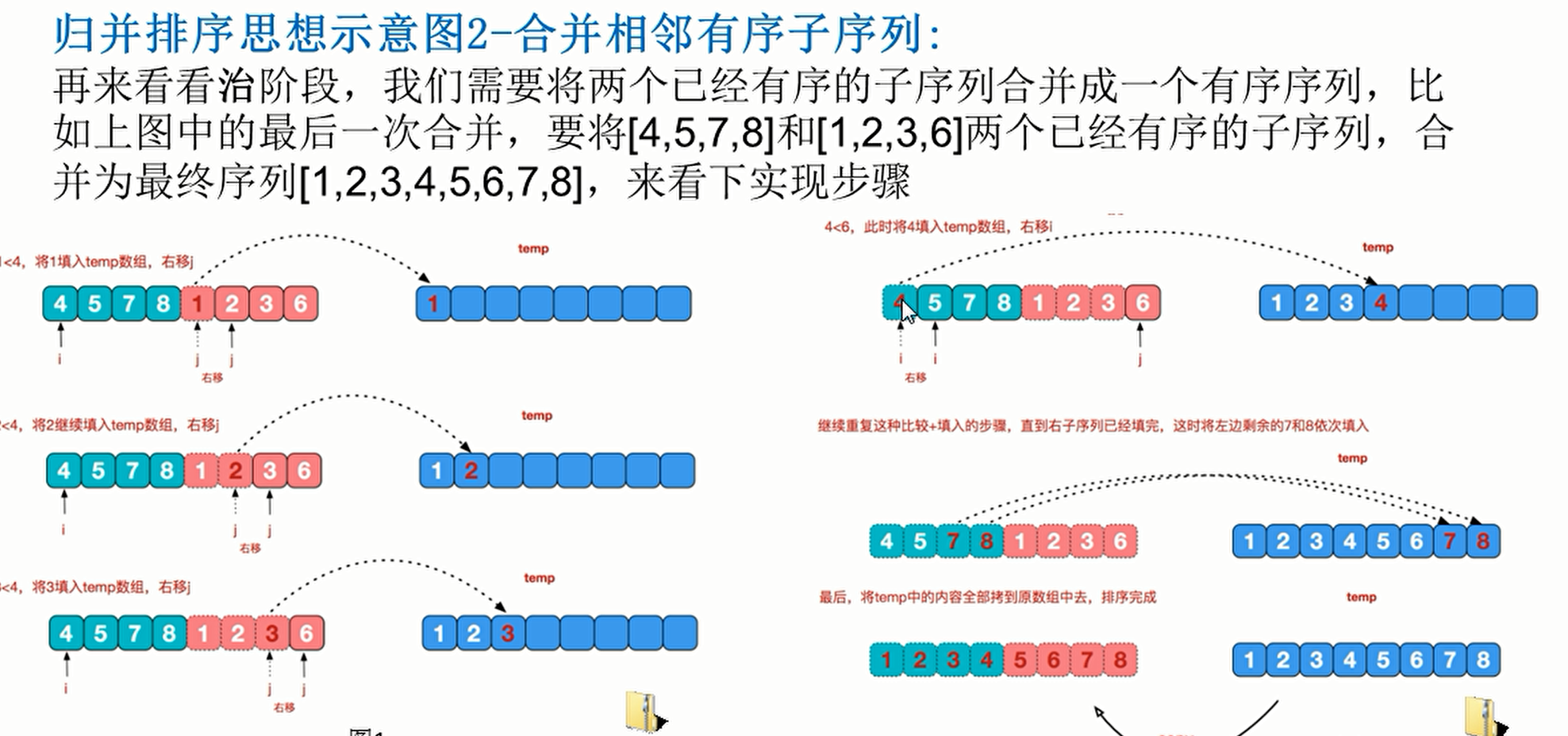
- Operation effect

- code
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int arr[] = {8,4,5,7,1,3,6,2};
int temp[] = new int[arr.length];
System.out.println("The original array is:"+Arrays.toString(arr));
mergeSort(arr,0,arr.length-1,temp);
System.out.println("After sorting:"+Arrays.toString(arr));
}
//Opening + closing method
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if(left < right) {
int mid = (left + right) / 2; //Intermediate index
//Decompose recursively to the left
mergeSort(arr, left, mid, temp);
//Decompose recursively to the right
mergeSort(arr, mid + 1, right, temp);
//merge
merge(arr, left, mid, right, temp);
}
}
/**
* Method of merging final results
* @param arr Array to sort
* @param left Left ordered sequence, initial index
* @param mid Intermediate index
* @param right Right index
* @param temp Transfer array to help merge
*/
public static void merge(int arr[],int left,int mid,int right,int[] temp){
int i = left;//Initialization i, the initial index of the left ordered sequence
int j = mid + 1;//Initialization j, the initial index of the ordered sequence on the right
int t = 0;//Points to the current index of the temp array
//1. First, fill the left and right (ordered) data into the temp array according to the rules
//Until one side of the ordered sequence on the left and right is processed
while(i <= mid && j <= right){//
//If the current element of the left ordered sequence is less than or equal to the current element of the right ordered sequence
//Then copy the current element on the left to the temp array. After filling, remember to move the subscript
if(arr[i] <= arr[j]){
temp[t] = arr[i];
t += 1;
i += 1;
}else{//If the current element on the right is smaller than the current element on the left, fill it into the temp array
temp[t] = arr[j];
t += 1;
j += 1;
}
}
//2. Fill all the data on the side with remaining data into temp in turn
while(i <= mid){//The ordered sequence on the left and the remaining elements are filled into temp
temp[t] = arr[i];
i++;
t++;
}
while(j <= right){//The ordered sequence on the right and the remaining elements are filled into temp
temp[t] = arr[j];
j++;
t++;
}
//3. Copy the elements of the temp array to arr, but not all of them are copied every time
t = 0;
int tempLeft = left;
while(tempLeft <= right){
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
}
5. Cardinality sorting (bucket sorting)
- It belongs to sorting during allocation, also known as bucket method. As the name suggests, it allocates the elements to be sorted to some buckets through the values of each bit of the key value
- Cardinality sorting method is a stable sorting method with high efficiency
- Bucket sort extension
- It was invented by Herman Holley in 1887. Cut the integer into different numbers according to the number of digits, and then compare them respectively according to each number of digits
- basic thought
- Unify all values to be compared into the same digit length, and fill zero in front of the shorter digit. Then start from the low order and sort once in turn. In this way, the sequence will be ordered from the lowest order to the highest order

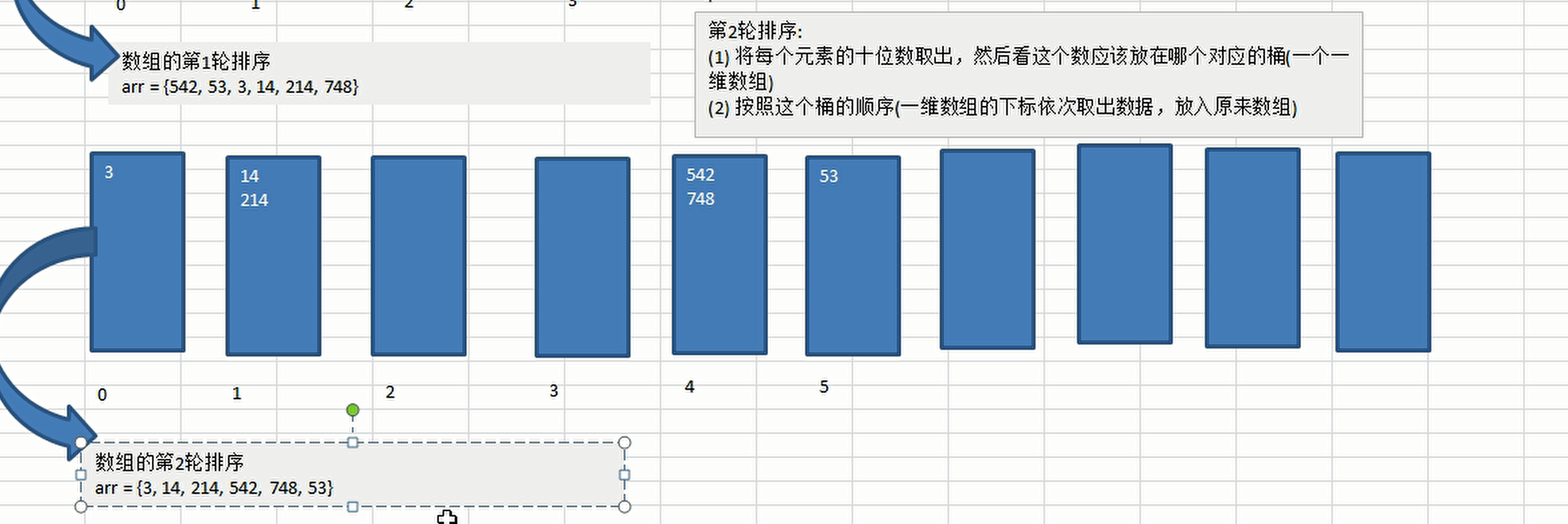
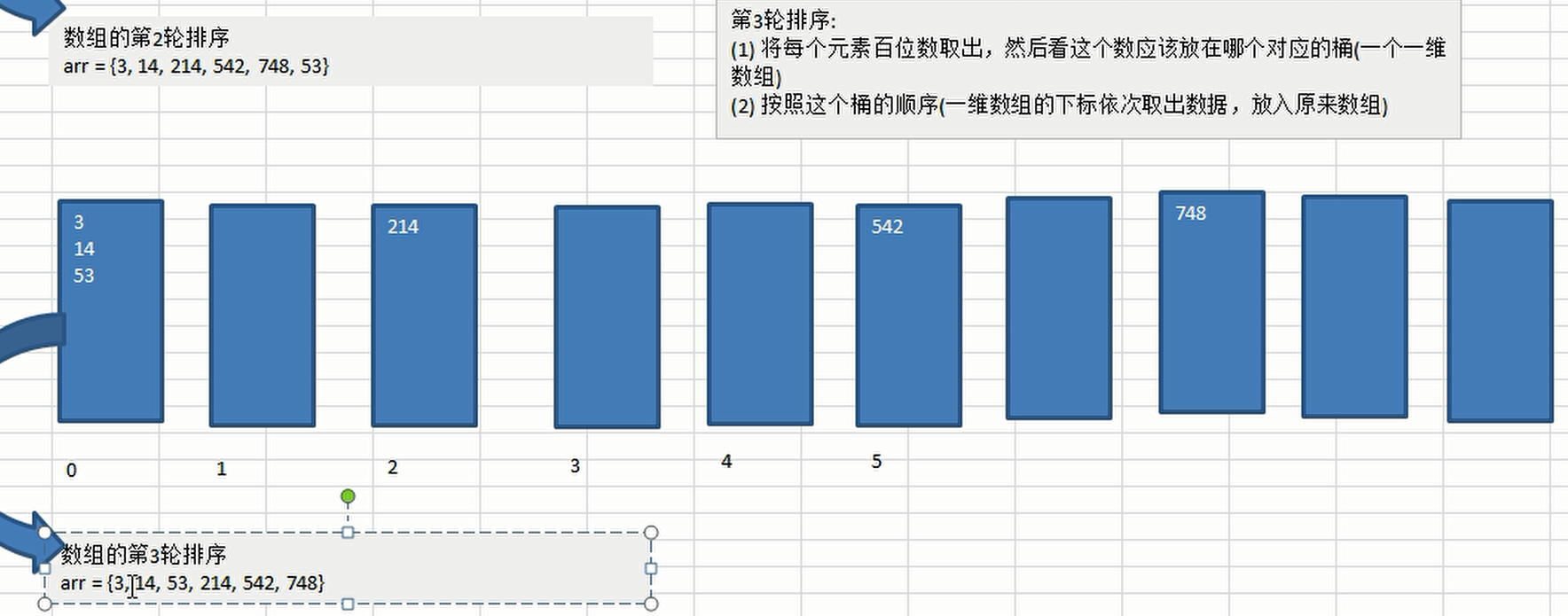
- Realization idea
- First, determine the maximum number of bits of the array data. For example, if the maximum number is 1900, the maximum number of bits is 4
- Creating 10 buckets is a two-dimensional array with 10 one-dimensional arrays. Each one-dimensional array represents a bucket, representing 0-9 respectively
- Creating valid data records for buckets is a one-dimensional array that records the number of valid data for each bucket
- Traverse according to the maximum number of bits. If you want to sort from small to large, you need to compare the bits first, put them into the corresponding bucket according to the number of bits, and then let the bucket effective data record increase automatically
- Then traverse the bucket in turn, put the data in the bucket into the original array, then clear the bucket effective data record, then compare ten bits, and so on
- Operation effect
- Code (no negative number processing)
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int arr[] = {53,3,542,748,14,214};
radixSort(arr);
int arr1[] = {9,7,13,0,5,0,14,21,197};
radixSort(arr1);
}
/**
* Cardinality sort
* @param arr Array to sort
*/
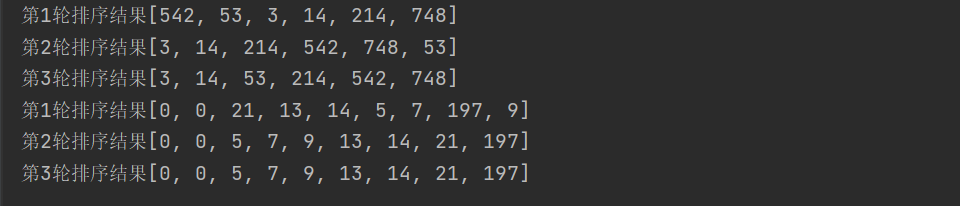
public static void radixSort(int arr[]){
//1. Through Java stream API arrays stream(arr). max(). Getasint() gets the maximum number of arrays, then + "" turns it into a string, and obtains the string length through the length() method to determine the maximum number of bits
int maxLength = (Arrays.stream(arr).max().getAsInt()+"").length();
//2. Create buckets. There are 10 buckets in total. The length of each bucket is set to arr.length because the number of data is uncertain, so there will be no overflow. Typical space changes time
int bucket[][] = new int[10][arr.length];
//3. Create a valid data record of the bucket, record the number of valid elements of each bucket, and the subscript
int bucketEleCount[] = new int[10];
//4. Traverse according to the maximum number of digits, and rank from small to large
for(int i = 0;i < maxLength;i++){
//Traversal array into bucket
for( int j = 0;j<arr.length;j++){
// Take out the corresponding digit (int) math Pow (10, I) represents the i-th power of 10
int num = arr[j] / (int)Math.pow(10,i) % 10;//1983, for example, I = 01983 / 1 = 1983% 10 = 3, I = 11983 / 10 = 198% 10 = 8
// Put in the corresponding bucket. For example, if num = 1, put the bucket with subscript 1 in the first position, which is determined by the subscript of bucketEleCount[num] record
bucket[num][bucketEleCount[num]] = arr[j];
bucketEleCount[num]++;//After playing, move the subscript back
}
//5. Put the data in the bucket into the original array in turn
int index = 0;//Represents the subscript of the original array
for(int j = 0;j<bucketEleCount.length;j++){//You can traverse the bucket directly by traversing the subscripts, which are saved in the bucketEleCount array
if(bucketEleCount[j]!=0){//If there is a value in the bucket, traverse again
for(int z = 0;z < bucketEleCount[j];z++){
arr[index++] = bucket[j][z];
}
}
//Reset bucket subscript
bucketEleCount[j]=0;
}
System.out.println("The first"+(i+1)+"Round sort result"+Arrays.toString(arr));
}
}
}
6. Heap sorting
- Heap sorting is a sort algorithm designed by using heap (data structure). It belongs to selective sorting. The worst and best, the average time complexity is O(n logn), and it is unstable sorting
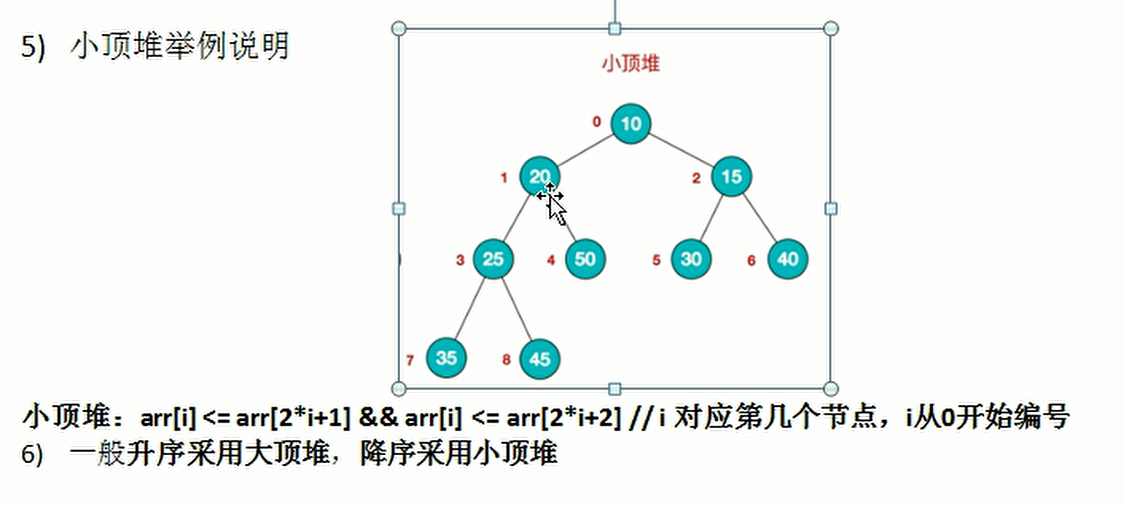
- Heap is a complete binary tree with the following properties:
- The value of each node is greater than or equal to the value of its left and right child nodes, which is called large top heap,
- There is no size relationship between the value of the left child and the value of the right child of the node.
- The value of each node is less than or equal to the value of its left and right child nodes, which is called small top heap

| Basic idea of heap sorting (taking the use of large top heap in ascending order as an example) |
|---|
- The sequences to be sorted form a large top heap
- Because the maximum value of the large top heap is the root node, it is exchanged with the end element, and the end value is the maximum value
- Then, the remaining n-1 elements form a large top heap, and repeat the above operations. Each construction can obtain a maximum value, and finally get an ordered sequence
- Formula used (basic formula of binary tree)
- arr[i] < = arr [2I + 1] & & arr[i] < = arr [2I + 2] small top heap condition, the current non leaf node arr[i], left node and right node are smaller than it, and the large top heap is just the opposite, both left and right are larger than itself
- First non leaf node arr.length/2-1
- The left child node of the current node, i2+1, and the right child node of the current node, i2+2
- Basic implementation ideas
- Build a large top heap from below the binary tree
- Each time, the top elements of the heap are exchanged to the back of the heap, so that the whole array is formed in turn. The last one is the maximum value, and the penultimate one is the penultimate value
- Then remove the rows behind the array, build the heap again, exchange, and so on
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int arr[] = {4,6,8,5,9};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
/**
* Heap sort
* @param arr array
*/
public static void heapSort(int arr[]){
//For the first time to build a large top pile, you need to do it alone. The later ones should follow the rules in turn. Of course, there are other methods
//1. Build the sequence into a large top heap. length/2-1 is the first non leaf node, length/2-2 is the second non leaf node, and so on. 0 is the root node of the whole sequence
for(int i = arr.length /2 -1;i >= 0 ;i--){
//I is each non leaf node. Build it from bottom to top, call the adjustHeap method, let the node i points to as the root, and save the maximum value
adjustHeap(arr,i,arr.length);
}
//2. Build a large top heap above, obtain a maximum value, then exchange, and then build the remaining large top heap to make the remaining maximum values orderly
for(int i = arr.length-1;i>0;i--){
// 2.1 the top element is exchanged with the end element. At this time, the maximum value is saved to the end, and the length needs to be reduced
arr[i]=arr[i]^arr[0];
arr[0]=arr[i]^arr[0];
arr[i]=arr[i]^arr[0];
// 2.2 readjust the structure (build the remaining large top heap) to meet the heap definition, and then continue to exchange until the whole sequence is in order
adjustHeap(arr,0,i);//It starts at 0 every time, but the length decreases every time, because the last element is in order
}
}
/**
* To build a large top heap with the element specified by the i subscript as the root node (parent node) is to consider only the i node itself and all its descendants, not other nodes of the array
* @param arr array
* @param i The non leaf node is indexed in the array and used as the root to build the large top heap
* @param length Adjust the number of elements and gradually reduce it, because there is a maximum value each time, and there is no need to build it again
*/
public static void adjustHeap(int arr[],int i ,int length){
int temp = arr[i];//Saves the value of the current non leaf node
//Build a large top heap with i as the root (parent node). i*2+1 is the subscript of the left child node of the current i node, and K*2+1 is the subscript of the left child node of k node
for(int k = i*2+1;k<length;k=k*2+1){
if(k+1 < length && arr[k] < arr[k+1]){//If the right node is larger than the left node, the right node is directly considered. k is the subscript of the left node and + 1 is the subscript of the right node
k++;
}
//At this time, k is the larger one of the left and right nodes of node I. if it is larger than node i, its value is given to node I
if(arr[k]>temp){
arr[i] = arr[k];
i = k;//Here i points to its child node k, and the next loop is its child node
}else{
break;//If it is smaller than i, you can exit the loop without exchanging values
}
}
//At this time, the construction of the large top heap is completed, and i is the maximum value of the tree of the parent node, which is placed at the top
arr[i] = temp;//Finally, assign the value of temp to the location where the replacement is made
}
}
4. Find
- Common searches in java include sequential (linear) search, binary / half search, interpolation search and Fibonacci search
1. Binary search (recursive)
- The premise of binary search is that the sequence is orderly
- First, we need to find a number. First, we need to find the number in the middle of the sequence and compare it. If it is larger than the middle number, we will continue to find it on the right. If it is smaller than the middle number, we will find it on the left
- For example, if it is larger than the middle number, go to the right. At this time, you need to find the middle number of the right half of the sequence again, and then continue to judge, and so on
- Operation effect

- code
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
//Note: the premise of binary search is that the array is ordered
public class Test {
public static void main(String[] args) {
int arr[] = { 1, 8, 10, 89,1000,1000, 1234 };
int arr1[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 , 11, 12, 13,14,15,16,17,18,19,20 };
//
System.out.println("The sequence is:"+ Arrays.toString(arr1));
int resIndex = binarySearch(arr1, 0, arr1.length - 1, 8);
System.out.println("The subscript of element 8 is resIndex=" + resIndex);
System.out.println("The sequence is:"+Arrays.toString(arr));
List<Integer> resIndexList = binarySearch2(arr, 0, arr.length - 1, 1000);
System.out.println("The subscript of element 1000 is resIndexList=" + resIndexList);
}
// Binary search algorithm
/**
*
* @param arr
* array
* @param left
* Index on the left
* @param right
* Index on the right
* @param findVal
* Value to find
* @return If it is found, it returns the subscript. If it is not found, it returns - 1
*/
public static int binarySearch(int[] arr, int left, int right, int findVal) {
// When left > right, it means that the whole array is recursive, but it is not found
if (left > right) {
return -1;
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (findVal > midVal) { // Recursive right
return binarySearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // Left recursion
return binarySearch(arr, left, mid - 1, findVal);
} else {
return mid;
}
}
//Complete an after class thinking question:
/*
* After class thinking questions: {1,8, 10, 89, 1000, 10001234} when in an ordered array,
* How to find all values when there are multiple identical values, such as 1000 here
*
* Train of thought analysis
* 1. Do not return the mid index value immediately after it is found
* 2. Scan to the left of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
* 3. Scan to the right of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
* 4. Return Arraylist to
*/
public static List<Integer> binarySearch2(int[] arr, int left, int right, int findVal) {
System.out.println("hello~");
// When left > right, it means that the whole array is recursive, but it is not found
if (left > right) {
return new ArrayList<Integer>();
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (findVal > midVal) { // Recursive right
return binarySearch2(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // Left recursion
return binarySearch2(arr, left, mid - 1, findVal);
} else {
// *Train of thought analysis
// * 1. Do not return the mid index value immediately after it is found
// * 2. Scan to the left of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
// * 3. Scan to the right of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
// * 4. Return Arraylist to
List<Integer> resIndexlist = new ArrayList<Integer>();
//Scan to the left of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
int temp = mid - 1;
while(true) {
if (temp < 0 || arr[temp] != findVal) {//sign out
break;
}
//Otherwise, put temp into reindexlist
resIndexlist.add(temp);
temp -= 1; //temp shift left
}
resIndexlist.add(mid); //
//Scan to the right of the mid index value and add the subscripts of all elements satisfying 1000 to the set ArrayList
temp = mid + 1;
while(true) {
if (temp > arr.length - 1 || arr[temp] != findVal) {//sign out
break;
}
//Otherwise, put temp into reindexlist
resIndexlist.add(temp);
temp += 1; //temp shift right
}
return resIndexlist;
}
}
}
2. Interpolation search
- The improved version of binary search is because if we want to find the first element of an ordered sequence, it needs to be halved from the middle one at a time, but it takes a lot of time. Unlike binary search, interpolation search starts from the adaptive mid each time
- The binary search formula is mid = (left+right)/2, while the interpolation search formula is mid = left + (key - a [left]) / (a [right] - a [left]) * (high low)

- Code (like binary search, change a formula, and then exit the recursion. Just change the conditions)
//Write interpolation search algorithm
//Interpolation search algorithm also requires that the array is ordered
/**
*
* @param arr array
* @param left Left index
* @param right Right index
* @param findVal Find value
* @return If it is found, the corresponding subscript is returned. If it is not found, it returns - 1
*/
public static int insertValueSearch(int[] arr, int left, int right, int findVal) {
System.out.println("Interpolation lookup times~~");
//Note: findval < arr [0] and findval > arr [arr.length - 1] must be required
//Otherwise, the mid we get may cross the border
if (left > right || findVal < arr[0] || findVal > arr[arr.length - 1]) {
return -1;
}
// Find the mid, adaptive
int mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);
int midVal = arr[mid];
if (findVal > midVal) { // Description should recurse to the right
return insertValueSearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // Description left recursive lookup
return insertValueSearch(arr, left, mid - 1, findVal);
} else {
return mid;
}
}
3. Fibonacci search
- Use the Fibonacci sequence to find. When searching, you need to first determine the maximum subscript of the array. If it is smaller than the corresponding Fibonacci sequence, you need to create a new array to fill the data and cooperate with the Fibonacci sequence
- In fact, search is to search in the new array, constantly through the Fibonacci sequence
- The core idea is how to cooperate with Fibonacci, so there is no need to explain too much, just look at the code understanding
import java.util.Arrays;
public class FibonacciSearch {
public static int maxSize = 20;
public static void main(String[] args) {
int [] arr = {1,8, 10, 89, 1000, 1234};
System.out.println("index=" + fibSearch(arr, 189));// 0
}
//Since we need to use Fibonacci sequence after mid=low+F(k-1)-1, we need to obtain a Fibonacci sequence first
//A Fibonacci sequence is obtained by non recursive method
public static int[] fib() {
int[] f = new int[maxSize];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < maxSize; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
//Write Fibonacci search algorithm
//Write the algorithm in a non recursive way
/**
*
* @param a array
* @param key Key (value) we need to find
* @return Returns the corresponding subscript, if not - 1
*/
public static int fibSearch(int[] a, int key) {
int low = 0;
int high = a.length - 1;
int k = 0; //Subscript representing the Fibonacci division value
int mid = 0; //Store mid value
int f[] = fib(); //Get Fibonacci sequence
//Get the subscript of Fibonacci division value
while(high > f[k] - 1) {
k++;
}
//Because the f[k] value may be greater than the length of a, we need to use the Arrays class to construct a new array and point to temp []
//The insufficient part will be filled with 0
int[] temp = Arrays.copyOf(a, f[k]);
//In fact, you need to fill temp with the last number of the a array
//give an example:
//temp = {1,8, 10, 89, 1000, 1234, 0, 0} => {1,8, 10, 89, 1000, 1234, 1234, 1234,}
for(int i = high + 1; i < temp.length; i++) {
temp[i] = a[high];
}
// Use while to cycle and find our number key
while (low <= high) { // As long as this condition is met, you can find it
mid = low + f[k - 1] - 1;
if(key < temp[mid]) { //We should continue to look in front of the array (left)
high = mid - 1;
//Why k--
//explain
//1. All elements = front elements + rear elements
//2. f[k] = f[k-1] + f[k-2]
//Because there are f[k-1] elements in front, you can continue to split f[k-1] = f[k-2] + f[k-3]
//That is, continue to find K in front of f[k-1]--
//That is, the next cycle mid = f[k-1-1]-1
k--;
} else if ( key > temp[mid]) { // We should continue to look behind the array (to the right)
low = mid + 1;
//Why k -=2
//explain
//1. All elements = front elements + rear elements
//2. f[k] = f[k-1] + f[k-2]
//3. Since we have f[k-2], we can continue to split f[k-1] = f[k-3] + f[k-4]
//4. Find k -=2 in front of f[k-2]
//5. That is, the next cycle mid = f[k - 1 - 2] - 1
k -= 2;
} else { //find
//You need to determine which subscript is returned
if(mid <= high) {
return mid;
} else {
return high;
}
}
}
return -1;
}
}
4. Binary search (non recursive version)
- Operation effect

- code
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int[] arr = {1,3,8,10,11,67,100};
System.out.println("The array elements are:"+Arrays.toString(arr));
int index = binarySearch(arr,10);
System.out.println("Find element 10 with subscript"+index);
}
/**
* Binary search non recursive version
* @param arr Array to be found
* @param target Number of to find
* @return Return the corresponding subscript, - 1 is not found
*/
public static int binarySearch(int[] arr,int target){
int left = 0;//Left subscript, starting at 0
int right = arr.length - 1; //Right subscript, starting with the subscript of the last element
while(left <= right){//If left > right subscript, it means that it is not found
int mid = (left + right)/2;//Find middle subscript
if(arr[mid]==target){//If found, returns the subscript
return mid;
}else if(arr[mid]>target){//If it's bigger than what you're looking for, go to the left
right = mid-1;
}else{//Or go to the right
left = mid+1;
}
}
//If not found, - 1 is returned
return -1;
}
}
5. Divide and conquer algorithm
1. Tower of Hanoi

- Operation effect
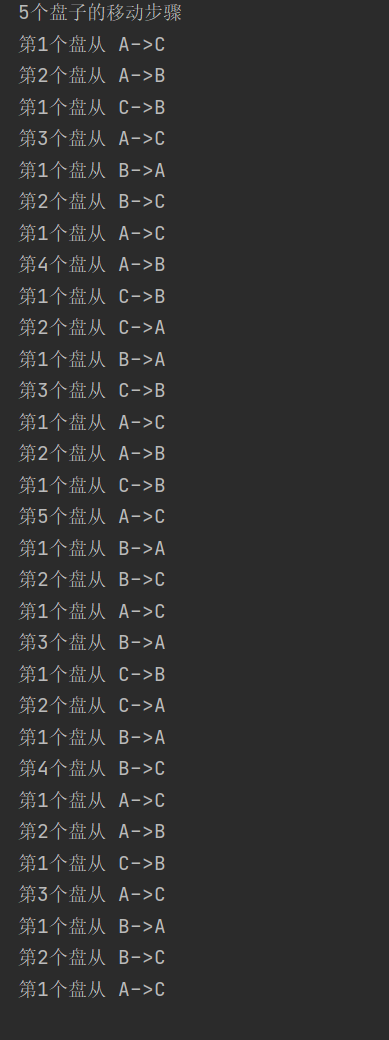
- code
public class Test {
public static void main(String[] args) {
System.out.println("5 Moving steps of two plates");
hanoiTower(5,'A','B','C');
}
/**
* For example, if we want to move the two disks in A to C, we need to first move the upper disk to B, then move the lower disk to C, and then move the disk just moved to B to C
* @param num Which disc
* @param a The position of the disc to be moved
* @param b Location to use
* @param c Location to move to
*/
public static void hanoiTower(int num,char a,char b,char c){
//If there is only one disk, there is no need to divide, because it is already the smallest unit. Start managing it and move directly from a to c
if(num == 1)
System.out.println("1st disk from "+a+"->"+c);
else{
//If there is more than one plate, we use the divide and conquer idea to divide all the plates into two parts, the bottom plate and all the plates above
//First move all the disks above from A to B, and move them with the help of C
hanoiTower(num-1,a,c,b);
//The lower disk, move from A to C
System.out.println("The first"+num+"Disk from "+a+"->"+c);
//Finally, move all the trays of Tower B to tower C and move them with the help of tower A
hanoiTower(num-1,b,a,c);
}
}
}
6. Dynamic planning

| Any dynamic transfer equation of dynamic programming is the derivation of violent recursive process |
|---|
| As long as there are repeated calculations, we need dynamic programming to avoid these repeated calculations |
|---|
| All violent recursion are ideas, which does not mean that problems can be solved, because violent recursion and its memory consumption are likely to overflow, just to let you know that if you deduce dynamic programming through simpler violent recursion |
|---|
1. Knapsack problem
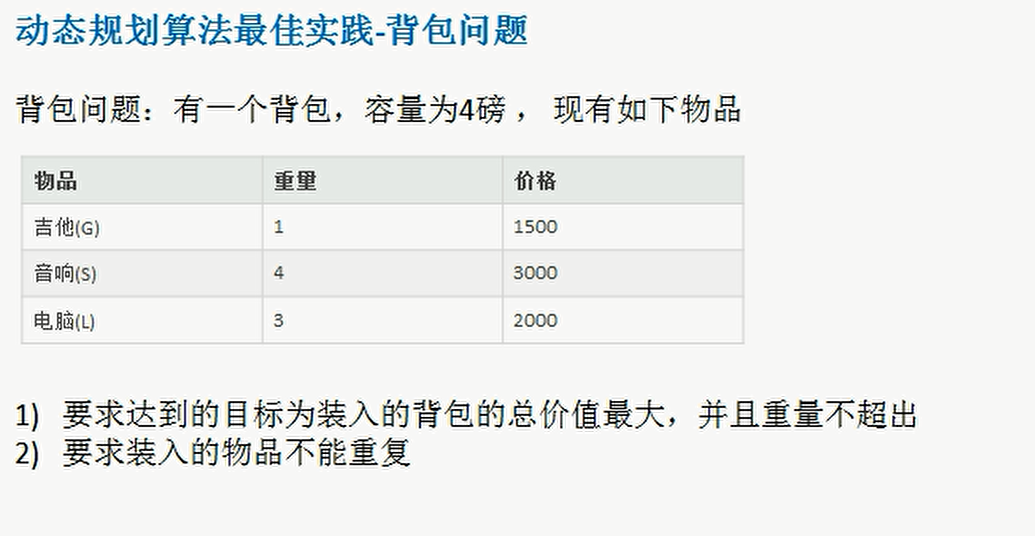
- There is a pile of items, each with its own weight w and value v
- We have a backpack. The maximum loading weight of the backpack is rest
- Find out how to load items in the backpack to maximize the value of items in the backpack
| Firstly, the violence recursion method is studied |
|---|
public class Main {
/**
* Left to right model
* For each item, calculate whether to add the current item to the backpack or not, and finally choose the larger value of the two schemes (note that this is recursion, and each recursion will return the larger value)
* @param w Item weight
* @param v Value of goods
* @param index Current item subscript
* @param rest Spare space of backpack
* @return
*/
public static int process(int[] w,int[] v,int index,int rest){
if(rest < 0) return -1;//If the remaining space of the backpack is less than 0, it means it can't be put at all. Return - 1 to indicate it can't be put
if(index == w.length) return 0;//If index == w.length, it indicates that there are no items. It is a recursive exit condition
//There are goods and space
int p1 = process(w,v,index + 1,rest);//The first status indicates that the current subscript item is not put into the backpack, so the current Backpack Capacity rest does not need to be reduced
int p2 = -1;//It is used to save items in the backpack. It is not valid by default
int p2Next = process(w,v,index + 1,rest - w[index]);//The second status indicates that the current subscript items are put into the backpack, and rest needs to be reduced
if(p2Next != -1){//If the scheme in the second state returns not - 1, it indicates that the scheme is feasible, and the value to p2 is increased
p2 = v[index] + p2Next;//Increase the value of current items
}
return Math.max(p1,p2);//Returns the maximum value of the first state and the second state
}
public static void main(String[] args) {
int[] w = {12,13,15,27,36,48};
int[] v = {10,5,27,58,100,100};
System.out.println(process(w,v,0,50));
}
}
- First, we find that in the process of violent recursion, there are only two values that always change, the current item index and the rest space of the backpack
- Suppose that we encounter the case that the current item subscript is 5 and the remaining space of the backpack is 10 many times in recursion, then we will save the process f(5,10)=x when we encounter this situation for the first time. When we encounter it for the second time, we find that f(5,10)=x has been cached, so we can directly obtain the X result without entering recursion again
- So we use a two-dimensional table to store these results. Imagine using index as the x-axis coordinate and rest as the y-axis coordinate (if you use an array, it is arr [index] [rest])
- Then we need to specify the size of the two-dimensional table. We found that if we want to fully store the results, we only need to define the two-dimensional table as arr [number of items] [maximum backpack space], and all the results can be stored
- However, in recursion, the exit condition of recursion is index == w.length; This shows that in addition to the number of items, we also use a value more than the number of items as the condition for us to exit recursion, so we also need to store it in the two-dimensional table, which is defined as arr [number of items + 1] [maximum space of backpack]
- Similarly, we need the maximum space for the backpack. Here, consider the case of 0, so we want to define it as arr [number of items + 1] [maximum space for the backpack + 1]
- Good dynamic programming is to draw a two-dimensional table with known information (of course, it may be a one-dimensional table according to different problems, which is simpler), and then return the result, that is, there is no need for recursion. The most common is to directly build a two-dimensional table with two for loops,
- We know that the final knapsack capacity is 0 and the last row of index is 0, so we can build a 2-dimensional table from bottom to top by using the known 0
| In the following code, if you are careful, you will find that in violent recursion, all return values are the values you want to add to the table structure during dynamic planning, and our violent recursion generates the structure from top to bottom, right to left, and the bottom and left are the final fixed value 0 Therefore, in dynamic programming, we can use the known condition 0 to generate a two-dimensional table from bottom to top and from left to right |
|---|
public class Main {
/**
*
* @param w Item weight
* @param v Value of goods
* @param bag Current Backpack Capacity
* @return
*/
public static int process(int[] w,int[] v,int bag){
int N = w.length;
int[][] dp = new int[N+1][bag+1];//Save the dynamic planning results. The default value is 0, so we have planned all 0 cases of the two-dimensional table
//The next step is to use dynamic programming to complete exactly the same functions as violent recursion
for(int index = N - 1;index >= 0 ;index--){//From bottom to top, traverse each row in turn, because the last row is exit 0 during violent recursion. We have just completed initialization
for(int rest = 1;rest <= bag;rest++){//Traverse each column from left to right. Similarly, 0 has been initially completed, and you can directly traverse 1
dp[index][rest] = dp[index + 1][rest];//p1 is equivalent to violent recursion, that is, the current item is not added to the backpack, but to think about the next item, so index+1
if(rest >= w[index]){//If the rest is larger than the required capacity of the current item, it means that the current item can be put into the backpack
//v[index]+dp[index+1][rest-w[index]] is equivalent to violent recursive p2, which stores the current items into the backpack, and the backpack capacity is reduced
//Then you can get the current situation value and select the largest one of p1 and p2
dp[index][rest] = Math.max(dp[index][rest],v[index]+dp[index+1][rest-w[index]]);
}
}
}
return dp[0][bag];//Violent recursion finally returns the result, corresponding to the elements in the upper right corner of the two-dimensional table
}
public static void main(String[] args) {
int[] w = {12,13,15,27,36,48};
int[] v = {10,5,27,58,100,100};
System.out.println(process(w,v,50));
}
}
2. Change problem
- Given an arr array, all values are positive without repetition, representing a currency with face value, and the number of currencies is not specified
- Use the variable aim to represent the amount of money you want to find
- Find out how many ways to change money. Use different amounts of money to find the same money
- As soon as you look at the question, you can guess that the ordinate of the two-dimensional table is the face value of the coin, the abscissa is the number of pieces, and the value is the amount of money
- make a concrete analysis
- First of all, we know the size of money (assumed to be rest), but there is no requirement for money
- The best way is to use rest - current face value every time we recurse. When rest==0, it means that the requirements are met
| Here's how to step by step from violent recursion - > memory search - > fine dynamic planning. And the time consumed by the three algorithms |
|---|
package com.company;
import java.util.Date;
public class Main {
public static int dfs(int arr[],int index,int rest){
if(rest < 0) return 0;//In fact, this sentence is useless, because the for loop has solved this problem. If the remaining money is less than 0, it means that the amount of money is exceeded, and then 0 is returned, indicating that this method does not work
//If the money is not less than 0, it means there is still a chance to get the correct answer. We judge idnex == arr.length to see if there is any money. If it is equal, it means there is no money
if(index == arr.length) return rest==0?1:0;//If the current rest is already 0, it means that the requirements are met and returns 1. Otherwise, because there is no money, this method does not work and returns 0
int ways = 0;//Number of recording methods
//Because we do not specify the quantity of each currency, the use range of each currency is 0~n, but it is necessary to meet the n * currency face value < rest, that is, use as many as you like, but not more than the current remaining money
for(int i =0;(arr[index]*i)<=rest;i++){//The for loop here has guaranteed that no matter how you choose, it cannot exceed the current amount of money left, so the first sentence of this method is actually useless
ways+=dfs(arr,index+1,rest-(arr[index]*i));//Proceed to the next denomination currency, and rest will subtract the amount of money used in the current currency
}
return ways;
}
/**Top down dynamic programming
* Optimize violence recursion with mnemonic search
* If the current index=3 and rest=900, we will record dp[3][900] = results
* @param dp Represents a cache table
*/
public static int dp1(int arr[],int index,int rest,int dp[][]){
if(dp[index][rest]!=-1) return dp[index][rest];//If this status has been calculated in the cache table, the value will be taken directly
if(index == arr.length) {
dp[index][rest]=(rest==0?1:0);
return dp[index][rest];
}
int ways = 0;
for(int i =0;(arr[index]*i)<=rest;i++){
ways+=dp1(arr,index+1,rest-(arr[index]*i),dp);
}
dp[index][rest]=ways;
return dp[index][rest];
}
/**Bottom up dynamic programming
* Fine dynamic programming
*
*/
public static int dp2(int arr[],int aim){
int N = arr.length;
int[][] dp2 = new int[N+1][aim+1];
//According to the two-dimensional table derived by violence recursion, it can be found that the last row is the end condition of recursion,
// However, if the first note is used enough times, the result is 1, so the N-th line (the last line) is 0 except that the first position is 1
dp2[N][0]=1;
//Secondly, according to violent recursion, we can see that the value of any line needs the value of + 1 of the current line, which has nothing to do with the line, so we can push the penultimate line through the last line, that is, to meet the bottom-up requirements
for(int index=N-1;index>=0;index--){//Bottom up
for(int rest = 0;rest<=aim;rest++){//From left to right
//int ways = 0;
//for(int i =0;(arr[index]*i)<=rest;i++){
// ways+=dp1(arr,index+1,rest-(arr[index]*i),dp);
//}
//You can deduce dp2[index][rest] according to the above violent recursion, but there will be enumeration problems. For example, I need to calculate the values of all DP2 [4] [0... 5],
//However, these values have been calculated at dp2[5][4], so they are calculated repeatedly. On the contrary, the efficiency is not as good as using memory search to optimize violence recursion
// for(int i = 0;(arr[index]*i)<=rest;i++){
// dp2[index][rest]=dp2[index][rest]+dp2[index+1][rest-(arr[index]*i)];
// }
//To solve the enumeration problem, dp2[5][5]==dp2[5][4]+dp2[4][5]
dp2[index][rest] = dp2[index+1][rest];
if(rest - arr[index]>=0){//If the subscript does not cross the boundary
dp2[index][rest] += dp2[index][rest-arr[index]];
}
}
}
return dp2[0][aim];
}
public static void main(String[] args) {
int arr[] = {5,10,50,100};
int aim = 9900;
/**Violent recursion*/
long start = new Date().getTime();
System.out.println(dfs(arr,0,aim));
long end = new Date().getTime();
System.out.println("Time taken (in milliseconds)"+(end-start));
/**Memory search**/
int dp[][] = new int[arr.length+1][aim+1];//Cache table
for(int i = 0 ;i<dp.length;i++){//All values in the initial state are not calculated, and all values are expressed as - 1
for (int j =0;j<dp[0].length;j++){
dp[i][j]=-1;
}
}
long start1 = new Date().getTime();
System.out.println(dp1(arr,0,aim,dp));
long end1 = new Date().getTime();
System.out.println("Time taken (in milliseconds)"+(end1-start1));
/**Fine dynamic programming**/
long start2 = new Date().getTime();
System.out.println(dp2(arr,aim));
long end2 = new Date().getTime();
System.out.println("Time taken (in milliseconds)"+(end2-start2));
}
}
7. KMP algorithm
- It is a classical algorithm to solve whether the pattern string has appeared in the text string, and if so, to obtain the earliest position
- It is often used to find the position of a pattern string P in a text string S. This algorithm was jointly published by Donald Knuth, Vaughan Pratt and James H.Morris in 1977. Therefore, the surnames of the three people are named Knuth Morris Pratt, which is referred to as KMP algorithm for short
- Using the previously judged information, save the length of the most common subsequence before and after the pattern string through a next array. During each backtracking, find the previously matched position through the next array, saving a lot of calculation time













- Operation effect

- code
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
// TODO Auto-generated method stub
String str1 = "BBC ABCDAB ABCDABCDABDE";
String str2 = "ABCDABD";
//String str2 = "BBC";
int[] next = kmpNext("ABCDABD"); //[0, 1, 2, 0]
System.out.println("next=" + Arrays.toString(next));
int index = kmpSearch(str1, str2, next);
System.out.println("index=" + index); // 15
}
//Gets the partial matching value table of a string (substring)
public static int[] kmpNext(String dest) {
//Create a next array to hold some matching values
int[] next = new int[dest.length()];
next[0] = 0; //If the string is a length of 1, the matching value is 0
//We should traverse the string in turn, remove the A with the length of the above string of 1, cycle AB for the first time and ABC for the second time, and record when the suffix and prefix have the same string. i represents the length of the string, j represents the length of the prefix when the front and back affixes are the same
for(int i = 1, j = 0; i < dest.length(); i++) {
//When dest charAt(i) != dest. Charat (J), we need to get a new j from next[j-1]
//Until we found dest charAt(i) == dest. Charat (J) is established before exiting
//This is the core of kmp algorithm
//For example, when i=4, j=0 The substring is ABCDA. At this time, A==A, exit the loop - for example, when i=5, j=1, and the substring is ABCDAB. At this time, because A==A was compared last time, there is no need to compare. Directly B==B, exit the loop
while(j > 0 && dest.charAt(i) != dest.charAt(j)) {
j = next[j-1];
}
//When dest charAt(i) == dest. When charat (J) is satisfied, the partial matching value is + 1
//A==A-----B==B
if(dest.charAt(i) == dest.charAt(j)) {
j++;
}
//next[4]=1;===next[5] == 2
next[i] = j;
}
return next;
}
//Write our kmp search algorithm
/**
*
* @param str1 Source string
* @param str2 Substring
* @param next The partial matching table is the partial matching table corresponding to the substring
* @return If it is - 1, there is no match. Otherwise, the first matching position is returned
*/
public static int kmpSearch(String str1, String str2, int[] next) {
//ergodic
for(int i = 0, j = 0; i < str1.length(); i++) {
//STR1. Needs to be processed charAt(i) != str2.charAt(j), to adjust the size of j
//KMP algorithm core point, can verify
//String str1 = "BBC ABCDAB ABCDABCDABDE";
// String str2 = "ABCDABD";
//Matching table next=[0, 0, 0, 0, 1, 2, 0]
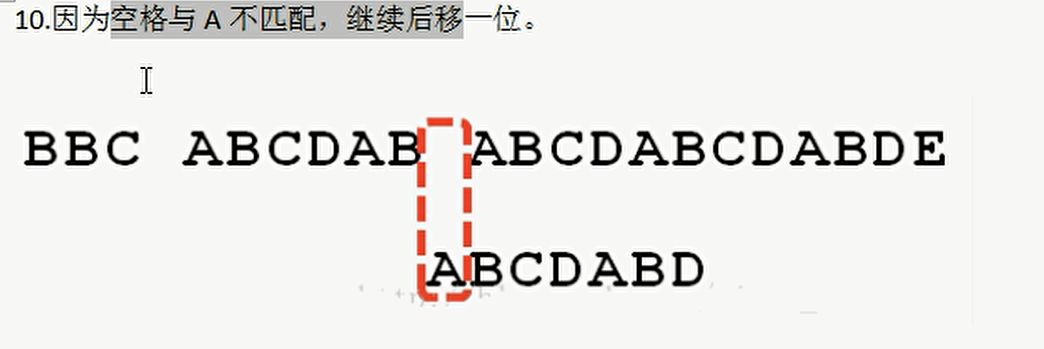
//When I = 10 and j = 6, the preceding ABCDAB matches successfully, but now the spaces compare D and are not equal. At this time, it indicates that it is not a substring
//At this time, enter the loop, j = 2, compare the spaces and C, which are not equal, and then enter the loop
//j = 1, compare the space and B, not equal, and then enter the loop
//j = 0, if the condition is not met, exit the cycle
//Next time, the matching will continue after the space to avoid repeated comparison
while( j > 0 && str1.charAt(i) != str2.charAt(j)) {
j = next[j-1];
}
//
if(str1.charAt(i) == str2.charAt(j)) {
j++;
}
if(j == str2.length()) {//Found / / j = 3 i
return i - j + 1;
}
}
return -1;
}
}
8. Greedy algorithm

- Greedy algorithm is to find the optimal solution. There is no optimal solution, only better
- Generally, arrays and sequences are sorted according to rules, and then recursively or circularly traversed to find the optimal solution
- Operation effect

- code
import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
public class Test {
public static void main(String[] args) {
//Create a radio station and put it into the Map
HashMap<String,HashSet<String>> broadcasts = new HashMap<String, HashSet<String>>();
//Put each radio station into broadcasts
HashSet<String> hashSet1 = new HashSet<String>();
hashSet1.add("Beijing");hashSet1.add("Shanghai");hashSet1.add("Tianjin");
HashSet<String> hashSet2 = new HashSet<String>();
hashSet2.add("Guangzhou");hashSet2.add("Beijing");hashSet2.add("Shenzhen");
HashSet<String> hashSet3 = new HashSet<String>();
hashSet3.add("Chengdu");hashSet3.add("Shanghai");hashSet3.add("Hangzhou");
HashSet<String> hashSet4 = new HashSet<String>();
hashSet4.add("Shanghai");hashSet4.add("Tianjin");
HashSet<String> hashSet5 = new HashSet<String>();
hashSet5.add("Hangzhou");hashSet5.add("Dalian");
//Add to map
broadcasts.put("K1", hashSet1);broadcasts.put("K2", hashSet2);broadcasts.put("K3", hashSet3);broadcasts.put("K4", hashSet4);broadcasts.put("K5", hashSet5);
//allAreas stores all areas
HashSet<String> allAreas = new HashSet<String>();
allAreas.add("Beijing");allAreas.add("Shanghai");allAreas.add("Tianjin");allAreas.add("Guangzhou");allAreas.add("Shenzhen");allAreas.add("Chengdu");allAreas.add("Hangzhou");allAreas.add("Dalian");
//Create an ArrayList to store the selected radio station collection
ArrayList<String> selects = new ArrayList<String>();
//Define a temporary set to store the intersection of the area covered by the radio station during the traversal and the area not covered at present
HashSet<String> tempSet = new HashSet<String>();
//Defined to maxKey and saved in one traversal process, the key of the radio station corresponding to the largest uncovered area can be covered
//If the maxKey is not null, it will be added to the selections
String maxKey = null;
while(allAreas.size() != 0) { // If allAreas is not 0, it means that all regions have not been covered
//For each while, you need to
maxKey = null;
//Traverse broadcasts and get the corresponding key
for(String key : broadcasts.keySet()) {
//Every time
tempSet.clear();
//The area that this key can cover at present
HashSet<String> areas = broadcasts.get(key);
tempSet.addAll(areas);
//Find the intersection of tempSet and allAreas set, and the intersection will be assigned to tempSet
tempSet.retainAll(allAreas);
//If the current collection contains more uncovered regions than the collection region pointed to by the maxKey
//You need to reset the maxKey
// tempSet. size() >broadcasts. get(maxKey). Size () reflects the characteristics of greedy algorithm and selects the best one every time
if(tempSet.size() > 0 &&
(maxKey == null || tempSet.size() >broadcasts.get(maxKey).size())){
maxKey = key;
}
}
//maxKey != null, you should add maxkey to selections
if(maxKey != null) {
selects.add(maxKey);
//Remove the area covered by the radio station pointed to by maxKey from allAreas
allAreas.removeAll(broadcasts.get(maxKey));
}
}
System.out.println("The selection result is" + selects);//[K1,K2,K3,K5]
}
}
9. Minimum spanning tree algorithm
1. Prim algorithm
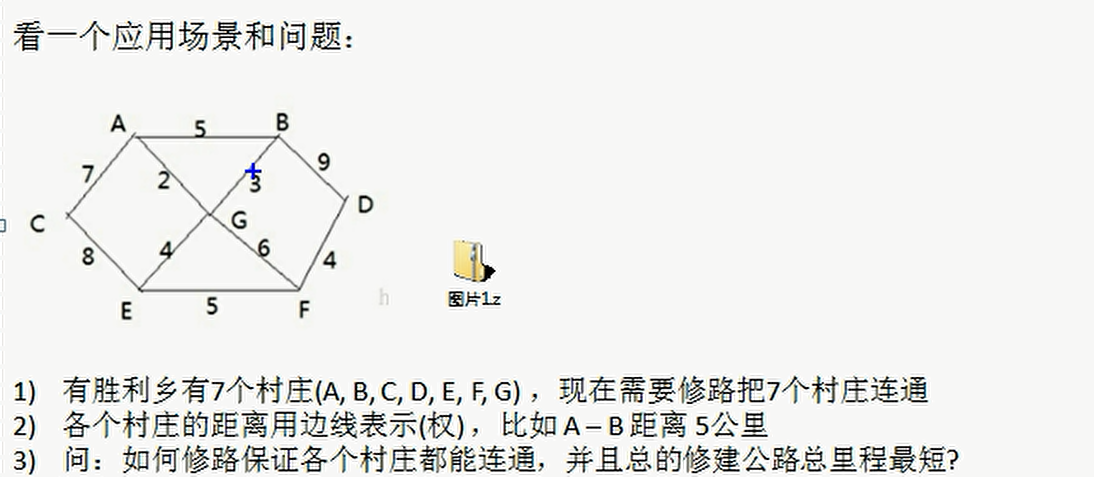
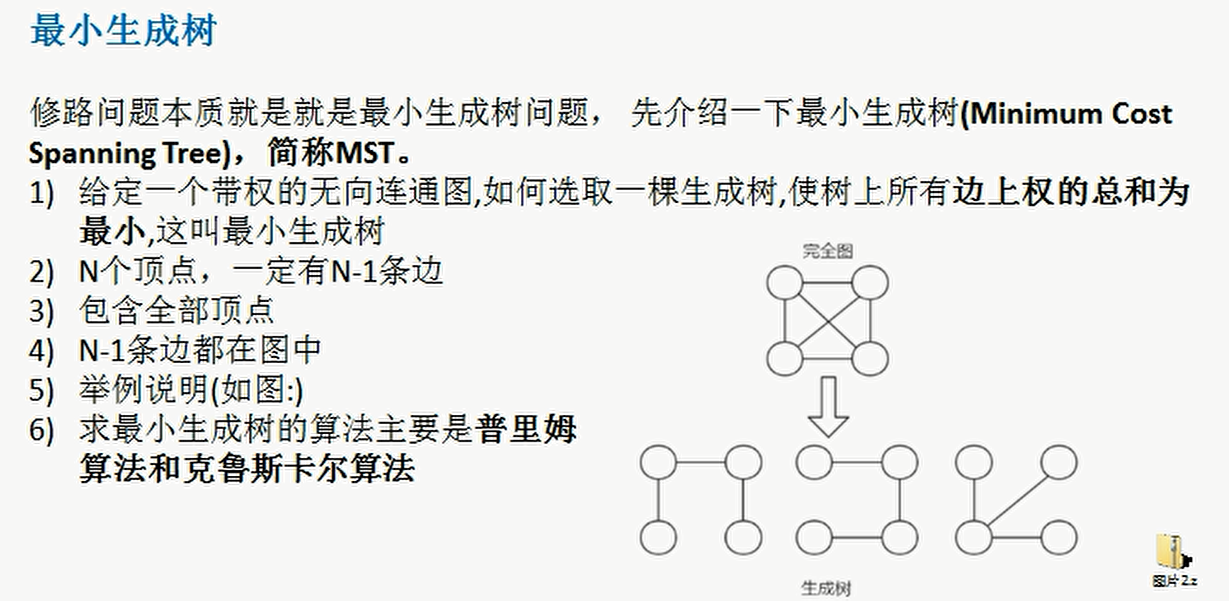
- The essence of the road construction problem is the Minimum Cost Spanning Tree problem (MST).
- Given a weighted undirected connected graph, how to select a spanning tree to minimize the sum of weights on all edges of the tree is called the minimum spanning tree
- N vertices must have N-1 edges
- And connected all vertices
- These N-1 edges are all in a complete graph
- The algorithms for finding the minimum spanning tree mainly include prim algorithm and Kruskal algorithm
- Finding the minimum spanning tree is to find the connected subgraph in which only n-1 edges connect all vertices in the connected graph containing n vertices, that is, the minimum connected subgraph
- The algorithm idea is as follows:

- Let G=(V,E) be a connected graph, T=(U,D) be a minimum spanning tree, V,U be a set of vertices, and E,D be a set of edges
- If the minimum spanning tree is constructed from vertex a, take vertex a from set V and put it into set U. mark vertex a with visited[a]=1, indicating that it has been accessed. If it is not the first construction, select an edge that has not been accessed, and then find the edge with the smallest weight
- If there are edges between vertex B in set V and vertex a in set U, find the edge with the smallest weight among these edges, but it can not form a loop. Add vertex a to set U and edge (a, b) to set D. the mark visited[b]=1 indicates that this vertex B has also been visited
- Repeat step 2 until U and V are equal, that is, all vertices are marked as visited, and there are n-1 edges in D
package com.yzpnb.test;
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
//Test to see if the diagram is created ok
char[] data = new char[]{'A','B','C','D','E','F','G'};
int verxs = data.length;
//The adjacency matrix is represented by a two-dimensional array. The large number of 10000 indicates that the two points are not connected
int [][]weight=new int[][]{
{10000,5,7,10000,10000,10000,2},
{5,10000,10000,9,10000,10000,3},
{7,10000,10000,10000,8,10000,10000},
{10000,9,10000,10000,10000,4,10000},
{10000,10000,8,10000,10000,5,4},
{10000,10000,10000,4,5,10000,6},
{2,3,10000,10000,4,6,10000},};
//Create MGraph object
MGraph graph = new MGraph(verxs);
//Create a MinTree object
MinTree minTree = new MinTree();
minTree.createGraph(graph, verxs, data, weight);
//output
minTree.showGraph(graph);
//Test prim algorithm
minTree.prim(graph, 1);//
}
}
//Create a graph of minimum spanning tree - > Village
class MinTree {
//Create adjacency matrix of graph
/**
*
* @param graph Graph object
* @param verxs Number of vertices corresponding to graph
* @param data The value of each vertex of the graph
* @param weight adjacency matrix
*/
public void createGraph(MGraph graph, int verxs, char data[], int[][] weight) {
int i, j;
for(i = 0; i < verxs; i++) {//vertex
graph.data[i] = data[i];
for(j = 0; j < verxs; j++) {
graph.weight[i][j] = weight[i][j];
}
}
}
//Show adjacency matrix of graph
public void showGraph(MGraph graph) {
for(int[] link: graph.weight) {
System.out.println(Arrays.toString(link));
}
}
//Write prim algorithm to get the minimum spanning tree
/**
*
* @param graph chart
* @param v Indicates that 'a' - > 0 'B' - > 1 is generated from the first vertex of the graph
*/
public void prim(MGraph graph, int v) {
//visited [] mark whether the node (vertex) has been accessed
int visited[] = new int[graph.verxs];
//visited [] the value of the default element is 0, indicating that it has not been accessed
// for(int i =0; i <graph.verxs; i++) {
// visited[i] = 0;
// }
//Mark the current node as accessed
visited[v] = 1;
//h1 and h2 record the subscripts of the two vertices
int h1 = -1;
int h2 = -1;
int minWeight = 10000; //Initial minWeight to a large number, which will be replaced later in the traversal process
for(int k = 1; k < graph.verxs; k++) {//Because there is a graph Verxs vertex, after the end of prim algorithm, there is graph Verxs-1 side
//This is to determine which node is closest to each generated subgraph
for(int i = 0; i < graph.verxs; i++) {// i node represents the visited node
for(int j = 0; j< graph.verxs;j++) {//The j node represents a node that has not been accessed
//Get the edge with the smallest weight and two vertex subscripts
if(visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < minWeight) {
//Replace minweight (find the edge with the smallest weight between the visited node and the unreached node)
minWeight = graph.weight[i][j];
h1 = i;
h2 = j;
}
}
}
//Find an edge that is the smallest
System.out.println("edge<" + graph.data[h1] + "," + graph.data[h2] + "> Weight :" + minWeight);
//Mark the current node as accessed
visited[h2] = 1;
//Reset minWeight to a maximum of 10000
minWeight = 10000;
}
}
}
/**
* Data structure diagram
*/
class MGraph{
int verxs;//Number of nodes of graph
char[] data;//Store node data
int[][] weight;//adjacency matrix
public MGraph(int verxs) {
this.verxs = verxs;
data = new char[verxs];
weight = new int[verxs][verxs];
}
}
2. Kruskal algorithm
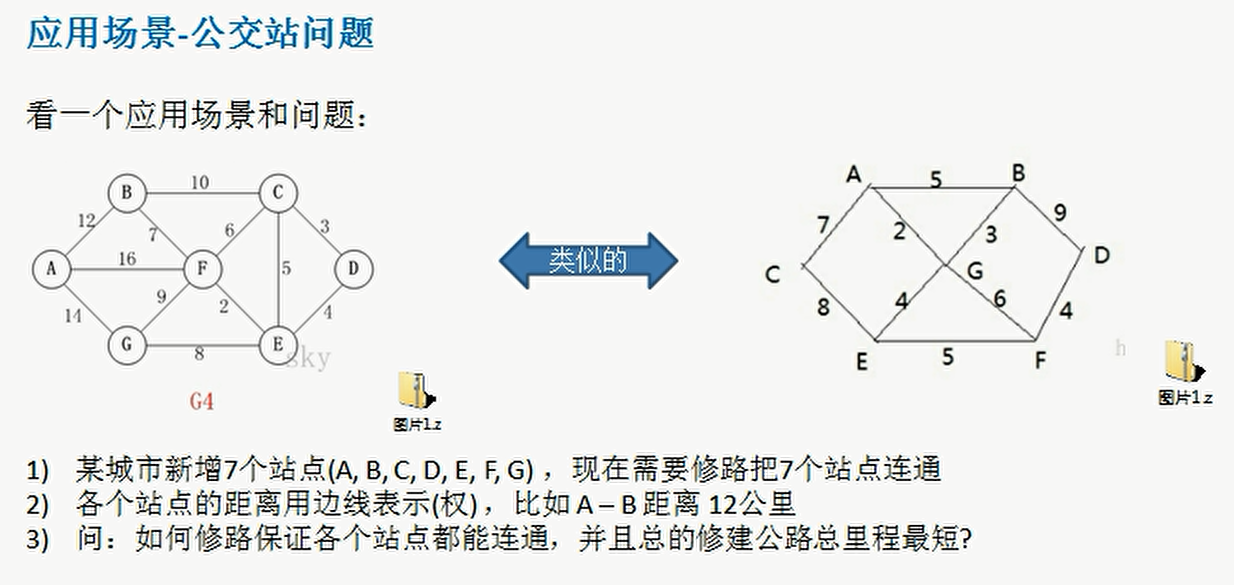
- Kruskal algorithm is used to find the minimum spanning tree of weighted connected graph
- Select n-1 edges in the order of weight from small to large to ensure that n-1 edges do not form a loop
- Firstly, a forest with only n vertices is constructed, and then edges are selected from the connected graph to join the forest according to the weight from small to large, so that there is no loop in the forest until the forest becomes a class tree
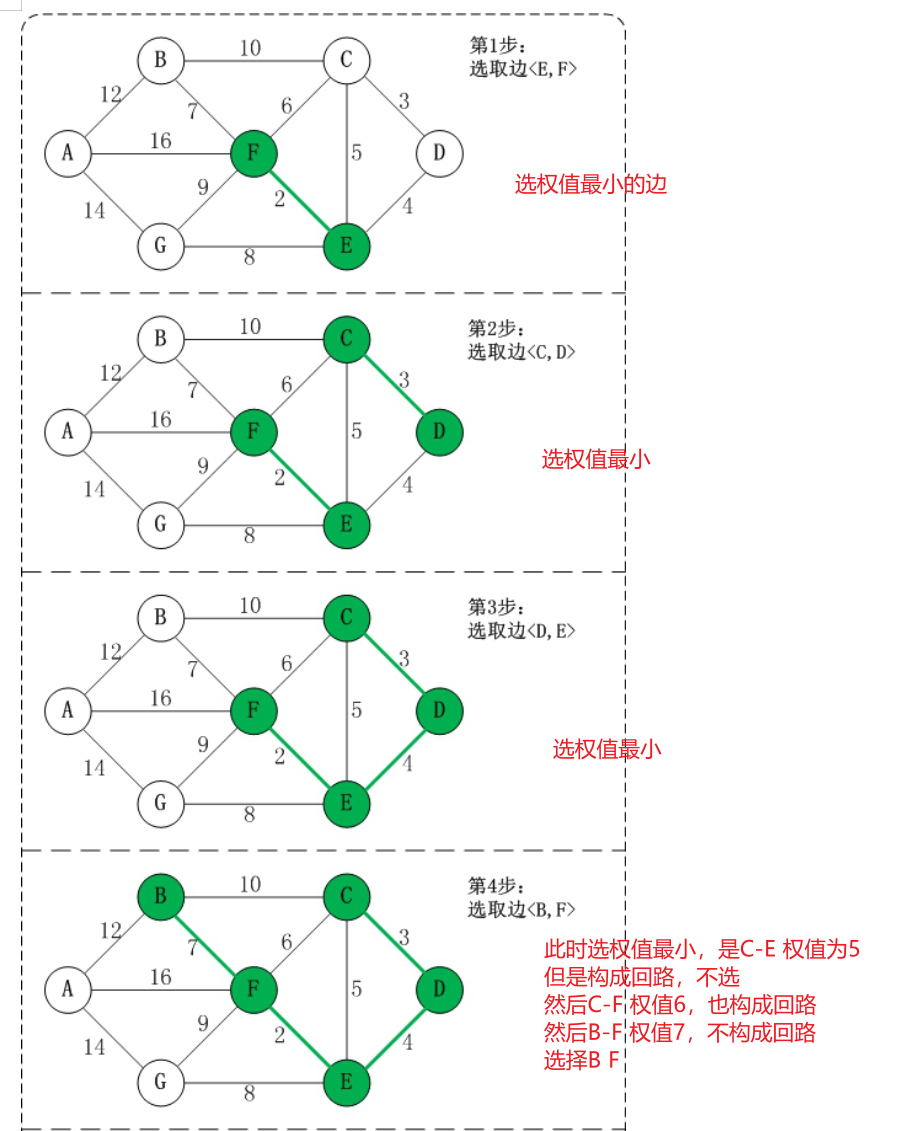
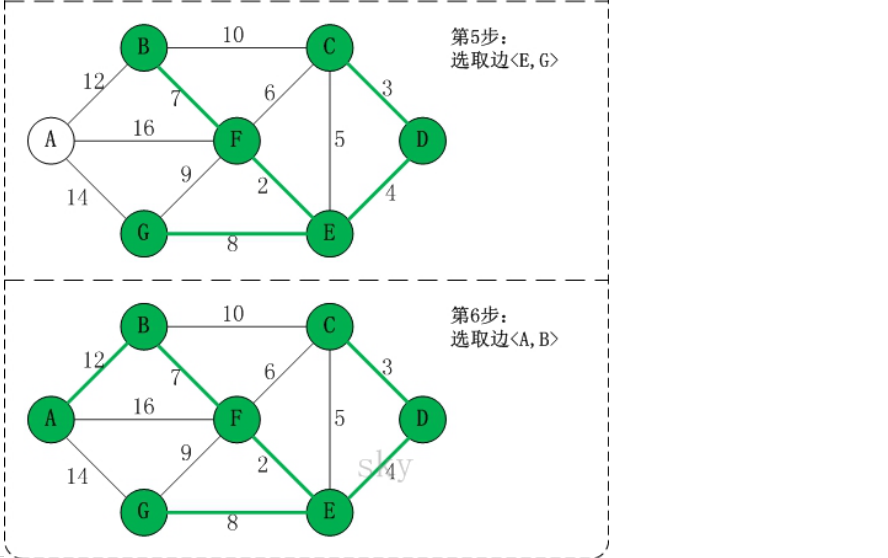
| How to judge whether a circuit is formed |
|---|
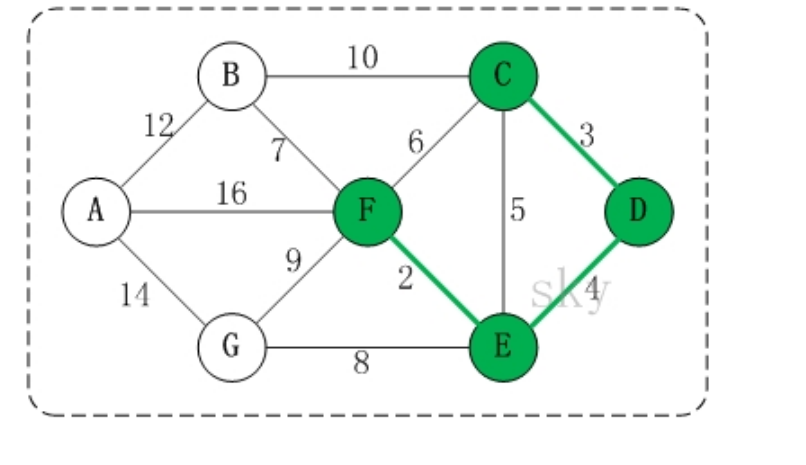
- After adding < e, f > < C, d > < D, E > to the minimum spanning tree R, the vertices of these edges have endpoints
- The end point of C is F.
- The end point of D is F.
- The end point of E is F.
- The end of F is f.
- End
- After arranging all the vertices added to the minimum spanning tree R in the order from small to large; The end point of a vertex is the "largest vertex connected to it"
- Therefore, next, although < C, E > is the edge with the smallest weight. However, the endpoints of C and E are both F, that is, their endpoints are the same. Therefore, adding < C, E > to the minimum spanning tree will form a loop. This is the way to judge the loop
- The two vertices of the edge we join cannot both point to the same end point, otherwise it will form a loop
import java.util.Arrays;
public class Test {
//Use INF to indicate that two vertices cannot be connected
private static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//Adjacency matrix of Kruskal algorithm
int matrix[][] = {
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/ { 0, 12, INF, INF, INF, 16, 14},
/*B*/ { 12, 0, 10, INF, INF, 7, INF},
/*C*/ { INF, 10, 0, 3, 5, 6, INF},
/*D*/ { INF, INF, 3, 0, 4, INF, INF},
/*E*/ { INF, INF, 5, 4, 0, 2, 8},
/*F*/ { 16, 7, 6, INF, 2, 0, 9},
/*G*/ { 14, INF, INF, INF, 8, 9, 0}};
//You can test other adjacency matrices and get the minimum spanning tree
//Create KruskalCase object instance
KruskalCase kruskalCase = new KruskalCase(vertexs, matrix);
//Output built
kruskalCase.print();
kruskalCase.kruskal();
}
}
class KruskalCase{
private int edgeNum; //Number of edges
private char[] vertexs; //vertex array
private int[][] matrix; //adjacency matrix
//Use INF to indicate that two vertices cannot be connected
private static final int INF = Integer.MAX_VALUE;
//constructor
public KruskalCase(char[] vertexs, int[][] matrix) {
//Initializes the number of vertices and edges
int vlen = vertexs.length;
//Initialize vertices and copy
this.vertexs = new char[vlen];
for(int i = 0; i < vertexs.length; i++) {
this.vertexs[i] = vertexs[i];
}
//The edge is initialized by copying
this.matrix = new int[vlen][vlen];
for(int i = 0; i < vlen; i++) {
for(int j= 0; j < vlen; j++) {
this.matrix[i][j] = matrix[i][j];
}
}
//Count the number of edges
for(int i =0; i < vlen; i++) {
for(int j = i+1; j < vlen; j++) {
if(this.matrix[i][j] != INF) {
edgeNum++;
}
}
}
}
public void kruskal() {
int index = 0; //Represents the index of the last result array
int[] ends = new int[edgeNum]; //Used to save the end point of each vertex in the existing minimum spanning tree in the minimum spanning tree
//Create a result array and save the last minimum spanning tree
EData[] rets = new EData[edgeNum];
//Get the set of all edges in the graph, with a total of 12 edges
EData[] edges = getEdges();
System.out.println("Set of edges of Graphs=" + Arrays.toString(edges) + " common"+ edges.length); //12
//Sort according to the weight of edges (from small to large)
sortEdges(edges);
//When traversing the edges array and adding edges to the minimum spanning tree, judge whether the edges to be added form a loop. If not, add rets, otherwise they cannot be added
for(int i=0; i < edgeNum; i++) {
//Gets the first vertex (starting point) to the ith edge
int p1 = getPosition(edges[i].start); //p1=4
//Gets the second vertex of the i th edge
int p2 = getPosition(edges[i].end); //p2 = 5
//Get p1 the endpoint of this vertex in the existing minimum spanning tree
int m = getEnd(ends, p1); //m = 4
//Get p2 the endpoint of this vertex in the existing minimum spanning tree
int n = getEnd(ends, p2); // n = 5
//Does it constitute a loop
if(m != n) { //No loop
ends[m] = n; // Set the end point of m in the existing minimum spanning tree < e, f > [0,0,0,0,5,0,0,0,0,0,0,0]
rets[index++] = edges[i]; //An edge is added to the rets array
}
}
//<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>.
//Count and print the "minimum spanning tree" and output rets
System.out.println("The minimum spanning tree is");
for(int i = 0; i < index; i++) {
System.out.println(rets[i]);
}
}
//Print adjacency matrix
public void print() {
System.out.println("Adjacency matrix is: \n");
for(int i = 0; i < vertexs.length; i++) {
for(int j=0; j < vertexs.length; j++) {
System.out.printf("%12d", matrix[i][j]);
}
System.out.println();//Line feed
}
}
/**
* Function: sort the edges, bubble sort
* @param edges Set of edges
*/
private void sortEdges(EData[] edges) {
for(int i = 0; i < edges.length - 1; i++) {
for(int j = 0; j < edges.length - 1 - i; j++) {
if(edges[j].weight > edges[j+1].weight) {//exchange
EData tmp = edges[j];
edges[j] = edges[j+1];
edges[j+1] = tmp;
}
}
}
}
/**
*
* @param ch Vertex values, such as' A','B '
* @return Returns the subscript corresponding to the ch vertex. If not found, returns - 1
*/
private int getPosition(char ch) {
for(int i = 0; i < vertexs.length; i++) {
if(vertexs[i] == ch) {//find
return i;
}
}
//Cannot find, return - 1
return -1;
}
/**
* Function: get the edges in the graph and put them into the EData [] array. Later, we need to traverse the array
* It is obtained by matrix adjacency matrix
* EData[] Form [['A','B', 12], ['B','F',7],...]
* @return
*/
private EData[] getEdges() {
int index = 0;
EData[] edges = new EData[edgeNum];
for(int i = 0; i < vertexs.length; i++) {
for(int j=i+1; j <vertexs.length; j++) {
if(matrix[i][j] != INF) {
edges[index++] = new EData(vertexs[i], vertexs[j], matrix[i][j]);
}
}
}
return edges;
}
/**
* Function: obtain the end point () of the vertex with subscript i, which is used to judge whether the end points of the two vertices are the same
* @param ends : The array records the corresponding end point of each vertex. The ends array is gradually formed during traversal
* @param i : Indicates the subscript corresponding to the incoming vertex
* @return What is returned is the subscript of the end point corresponding to the vertex with subscript i. i will understand later
*/
private int getEnd(int[] ends, int i) { // i = 4 [0,0,0,0,5,0,0,0,0,0,0,0]
while(ends[i] != 0) {
i = ends[i];
}
return i;
}
}
//Create a class EData whose object instance represents an edge
class EData {
char start; //A point on the edge
char end; //Another point on the edge
int weight; //Weight of edge
//constructor
public EData(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
//Rewrite toString to output edge information
@Override
public String toString() {
return "EData [<" + start + ", " + end + ">= " + weight + "]";
}
}
10. Dijestra algorithm (algorithm of graph data structure)

- Suppose A, B, C, D, E, F and G represent 6 villages. Now there are 6 postmen from G to ABCDEF
- The distance between each village is indicated by a sideline. For example, the distance between A-B is 5km
- How to calculate the shortest distance from G village to other villages? What is the shortest distance from other points to each point?
| Digkstra dijestra algorithm is a typical shortest path algorithm |
|---|
- It is used to calculate the shortest path from one node to other nodes. The main feature is to expand outward layer by layer centered on the starting point (breadth first search idea) until it is extended to the end point
- Specify the starting vertex g, define the vertex set V{A,B,C,D,E,F,G}, and define the distance set Dis{d1,d2,d3,d4,di...} composed of the distances from each vertex in G to v. the distance from point G to each vertex in the Dis set is recorded as 0
- Select the minimum di from Dis, move out of Dis set, and move out the corresponding vertex vi in V set, such as A. At this time, G to A is the shortest path
- Update the Dis set, compare the distance value from the vertices in the G to V set with the distance value from the G point passing through a point (assuming vi) to the target point (assuming P) (passing through a vertex and reaching the target point), keep the value small, and update the precursor node of the vertex as the point it passes through (the precursor of P is vi), and save it in an array or set
- Repeat steps 2-3 until the shortest path vertex is the target vertex

- Operation effect
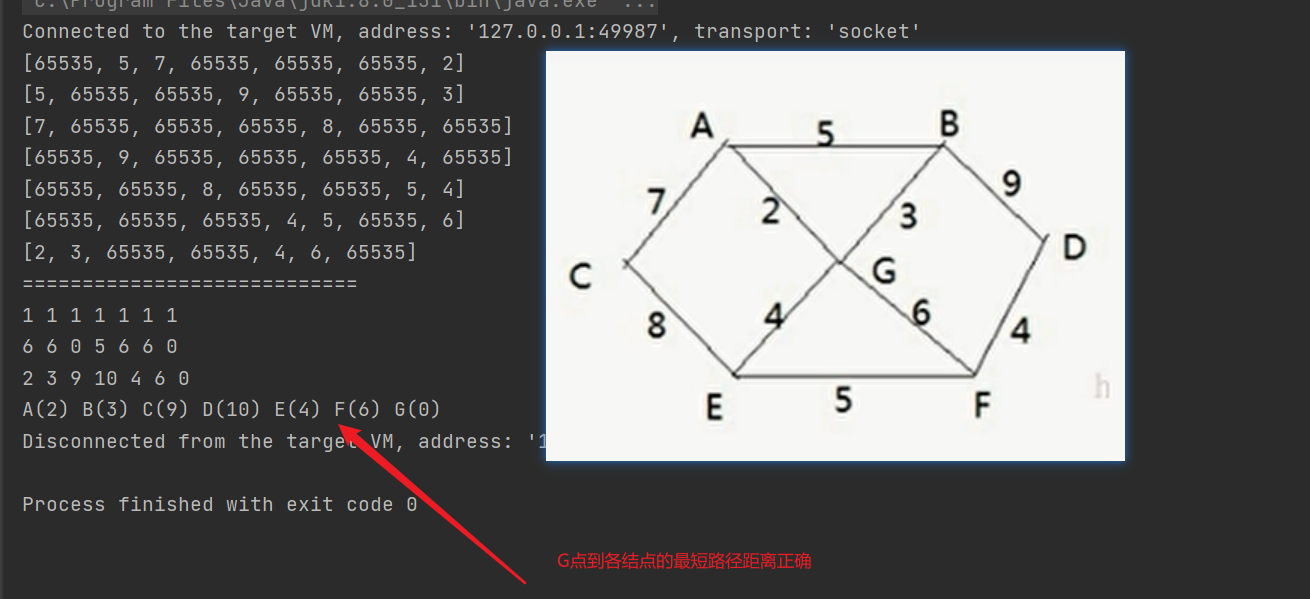
- code
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
//node
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
//adjacency matrix
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 65535;// Indicates that the connection is not possible
matrix[0]=new int[]{N,5,7,N,N,N,2};
matrix[1]=new int[]{5,N,N,9,N,N,3};
matrix[2]=new int[]{7,N,N,N,8,N,N};
matrix[3]=new int[]{N,9,N,N,N,4,N};
matrix[4]=new int[]{N,N,8,N,N,5,4};
matrix[5]=new int[]{N,N,N,4,5,N,6};
matrix[6]=new int[]{2,3,N,N,4,6,N};
//Create a Graph object
Graph graph = new Graph(vertex, matrix);
//Test to see if the adjacency matrix of the graph is ok
graph.showGraph();
//Test dijestra algorithm
graph.digkstra(6);
graph.showDijkstra();
}
}
class Graph{
private char[] vertex;//vertex array
private int[][] matrix;//Collar matrix
private VisitedVertex visitedVertex;//Nodes that have been accessed
//constructor
public Graph(char[] vertex,int[][] matrix){
this.vertex = vertex;
this.matrix = matrix;
}
//Display diagram
public void showGraph(){
for (int[] link: matrix){
System.out.println(Arrays.toString(link));
}
}
/**
* Dijkstra's algorithm
* @param index Starting vertex subscript
*/
public void digkstra(int index){
//Gets the access vertex and initializes the required collection
this.visitedVertex = new VisitedVertex(vertex.length, index);
update(index);//Update the distance from the index vertex to the surrounding vertex and the precursor vertex
//Updates the distance from the remaining vertices to the surrounding vertices and the leading vertices
for(int j = 1;j < vertex.length;j++){
index = visitedVertex.updateArr();//Select and return to the new access vertex
update(index);//Update the distance from the index vertex to the surrounding vertex and the precursor vertex
}
}
/**
* Update the distance from index subscript vertices to surrounding vertices and the precursor vertices of surrounding vertices
* @param index Specify vertex subscript
*/
private void update(int index){
int len = 0;//Distance from surrounding nodes
//Ergodic adjacency matrix, only ergodic and index vertex related, so you can directly ergodic index row
for(int j = 0;j<matrix[index].length;j++){
//Distance from the starting vertex to the current node + distance from the current node to each node (the adjacency matrix stores the distance to each node. The adjacent nodes will have a distance. If they are not adjacent, 65536 will not work)
len = visitedVertex.getDis(index) + matrix[index][j];
//If the j node is not accessed and len is less than the distance from the starting vertex to the j vertex (the initial distance is 65536 except from itself to itself), it needs to be updated
//If len < visitedvertex Getdis (J) is satisfied, indicating that the current node and j node can communicate
if(!visitedVertex.isVisited(j) && len < visitedVertex.getDis(j)){
visitedVertex.updatePre(j,index);//Set the precursor of the j vertex to index
visitedVertex.updateDis(j,len);//Set the distance from the departure node to the j node
}
}
}
public void showDijkstra(){
visitedVertex.show();
}
}
//The node class that has been accessed stores the collection required by the algorithm
class VisitedVertex{
//Record whether each vertex has been accessed. 1 means it has been accessed, 0 means it has not been accessed, and it needs to be updated dynamically
public int[] already_arr;
//The precursor of each node. Each subscript represents the node, and the value corresponding to the subscript represents its precursor
public int[] pre_visited;
//Record the distance from the starting vertex to all other vertices. For example, if G is the starting vertex, record the distance from G to other vertices. It needs to be updated dynamically, and the calculated shortest distance will be stored in dis
public int[] dis;
/**
* constructor
* @param length Number of vertices
* @param index The starting vertex corresponds to the subscript, and the subscript of G vertex is 6
*/
public VisitedVertex(int length,int index){
this.already_arr = new int[length];
this.pre_visited = new int[length];
this.dis = new int[length];
//Initialize all distances to 65535, representing unreachable
Arrays.fill(dis,65535);
//The distance from the starting vertex to itself is initialized to 0
this.dis[index] = 0;
this.already_arr[index] = 1;//Mark that the current vertex has been accessed
}
/**
* Judge whether the index subscript vertex has been accessed
* @param index Vertex subscript
* @return Returns true if accessed, otherwise false
*/
public boolean isVisited(int index){
return already_arr[index] == 1;
}
/**
* Update the distance from the starting vertex to the index vertex
* @param index Starting point
* @param len Distance from departure vertex to index vertex
*/
public void updateDis(int index,int len){
dis[index] = len;
}
/**
* Update the index vertex precursor to the pre node (all operations are subscripts)
* @param index Subscript of current vertex
* @param pre The subscript of the precursor node to be updated
*/
public void updatePre(int index,int pre){
pre_visited[index] = pre;
}
/**
* Returns the distance from the starting vertex to the specified vertex
* @param index Specify vertex subscript
* @return
*/
public int getDis(int index){
return dis[index];
}
/**
* Continue to select and return to the new access vertex. For example, after G is accessed, A is used as the new access vertex (not the starting vertex)
* @return New access vertex subscript
*/
public int updateArr(){
int min = 65535,index = 0;//min represents the shortest path, initialized to 65535, and index represents the vertex subscript corresponding to the shortest path, initially 0
//Traverse the accessed node array, find the vertex with the shortest path and no access, and obtain the shortest path and the corresponding vertex subscript
for (int i = 0;i < already_arr.length;i++){
if(already_arr[i] == 0 && dis[i] < min){
min = dis[i];
index = i;
}
}
//Set the found vertex as visited
already_arr[index]=1;
return index;
}
/**
* Show final results
* Output three arrays
*/
public void show(){
System.out.println("============================");
for (int i : already_arr){
System.out.print(i + " ");
}
System.out.println();
for (int i : pre_visited){
System.out.print(i + " ");
}
System.out.println();
for (int i : dis){
System.out.print(i + " ");
}
System.out.println();
//In order to see the last shortest distance, we deal with it
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
int count = 0;
for (int i : dis) {
if (i != 65535) {
System.out.print(vertex[count] + "("+i+") ");
} else {
System.out.println("N ");
}
count++;
}
System.out.println();
}
}
























































