Time complexity and implementation of common sorting algorithms
Criteria for judging the advantages and disadvantages of sorting algorithm
Time complexity
The time complexity reflects the number of times a sorting algorithm executes in the sorting process, so the time complexity can be used to estimate the time speed of a sorting algorithm. The time complexity of common algorithms is O (1) < o (logn) < o (n) < o (nlogn) < o (N2)
Spatial complexity
Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during operation. It reflects the space occupation of a sorting algorithm.
Stability of sorting
It can ensure that two equal numbers, after sorting, remain in the same order before and after the sequence. (A1=A2, A1 before sorting is in front of A2, and A1 after sorting is still in front of A2).
Significance of stability
Stability is of little significance in numerical sorting alone. The essence of stability is to maintain the insertion order of data with the same attributes. If an object is sorted, because some attributes in the object contain special significance, it is necessary to place the objects with the same sorting attributes in the original relative position.
Summary of time complexity and space complexity of common algorithms
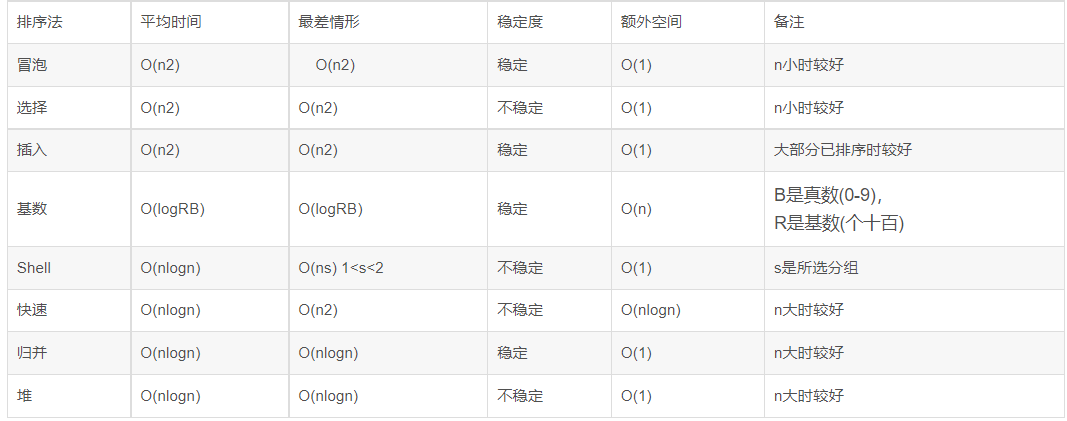
Stability classification:
Stable: bubble sort, insert sort, merge sort, cardinal sort
Unstable: select sort, quick sort, Hill sort, heap sort
Bubble sort
Thought:
From the left to the right, continue to turn the big elements back (or, from right to left, continue to move small elements forward). Comparison is a relatively adjacent two elements, and exchange occurs between the two elements. So, if the two elements are equal, there will be no exchange.
code implementation
public static void bubbleSort(int[] arrays){
boolean flag = true;
int temp = 0;
for (int i = 0; i < arrays.length - 1; i++) {
// Mutual exchange
for (int j = 0; j < arrays.length - 1 - i; j++) {
/** Big number to the back */
if (arrays[j] > arrays[j + 1]) {
flag = false;
temp = arrays[j];
arrays[j] = arrays[j + 1];
arrays[j + 1] = temp;
}
}
// If it is found that there is no exchange between elements after one exchange, it indicates that the array is ordered
if (flag) {
break;
} else {
// Reset tag,
flag = true;
}
}
}
Select sort
thought
Start from the first position and put the smallest of the remaining elements in the previous position each time.
code implementation
public static void selectSort(int[] arrays){
for (int i = 0; i < arrays.length; i++) {
//
int minIndex = i; // The smallest index, challenge arena method
for (int j = i + 1; j < arrays.length; j++) {
//
if (arrays[minIndex] > arrays[j]) {
// Pointer to the smallest element
minIndex = j;
}
}
// When the current element is the smallest element, no exchange occurs
if (minIndex != i) {
int temp = arrays[i];
arrays[i] = arrays[minIndex];
arrays[minIndex] = temp;
}
}
}
Insert sort
thought
Based on an ordered small sequence, insert one element at a time by comparing from right to left. At first, this small sequence had only one element. The comparison starts from the end of the ordered sequence. The element to be inserted is compared with the largest one that has been ordered. If it is larger than it, it is inserted directly behind it. Otherwise, it is compared continuously until it is smaller or equal to it, and then inserted behind it.
code implementation
/**
* Insert sort
* @param arrays Array to sort
*/
public static void insertSort(int[] arrays){
int insertValue = 0;
int insertIndex = 0;
for (int i = 1; i < arrays.length; i++) {
// Represents the value to insert
insertValue = arrays[i];
// Inserted index position
insertIndex = i;
// Conditional judgment: when the inserted element is smaller than the element before the insertion position, the element before the insertion position is moved back
while (insertIndex > 0 && arrays[insertIndex - 1] > insertValue) {
// Moves the previous position element back
arrays[insertIndex] = arrays[insertIndex - 1];
insertIndex--;
}
// Insert element
arrays[insertIndex] = insertValue;
}
}
Shell Sort
Thought:
Insert and sort the elements according to the asynchronous length. When the elements are disordered at the beginning, the step size is the largest, so the number of elements inserted and sorted is very small and the speed is very fast; When the elements are basically ordered and the step size is very small, insertion sorting is very efficient for ordered sequences. Therefore, the time complexity of Hill sort will be better than o(n^2). Due to multiple insertion sorting, we know that one insertion sorting is stable and will not change the relative order of the same elements. However, in different insertion sorting processes, the same elements may move in their respective insertion sorting, and finally their stability will be disturbed. Therefore, shell sorting is unstable. The elements are grouped, and each group is inserted and sorted.
code implementation
public static void shellSort(int[] arr) {
// The number of grouping sorting, gap is the step size
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
// Insert and sort each group of the group
for (int i = gap; i < arr.length; i++) {
// Insertion position
int index = i;
// insert values
int value = arr[i];
// Insert only when the current insert value is less than the previous position
if (arr[i] < arr[i - gap]) {
while (index - gap >= 0 && value < arr[index - gap]) {
arr[index] = arr[index - gap];
index -= gap;
}
// Insert value
arr[index]=value;
}
}
}
}
Single axis quick sort
thought
Select an element in the array as the axis, partition the array, put the elements larger than the axis on the right and the small elements on the left, and then quickly sort the left and right. Therefore, this is a recursive process.
code implementation
public static void quickSort(int[] array, int leftBound, int rightBound) {
if (leftBound >= rightBound) {
return;
}
//First partition
int mid = partition(array, leftBound, rightBound);
// Sort left
quickSort(array, leftBound, mid - 1);
// Sort right
quickSort(array, mid + 1, rightBound);
}
/**
* Zone return to center axis position
*
* @param array
* @param leftBound Partition left boundary
* @param rightBound Partition has boundary
* @return Returns the position of the axis
*/
public static int partition(int[] array, int leftBound, int rightBound) {
// Select the last element as the axis
int pivot = array[rightBound];
int left = leftBound;
int right = rightBound - 1;
while (left <= right) {
while (left <= right && array[left] <= pivot) left++;
while (left <= right && array[right] > pivot) right--;
if (left < right) {
// Exchange the on both sides of the shaft
swap(array, left, right);
}
}
swap(array, left, rightBound);
return left;
}
/**
* Left-right exchange
*
* @param array
* @param l
* @param r
*/
public static void swap(int[] array, int l, int r) {
int temp = array[l];
array[l] = array[r];
array[r] = temp;
}
Merge sort
thought
Merging is the idea of divide and conquer. The sequence is recursively divided into short sequences. The recursive exit is that the short sequence has only one element (it is considered as direct order at this time) or two sequences (one comparison and exchange), and then each ordered short sequence is combined into an ordered long sequence, which is continuously combined until all the original sequences are in order.
code implementation
/**
* * Merge sort
*
* @param arr
* @param leftBound Left boundary
* @param rightBound There are boundaries
*/
public static void sort(int[] arr, int leftBound, int rightBound) {
// There is only one element
if (leftBound == rightBound) {
return;
}
if (leftBound > rightBound || leftBound < 0 || rightBound < 0) {
throw new RuntimeException("Boundary anomaly");
}
// Middle separation
int mid = leftBound + (rightBound - leftBound) / 2;
// Sort left
sort(arr, leftBound, mid);
// Sort right
sort(arr, mid + 1, rightBound);
// Merger,
merge(arr, leftBound, mid + 1, rightBound);
}
/**
* Merge two arrays
*
* <p>Default from small to large
*
* @param arr Sorted array
* @param leftPtr Left pointer
* @param rightPtr Right pointer
* @param rightBound Right boundary
*/
public static void merge(int[] arr, int leftPtr, int rightPtr, int rightBound) {
// Temporary auxiliary array to store the merged array
int[] temp = new int[rightBound - leftPtr + 1];
int i = leftPtr;
int j = rightPtr;
int k = 0;
while (i < rightPtr && j <= rightBound) {
temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
}
//Among them, there are left about
while (i < rightPtr) temp[k++] = arr[i++];
while (j <= rightBound) temp[k++] = arr[j++];
for (int m = 0; m < temp.length; m++) {
arr[leftPtr + m] = temp[m];
}
}
Cardinality sort
thought
Cardinality sorting is sorting according to the low order, and then collecting; Then sort according to the high order, and then collect; And so on until the highest order. Sometimes, some attributes have priority order. They are sorted by low priority first, and then by high priority. The last order is that the high priority comes first, and the low priority with the same high priority comes first.
public static void radixSort(int[] arr) {
/** Get digits */
int digit = arrMaxDigit(arr);
/** Array of counts */
int[] count = new int[10];
/** Store the results of one sorting */
int[] result = new int[arr.length];
/** Each cycle is a count sort */
for (int i = 0; i < digit; i++) {
/** Number of bits removed */
int div = (int) Math.pow(10, i);
for (int j = 0; j < arr.length; j++) {
/** The value of each bit is bits - > tens - > hundreds */
count[arr[j] / div % 10]++;
}
for (int m = 1; m < count.length; m++) {
count[m] = count[m - 1] + count[m];
}
/** Sort restore array */
for (int k = arr.length - 1; k >= 0; k--) {
result[--count[arr[k] / div % 10]] = arr[k];
}
System.arraycopy(result, 0, arr, 0, result.length);
/** Reset count array */
Arrays.fill(count, 0);
}
}
/**
* * Returns the maximum number of bits in the array
*
* @param arr
* @return
*/
private static int arrMaxDigit(int[] arr) {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
return (max + "").length();
}