Sort:
1. Sorting is often encountered in computer data processing. In daily data processing, it is generally believed that 1/4 of the time is spent on sorting, while for program installation.
Up to 50% of the time is spent sorting tables. In short, sorting is the ordering of a random set of data in a regular order.
2. Inline and Outline: According to the sorting method in the sorting process whether the data elements are completely in memory and divided, if part of the data is out of memory, it is out, otherwise, it is inside.
3. Stability of sorting algorithm: It depends on whether the order of the same elements will change after sorting.
If two numbers a and b, a = B and a is in front of b, if a is still in front of B after sorting, then it is stable, otherwise, it is unstable.
4. Performance evaluation of sorting algorithm: The execution time of the algorithm is the most important parameter to measure the performance of the algorithm, and its time cost can be measured by the number of data comparisons and mobile times in the execution of the algorithm.
Sorting algorithm:
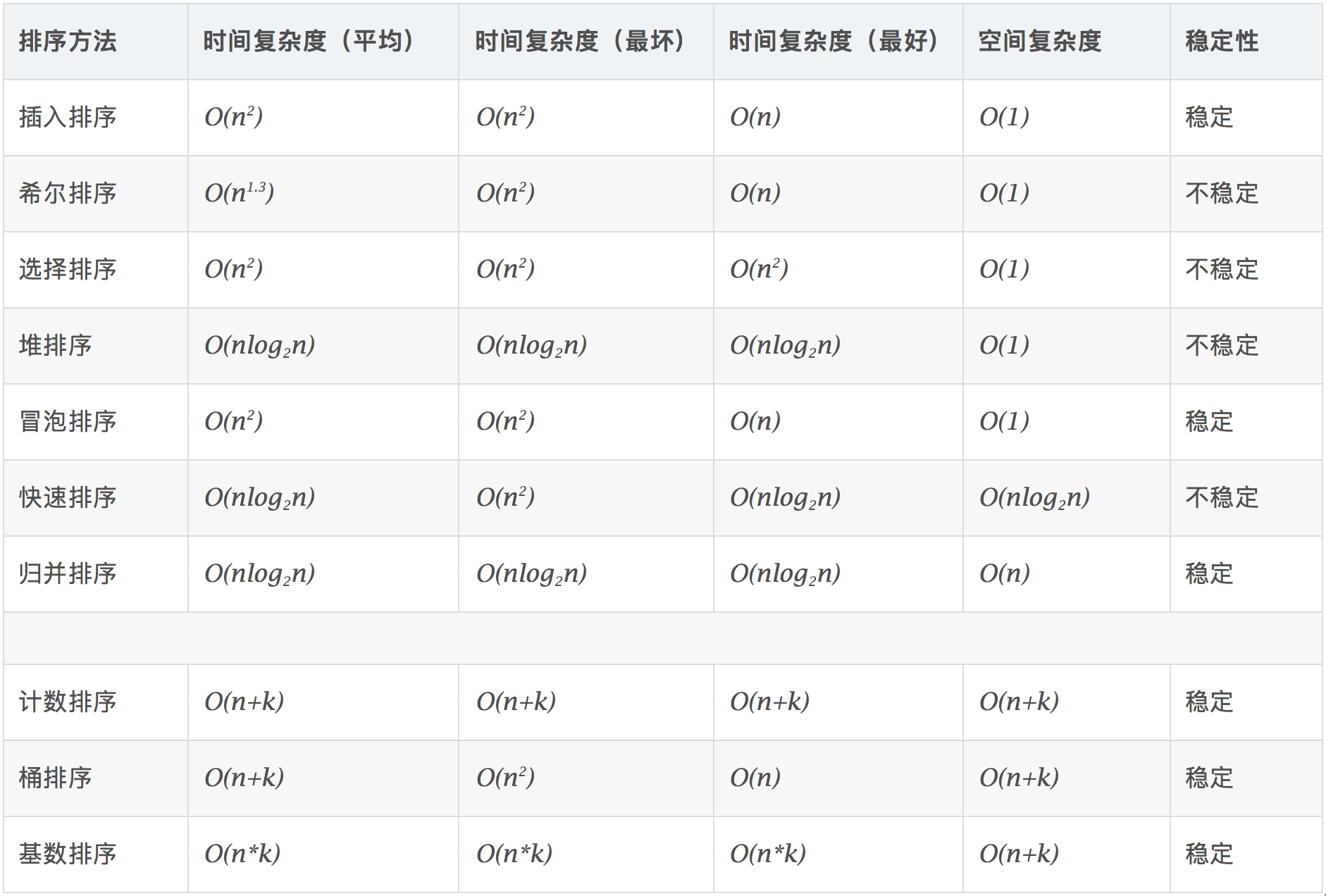
1. Time complexity:
a, Square Order (O(n2)) Sorting Various Simple Sorting: Direct Insertion, Direct Selection and Bubble Sorting
(b) Linear logarithmic order (O (nlog2n) sorting: quick sorting, heap sorting and merge sorting
c, O(n1+) sort, is a constant between 0 and 1: Hill sort
d, Linear Order (O(n)) Sorting: Cardinal Sorting, Bucket Sorting and Number Sorting
2. Stability:
a. Stable sorting algorithms: bubble sorting, insert sorting, merge sorting, count sorting, bucket sorting and cardinal sorting
b. Unstable sorting algorithms: Selective sorting, Quick sorting, Hill sorting, heap sorting
Note: Stability is relative. For example, if we change the algorithm of comparing two elements in bubble sort to greater than or equal to, it will become unstable!
3. Comparisons and non-comparisons:
a. Comparing Sorting: Bubble Sorting, Insert Sorting, Hill Sorting, Selection Sorting, Quick Sorting, Merge Sorting and Heap Sorting
b. Non-comparative Sorting: Count Sorting, Bucket Sorting and Base Sorting
Top Ten Classical Sorting Algorithms:
The following are sorted in non-descending order
1. Bubble Sort:
(a) Compare two adjacent elements, and if the former is larger than the latter, exchange the two elements.
b. Move one item backwards and perform a comparison exchange operation; when moved to the last bit, this element is the maximum value of this round.
c. Start from scratch, except for the last one, perform a and b operations until the sorting is complete
Note: In the sorting process, we can set a flag to determine whether there are exchange elements in a round sorting. If there is no exchange after a round sorting, the sorting is completed.
#include <iostream> #include <vector> #include <cstdlib> //Reference is used, otherwise only a parameter that does not change the original data is passed in. void bubbleSort(std::vector<int>& nums); int main() { std::vector<int> nums; int len = 0; std::cout<<"Please enter the length:"; do { std::cin>>len; if (len <= 0) // Standard error stream, output error message std::cerr<<"Please enter a positive integer:"; } while (len <= 0); int num = 0; std::cout<<"input "<<len<<" Number: "; // size_t yes unsigned_int Type. It is recommended to use subscripts, but if a negative number is assigned to it, it will be converted to a positive number, resulting in errors. for (size_t i = 0; i < len; ++i) { std::cin>>num; nums.push_back(num); } bubbleSort(nums); std::cout<<"The sorted array:"; // free for loop for (int num : nums) // std::ends Output blank characters, different computers may have different blank characters std::cout<<num<<std::ends; std::cout<<std::endl; system("pause"); return 0; } void bubbleSort(std::vector<int>& nums) { // Set a swap flag. If all elements do not swap after a loop, the array is arranged and can exit in advance. bool exchange = false; size_t len = nums.size(); for (size_t i = 1; i < len; ++i) { exchange = false; // For convenience, I moved the smallest element to the front. for (size_t j = len-1; j >= i; j--) { if (nums[j-1] > nums[j]) { int temp = nums[j-1]; nums[j-1] = nums[j]; nums[j] = temp; exchange = true; } } if (!exchange) return; } }
2. Selection Sort:
(a) Find the smallest element i n the initial sequence R[i...n-1] and place it at R[i], i=0, n = the size of the object to be arranged
b,++i
c. Repeat operation a and b until round n-1
void selectionSort(std::vector<int>& nums) { size_t len = nums.size(); // Choose the smallest one at the top of each cycle for (size_t i = 0; i < len-1; ++i){ int min = i; for (size_t j = i+1; j < len; ++j){ if (nums[j] < nums[min]) min = j; } if (i != min){ int temp = nums[i]; nums[i] = nums[min]; nums[min] = temp; } } return ; }
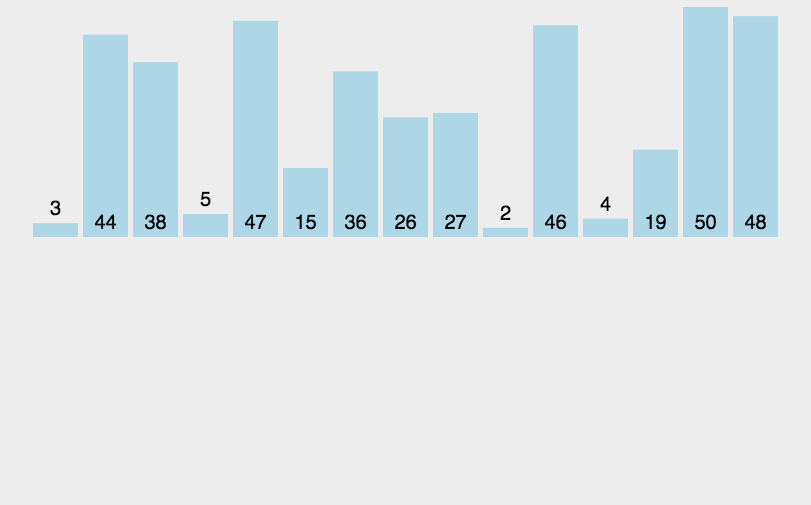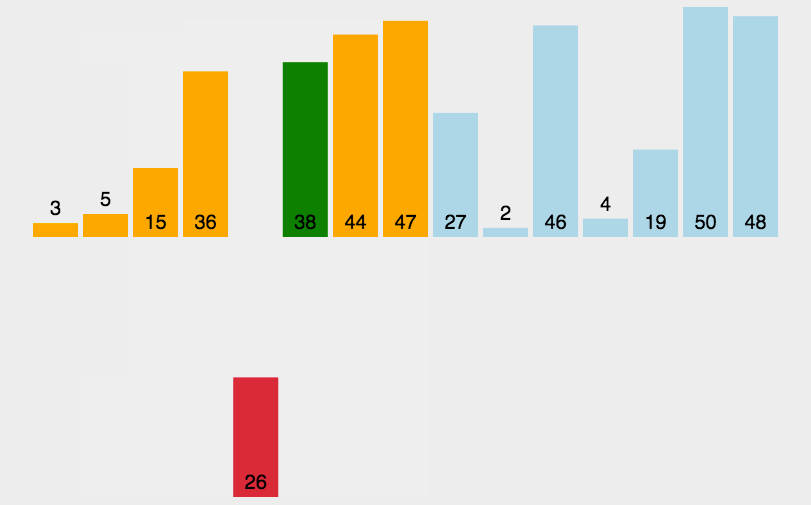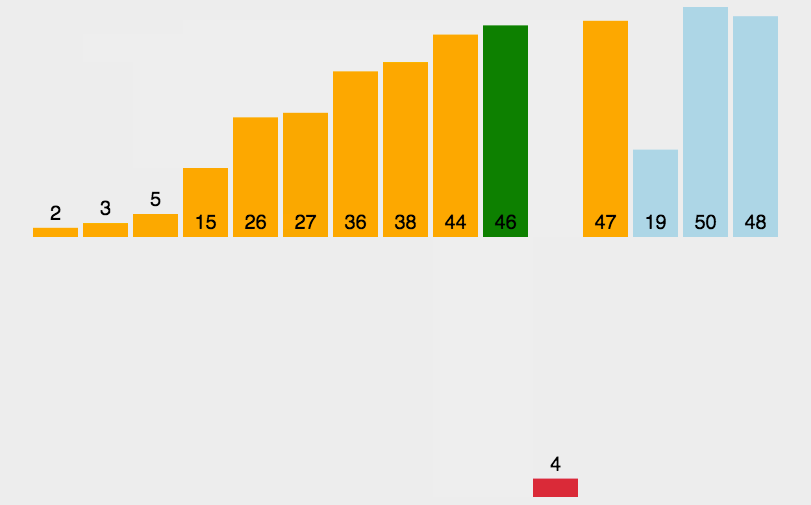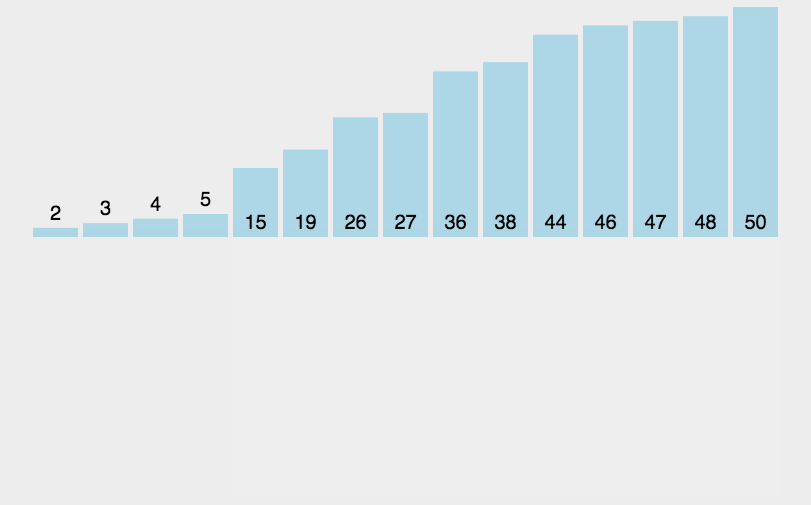
3. Insertion Sort:
a. Starting with the first element, the element can be considered sorted
b. Take out the next element and scan backwards and forwards in the ordered sequence of elements
c. If the element is larger than the new element, move the element to the next location
d, repeat operation c until the sorted element is found to be less than or equal to the new element
e. After inserting a new element into that location
f. Repeated operation b-e
void insertionSort(std::vector<int>& nums) { size_t len = nums.size(); for (size_t i = 1; i < len; i++) { int temp = nums[i]; // Move the larger number one bit back in the loop size_t j = i; while (j > 0 && temp < nums[j-1]) { nums[j] = nums[j-1]; j--; } if (j != i) nums[j] = temp; } return ; }
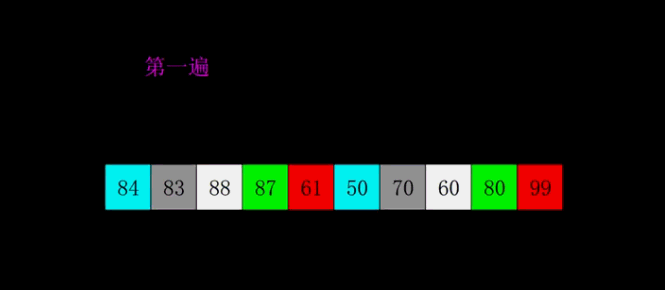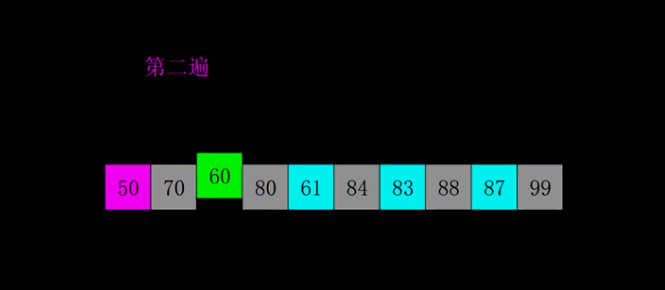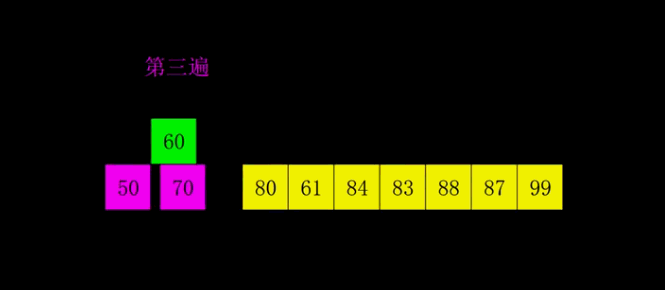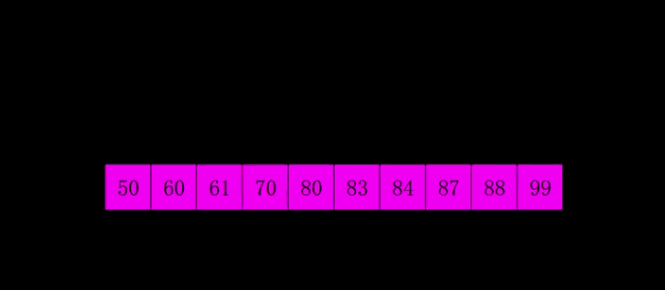
4. Shell Sort:
(a) Assuming that the object has n elements, the integer gap < n is taken as the interval, and all elements are divided into gap subsequences. All elements whose distances are gap are placed in the same subsequence.
Direct insertion sorting is performed in each subsequence
b. Reduce the gap, such as gap = gap/3+1
c, repeat operations a and b until gap = 1 is taken as
Note: There are many choices for gap, but if gap = n/2 or gap = gap/2, only the odd position at the last step can be compared with the even position.
void shellSort(std::vector<int>& nums) { int gap = 1, len = nums.size(); // First let interval gap As big as possible while (gap < len) gap = gap*3+1; while (gap > 0){ for (int i = gap; i < len; i++){ int temp = nums[i]; int j = i - gap; // Direct insertion sort while (j >= 0 && nums[j] > temp){ nums[j+gap] = nums[j]; j -= gap; } nums[j+gap] = temp; } gap /= 3; } return ; }
Quick Sort:
A. Select an element from a sequence, called a "benchmark" (usually the first element)
b. Rearrange the sequence. All elements smaller than the base value are placed in front of the base, and all elements larger than the base value are placed behind the base (the same number can reach either side).
After the partition exits, the benchmark is in the middle of the sequence. This is called partition operation.
c. Recursively rank subordinate columns smaller than the base value element and larger than the base value element
Note: Fast-paced non-recursive algorithms can be implemented using stacks
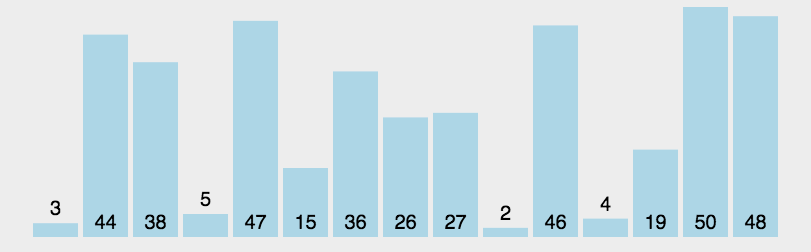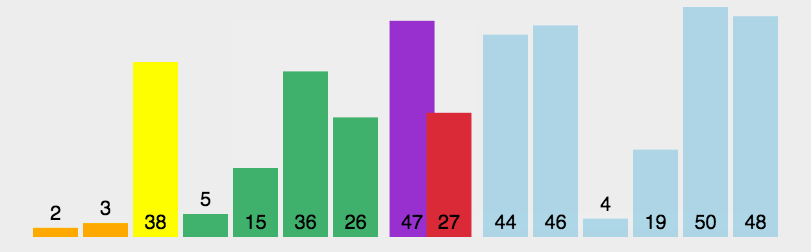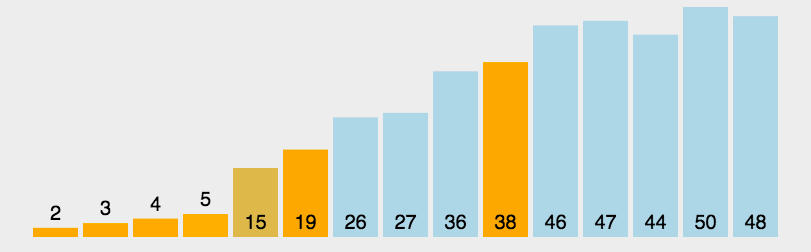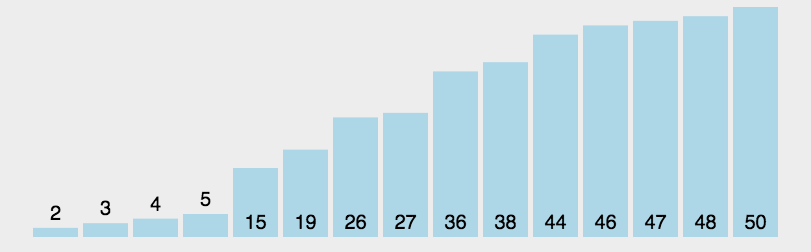
void quickSort(int* arr, int low, int high) { int star = low, end = high; if (star > end) return ; int temp = arr[star]; while (star != end) { // Find the number less than the "benchmark" from now on while (arr[end] >= temp && star < end) end--; // In the past, we found a number larger than the "benchmark" while (arr[star] <= temp && star < end) star++; // If it's still within the scope, exchange the two. if (star < end) { int t = arr[star]; arr[star] = arr[end]; arr[end] = arr[star]; } } // Move "benchmark" to "middle" int t = arr[low]; arr[low] = arr[star]; arr[star] = t; // recursion quickSort(arr, low, star-1); quickSort(arr, star+1, high); return ; }