The core class of the Executor framework is ThreadPoolExecutor, which is the implementation class of the thread pool. See ThreadPoolExecutor Source Parsing .Executors also provides us with four common thread pools, all based on ThreadPoolExecutor and one based on ForkJoinPool.

FixedThreadPool

Usage

ExecutorService fixedThreadPool = Executors.newFixedThreadPool(10);

Create a thread pool with 10 worker threads.

Realization

public static ExecutorService newFixedThreadPool(int nThreads) {
	return new ThreadPoolExecutor(nThreads, nThreads,
								  0L, TimeUnit.MILLISECONDS,
								  new LinkedBlockingQueue<Runnable>());
}

We can see:

• It actually creates a ThreadPoolExecutor where the number of core threads (corePoolSize) and the maximum number of threads (maximumPoolSize) are both nThreads
• keepAliveTime of 0 means that the thread will be recycled as soon as it is idle
• It uses the LinkedBlockingQueue queue to store tasks, but the default length of the queue is Integer.MAX_VALUE, which can cause memory overflow when there are too many tasks, so it is not recommended.

Running Diagram

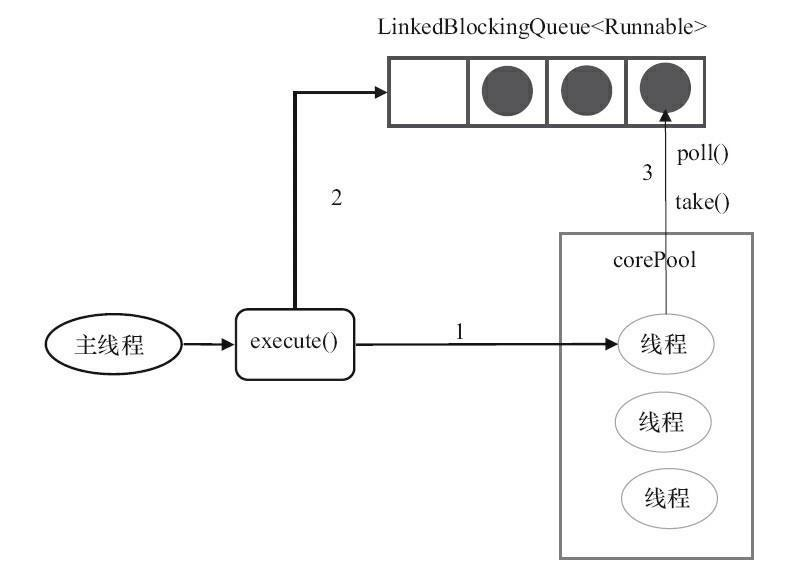
SingleThreadExecutor

Usage

ExecutorService singleThreadExecutor = Executors.newSingleThreadExecutor();

Create a thread pool with 1 worker threads.

Realization

public static ExecutorService newSingleThreadExecutor() {
	return new FinalizableDelegatedExecutorService
		(new ThreadPoolExecutor(1, 1,
								0L, TimeUnit.MILLISECONDS,
								new LinkedBlockingQueue<Runnable>()));
}

We can see:

• It actually creates a ThreadPoolExecutor with a core number of threads (corePoolSize) and a maximum number of threads (maximumPoolSize) of 1
• keepAliveTime of 0 means that the thread will be recycled as soon as it is idle
• It also uses the LinkedBlockingQueue queue to store tasks, but the default length of the queue is Integer.MAX_VALUE, which can cause memory overflow when there are too many tasks, so it is not recommended.

Running Diagram

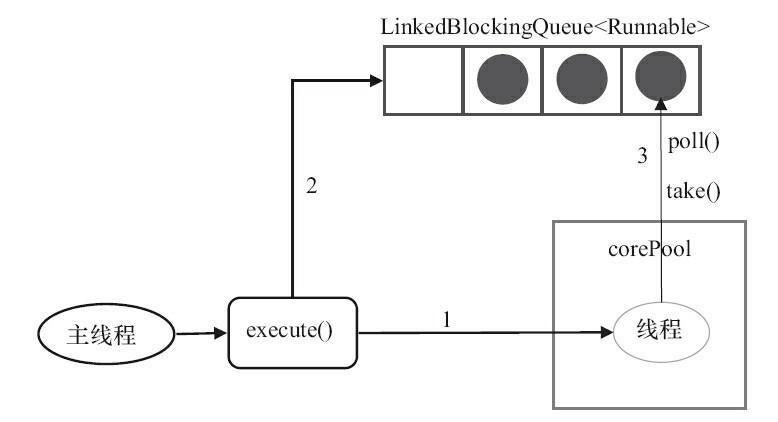
CachedThreadPool

Usage

ExecutorService cachedThreadPool = Executors.newCachedThreadPool();

Create a thread pool where the maximum number of worker threads is Integer.MAX_VALUE.

Realization

public static ExecutorService newCachedThreadPool() {
	return new ThreadPoolExecutor(0, Integer.MAX_VALUE,
								  60L, TimeUnit.SECONDS,
								  new SynchronousQueue<Runnable>());
}

We can see:

• The number of threads created in a core pool (corePoolSize) is 0 and the maximum number of threads (maximumPoolSize) is ThreadPoolExecutor for Integer.MAX_VALUE. The number of threads in this pool is uncontrollable and in extreme cases may exhaust CPU and memory resources by creating too many threads, which is not recommended.
• Idle threads last 1 minute
• It also uses a SynchronousQueue queue to store tasks, which by default does not store elements, and each put operation must wait for a take operation, otherwise elements cannot be added.Change Thread Pool continuously adds new worker threads to execute tasks when there are always task submissions

Running Diagram

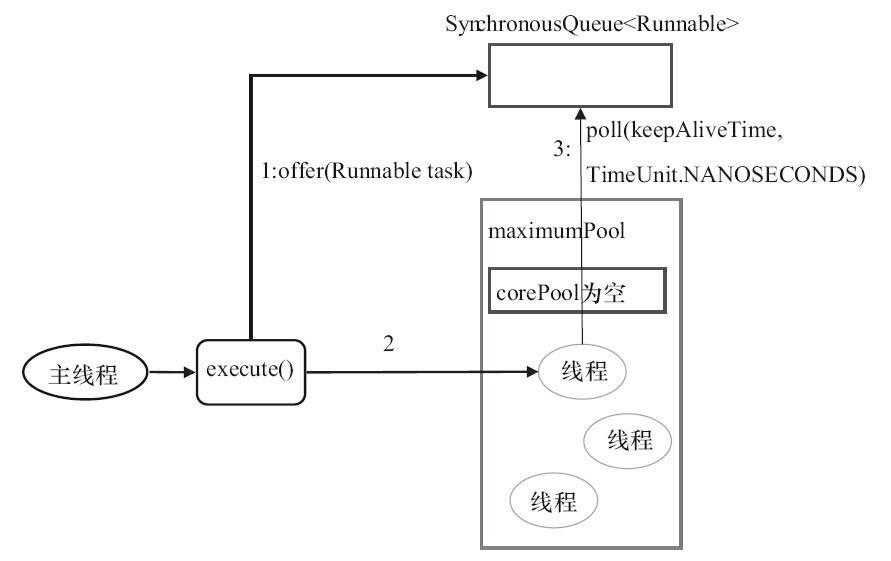
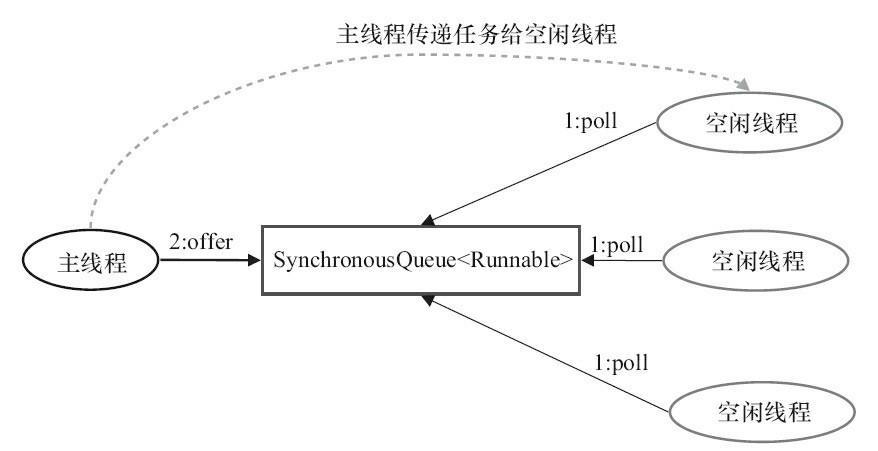
As mentioned earlier, SynchronousQueue is a blocked queue with no capacity.Each insert operation must wait for a corresponding removal from another thread, and vice versa.CachedThreadPool uses SynchronousQueue to pass tasks submitted by the main thread to the idle thread for execution.A diagram of task delivery in CachedThreadPool is shown below:

ScheduledThreadPoolExecutor

ScheduledThreadPoolExecutor inherits from ThreadPoolExecutor.It is primarily used to run tasks after a given delay or to perform tasks on a regular basis.ScheduledThreadPoolExecutor has functionality similar to Timer, but ScheduledThreadPoolExecutor is more powerful and flexible.

Usage

ScheduledExecutorService scheduledThreadPool = Executors.newScheduledThreadPool(10);

scheduledThreadPool.scheduleAtFixedRate(() -> {
    System.out.println(Thread.currentThread().getName() + "   " + LocalDateTime.now().format(DateTimeFormatter.ISO_LOCAL_DATE_TIME));
    //0 is the delay time for the first execution of a task, 1 is the interval between each execution of a task, TimeUnit.SECONDS is the interval value unit
}, 0, 1, TimeUnit.SECONDS);

When a core thread is created, 10, the maximum number of worker threads is the thread pool of Integer.MAX_VALUE.

Run result:

Connected to the target VM, address: '127.0.0.1:50560', transport: 'socket'
pool-4-thread-1   2019-08-06T15:57:08.942
pool-4-thread-1   2019-08-06T15:57:09.802
pool-4-thread-2   2019-08-06T15:57:10.803
pool-4-thread-1   2019-08-06T15:57:11.803
pool-4-thread-3   2019-08-06T15:57:12.803
pool-4-thread-2   2019-08-06T15:57:13.803

Realization

public static ScheduledExecutorService newScheduledThreadPool(int corePoolSize) {
	return new ScheduledThreadPoolExecutor(corePoolSize);
}

public ScheduledThreadPoolExecutor(int corePoolSize) {
	super(corePoolSize, Integer.MAX_VALUE, 0, NANOSECONDS,
		  new DelayedWorkQueue());
}

We can see:

• The number of threads created in a core pool (corePoolSize) is 10 and the maximum number of threads (maximumPoolSize) is ThreadPoolExecutor for Integer.MAX_VALUE. The number of threads in this pool is uncontrollable and in extreme cases may exhaust CPU and memory resources by creating too many threads, which is not recommended.
• Idle threads have a lifetime of 0 and are recycled once idle
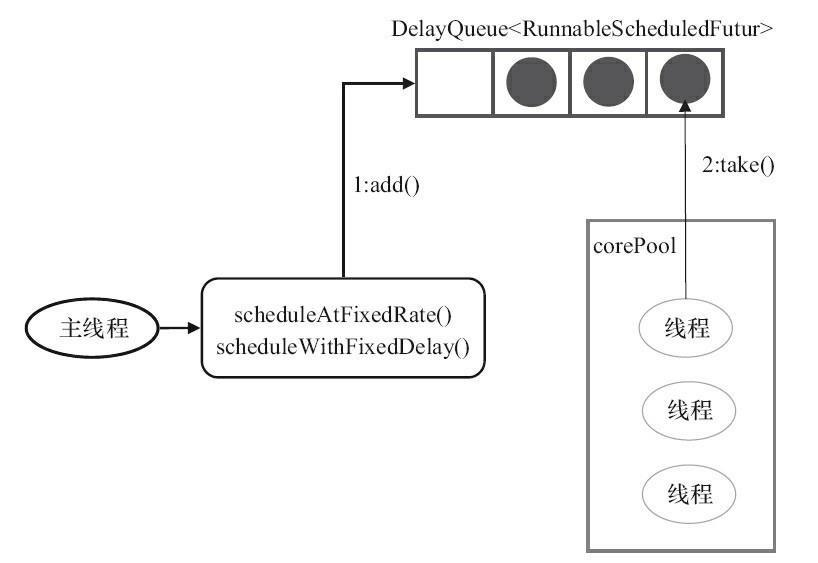
• It also uses the DelayedWorkQueue queue to store tasks, which is a delayed queue that can only store RunnableScheduledFuture tasks, and we generally use its subclass ScheduledFutureTask.

ScheduledFutureTask Class Diagram

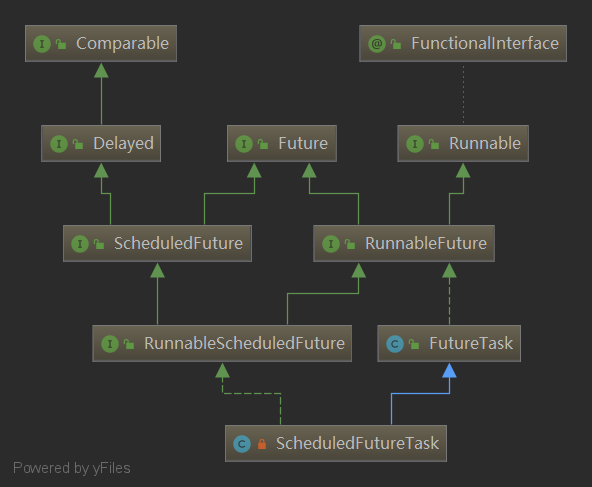
ScheduledFutureTask Core Properties

/** Represents the serial number that this task was added to ScheduledThreadPoolExecutor */
private final long sequenceNumber;

/** Indicates when the task will be executed */
private long time;

/** Represents the interval period between task executions */
private final long period;

Running Diagram

WorkStealingPool

Usage

ExecutorService workStealingPool = Executors.newWorkStealingPool();

Create a ForkJoinPool thread pool whose default size is the number of CPU cores.

Realization

public static ExecutorService newWorkStealingPool() {
	return new ForkJoinPool
		(Runtime.getRuntime().availableProcessors(),
		 ForkJoinPool.defaultForkJoinWorkerThreadFactory,
		 null, true);
}

We can see:

• It actually creates a ForkJoinPool where the number of core threads is the number of CPU cores

summary

As we can see from the above, most thread pools are not recommended for direct use. We try to use ThreadPoolExecutor to create them when using thread pools and set the values of corePoolSize, maximumPoolSize, keepAliveTime, BlockingQueue, RejectedExecutionHandler according to business reasons, otherwise OnlineThe upper environment can easily exhaust CPU and memory resources, rendering services unavailable.

Reference resources

Art of java Concurrent Programming

Source code

https://github.com/wyh-spring-ecosystem-student/spring-boot-student/tree/releases

spring-boot-student-concurrent project

layering-cache

Laying-cache, a multilevel caching framework for monitoring This is an implementation of my open source multilevel caching framework. If you are interested, you can see