1, Foreword
It refers to the division of similar data together. The specific division does not care about this kind of label. The goal is to aggregate similar data together. Clustering is an unsupervised learning method.
2, General process of clustering
- Data preparation: feature standardization and dimensionality reduction
- Feature selection: select the most effective feature from the original feature and store it in the vector
- Feature extraction: transform the selected features to form new prominent features
- Clustering: measure the similarity based on a certain distance function to obtain clusters
- Evaluation of clustering results: analyze clustering results, such as distance error sum (SSE), etc
3, Data clustering method
Data clustering methods can be divided into partition based methods, density based methods and hierarchical methods.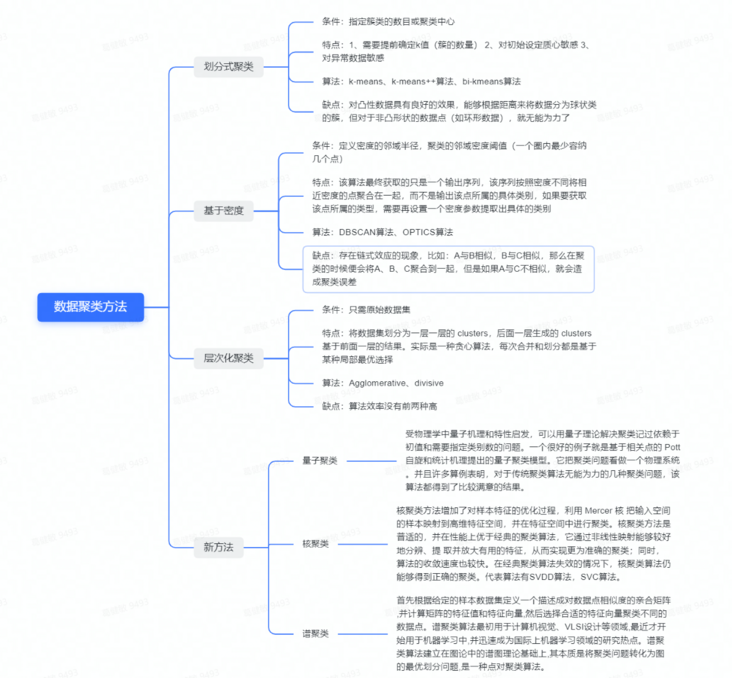
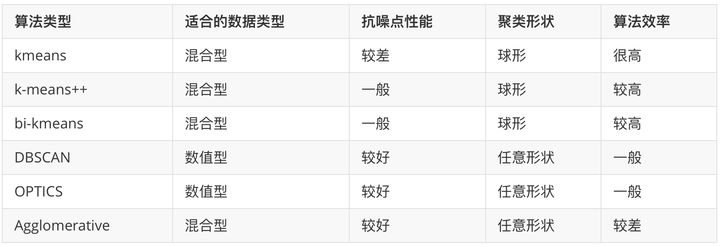
4, Criteria for measuring clustering algorithms
Different clustering algorithms have different advantages and disadvantages and different application conditions. Generally speaking, it can be seen from the attributes of data (whether sequence input, dimension), the preset of algorithm model and the processing capacity of the model. The details are as follows:
1. Algorithm processing capacity: the ability to process large data sets (i.e. algorithm complexity); Ability to deal with data noise; The ability to handle arbitrary shapes, including nested data with gaps;
2. Whether the algorithm needs preset conditions: whether the number of clusters needs to be known in advance and whether the user needs to give domain knowledge;
3. Data input attribute of algorithm: whether the result of algorithm processing is related to the order of data input, that is, whether the algorithm is independent of the order of data input; The algorithm has the ability to process many attribute data, that is, whether it is sensitive to the dimension of data and whether it has requirements for the type of data.
5, Algorithm implementation
#k-means++
class KMeansClusterAlgorithm(object):
'''
this class is k-means cluster algorithm
Author:
xxx
Date:
2022-02-10
'''
def __init__(self, dataset: list, k: int) -> None:
'''
initial Args
Args:
dataset:list. like [[x1,y1],[x2,y2)]
k:int. number of cluster what to get
'''
self.dataset = dataset
self.k = k
def point_avg(self, points) -> list:
'''
Accepts a list of points, each with the same number of dimensions.
NB. points can have more dimensions than 2
Returns a new points which is the center of all the points
Args:
points:list. a list of points, like [[x,y],[x1,y1],[x2,y2]]
Return:
new_center: list
'''
dimensions = len(points[0])
new_center = []
for dimension in range(dimensions):
dim_sum = 0
for p in points:
dim_sum += p[dimension]
# average of each dimension
new_center.append(dim_sum/float(len(points)))
return new_center
# def update_centers(self, date_set, assignments):
def update_centers(self, assignments) -> list:
'''
Accepts a dataset and a list of assignments; the indexes of both lists correspond
to each other.
compute the center for each of the assigned groups.
Reture 'k' centers where is the number of unique assignments.
Args:
dataset:
assignments:
Return:
centers:list ex:[[1,2]]
'''
new_means = defaultdict(list)
centers = []
for assigment, point in zip(assignments, self.dataset):
new_means[assigment].append(point)
for points in new_means.values():
centers.append(self.point_avg(points))
return centers
def distance(self, a: list, b: list) -> int:
'''
caculate two points' distance
Args:
a:list. point a,ex:[1,3]
b:list. point b,ex:[1,3]
Return:
:int: the distance of two point
'''
dimensions = len(a)
_sum = 0
for dimension in range(dimensions):
difference_seq = (a[dimension] - b[dimension]) ** 2
_sum += difference_seq
return sqrt(_sum)
def _assign_points(self, centers) -> list:
'''
assign each point to an index that corresponds to the index
of the center point on its proximity to that point.
Return a an array of indexes of the centers that correspond to
an index in the data set; that is, if there are N points in data set
the list we return will have N elements. Also If there ara Y points in centers
there will be Y unique possible values within the returned list.
Args:
data_points:list ex:[[1,2],[3,4],[5,6]]
centers:list ex:[[3,4]]
Return:
assigments:list
'''
assigments = []
for point in self.dataset:
shortest = float('Inf')
shortest_index = 0
for i in range(len(centers)):
val = self.distance(point, centers[i])
if val < shortest:
shortest = val
shortest_index = i
assigments.append(shortest_index)
return assigments
# def generate_k(self, data_set: list, k: int, centers: list = []) -> list:
def _generate_k(self, centers: list = []) -> list:
'''
Given data set, which is an list of lists,
find the minimum and maximum for each coordinate,a range.
Generate k random points between the ranges.
Return a list of the random points within the ranges
use self.dataset self.k
Args:
data_set:list. ex:[[1,2],[3,4]]
k:int. the number of clusters
Return:
list ex:[[1,2]]
'''
# centers = []
dimensions = len(self.dataset[0])
min_max = defaultdict(int)
for point in self.dataset:
for i in range(dimensions):
val = point[i]
min_key = f'min_{i}'
max_key = f'max_{i}'
if min_key not in min_max or val < min_max[min_key]:
min_max[min_key] = val
if max_key not in min_max or val > min_max[max_key]:
min_max[max_key] = val
for _k in range(self.k):
rand_point = []
for i in range(dimensions):
min_val = min_max[f'min_{i}']
max_val = min_max[f'max_{i}']
rand_point.append(uniform(min_val, max_val))
centers.append(rand_point)
return centers
def _euler_distance(self, point1: list, point2: list) -> float:
'''
Calculate euler distance between two points, support multidimensional
Args:
point1:list
point2:list
Return:
:float
'''
distance = 0.0
for a, b in zip(point1, point2):
distance += math.pow(a - b, 2)
return math.sqrt(distance)
def get_closest_dist(self, point, centroids) -> float:
'''
get closest dist between two point
Args:
point1:list
centroids:list. the center of cluster
Return:
min_dist:float
'''
min_dist = math.inf # Initial set to infinity
for i, centroid in enumerate(centroids):
dist = self._euler_distance(centroid, point)
if dist < min_dist:
min_dist = dist
return min_dist
def _kpp_centers(self) -> list:
'''
calculate cluster center
use self.dataset and self.k
Return:
cluster_centers:list. self.k(the number of cluster center that user defined) cluster center
'''
cluster_centers = []
cluster_centers.append(random.choice(self.dataset))
d = [0 for _ in range(len(self.dataset))]
for _ in range(1, self.k):
total = 0.0
for i, point in enumerate(self.dataset):
# The distance from the nearest cluster center
d[i] = self.get_closest_dist(point, cluster_centers)
total += d[i]
total *= random.random()
# The next clustering center is selected by wheel method.
for i, di in enumerate(d):
total -= di
if total > 0:
continue
cluster_centers.append(self.dataset[i])
break
return cluster_centers
# def k_means(self, dataset:list, k:int):
def k_means_plusplus(self) -> tuple:
'''
the enter of k-means cluster algorithm
Args:
data_set:list. ex:[[1,2],[3,4]]
k:int. the number of clusters
Return:
(assignments, self.dataset):tuple (result list,origin datalist)
'''
# k_points = self._generate_k() #[[1,2],[3,4]]
k_points = self._kpp_centers()
assignments = self._assign_points(k_points) # [1,2,1,1,0,0,4]
old_assignments = None
times = 0
while assignments != old_assignments:
new_centers = self.update_centers(assignments) # [[11.2],[12.2]]
old_assignments = assignments
assignments = self._assign_points(new_centers)
return (assignments, self.dataset)
reference material
https://zhuanlan.zhihu.com/p/...
https://blog.csdn.net/abc2009...
https://blog.csdn.net/weixin_...
https://www.cnblogs.com/wang2...