On the first day of 2022, tiger, tiger, I wish you a happy year of the tiger!!! Here comes the first blog of the year
catalogue
3.1 override equal of base class
3.2 comparison based on Comparble interface classes
3.3 comparator based comparison
3.4 comparison of three methods
6. Problems left over from last class
1. Questions raised
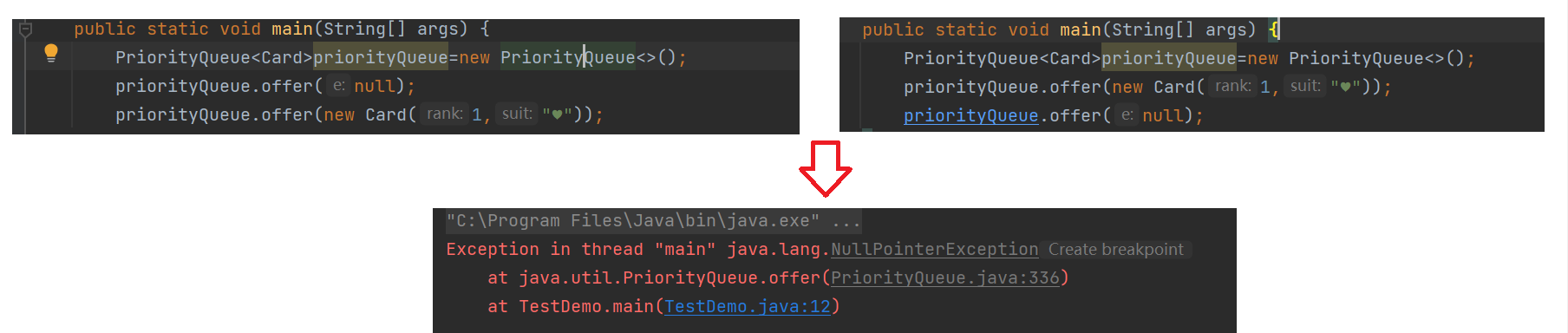
2. Comparison of elements
2.1 comparison of basic types
public class TestCompare {
public static void main(String[] args) {
//① Comparison of integer data
int a = 10; int b = 20;
System.out.println(a > b);
System.out.println(a < b);
System.out.println(a == b);
//② Comparison of character data
char c1 = 'A';
char c2 = 'B';
System.out.println(c1 > c2);
System.out.println(c1 < c2);
System.out.println(c1 == c2);
//Comparison of Boolean data
boolean b1 = true;
boolean b2 = false;
System.out.println(b1 == b2);
System.out.println(b1 != b2); } }2.2 comparison of objects
class Card {
public int rank;
// Value public String suit;
// Decor public Card(int rank, String suit){
this.rank = rank;
this.suit = suit;
}
}
public class TestPriorityQueue {
public static void main(String[] args) {
Card c1 = new Card(1, "♠");
Card c2 = new Card(2, "♠");
Card c3 = c1;
System.out.println(c1 > c2);
// Compilation error
System.out.println(c1 == c2);
// Compilation succeeded ---- > Print false because c1 and c2 point to different objects
System.out.println(c1 < c2); // Compilation error
System.out.println(c1 == c3); // Compilation succeeded ----- > Print true because c1 and c3 point to the same object
}
}3. Comparison of objects
In some cases, the contents of objects need to be compared. For example, when inserting an object into the priority queue, the heap needs to be adjusted according to the contents of the object. What should be done?
3.1 override equal of base class
Note: when you want to compare whether two custom types are the same and have the same content, you must override its equals method

The modification code is:
class Card{
public int rank;
public String suit;
public Card(int rank, String suit) {
this.rank = rank;
this.suit = suit;
}
@Override
public String toString() {
return "Card{" +
"rank=" + rank +
", suit='" + suit + '\'' +
'}';
}
@Override
public boolean equals(Object o) {
//If this and o refer to the same object
if (this == o) return true;
//getClass () compares the same type here. If not, false will be returned; Of course, instanceof can be used here to judge
//If (o = = null | (o instanceof card)) can be replaced by this sentence
if (o == null || getClass() != o.getClass()) return false;
Card card = (Card) o;
//If the numbers are the same and the designs and colors are the same, it is logically the same
return rank == card.rank && Objects.equals(suit, card.suit);
}
@Override
public int hashCode() {
return Objects.hash(rank, suit);
}
}
public class TestDemo {
public static void main(String[] args) {
Card card1 = new Card(1, "♥");
Card card2 = new Card(1, "♥");
System.out.println(card1.equals(card2));
}3.2 comparison based on Comparble interface classes
In order to have the ability of comparison, the Comparable interface is implemented here to compare the specified parts you need (the default here is the comparison of small heaps)
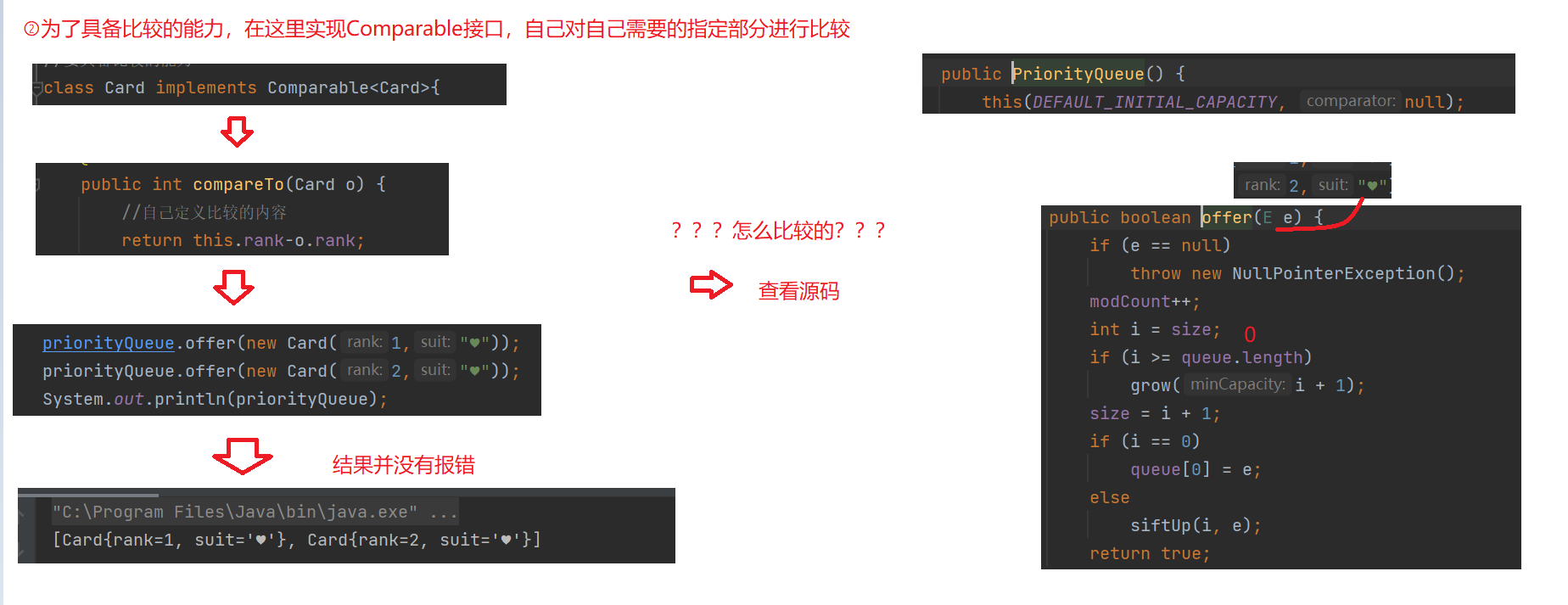
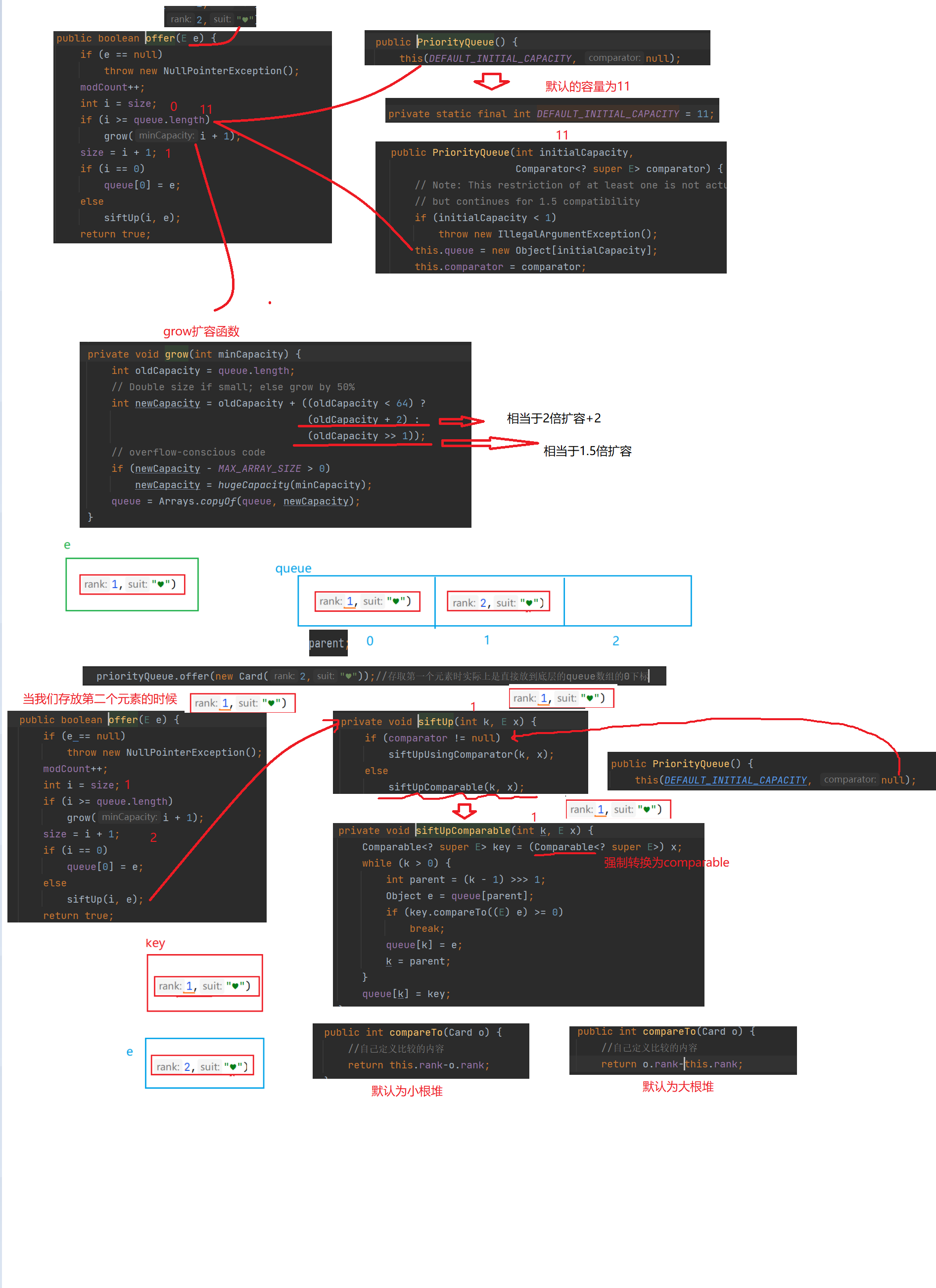
The code is as follows:
import java.util.PriorityQueue;
//Have the ability to compare
class Card implements Comparable<Card>{
public int rank;
public String suit;
public Card(int rank, String suit) {
this.rank = rank;
this.suit = suit;
}
@Override
public String toString() {
return "Card{" +
"rank=" + rank +
", suit='" + suit + '\'' +
'}';
}
@Override
public int compareTo(Card o) {
//Define the content of comparison
return o.rank-this.rank;
}
}
public class TestDemo {
public static void main(String[] args) {
//The default bottom layer is the small root heap, and each element stored will be compared
PriorityQueue<Card>priorityQueue=new PriorityQueue<>();
priorityQueue.offer(new Card(2,"♥"));//When accessing the first element, it is actually put directly into the 0 subscript of the underlying queue array
priorityQueue.offer(new Card(1,"♥"));
System.out.println(priorityQueue);
}3.3 comparator based comparison
The code is as follows:
import java.util.Comparator;
import java.util.PriorityQueue;
//Have the ability to compare
class Card{
public int rank;
public String suit;
public Card(int rank, String suit) {
this.rank = rank;
this.suit = suit;
}
@Override
public String toString() {
return "Card{" +
"rank=" + rank +
", suit='" + suit + '\'' +
'}';
}
}
class RankCompartor implements Comparator<Card>{
@Override
public int compare(Card o1, Card o2) {
return o1.rank-o2.rank;
}
}
public class TestDemo {
public static void main(String[] args) {
//The default bottom layer is the small root heap, and each element stored will be compared
Card card1=new Card(1,"♥");
Card card2=new Card(2,"♥");
RankCompartor rankCompartor=new RankCompartor();
int ret=rankCompartor.compare(card1,card2);
System.out.println(ret);
}The following two methods can also be used:
Method ①: anonymous inner class
PriorityQueue<Card> priorityQueue = new PriorityQueue<>(new Comparator<Card>() {
@Override
public int compare(Card o1, Card o2) {
return o1.rank-o2.rank;
}
});Method ②: lambda expression
PriorityQueue<Card> priorityQueue = new PriorityQueue<>((x,y)->{return y.rank-x.rank;});3.4 comparison of three methods

compareTo has a strong inclination to classes
6. Problems left over from last class
6.1 TOPK issues

Idea ①: sort the whole and output the top 10 largest elements. (conventional thinking)
Train of thought ②: use the heap just learned before
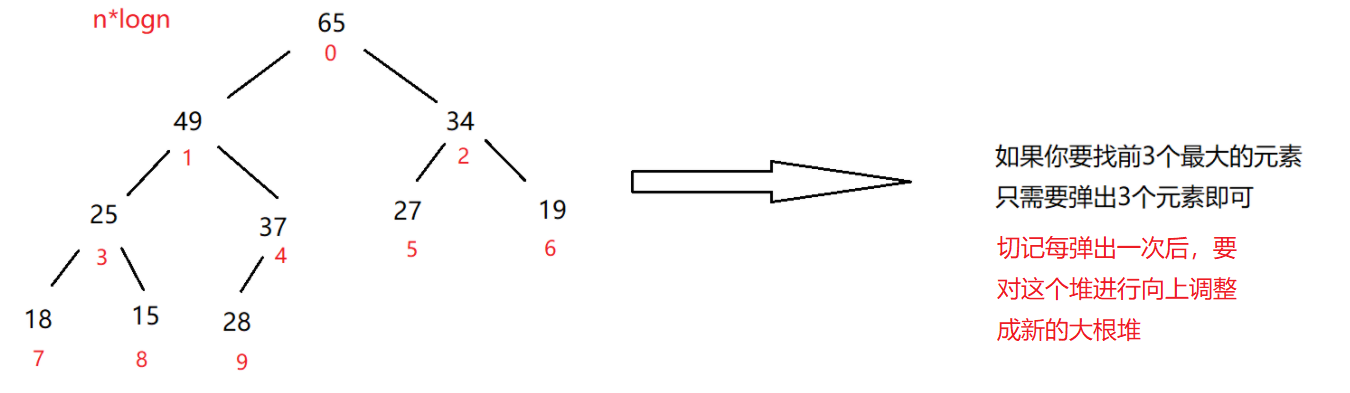
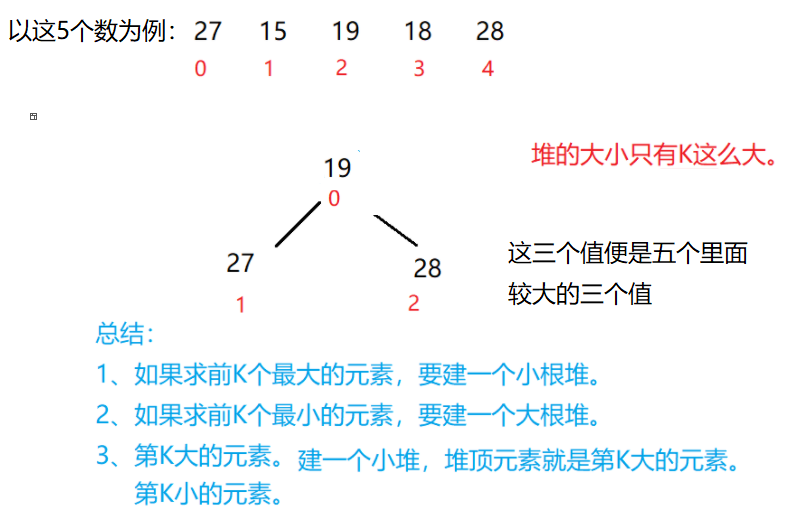
Idea ③: A. first create the first three elements as a small root heap
b. because the current heap is a small root heap, the top element must be the smaller of the first k elements. If the existing element is larger than the top element, it will replace the top element. At the same time, this element may be one of the topk. On the contrary, if it is a large root pile, it is not necessarily
c. after the top element is removed, adjust it to a small root pile again
The code is as follows:
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
//Find the first k smallest elements in the array and build a lot
public class TopK {
public static int[] topK(int []array,int k){
//Create a large root heap of size k
PriorityQueue<Integer> maxHeap=new PriorityQueue<>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
});
//Traverse the elements in the array and put the first k elements into the queue
for (int i = 0; i < array.length ; i++) {
if(maxHeap.size()<k){
maxHeap.offer(array[i]);
}else{
//Starting with k+1 elements, each element is compared with the top element
int top=maxHeap.peek();
if(top>array[i]){
//The big one will now pop up
maxHeap.poll();
//Then deposit the small ones
maxHeap.offer(array[i]);
}
}
}
int[]tmp=new int[k];
for (int i = 0; i <k ; i++) {
tmp[i]=maxHeap.poll();
}
return tmp;
}
public static void main(String[] args) {
int []array={18,21,8,10,34,12};
int []tmp=topK(array,3);
System.out.println(Arrays.toString(tmp));
}
}Heap sort problem:
Solution idea: (end condition is 0)
① Adjust the heap to a large root heap
② 0 subscript can be exchanged with the last unordered element
③end--
④ Adjust the heap down to the big root heap again

The code is as follows:
public void heapSort() {
int end = this.usedSize - 1;
while (end > 0) {
int tmp = elem[0];
elem[0] = elem[end];
elem[end] = tmp;
shiftDown(0, end);
end--;
}
}6.2} face to face questions
Title:
Given two integer arrays nums1 and nums2 arranged in ascending order, and an integer k.
Define a pair of values (u,v), where the first element is from nums1 and the second element is from nums2.
Please find the minimum k# number pairs (u1,v1), (u2,v2) (uk,vk) .
Solution: (in fact, it is also a topK problem. The difference is that it is changed to the smallest sum of the first k)
??? The problem is??? How to put a group of pairs
PriorityQueue<List<Integer>>
The code is as follows:
public static List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
PriorityQueue<List<Integer>> maxHeap = new PriorityQueue<>(k, new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> o1, List<Integer> o2) {
//To get an element in the List, you need to use the get() method
return (o2.get(0)+o2.get(1))-(o1.get(0)+o1.get(1));
}
});
// for (int i = 0; i < Math.min(nums1.length,k); i++) {
// for (int j = 0; j < Math.min(nums2.length,k); j++) {
for (int i = 0; i < nums1.length; i++) {
for (int j = 0; j < nums2.length; j++) {
//Before it's full
if(maxHeap.size() < k) {
List<Integer> tmpList = new ArrayList<>();
tmpList.add(nums1[i]);
tmpList.add(nums2[j]);
maxHeap.offer(tmpList);
}else {
//Gets the value of the top element
int top = maxHeap.peek().get(0) + maxHeap.peek().get(1);
if(top > nums1[i]+nums2[j]) {
//Remember what you want to pop up
maxHeap.poll();
List<Integer> tmpList = new ArrayList<>();
tmpList.add(nums1[i]);
tmpList.add(nums2[j]);
maxHeap.offer(tmpList);
}
}
}
}
List<List<Integer>> ret = new ArrayList<>();
for (int i = 0; i < k && !maxHeap.isEmpty(); i++) {
ret.add(maxHeap.poll());
}
return ret;
}
public static void main(String[] args) {
int[] nums1 = {1,7,11};
int[] nums2 = {2,4,6};
List<List<Integer>> ret = kSmallestPairs(nums1,nums2,3);
System.out.println(ret);
}
Thanks for reading~~~


 https://leetcode-cn.com/problems/find-k-pairs-with-smallest-sums/
https://leetcode-cn.com/problems/find-k-pairs-with-smallest-sums/