| ① Complete collection of classic algorithms in C language (recommended Collection) 👈 |
one 💜 Tower of Hanoi
explain
The towers of Hanoi was brought to France by French M.Claus(Lucas) from Thailand in 1883. Hanoi was the capital of North Vietnam during the Vietnam War, which is now Ho Chi Minh City; In 1883, the French mathematician Edouard Lucas mentioned this story. It is said that Benares had a Baltic tower at the time of Genesis, It is supported by three diamond sticks (Pag). At the beginning, God placed 64 gold plates arranged from top to bottom from small to large on the first stick (Disc) and ordered the monks to move all the gold plates from the first stone rod to the third stone rod, and abide by the principle of large plates under small plates. If only one plate is moved every day, the tower will be damaged when all the plates are moved, that is, when the end of the world comes.
solution
If the column is marked ABC, move it from A to C. when there is only one plate, move it directly to C. when there are two plates, use B as an auxiliary column. If the number of disks exceeds 2, it is very simple to cover the plates below the third. Process two plates at A time, that is, the three steps of A - > b, A - > C and B - > C. The covered part actually enters the recursive processing of the program. In fact, if there are n plates, the number of times required to complete the movement is 2^n - 1, so when the number of plates is 64, the number of times required is:
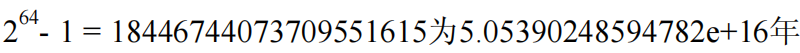
That is, about the 5000 century, if there is no concept of this number, let's assume that one plate is moved every second, which will be about 585 billion years.
#include <stdio.h>
void hanoi(int n, char A, char B, char C) {
if(n == 1) {
printf("Move sheet %d from %c to %c\n", n, A, C);
}
else {
hanoi(n-1,A, C, B);
printf("Move sheet %d from %c to %c\n", n, A, C);
hanoi(n-1, B,A, C);
}
}
int main() {
int n;
printf("Please enter the number of disks:");
scanf("%d", &n);
hanoi(n, 'A', 'B', 'C');
return 0;
}
two 😄 Fibonacci sequence
explain
Fibonacci was a European mathematician in the 1200's, In his work, he once said, "if there is an immune child, one small immune child is born every month, and one month later, the small immune child also begins to give birth. At first, there is only one immune child, one month later, there are two immune children, two months later, there are three immune children, and three months later, there are five immune children (xiaomianzi is put into production).... if you don't quite understand this example, take a picture to know. Note that the newborn xiaomianzi will not be put into production until it grows for one month. A similar principle can also be used for plant growth. This is Fibonacci series, which is commonly called Fisher series, such as the following:
1,1 ,2,3,5,8,13,21,34,55,89...
solution
According to the description, we can define the Fisher sequence as follows:

#include <stdio.h>
#include <stdlib.h>
#define N 20
int main(void) {
int Fib[N] = {0};
int i;
Fib[0] = 0;
Fib[1] = 1;
for(i = 2; i < N; i++)
Fib[i] = Fib[i-1] + Fib[i-2];
for(i = 0; i < N; i++)
printf("%d ", Fib[i]);
printf("\n");
return 0;
}
Operation results

three 👍 Pascal triangle

#include <stdio.h>
#define N 12
long combi(int n, int r){
int i;
long p = 1;
for(i = 1; i <= r; i++)
p = p * (n-i+1) / i;
return p;
}
void main() {
int n, r, t;
for(n = 0; n <= N; n++) {
for(r = 0; r <= n; r++) {
int i;/* Typesetting start */
if(r == 0) {
for(i = 0; i <= (N-n); i++)
printf(" ");
}else {
printf(" ");
} /* End of typesetting */
printf("%3d", combi(n, r));
}
printf("\n");
}
}
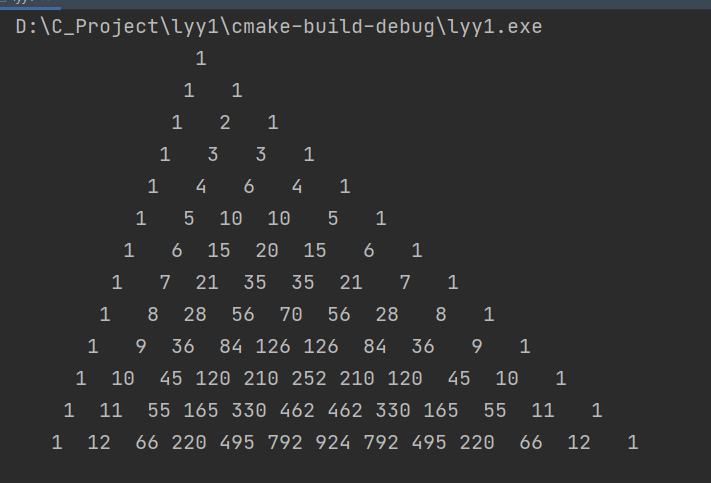
Operation results
four 🌝 Tricolor chess
explain
The problem of the three color flag was first raised by E.W.Dijkstra. His term is Dutch Nation Flag(Dijkstra is Dutch), and most authors use three color flag.
Suppose there is a rope with red, white and blue flags on it. At first, the colors of the flags on the rope are not in order. You want to classify them and arrange them in the order of blue, white and red. How to move the least times? Note that you can only do this action on the rope, and you can only change two flags at a time.
solution
Moving on a rope means that only one array can be used in the program instead of other arrays. The solution to the problem is very simple. You can imagine moving the flag from the beginning of the rope, moving forward when you encounter blue, leaving white in the middle and moving back when you encounter red, as shown below:
Just to minimize the number of moves, you need some skills:
If the position of W in the figure is white, W+1 indicates that the unprocessed part is moved to the white group.
If part W is blue, the elements of B and W are swapped, and B and W must each + 1, indicating that there is one more element in both groups.
If the position of W is red, exchange w with R, but r should be reduced by 1, indicating that the unprocessed part should be reduced by 1.
Note that B, W and R are not the number of tricolor flags, they are just moving indicators; When does the move end? At the beginning, the unprocessed r index will be equal to the total number of flags. When the index number of R is reduced to less than the index number of W, it means that the next flags are red. At this time, the movement can be ended, as shown below:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define BLUE 'b'
#define WHITE 'w'
#define RED 'r'
#define SWAP(x, y) { char temp; \
temp = color[x]; \
color[x] = color[y]; \
color[y] = temp; }
int main() {
char color[] = {'r', 'w', 'b', 'w', 'w',
'b', 'r', 'b', 'w', 'r', '\0'};
int wFlag = 0;
int bFlag = 0;
int rFlag = strlen(color) - 1;
int i;
for(i = 0; i < strlen(color); i++)
printf("%c ", color[i]);
printf("\n");
while(wFlag <= rFlag) {
if(color[wFlag] == WHITE)
wFlag++;
else if(color[wFlag] == BLUE) {
SWAP(bFlag, wFlag);
bFlag++; wFlag++;
}
else {
while(wFlag < rFlag && color[rFlag] == RED)
rFlag--;
SWAP(rFlag, wFlag);
rFlag--;
} }
for(i = 0; i < strlen(color); i++)
printf("%c ", color[i]);
printf("\n");
return 0;
}
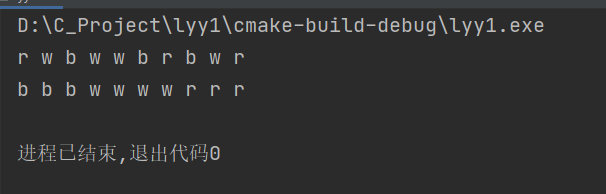
Operation results
five 🌔 Rat wandering Officer (I)
explain
Mouse walking maze is the basic problem type of recursive solution. In the two-dimensional array, we use 2 to represent the maze wall and 1 to represent the walking path of mouse. Try to find the path from entrance to exit by program.
solution
The mouse moves in four directions: up, left, down and right. After each grid, select one direction to move forward. If it cannot move forward, go back and select the next forward direction. In this way, test the four directions in order in the array until it reaches the exit. This is the basic problem of recursion. Please read the program directly.
#include <stdio.h>
#include <stdlib.h>
int visit(int, int);
int maze[7][7] = {{2, 2, 2, 2, 2, 2, 2},
{2, 0, 0, 0, 0, 0, 2},
{2, 0, 2, 0, 2, 0, 2},
{2, 0, 0, 2, 0, 2, 2},
{2, 2, 0, 2, 0, 2, 2},
{2, 0, 0, 0, 0, 0, 2},
{2, 2, 2, 2, 2, 2, 2}};
int startI = 1, startJ = 1; // entrance
int endI = 5, endJ = 5; // Export
int success = 0;
int main(void) {
int i, j;
printf("Show maze:\n");
for(i = 0; i < 7; i++) {
for(j = 0; j < 7; j++)
if(maze[i][j] == 2)
printf("█");
else
printf(" ");
printf("\n");
}
if(visit(startI, startJ) == 0)
printf("\n No exit found!\n");
else {
printf("\n Display path:\n");
for(i = 0; i < 7; i++) {
for(j = 0; j < 7; j++) {
if(maze[i][j] == 2)
printf("█");
else if(maze[i][j] == 1)
printf("◇");
else
printf(" ");
}
printf("\n");
} }
return 0;
}
int visit(int i, int j) {
maze[i][j] = 1;
if(i == endI && j == endJ)
success = 1;
if(success != 1 && maze[i][j+1] == 0) visit(i, j+1);
if(success != 1 && maze[i+1][j] == 0) visit(i+1, j);
if(success != 1 && maze[i][j-1] == 0) visit(i, j-1);
if(success != 1 && maze[i-1][j] == 0) visit(i-1, j);
if(success != 1)
maze[i][j] = 0;
return success;
}
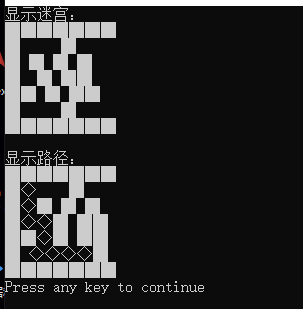
Operation results
six 🏀 Rat wandering Officer (2)
explain
Due to the design of the maze, there may be more than one path from the entrance to the exit of the maze. How to find all the paths?
solution
Finding all paths seems complicated, but it's actually simpler. Just show the path when the mouse goes to the exit, then return to the previous grid and reselect the next location to continue recursion. It's simpler than finding a single path. Our program just needs to make a little modification.
#include <stdio.h>
#include <stdlib.h>
void visit(int, int);
int maze[9][9] = {{2, 2, 2, 2, 2, 2, 2, 2, 2},
{2, 0, 0, 0, 0, 0, 0, 0, 2},
{2, 0, 2, 2, 0, 2, 2, 0, 2},
{2, 0, 2, 0, 0, 2, 0, 0, 2},
{2, 0, 2, 0, 2, 0, 2, 0, 2},
{2, 0, 0, 0, 0, 0, 2, 0, 2},
{2, 2, 0, 2, 2, 0, 2, 2, 2},
{2, 0, 0, 0, 0, 0, 0, 0, 2},
{2, 2, 2, 2, 2, 2, 2, 2, 2}};
int startI = 1, startJ = 1; // entrance
int endI = 7, endJ = 7; // Export
int main(void) {
int i, j;
printf("Show maze:\n");
for(i = 0; i < 7; i++) {
for(j = 0; j < 7; j++)
if(maze[i][j] == 2)
printf("█");
else
printf(" ");
printf("\n");
}
visit(startI, startJ);
return 0;
}
void visit(int i, int j) {
int m, n;
maze[i][j] = 1;
if(i == endI && j == endJ) {
printf("\n Display path:\n");
for(m = 0; m < 9; m++) {
for(n = 0; n < 9; n++)
if(maze[m][n] == 2)
printf("█");
else if(maze[m][n] == 1)
printf("◇");
else
printf(" ");
printf("\n");
} }
if(maze[i][j+1] == 0) visit(i, j+1);
if(maze[i+1][j] == 0) visit(i+1, j);
if(maze[i][j-1] == 0) visit(i, j-1);
if(maze[i-1][j] == 0) visit(i-1, j);
maze[i][j] = 0;
}
Operation results

seven 🍪 knight tour
explain
Knight tour attracted the attention of mathematicians and puzzle fans at the beginning of the 18th century. When it was put forward can not be tested. The knight's walking method is the walking method of chess. The knight can start from any position. How can it finish [all positions?
solution
Basically, the knight's walking method can be solved by recursion, but pure recursion is quite inefficient when the dimension is large. A smart solution was put forward by J.C. Warnsdorff in 1823. In short, after completing the most difficult position first, the next road will be broad. The next step to be taken by the knight is "the step with the least number of steps to take when choosing for the next step", Using this method, you can have a high probability of finding the walking method without recursion (there are also chances of not finding the walking method).
#include <stdio.h>
int board[8][8] = {0};
int main(void) {
int startx, starty;
int i, j;
printf("Enter starting point:");
scanf("%d %d", &startx, &starty);
if(travel(startx, starty)) {
printf("Tour completed!\n");
}
else {
printf("Travel failed!\n");
}
for(i = 0; i < 8; i++) {
for(j = 0; j < 8; j++) {
printf("%2d ", board[i][j]);
}
putchar('\n');
}
return 0;
}
int travel(int x, int y) {
// Corresponding to the eight directions that the knight can go
int ktmove1[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int ktmove2[8] = {1, 2, 2, 1, -1, -2, -2, -1};
// Test the way out for the next step
int nexti[8] = {0};
int nextj[8] = {0};
// Record the number of outlets
int exists[8] = {0};
int i, j, k, m, l;
int tmpi, tmpj;
int count, min, tmp;
i = x;
j = y;
board[i][j] = 1;
for(m = 2; m <= 64; m++) {
for(l = 0; l < 8; l++)
exists[l] = 0;
l = 0;
// Explore eight directions
for(k = 0; k < 8; k++) {
tmpi = i + ktmove1[k];
tmpj = j + ktmove2[k];
// If it's the border, you can't go
if(tmpi < 0 || tmpj < 0 || tmpi > 7 || tmpj > 7)
continue;
// If you can go in this direction, record it
if(board[tmpi][tmpj] == 0) {
nexti[l] = tmpi;
nextj[l] = tmpj;
// Add one in the direction you can go
l++;
} }
count = l;
// If there are 0 walking directions, return
if(count == 0) {
return 0;
}
else if(count == 1) {
// There is only one direction to go
// So direct is the least way out
min = 0;
}
else {
// Find the number of outlets for the next location
for(l = 0; l < count; l++) {
for(k = 0; k < 8; k++) {
tmpi = nexti[l] + ktmove1[k];
tmpj = nextj[l] + ktmove2[k];
if(tmpi < 0 || tmpj < 0 ||
tmpi > 7 || tmpj > 7) {
continue;
}
if(board[tmpi][tmpj] == 0)
exists[l]++;
} }
tmp = exists[0];
min = 0;
// Look for the direction with the least way out from the directions that can be taken
for(l = 1; l < count; l++) {
if(exists[l] < tmp) {
tmp = exists[l];
min = l;
} }
}
// Take the direction of the least way out
i = nexti[min];
j = nextj[min];
board[i][j] = m;
}
return 1;
}
eight 🍏 Eight queens
explain
Queens in chess can move forward in a straight line and eat all the pieces they encounter. If there are eight queens on the chessboard, how can these eight queens be placed on the chessboard safely? In 1970 and 1971, E.W.Dijkstra and N.Wirth used this problem to explain the skills of programming.
solution
The problem of chessboard can be solved by recursion, but how to reduce the number of recursion? In the eight queens problem, it is not necessary to check all the grids. For example, if a column is checked, the other grids of the column do not need to be checked. This method is called branch pruning.
#include <stdio.h>
#include <stdlib.h>
#define N 8
int column[N+1]; // Whether there is a queen in the same column, 1 means yes
int rup[2*N+1]; // Is there a queen from top right to bottom left
int lup[2*N+1]; // Is there a queen from top left to bottom right
int queen[N+1] = {0};
int num; // Answer number
void backtrack(int); // Recursive solution
int main(void) {
int i;
num = 0;
for(i = 1; i <= N; i++)
column[i] = 1;
for(i = 1; i <= 2*N; i++)
rup[i] = lup[i] = 1;
backtrack(1);
return 0;
}
void showAnswer() {
int x, y;
printf("\n answer %d\n", ++num);
for(y = 1; y <= N; y++) {
for(x = 1; x <= N; x++) {
if(queen[y] == x) {
printf(" Q");
}
else {
printf(" .");
} }
printf("\n");
}
}
void backtrack(int i) {
int j;
if(i > N) {
showAnswer();
}
else {
for(j = 1; j <= N; j++) {
if(column[j] == 1 &&
rup[i+j] == 1 && lup[i-j+N] == 1) {
queen[i] = j;
// Set to occupied
column[j] = rup[i+j] = lup[i-j+N] = 0;
backtrack(i+1);
column[j] = rup[i+j] = lup[i-j+N] = 1;
}
}
}
}
Operation results
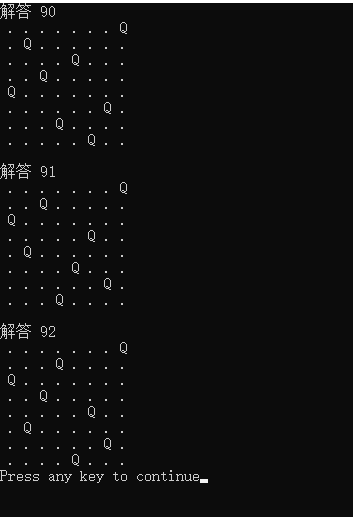
nine 🍒 Eight silver coins
explain
There are eight silver coins a b c d e f g h. It is known that one of them is a counterfeit coin, and its weight is different from the real coin, but it is unknown whether it is lighter or heavier. How to use the balance to determine which is a counterfeit coin with the least number of comparisons, and know that the counterfeit coin is lighter or heavier than the real coin.
solution
It is not difficult to find counterfeit money alone, but the problem is limited to the minimum number of comparisons, so we can't solve it by simple loop comparison, We can use the decision tree and use analysis and tree view to help solve the problem. A simple situation is that we compare a+b+c with d+e+f. if it is equal, the counterfeit currency must be g or h. We first compare g or h which is heavier. If G is heavier, we compare it with a (a is real money). If G is equal to a, then G is real money and H is counterfeit money. Since h is lighter than g and G is real money, the weight of H counterfeit money is lighter than real money.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
void compare(int[], int, int, int);
void eightcoins(int[]);
int main(void) {
int coins[8] = {0};
int i;
srand(time(NULL));
for(i = 0; i < 8; i++)
coins[i] = 10;
printf("\n Enter counterfeit weight(Larger or smaller than 10): ");
scanf("%d", &i);
coins[rand() % 8] = i;
eightcoins(coins);
printf("\n\n List all coin weights:");
for(i = 0; i < 8; i++)
printf("%d ", coins[i]);
printf("\n");
return 0;
}
void compare(int coins[], int i, int j, int k) {
if(coins[i] > coins[k])
printf("\n Counterfeit money %d Heavier", i+1);
else
printf("\n Counterfeit money %d Lighter", j+1);
}
void eightcoins(int coins[]) {
if(coins[0]+coins[1]+coins[2] ==
coins[3]+coins[4]+coins[5]) {
if(coins[6] > coins[7])
compare(coins, 6, 7, 0);
else
compare(coins, 7, 6, 0);
}
else if(coins[0]+coins[1]+coins[2] >
coins[3]+coins[4]+coins[5]) {
if(coins[0]+coins[3] == coins[1]+coins[4])
compare(coins, 2, 5, 0);
else if(coins[0]+coins[3] > coins[1]+coins[4])
compare(coins, 0, 4, 1);
if(coins[0]+coins[3] < coins[1]+coins[4])
compare(coins, 1, 3, 0);
}
else if(coins[0]+coins[1]+coins[2] <
coins[3]+coins[4]+coins[5]) {
if(coins[0]+coins[3] == coins[1]+coins[4])
compare(coins, 5, 2, 0);
else if(coins[0]+coins[3] > coins[1]+coins[4])
compare(coins, 3, 1, 0);
if(coins[0]+coins[3] < coins[1]+coins[4])
compare(coins, 4, 0, 1);
}
}
Operation results
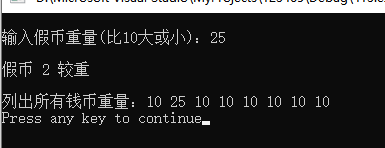
ten 💣 Life game
explain
The game of life was proposed by the British mathematician J. H. Conway in 1970. The neighbors of a cell include upper, lower, left, right, upper left, lower left, upper right and lower right adjacent cells. The rules of the game are as follows:
Lonely death: if a cell has less than one neighbor, the cell will die in the next state.
Crowded death: if the cell has more than four neighbors, the cell will die in the next state.
Stable: if the cell has two or three neighbors, the next state is stable survival.
Resurrection: if there are no cells in a location and there are three neighbors in the location, a cell will be resurrected in the location.
solution
The rules of the life game can be simplified as follows, and can be implemented using the program by using CASE comparison:
When the number of neighbors is 0, 1, 4, 5, 6, 7 and 8, the next state of the cell is death.
When the number of neighbors is 2, the next state of the cell is resurrection.
When the number of neighbors is 3, the next state of the cell is stable.
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#define MAXROW 10
#define MAXCOL 25
#define DEAD 0
#define ALIVE 1
int map[MAXROW][MAXCOL], newmap[MAXROW][MAXCOL];
void init();
int neighbors(int, int);
void outputMap();
void copyMap();
int main() {
int row, col;
char ans;
init();
while(1) {
outputMap();
for(row = 0; row < MAXROW; row++) {
for(col = 0; col < MAXCOL; col++) {
switch (neighbors(row, col)) {
case 0:
case 1:
case 4:
case 5:
case 6:
case 7:
case 8:
newmap[row][col] = DEAD;
break;
case 2:
newmap[row][col] = map[row][col];
break;
case 3:
newmap[row][col] = ALIVE;
break;
} } }
copyMap();
printf("\nContinue next Generation ? ");
getchar();
ans = toupper(getchar());
if(ans != 'Y') break;
}
return 0;
}
void init() {
int row, col;
for(row = 0; row < MAXROW; row++)
for(col = 0; col < MAXCOL; col++)
map[row][col] = DEAD;
puts("Game of life Program");
puts("Enter x, y where x, y is living cell");
printf("0 <= x <= %d, 0 <= y <= %d\n",
MAXROW-1, MAXCOL-1);
puts("Terminate with x, y = -1, -1");
while(1) {
scanf("%d %d", &row, &col);
if(0 <= row && row < MAXROW &&
0 <= col && col < MAXCOL)
map[row][col] = ALIVE;
else if(row == -1 || col == -1)
break;
else
printf("(x, y) exceeds map ranage!");
}
}
int neighbors(int row, int col) {
int count = 0, c, r;
for(r = row-1; r <= row+1; r++)
for(c = col-1; c <= col+1; c++) {
if(r < 0 || r >= MAXROW || c < 0 || c >= MAXCOL)
continue;
if(map[r][c] == ALIVE)
count++;
}
if(map[row][col] == ALIVE)
count--;
return count;
}
void outputMap() {
int row, col;
printf("\n\n%20cGame of life cell status\n");
for(row = 0; row < MAXROW; row++) {
printf("\n%20c", ' ');
for(col = 0; col < MAXCOL; col++)
if(map[row][col] == ALIVE) putchar('#');
else putchar('-');
}
}
void copyMap() {
int row, col;
for(row = 0; row < MAXROW; row++)
for(col = 0; col < MAXCOL; col++)
map[row][col] = newmap[row][col];
}
Operation results

eleven 🔔 String check
explain
Today, some high-level programming languages have more and more powerful support for string processing (such as Java, Perl, etc.), but string search itself is still a topic worthy of discussion. Here, Boyer Moore method is used to illustrate how to carry out string description. This method is fast and its principle is simple and easy to understand.
solution
String search itself is not difficult, and it can also be solved by using the violence method, but how to quickly search a string is not simple. The traditional string search starts from the comparison between the keyword and the beginning of the string, such as Knuth Morris Pratt algorithm string search. This method is also good, but it takes time to calculate the formula; Boyer Moore string check starts from the back of the keyword, and makes a forward table. If the comparison is inconsistent, advance to the next check according to the value in the forward table, assuming that P is good, and then compare whether the value of p-n+1 to P in the string is the same as the keyword.
If there are repeated characters in the keyword, the forward value will have more than two values. At this time, the value with smaller forward value will be taken, so possible positions will not be skipped. For example, for the keyword texture, the forward value of t should take the following 3 instead of the previous 7.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void table(char*); // Create forward table
int search(int, char*, char*); // Search keywords
void substring(char*, char*, int, int); // Fetch substring
int skip[256];
int main(void) {
char str_input[80];
char str_key[80];
char tmp[80] = {'\0'};
int m, n, p;
printf("Please enter a string:");
gets(str_input);
printf("Please enter search keywords:");
gets(str_key);
m = strlen(str_input); // Calculate string length
n = strlen(str_key);
table(str_key);
p = search(n-1,str_input,str_key);
while(p != -1) {
substring(str_input, tmp, p, m);
printf("%s\n", tmp);
p = search(p+n+1,str_input,str_key);
}
printf("\n");
return 0;
}
void table(char *key) {
int k, n;
n = strlen(key);
for(k = 0; k <= 255; k++)
skip[k] = n;
for(k = 0; k < n - 1; k++)
skip[key[k]] = n - k - 1;
}
int search(int p, char* input, char* key) {
int i, m, n;
char tmp[80] = {'\0'};
m = strlen(input);
n = strlen(key);
while(p < m) {
substring(input, tmp, p-n+1, p);
if(!strcmp(tmp, key)) // Compare whether the two strings are the same
return p-n+1;
p += skip[input[p]];
}
return -1;
}
void substring(char *text, char* tmp, int s, int e) {
int i, j;
for(i = s, j = 0; i <= e; i++, j++)
tmp[j] = text[i];
tmp[j] = '\0';
}
Operation results
twelve 💝 Two color and three color Hanoi Tower
explain
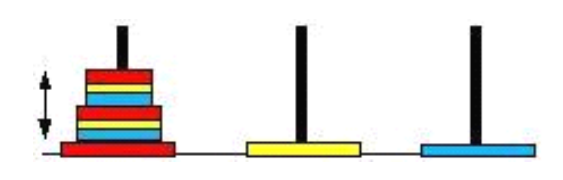
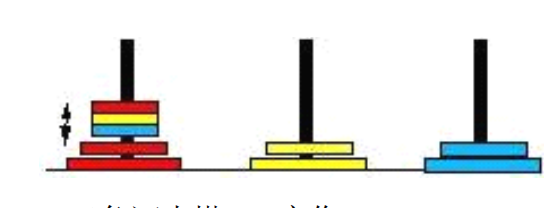
The two-color Hanoi Tower and the three-color Hanoi tower are derived from the Hanoi Tower rules introduced earlier. The purpose of the two-color Hanoi tower is to move the ring position at the top left of the figure below to the ring position at the bottom right:
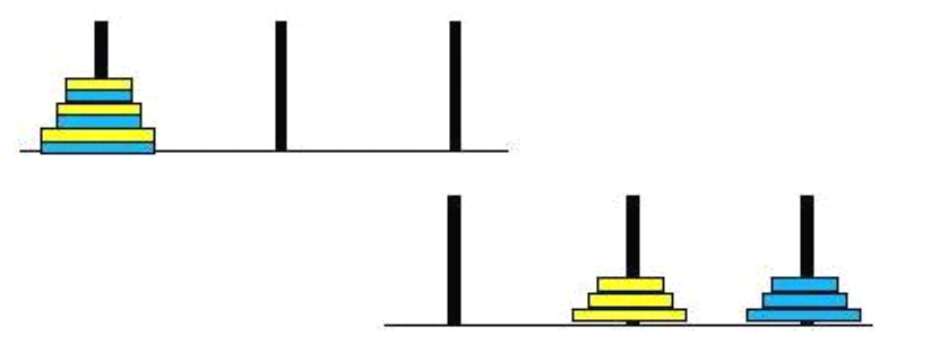
The three color Hanoi Tower moves the ring at the top left of the figure below to the ring at the top right:
solution
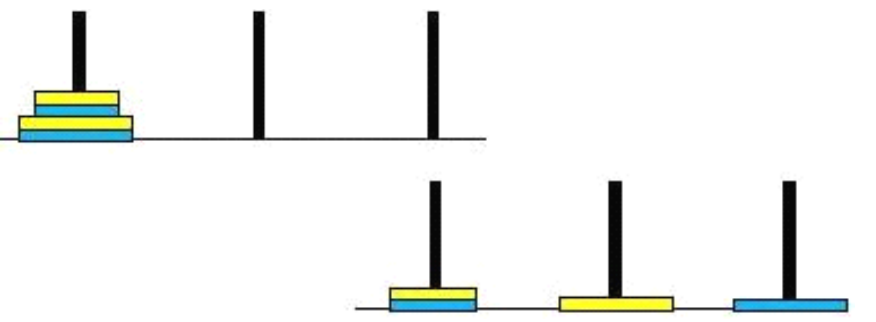
Whether it is the two-color Hanoi tower or the three-color Hanoi Tower, the solution concept is similar to that of the Hanoi Tower introduced before, and the recursive solution is also used. However, the purpose of this recursive solution is different. Let's first look at the case where there are only two plates, which is very simple. Just move the yellow of the first column to the second column, and then the blue of the first column to the third column. In the case of four disks, you must first complete the movement from top left to bottom right in the figure below by recursion:
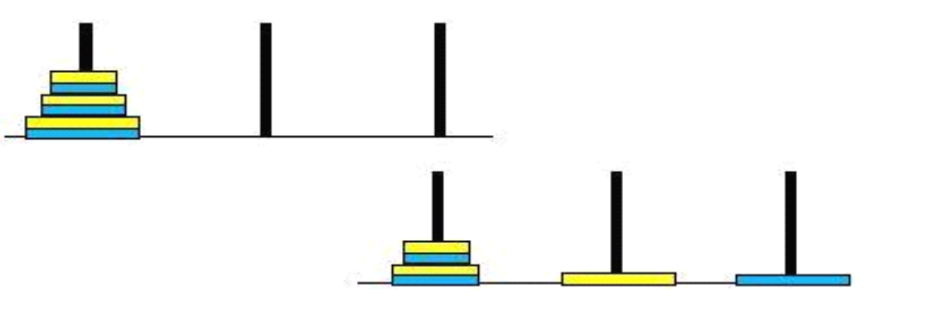
Next, don't worry about them at the bottom, because they are already positioned. Just deal with the upper two plates of the first column. What about the six disks? Same! First, you must complete the movement from top left to bottom right in the figure below with recursion:
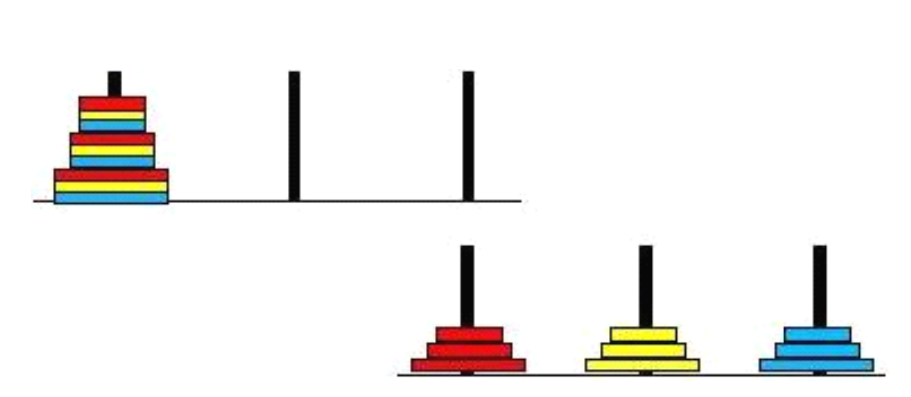
Next, don't worry about them at the bottom, because they are already positioned. Just deal with the four plates on the first column, which is the same as the previous situation of only four plates. Next, you will know how to solve the problem. Whether it is eight plates or more than ten plates, you use this concept to solve the problem. What about the three color Hanoi Tower? Similarly, to directly look at the nine disks, you must first complete the moving results in the figure below:
Next, the bottom two layers don't care about them, because they are already positioned, just deal with the three plates above the first column
That's it.
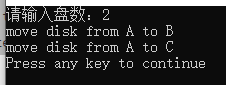
Implementation of bicolor Hanoi Tower C
#include <stdio.h>
void hanoi(int disks, char source, char temp, char target) {
if (disks == 1) {
printf("move disk from %c to %c\n",source, target);
printf("move disk from %c to %c\n",source, target);
} else {
hanoi(disks-1,source, target, temp);
hanoi(1,source, temp, target);
hanoi(disks-1, temp, source, target);
}
}
void hanoi2colors(int disks) {
char source = 'A';
char temp = 'B';
char target = 'C';
int i;
for(i = disks / 2; i > 1; i--) {
hanoi(i-1, source, temp, target);
printf("move disk from %c to %c\n",source, temp);
printf("move disk from %c to %c\n",source, temp);
hanoi(i-1, target, temp, source);
printf("move disk from %c to %c\n", temp, target);
}
printf("move disk from %c to %c\n",source, temp);
printf("move disk from %c to %c\n",source, target);
}
int main() {
int n;
printf("Please enter the number of disks:");
scanf("%d", &n);
hanoi2colors(n);
return 0;
}
Operation results
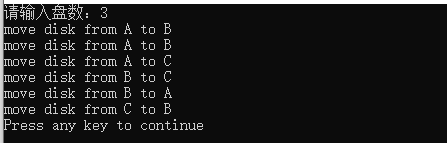
Implementation of Sanse Hanoi Tower C
#include <stdio.h>
void hanoi(int disks, char source, char temp, char target) {
if (disks == 1) {
printf("move disk from %c to %c\n",source, target);
printf("move disk from %c to %c\n",source, target);
printf("move disk from %c to %c\n",source, target);
} else {
hanoi(disks-1,source, target, temp);
hanoi(1,source, temp, target);
hanoi(disks-1, temp, source, target);
}
}
void hanoi3colors(int disks) {
char source = 'A';
char temp = 'B';
char target = 'C';
int i;
if(disks == 3) {
printf("move disk from %c to %c\n",source, temp);
printf("move disk from %c to %c\n",source, temp);
printf("move disk from %c to %c\n",source, target);
printf("move disk from %c to %c\n", temp, target);
printf("move disk from %c to %c\n", temp, source);
printf("move disk from %c to %c\n", target, temp);;
}
else {
hanoi(disks/3-1,source, temp, target);
printf("move disk from %c to %c\n",source, temp);
printf("move disk from %c to %c\n",source, temp);
printf("move disk from %c to %c\n",source, temp);
hanoi(disks/3-1, target, temp, source);
printf("move disk from %c to %c\n", temp, target);
printf("move disk from %c to %c\n", temp, target);
printf("move disk from %c to %c\n", temp, target);
hanoi(disks/3-1,source, target, temp);
printf("move disk from %c to %c\n", target,source);
printf("move disk from %c to %c\n", target,source);
hanoi(disks/3-1, temp, source, target);
printf("move disk from %c to %c\n",source, temp);
for (i = disks / 3 - 1; i > 0; i--) {
if (i>1) {
hanoi(i-1, target,source, temp);
}
printf("move disk from %c to %c\n",target,source);
printf("move disk from %c to %c\n",target,source);
if (i>1) {
hanoi(i-1, temp, source, target);
}
printf("move disk from %c to %c\n",source, temp);
}
}
}
int main() {
int n;
printf("Please enter the number of disks:");
scanf("%d", &n);
hanoi3colors(n);
return 0;
}
Operation results
thirteen 🐑 Knapsack Problem
explain
Suppose there is a backpack with a maximum load of 8kg, and you want to load the total price items available within the load range in the backpack. Suppose the fruit is good, and the number, unit price and weight of the fruit are as follows:
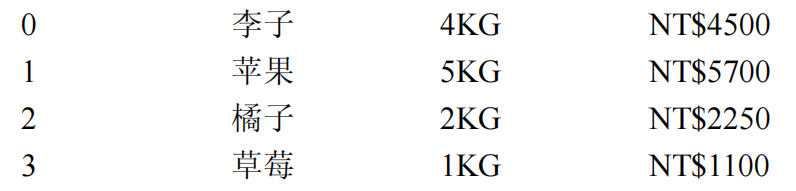

solution
Knapsack problem is a problem about optimization. To solve the optimization problem, you can use "dynamic programming". Starting from the empty set, the best solution of this stage is obtained for each additional element until all the elements are added to the set, and finally the best solution is obtained.
Taking the knapsack problem as an example, we use two arrays, value and item. Value represents the total price of the current optimal solution, item table
Show the last fruit put into the backpack. Suppose there are 8 backpacks with a negative weight of 1 ~ 8, and find the best solution for each backpack.
Gradually put the fruit into the backpack and find the best solution at this stage:
Put in plums

Put in the apple
 Put in oranges
Put in oranges

Add strawberries

Add melon

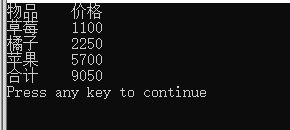
From the last table, we can know that when the backpack weighs 8kg, you can load up to 9050 yuan of fruit, and the last loaded fruit is No. 3, that is, strawberries. Strawberries are loaded, Only 7 kg (8-1) of fruit can be put into the backpack, so we must look at the best solution when the backpack weighs 7 kg. The last one is No. 2, that is, oranges. Now the backpack has a negative weight of 5 kg (7-2), so look at the best solution when the backpack weighs 5 kg. The last one is No. 1, that is, apples. At this time, the backpack has a negative weight of 0 kg (5-5), no more fruit can be added, so the best solution is to add strawberries, oranges and apples, and the total price is 9050 yuan.
#include <stdio.h>
#include <stdlib.h>
#define LIMIT 8 / / weight limit
#define N 5 / / item type
#define MIN 1 / / minimum weight
struct body {
char name[20];
int size;
int price;
};
typedef struct body object;
int main(void) {
int item[LIMIT+1] = {0};
int value[LIMIT+1] = {0};
int newvalue, i, s, p;
object a[] = {{"plum", 4, 4500},
{"Apple", 5, 5700},
{"a mandarin orange", 2, 2250},
{"strawberry", 1, 1100},
{"muskmelon", 6, 6700}};
for(i = 0; i < N; i++) {
for(s = a[i].size; s <= LIMIT;s++) { p = s - a[i].size;
newvalue = value[p] + a[i].price;
if(newvalue > value[s]) {// Find the best solution of stage
value[s] = newvalue;
item[s] = i;
} } }
printf("goods\t Price\n");
for(i = LIMIT; i >= MIN; i = i - a[item[i]].size) {
printf("%s\t%d\n",
a[item[i]].name, a[item[i]].price);
}
printf("total\t%d\n", value[LIMIT]);
return 0;
}
Operation results
fourteen 🐮 Finding PI by Monte Carlo method
explain
Monte Carlo is the capital of the kingdom of Morocco, which is located on the border of France and Italy and is famous for gambling. Monte Carlo's basic principle is to solve problems with random numbers and area formula. This way of solving problems with probability means gambling. Although there are doubts about accuracy, its thinking direction of problem solving is a way worth learning.
solution
Monte Carlo's solution is applicable to problems related to area, such as finding PI value or elliptical area. Here is how to find PI value; Suppose a circle has a radius of 1, so the quarter circle area is PI, and the square area including this quarter circle is 1, as shown in the figure below:
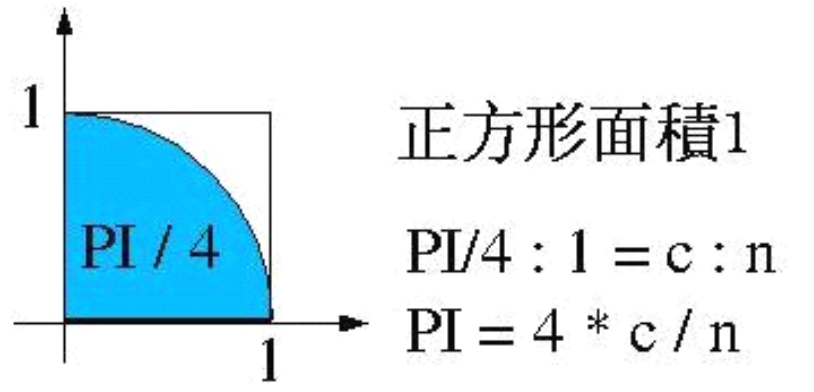
If the flying buoy (point) is projected randomly in the square, some of these flying buoys (points) will fall in the quarter circle. Assuming that the projected flying buoy (point) has n points and the flying buoy (point) in the circle has c points, the final common formula in the figure above will be obtained according to the proportion.
As for how to judge whether the generated point falls in the circle, it is very simple to make the random number generate two values of X and Y. if X2+Y2 is equal to 1, it falls in the circle.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define N 50000
int main(void) {
int i, sum = 0;
double x, y;
srand(time(NULL));
for(i = 1; i < N; i++) { x = (double) rand() / RAND_MAX;
y = (double) rand() / RAND_MAX;
if((x * x + y * y) < 1)
sum++;
}
printf("PI = %f\n", (double) 4 * sum / N);
return 0;
}
Operation results
fifteen 🐱 Filter prime
explain
In addition to itself, numbers that cannot be divided by other integers are called prime numbers. The requirement for prime numbers is very simple, but how to quickly find prime numbers has always been the subject of the efforts of programmers and mathematicians. Here we introduce a famous Eratosthenes method for finding prime numbers.
solution
First of all, we know that this problem can be solved by loop. Divide a specified number by all numbers less than it. If it can be divided, it is not a prime number. However, how to reduce the number of loop checks? How to find all prime numbers less than N?
First, if the number to be checked is n, in fact, it is OK to check to the open root of N. The reason is very simple. Suppose AB = N. if a is greater than the open root of N, in fact, B can be checked before it is less than A. this number can be divided by n. However, using the root opening sign in the program will affect the accuracy, so you can use II < = n to check, and the execution is faster.
Let's assume that there is a sieve storing 1 ~ N, for example:
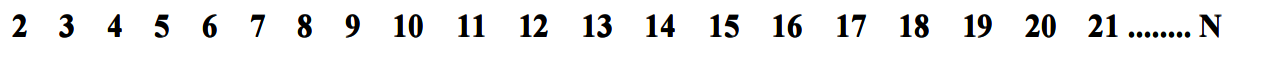
Sift out the multiple of 2 First:
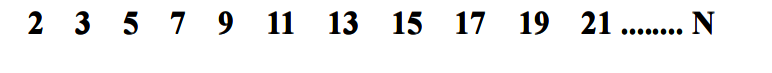
Sieve out the multiples of 3:

Sift the multiple of 5, the prime of 7, and the multiple of 11... In this way, all the numbers left are prime numbers. This is the Eratosthenes Sieve Method.
The number of checks can be further reduced. In fact, just check 6n+1 and 6n+5, that is, directly skip the multiples of 2 and 3, so that the check action of if in the program can be reduced.
#include <stdio.h>
#include <stdlib.h>
#define N 1000
int main(void) {
int i, j;
int prime[N+1];
for(i = 2; i <= N; i++)
prime[i] = 1;
for(i = 2; i*i <= N; i++) { // This can be improved
if(prime[i] == 1) {
for(j = 2*i; j <= N; j++) {
if(j % i == 0)
prime[j] = 0;
} } }
for(i = 2; i < N; i++) {
if(prime[i] == 1) {
printf("%4d ", i);
if(i % 16 == 0)
printf("\n");
} }
printf("\n");
return 0;
}
Operation results