What is a data structure
Data structure is the way that computers store and organize data, and there are one or more specific relationships between them
What is an algorithm
Algorithm: a well-defined calculation process that takes an input and produces an output
The algorithm is a series of calculation steps to convert the input data into the output results
Sorting is a common algorithm
Such as binary search
importance
OJ form of written examination for school recruitment
20-30 multiple-choice questions, 3-4 programming questions
In the school recruitment interview, the weight of data structure and algorithm is very high
Complexity
Algorithm efficiency
Time efficiency
Time complexity
concept
The execution times of basic operations in the algorithm is the time of the algorithm according to the complexity
The time complexity of the algorithm is a function
In practice, time cannot be really calculated (different machines / environments)
Eight cores, that is, eight CPUs and 64g memory
Dual core 4G
Asymptotic representation of large O
Time complexity calculation,large O Progressive representation of---estimate
2n^2+2n+10--->O(n^2)
n->∞Time,f(n)->n^2
The time complexity of the algorithm is a function,In the function expression,The most influential item
Big O notation large O Symbol
Take the highest order,And remove the coefficient
If it's a constant,then is O(1)
Fun(100) You can't think of it as O(1)
Look at the algorithm,Not a specific call
The value passed in by the function can be arbitrary
such as:
strchar("abcdef",'x');//In this call, the string length is 6. Is the complexity O(1)
O(M+N) M,N is a constant
Instead of O(1)
M N doesn't know who is big and who is small

O(1) indicates that it is constant times, and 10W and 100W are also O(1)
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<time.h>
int main()
{
int n = 100000000;
int begin = clock();
for (int i = 0; i < n; ++i)
{
}
int end = clock();
printf("%d\n", end - begin);
//clock displays the timestamp of the beginning of program execution, in milliseconds
//100 million times, only 39 Ms
return 0;
}
Ten thousand times or 100 million times are in the tens of milliseconds level
With the rapid development of hardware, CPU runs too fast
In time complexity calculation, it is usually assumed that the length of array / string is N
Find a data in an array with a length of N, the best time to find it, and the worst n times
Average N/2, but in this case, the default time complexity is the worst
O(N)
Bubble sort:
N-1+...+1=N(N-1)/2—>O(N^2)
void bubble_sort(int arr[], int sz)
{
int i = 0;
int j = 0;
//Number of trips
for ( i = 0; i < sz-1; i++)
{
//Each bubble sorting process
//10 elements 9 Comparison 8 pairs
//Logarithm to be compared - 1 per trip
for (j = 0; j < sz-1-i; j++)
{
if (arr[j+1] < arr[j])//Ascending order
//If it is a string sort, you cannot use the > < sign
{
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
}
practice
Interview question 17.04 Disappearing numbers
The array nums contains all integers from 0 to N, but one of them is missing. Please write code to find the missing integer. Do you have a way to finish it in O(n) time?
If the order of the first row is equal to the order of the second row, the order of the first row is equal to the order of the second row
Or qsort (quick sort) the bottom layer is O(N* logN), which does not meet O(N)
Train of thought 2:0~n calculate the sum of the arithmetic sequence - the addition of the values in the array
O(1) O(N)
Train of thought 2
int missingNumber(int* nums, int numsSize)
{
int n = numsSize+1;
int ret1 =0;
// All values between 0-n accumulate O(1)
for(int i = 0; i < n; i++)
{
ret1 += i;
}
int ret2 = 0;
// All values in the array are accumulated
for(int j = 0; j < numsSize ; j++)
{
ret2 += nums[j];
}
return ret1 - ret2;
}
//Time complexity O(N)
Train of thought 3
Train of thought 3: XOR
0~n Numbers and values in the array are XOR in turn,The result is the missing number
Two identical numbers XOR==0
9 6 4 2 3 5 7 0 1
0 1 2 3 4 5 6 7 8 9
There are only 8 left in XOR
No sorting is required
[3 0 1]
0 1 2 3
3---0011
0---0000
3^0->0011 3
3^0^1-->0011^0001-->0010-->2
0010^0000-->0010
0010^0001-->0011
0011^0010-->0001
0001^0011-->0010--->2
3^0^1^0^1^2^3--->2
1^3^1--->3
There is no need to consider the order of XOR. As long as the final two XORs of the same number are eliminated
int missingNumber(int* nums, int numsSize)
{
int x = 0;
for(int i = 0; i < numsSize + 1; ++i)
{
x ^= i;
}
for(int j = 0; j < numsSize; ++j)
{
x ^= nums[j];
}
return x;
}
//This makes it clearer
int missingNumber(int* nums, int numsSize)
{
int x = 0;
for(int i = 0; i < numsSize + 1; ++i)
{
x ^= i;
if(i < numsSize)
{
x ^= nums[i];
}
}
return x;
}
//Form of a cycle
136. Figures that appear only once
Instead of using extra space, it represents a constant space
Linear time complexity, i.e. O(N)
int singleNumber(int* nums, int numsSize)
{
int x = 0;
for(int i = 0; i<numsSize; i++)
{
x ^= nums[i];
}
return x;
}
Sword finger Offer 56 - I. the number of occurrences of numbers in the array
In an integer array nums, except for two numbers, other numbers appear twice. Please write a program to find these two numbers that only appear once. The time complexity is O(n) and the space complexity is O(1).
ret = 0, XOR all numbers in the array with ret
This eliminates the number of occurrences twice
ret=x^y
2.
ret must not be 0. Find any bit in ret that is 1, indicating that one of the corresponding bits of X and Y is 1 and one is 0
Divide the number in the original array into 1 group if the nth bit is 1 and 0 group if the nth bit is 0
1 3 1 2 5 2
For example, the first digit is 1 and divided into a group, and the first digit is 0 and divided into a group
3 2 2 1 1 5
And then separate them from XOR
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
//returnSize means that the two numbers found are returned in the form of an array
int* singleNumbers(int* nums, int numsSize, int* returnSize)
{
int ret = 0;
for(int i = 0; i < numsSize; i++)
{
ret ^= nums[i];
}
//Find a bit with 1 in ret
int j = 0;
for(; j < 32; ++j)
{
if(ret & (1<<j)) // if(ret>>j & 1)y
{
break;
}
// The j-th bit of ret is 1, indicating that the j-th bits of X and y are 1 and 0
}
// The original array is divided into two groups, a group with bit j as 1 and a group with bit j as 0
//X and y will enter group a and group b respectively. Other numbers that appear twice will either enter group a or group b
//The data of group a and group b will be changed into other numbers, which will appear twice, and only one number will appear once, and then XOR respectively
int x = 0;
int y = 0;
for(int k = 0; k < numsSize; ++k)
{
if(nums[k] & (1<<j)) //Group a
{
x ^= nums[k];
}
else //Group b
{
y ^= nums[k];
}
}
int* arr = (int*)malloc(sizeof(int)*2);
arr[0] = x;
arr[1] = y;
*returnSize = 2;//Output type parameter, let the outside get the array length
return arr;
}
Note: the more strict compiler does not allow the 1 of int to shift 31 bits to the left, because it will run to the symbol bit
You can consider moving to the right
Or cast to another type, long long or unsigned int
Sword finger Offer II 004 A number that appears only once
Give you an integer array nums. Except that an element appears only once, every other element appears * * three times** Please find and return the element that appears only once.

int singleNumber(int* nums, int numsSize)
{
unsigned int arr[32] = {0};
//int is the highest signed bit, and the valid data is only 31 bits
//After changing to unsigned, all bits are data bits
int count = 0;
int k = 31;
for(int i = 0;i < 32;i++)
{
for(int j = 0;j < numsSize;j++)
{
count += ((nums[j]>>i) & 1);
}
arr[k] = count;
count = 0;
k--;
}
for(int i = 0;i < 32;i++)
{
arr[i] %= 3;
}
int ret = 0;
for(int i = 0;i < 32;i++)
{
ret |=(arr[31-i]<<i); //Compilation failed on Leetcode here
}
return ret;
}
Idea:
Since the number of other numbers is odd this time, all XOR together cannot eliminate the remaining numbers. So we have to change the way.
Add up each binary bit of all the numbers in the array into an array, and then%3, the final number is the number that appears only once.
Since other numbers appear three times, their binary bit must be a multiple of 3.% 3 is equivalent to subtracting all the repeated bits, and the remaining binary bits are the binary bits of numbers that appear only once.
Steps:
First, use bitwise and to take out each binary bit and add it into the array
Then all the numbers in the array are% 3
Operate the numbers in the array on ret by bitwise OR
//int is the highest signed bit, and the valid data is only 31 bits //After changing to unsigned, all bits are data bits
//Write together succinctly
int singleNumber(int *nums, int numsSize) {
int ans = 0;
for (int i = 0; i < 32; ++i) {
int total = 0;
for (int j = 0; j < numsSize; ++j) {
total += ((nums[j] >> i) & 1);
}
if (total % 3) {
ans |= (1u << i);
}
}
return ans;
}
Binary search
Best: O(1)
Binary search is also called half search
In terms of time complexity, it is used to be abbreviated as logN
Some data will be written as lgN. Strictly speaking, this is wrong. It is confused with mathematics
Binary search requires data to be sorted first
You can use qsort to sort quickly
Sort first – > binary search
qsort time complexity N* logN
Binary search logN
After sorting, the binary search is fast and convenient for multiple searches

The red black tree / hash table is the real algorithm for searching
recursive algorithm
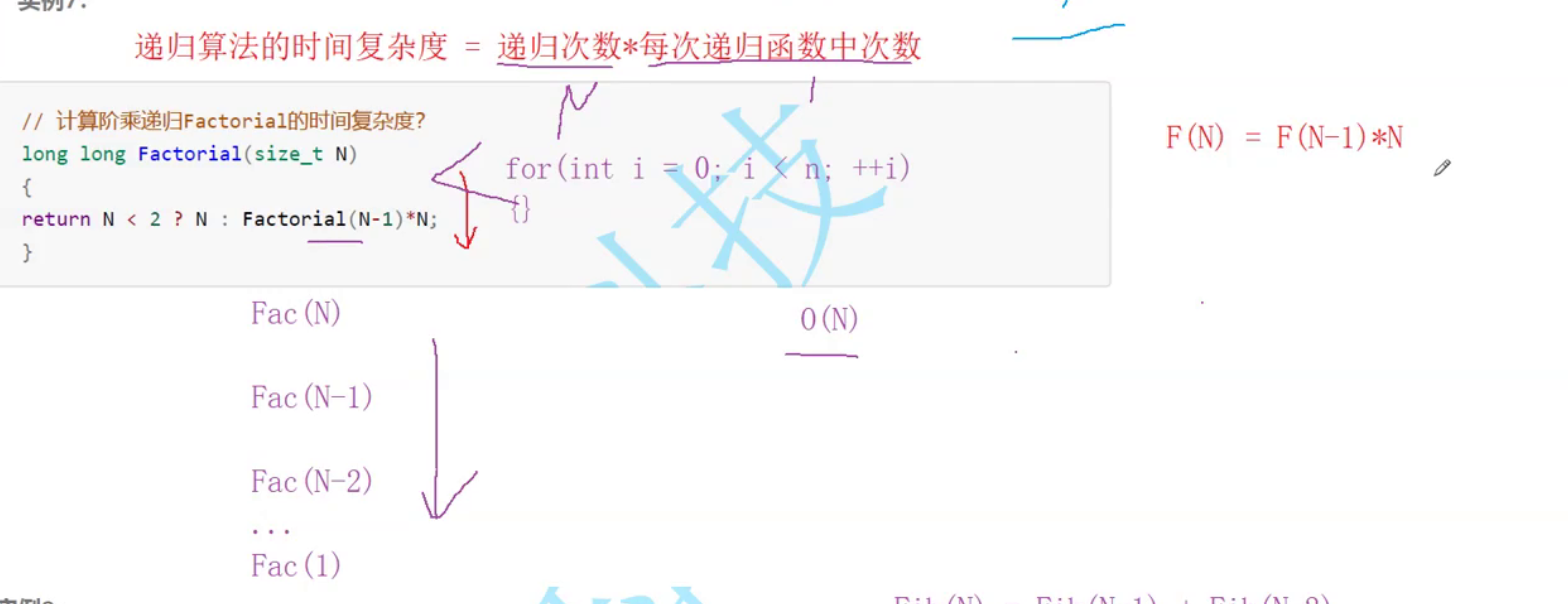
Time complexity of recursive algorithm = number of recursions * number of times in each recursive function
Fac(N)–>Fac(N-1)–>...Fac(1)
That is, N*1(1 represents constant times)
Time complexity O(N)
If another for loop is set, it is O(N^2)
Fibonacci sequence
Note that the Fib completed in advance needs to be subtracted, which can be ignored
You can estimate the CPU operating efficiency, which is generally 100 million
2 ^ 30 is about 1 billion
#include<time.h>
long long Fibonacci(size_t N)
{
return N < 2 ? N : Fibonacci(N - 1) + Fibonacci(N - 2);
}
int main()
{
int begin = clock();
Fibonacci(40);
int end = clock();
printf("%d\n", end - begin);
}
/*
40 Calculate 3339ms,45 calculate 36351ms
The time complexity of this algorithm is too high, which is meaningless in practice
O(2^N)
Consider changing to cycle -- > O (n)
*/

#include<stdio.h>
//Complexity O(N)
int fib(int n)
{
int a = 1;
int b = 1;
int c = 1;//n = 1/2 return directly to 1 without going through the cycle
while (n > 2)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d\n", ret);
return 0;
}
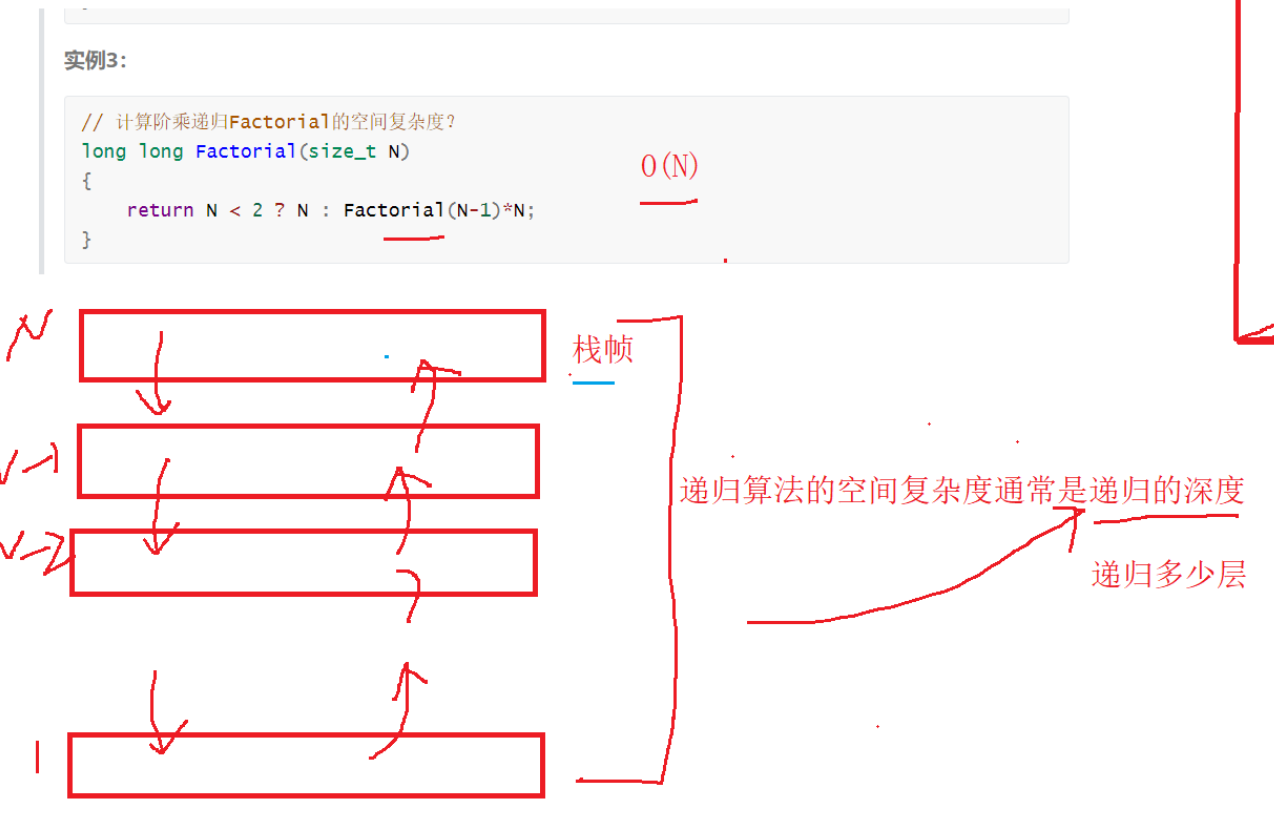
Spatial complexity
With the development of technology, the requirements for space are relatively low, and we don't pay much attention to the complexity of space
Space complexity is not to calculate how many bytes the program occupies
It's the number of variables
Bubble sorting
Bubble sort space complexity O(1) - constant space
The input number is not considered, but the extra space in the operation of the algorithm is considered
Time is cumulative, space is not cumulative, and space can be reused
The space was used for the first time. After the destruction, the space was used for the next time
Fibonacci

Open n+1 space is O(N)
The complexity is not considered for a call, but for the algorithm
recursion
Each call creates a function stack frame
There is a constant space in each stack frame