Computational Intelligence-K-means Clustering Algorithms Learning

Definition

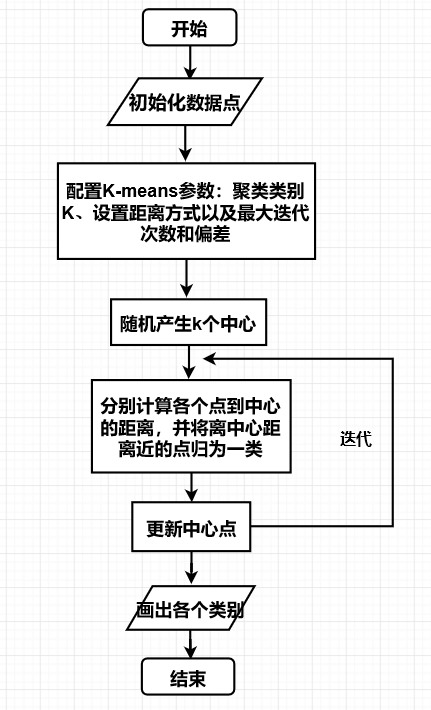
k-means clustering algorithm is an iterative clustering analysis algorithm. Its step is to randomly select K objects as the initial clustering center, then calculate the distance between each object and each seed clustering center, and assign each object to the nearest clustering center.

algorithm

1. Random finding of the center points of k classes in lattice
2. Calculate the distances between some points in the lattice and the central points, and classify the points according to the distances.
3. Find the right center point after classification and iterate several times.

Note: 1. Avoid randomly generating scatter points in the whole space, and try to generate random scatter points around some points as far as possible.
2. There can be multiple classes

algorithm flow chart

code implementation

clear
clc
%%Input data
%First, enter the data, where the mean is used.+variance*The initial lattice is constructed by random matrix to avoid the lattice being too scattered, and then the outliers in the data are judged.
data1 = 0.05 + sqrt(0.01) * randn(20,2)
data2 = 0.6 + sqrt(0.01) * randn(15,2)
data3 = 0.9 + sqrt(0.01) * randn(10,2)
data = [data1;data2;data3]
figure(1)
plot(data(:,1),data(:,2),'*') 
%%Determine whether the data contains incorrect data or illegal characters
isNAN = any(isnan(data),2); 
 %any Expressing right or wrong0When the element is returned as1,any(A,2)Judgment of row vectors representing matrices
hadNAN=any(isNAN);          %Represents bad data in data
if hadNAN
    disp('kmeans:MissingDataRemoved');
    disp(['missaddress is located ' num2str(find(isNAN==1))])
    data = data(~isNAN,:);
end
%%Setting Cluster Categories k
k=3;
%To configureK-means Parameters, including clustering categoriesK,Set the distance mode and the maximum number of iterations and deviations.
%%Setting Distance Mode
%Distance selection
%European distance:'euclidean'，Standard European Distance:'seuclidean'
%Manhattan Distance(Distance between urban blocks): 'cityblock'
%Minkowski Distance:'minkowski'
%Chebyshev Distance:'chebychev'
%Included angle cosine distance:'cosine'
%Relevant distance:'correlation'
%Hanming Distance:'hamming'
distanceSize='euclidean'; 
%%Set the maximum number of iterations step And deviation
step=10;
maxdeviation=1e-5;

%start kmeans clustering
[m,n]=size(data);         %Number of data m The dimension of the dimension is ___________. n dimension
center = zeros(k,n+1);    %Clustering center
center(:,n+1) =1:k ;      %Generating Clustering Categories
dataSize=zeros(m,1);      %Generate data categories
for j=1:k
    center(j,1:n)=data(randi([1,m]),:);  %Random production k Center
end
  for i=1:step
    %%In the second step, the distances from each point to the center are calculated separately, and the points close to the center are grouped into one group.
    %Calculated distance
    for j=1:k
        distance(:,j)=pdist2(data,center(j,1:n),distanceSize);
    end
    %Categorize the points with the smallest distance into one class
    [~,temp]=min(distance,[],2);
    dataSize=temp;
    oldcenter=center;
    %%Update Center Point
    for j=1:k
        center(j,1:n)=mean(data(dataSize==j,:));
    end
    deviation=sum(abs(center-oldcenter));  %residual
    if deviation<maxdeviation
        break;
    end
    %Output of each iteration
    figure(i+10)
    for i=1:k
        scatter(data(dataSize==i,1),data(dataSize==i,2));
    hold on
    end
    plot(center(:,1),center(:,2),'x','MarkerSize',10);
    hold off
    end
    %Draw categories
figure(2)
for i=1:k
    scatter(data(dataSize==i,1),data(dataSize==i,2));
    hold on
end
plot(center(:,1),center(:,2),'x','MarkerSize',10);
hold off

Operation result

Initial lattice: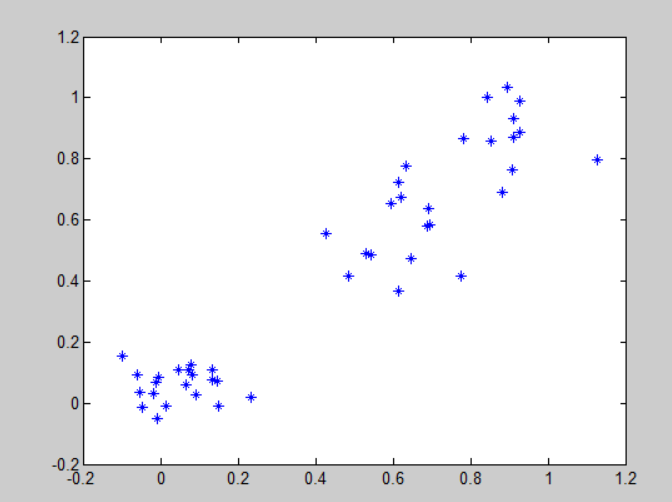

After clustering,

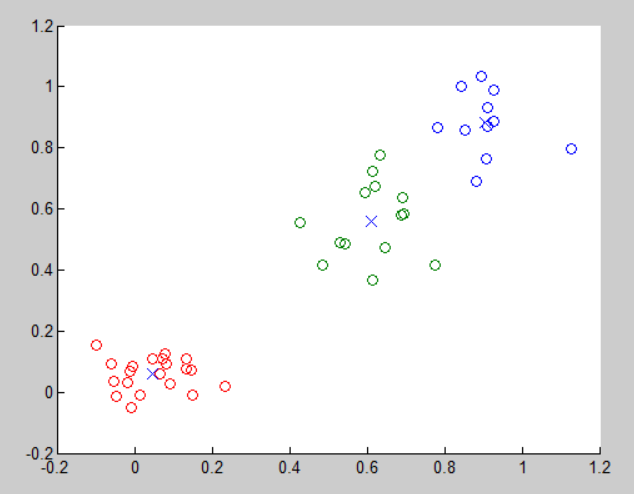
Advantages and disadvantages of k-means algorithm

K-means has the following advantages:
(1) The algorithm is simple, especially for spherical distribution data.
(2) The convergence speed is fast, and it usually takes only 5-6 steps to achieve convergence.
(3) The complexity of the algorithm is O(t,k,n). Among them, t is the number of iterations, K is the number of classifications, and N is the number of data points.
Of course, K-means has some drawbacks.
(1) Because the clustering algorithm is unsupervised learning, people can not determine in advance how many clusters need to be divided, that is to say, k value can not be determined in advance.
(2) Like many algorithms, it may converge to the local optimal solution. This is related to the selection of the initial point. We can select the initial point many times and finally choose the best result.
(3) Sensitive to noise. We can see that the mean in K-means is the average value, and the average value is often sensitive to noise. An outlier often has a great impact on the whole result.
(4) It is not suitable for some aspheric data distribution.

Reference resources

https://blog.csdn.net/u010936286/article/details/79995982