Bibliography: data structure course (Fifth Edition), edited by Li Chunbao
Computer experiment of data structure (Chapter II) I

Time complexity:

	Find elements with sequence number i(1 ≤ i ≤ n)	Find the first element with a value of x	Insert a new element as the first element	Insert the new element as the last element	Insert the i(2 ≤ i ≤ n) th element	Delete first element	Delete last element	Delete the i(2 ≤ i ≤ n) th element
Sequence table	O(1)	O(n)	O(n)	O(1)	O(n)	O(n)	O(1)	O(n)
Single linked list of leading nodes	O(n)	O(n)	O(1)	O(n)	O(n)	O(1)	O(n)	O(n)
Cyclic single linked list of leading nodes	O(n)	O(n)	O(1)	O(n)	O(n)	O(1)	O(n)	O(n)
Circular single linked list with no leading node and only tail node pointer identification	O(n)	O(n)	O(1)	O(1)	O(n)	O(1)	O(n)	O(n)
Double linked list of leading nodes	O(n)	O(n)	O(1)	O(n)	O(n)	O(1)	O(n)	O(n)
Cyclic double linked list of leading nodes	O(n)	O(n)	O(1)	O(1)	O(n)	O(1)	O(1)	O(n)

1. A linear table ( a 1 , a 2 , ... , a n ) ( n > 3 ) (a_1,a_2,...,a_n)(n>3) (a1, a2,..., an) (n > 3) use the single linked list L of the leading node to store and find the element at the middle position (i.e. the serial number is L [ n 2 ] L[\frac{n}{2}] L[2n]).

ElemType MidEle(LinkList &L)
{
	LNode* p = L->next, * q = p;
	while (p->next != NULL && p->next->next != NULL)
	{
		q = q->next; //q move back one node at a time
		p = p->next->next; //p move back two nodes at a time
	}
	return q->data; //Data field returned q
}

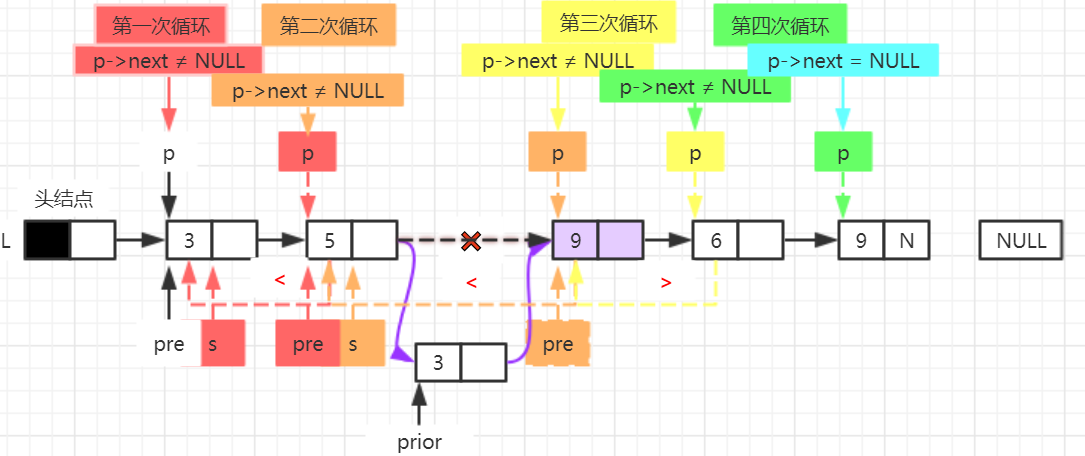
2. Insert a node with a value of x before the first maximum node (there may be multiple maximum nodes) in the non empty single linked list L of the leading node.

void InsertEle(LinkList &L,int x)
{
	LNode* p = L->next, * pre = p, * s, * prior;
	while (p->next != NULL)
	{
		p = p->next;
		if (p->data > pre->data)
		{
			s = pre;
			pre = p;
		}
	}
	prior = (LNode*)malloc(sizeof(LNode)); //Open up a new node space
	prior->data = x; //The data field is x
	prior->next = s->next; //insert
	s->next = prior;
}

Program analysis:

• Operation results:
  
• Time complexity: O(n); Space complexity: O(1)

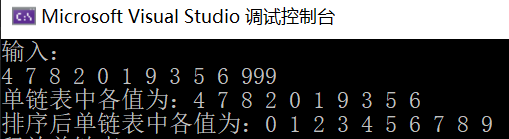
3. Output the data elements of each node in the single linked list in descending order, and then release the storage space occupied by all nodes, and the space complexity of the algorithm is required to be O(1).

• Algorithm idea: refer to question 3 of computer experiment (Chapter 2) I in data structure.

void SortEle(LinkList &L)
{
	LNode* p = L->next->next, * s, * num;
	L->next->next = NULL;
	while (p != NULL)
	{
		num = L;
		s = p;
		p = p->next;
		while (num->next != NULL && s->data > num->next->data)
			num = num->next;
		s->next = num->next;
		num->next = s;	
	}
}

void DestoryList(LinkList& L) //Destroy single linked list
{
	LNode* pre = L, * p = L->next; //pre points to the precursor node of node p
	while (p != NULL) //Scan single linked list L
	{
		free(pre); //Release free node 
		pre = p; //Move one node after pre and p synchronization
		p = pre->next;
	}
	free(pre); //At the end of the loop, p is NULL, pre points to the tail node and releases it
}

void fun(LinkList& L)
{
	printf("The values in the single linked list are:");
	PrintList(L);
	printf("\n");
	SortEle(L);
	printf("The values in the sorted single linked list are:");
	PrintList(L);
	printf("\n");
	printf("Release single linked list:");
	DestoryList(L);
}

Program analysis:

• Operation results:
  
• Time complexity: Ｏ ( n 2 ) Ｏ(n^2) Ｏ(n2)； Space complexity: O ( 1 ) O(1) O(1)

4. There is a double linked list h. in each node, in addition to the fields of prior, data and next, there is also an access frequency field freq. before the linked list is enabled, its values are initialized to zero. Whenever the Locatenode(h,x) operation is performed, the value of the freq field in the node whose element value is x is increased by 1, and the order of the nodes in the table is adjusted to arrange them in descending order of access frequency, so that the frequently accessed nodes are always close to the header.

• Algorithm idea: add an integer freq field in the definition of DNode type and initialize the field to 0. Each time a node p is found, its freq field is increased by 1, and then compared with the previous node pre. If the freq field value of the node is large, the two are exchanged.

bool LocateNode(DLinkList h, ElemType x)
{
	DNode* p = h->next, * pre;
	while (p != NULL && p->data != x)
		p = p->next; //Find node p with data field value of x
	if (p == NULL) return false; //Conditions not found
	else //Find the situation
	{
		p->freq++; //Frequency + 1
		pre = p->prior; //Node pre is the precursor node of node p
		while (pre != h && p->freq > pre->freq)
		{ //Delete pre node
			p->prior = pre->prior;
			pre->prior->next = p;
			//Insert the pre node after the p node
			pre->next = p->next;
			if (pre->next != NULL) //If p is not the tail node
				p->next->prior = pre;
			pre->prior = p;
			p->next = pre;
			//q points to the precursor node of node p
			pre = p->prior;
		}
		return true;
	}
}
LocateNode(h, 5);

Program analysis:

• Operation results:
  
• Time complexity: Ｏ ( n ) Ｏ(n) Ｏ(n)； Space complexity: O ( 1 ) O(1) O(1)

5. Design h a = ( a 1 , a 2 , ... , a n ) ha=(a_1,a_2,...,a_n) ha=(a1, a2,..., an) and h b = ( b 1 , b 2 , ... , b n ) hb=(b_1,b_2,...,b_n) hb=(b1, b2,..., bn) is the circular single linked list of two leading nodes. These two tables are combined into the circular single linked list hc of the leading node.

• Algorithm idea: first find the tail node P of ha, point the next of node p to the first node of hb, and then find the tail node P of hb to form a circular single linked list.

void ConList(LinkList &ha, LinkList &hb)
{
	LNode* pa = ha->next, * pb = hb->next;
	while (pa->next != ha)
		pa = pa->next;
	pa->next = pb;
	while (pb->next != hb)
		pb = pb->next;
	pb->next = ha;
}
ConList(ha,hb);

Program analysis:

• Operation results:
  
• Time complexity: Ｏ ( l e n g t h ( h a ) ) + O ( l e n g t h ( h b ) ) Ｏ(length(ha))+O(length(hb)) Ｏ(length(ha))+O(length(hb))； Space complexity: O ( 1 ) O(1) O(1)

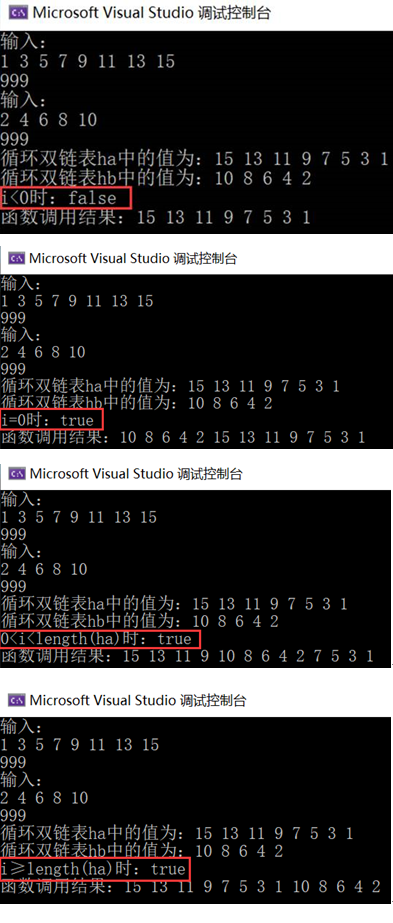
6. Let two non empty linear tables be represented by the cyclic double linked list HA and hb of the leading node respectively, and design an algorithm Insert(ha,hb,i). Its function is to insert hb in front of HA when i=0; When i > 0, insert hb after the ith node in HA; When i is greater than or equal to the length of HA, insert hb after ha.

void hbhaList(DLinkList ha, DLinkList hb)
{
	DNode* pa = ha->next, * pb = hb->next;
	pb->prior = ha;
	ha->next = pb;
	hb->prior->next = pa;
	pa->prior = hb->prior;
}

void insertList(DLinkList& ha, DLinkList& hb,int i)
{
	DNode* pa = ha->next, * pb = hb->next;
	int j = 1;
	while (pa != ha && j < i)
	{
		j++;
		pa = pa->next;
	}
	hb->prior->next = pa->next;
	pa->next = hb->prior;
	pb->prior = pa;
	pa->next = pb;
}

void hahbList(DLinkList ha, DLinkList hb)
{
	DNode* pa = ha->next, * pb = hb->next;
	ha->prior->next = pb;
	pb->prior = ha->prior;
	hb->prior->next = ha;
	ha->prior = hb->prior;
}

bool Insert(DLinkList& ha, DLinkList& hb, int i)
{
	if (i < 0) return false;
	else if (i == 0) hbhaList(ha, hb);
	else if (i > 0 && i < DListLength(ha)) insertList(ha, hb,i);
	else  if (i >= DListLength(ha)) hahbList(ha, hb);
	return true;
}

①Insert(ha, hb, -3);
②Insert(ha, hb, 0);
③Insert(ha, hb, 4);
④Insert(ha, hb, 10);

Program analysis:

• letter number transfer use = { f a l s e , i<0 t r u e { h b insert enter reach h a of front noodles , i=0 h b insert enter reach h a in The first i individual junction spot of after noodles , 0<i<length(ha) h b insert enter reach h a of after noodles , i≥length(ha) Function call = \ begin {cases} false, & \ text {i < 0} \ \ true \ begin {cases} HB inserted in front of HA, & \ text {i = 0} \ \ HB inserted behind the ith node in ha, & \ text {0 < i < length (HA)} \ \ HB inserted behind ha, & \ text {i ≥ length (HA)} \ \ end {cases} Function call = ⎩⎪⎪⎪⎨⎪⎪⎪⎧ false,true ⎩⎪⎨⎧ hb is inserted in front of HA, hb is inserted behind the ith node in ha, hb is inserted behind ha, i = 00 < i < length(ha) i ≥ length(ha) i < 0
• Operation results:
  

7. Use the single linked list of the leading node to represent the integer set, complete the following algorithm and analyze the time complexity:

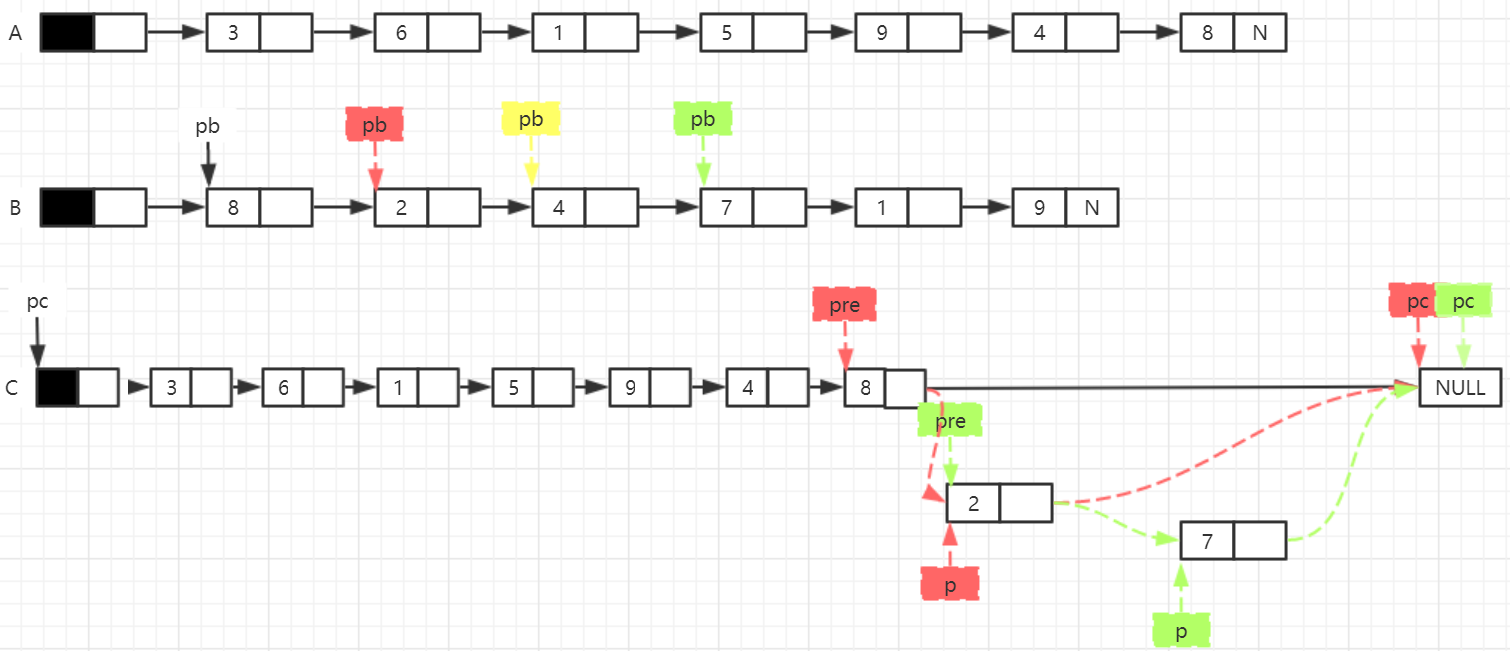
(1) The union operation of two sets A and B, i.e. C=AUB, is required not to destroy the original single linked tables A and B.

• Algorithm idea: sets A, B and C are stored in single linked lists ha, hb and hc respectively. The tail interpolation method is used to create the single linked list hc. First copy all the nodes in the HA single linked list into hc, then scan the single linked list hb and copy all the nodes that do not belong to ha into hc.

void Union1(LinkList LA, LinkList LB, LinkList LC)
{
	LNode* pa = LA->next, * pb = LB->next, * pc = LC, * p, * pre;
	while (pa != NULL)
	{
		p = (LNode*)malloc(sizeof(LNode));
		p->data = pa->data;
		p->next = pc->next;
		pc->next = p;
		pc = pc->next;
		pa = pa->next;
	}
	pc = LC->next;
	while (pb != NULL)
	{
		while (pc != NULL && pb->data != pc->data)
		{ 
			pre = p;
			pc = pc->next;
		}
		if (pc == NULL)
		{
			p = (LNode*)malloc(sizeof(LNode));
			p->data = pb->data;
			p->next = pc;
			pre->next = p;
		}
		pc = LC->next;
		pb = pb->next;
	}
}

Program analysis:

• Operation results:
• Time complexity: O(m) × n) Where m and N are the number of data nodes in the single linked tables LA and LB; Spatial complexity: O(m+n).

(2) Assuming that the elements in the set are arranged incrementally, the union operation of two sets A and B, that is, C=AUB, is required not to destroy the original single linked lists A and B.

Algorithm idea: the tail interpolation method is also used to create a single linked list hc, and the order of the single linked list is used to improve the efficiency of the algorithm.

void Union2(LinkList LA, LinkList LB, LinkList LC)
{
	LNode* pa = LA->next, * pb = LB->next, *pc,* rc=LC;
	while (pa != NULL && pb != NULL)
	{
		if (pa->data < pb->data) //Copy the smaller node pa to the pc
		{
			pc = (LNode*)malloc(sizeof(LNode));
			pc->data = pa->data;
			pc->next = rc->next;
			rc->next = pc;
			pa = pa->next;
			rc = rc->next;
		}
		else if (pa->data > pb->data) //Let the smaller nodes pb copy to the pc
		{
			pc = (LNode*)malloc(sizeof(LNode));
			pc->data = pb->data;
			pc->next = rc->next;
			rc->next = pc;
			pb = pb->next;
			rc = rc->next;
		}
		else //Equal nodes are copied only once
		{
			pc = (LNode*)malloc(sizeof(LNode));
			pc->data = pa->data;
			pc->next = rc->next;
			rc->next = pc;
			pa = pa->next;
			pb = pb->next;
			rc = rc->next;
		}
	}
	if (pb != NULL) pa = pb; //Let pa point to the single linked list node that has not been scanned
	while(pa!=NULL)
	{
		pc = (LNode*)malloc(sizeof(LNode));
		pc->data = pa->data;
		pc->next = rc->next;
		rc->next = pc;
		pa = pa->next;
		rc = rc->next;
	}
}

Program analysis:

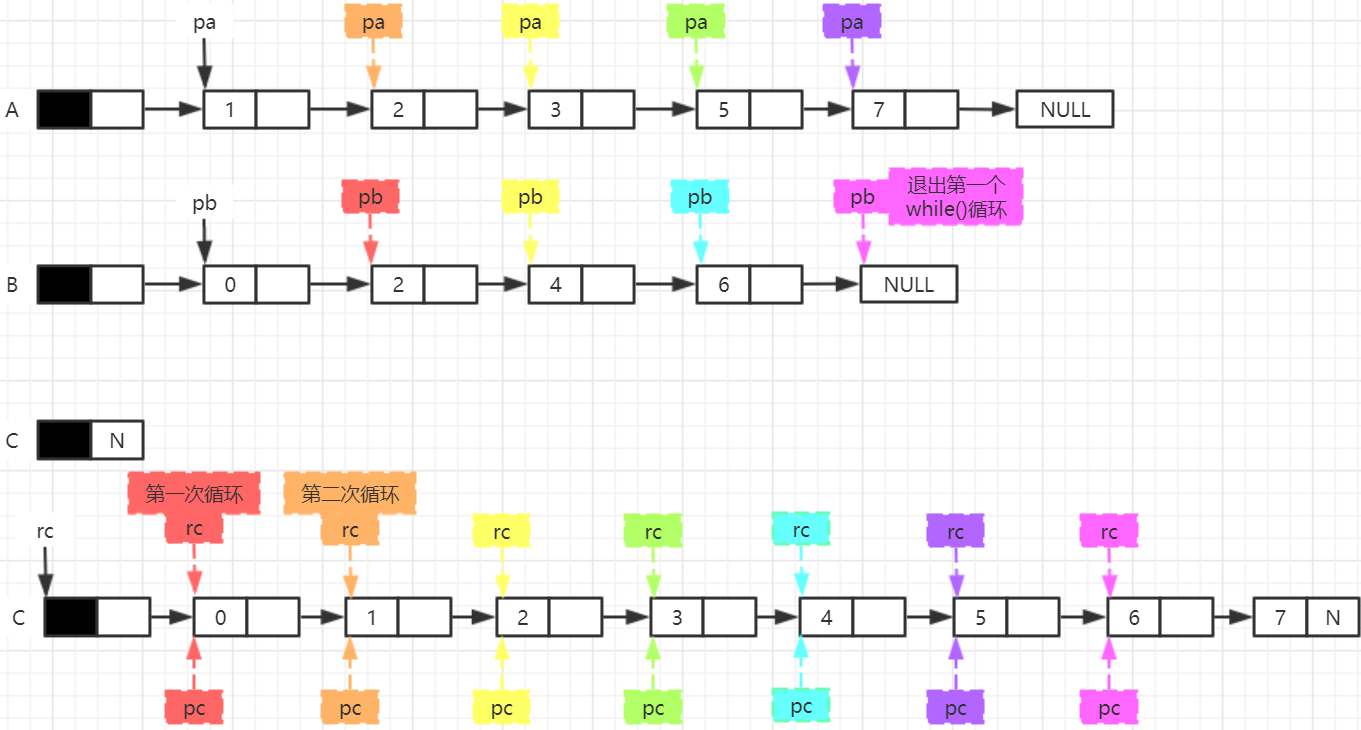
• Operation results:
  
• Time complexity: O(m+n), where m and N are the number of data nodes in the single linked list LA and LB; Spatial complexity: O(m+n).

8. Use the single linked list of the leading node to represent the integer set, complete the following algorithm and analyze the time complexity:

(1) Find the intersection operation of two sets A and B (C=A ∩ B), that is, the elements in both A and B.

• Algorithm idea: refer to question 7

void InterSect(LinkList &L1, LinkList &L2)
{
	LNode* pa = L1->next, * pb = L2->next, * s1 = L1, * s2 = L2, * prea, * preb;
	while (pa != NULL)
	{
		while (pb != NULL && pb->data != pa->data)
			pb = pb->next;
		if (pb == NULL)
		{
			prea = pa;
			pa = pa->next;
			s1->next = pa;
			free(prea);
		}
		else
		{
			s1 = pa;
			pa = pa->next;
		}
		pb = L2->next;
	}
}

Program analysis:

• Operation results:
• Time complexity: O(m) × n) Where m and N are the number of data nodes in the single linked tables LA and LB; Space complexity: O(1).

(2) Assuming that the elements in the set are arranged incrementally, the intersection operation of two sets A and B (C=A ∩ B) is obtained, that is, the elements in both A and B.

void InterSect(LinkList &L1, LinkList &L2)
{
	LNode* pa = L1->next, * pb = L2->next, * s1 = L1, * s2 = L2, * prea, * preb;
	while (pa != NULL && pb != NULL)
	{
		if (pa->data == pb->data)
		{
			s1 = pa;
			pa = pa->next;
			preb = pb;
			pb = pb->next;
			s2->next = pb;
			free(preb);
		}
		else if (pa->data < pb->data)
		{
			prea = pa;
			pa = pa->next;
			s1->next = pa;
			free(prea);
		}
		else
		{
			preb = pb;
			pb = pb->next;
			s2->next = pb;
			free(preb);
		}	
	}
	if (pb == NULL) s1->next = NULL;
	free(pa);
}

• Operation results:
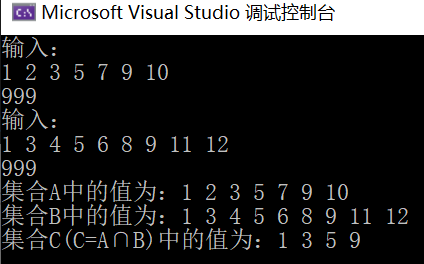
• Time complexity: O(m+n), where m and N are the number of data nodes in the single linked list LA and LB; Space complexity: O(1).

9. Use the single linked list of the leading node to represent the integer set, complete the following algorithm and analyze the time complexity:

(1) Find the difference set operation of two sets A and B (C=A-B), that is, the elements in A and not in B. The space complexity of the algorithm is O(1), and the unnecessary nodes in single linked lists A and B are released.

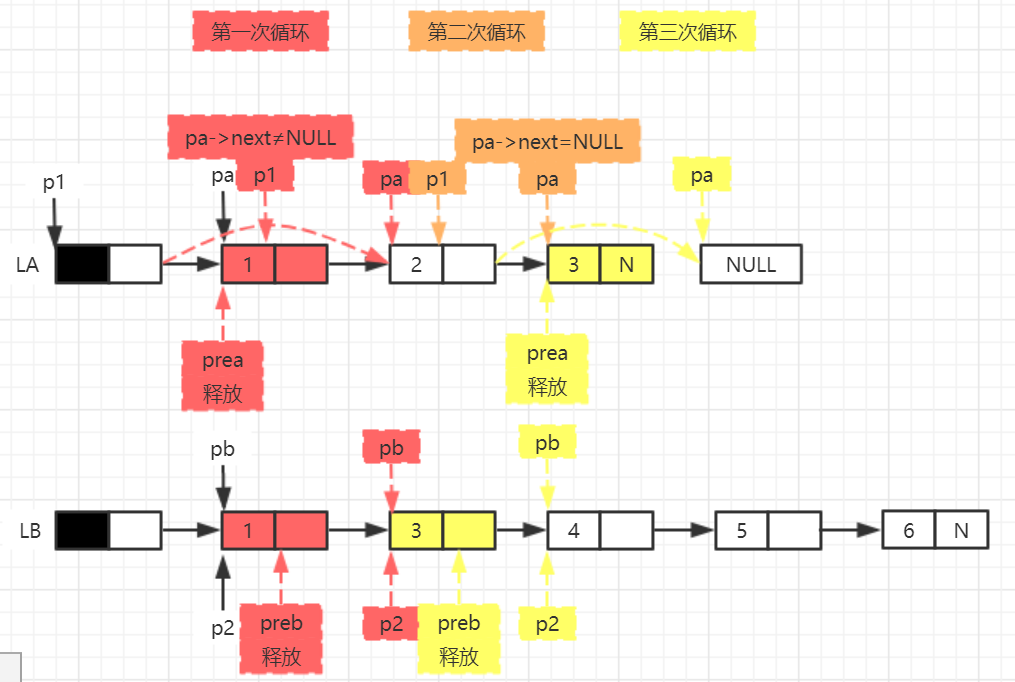
Sets A, B and C are stored in single linked tables LA, LB and LC respectively. Because the space complexity is required to be O(1), the replication method can not be used. Only the node reorganization in the original single linked list can be used to produce the resulting single linked list.

• Algorithm idea: delete all nodes in hb in ha single linked list, and then delete all nodes in hb.

void Sub1(LinkList LA, LinkList LB)
{
	LNode* pa = LA->next, * pb = LB->next, * p = LA, * prea, * preb, * r = LB;
	while (pa != NULL)
	{
		while (pb != NULL && pb->data != pa->data) 
			pb = pb->next;
		if (pb == NULL)
		{
			p = p->next;
			pa = pa->next;
		}
		else
		{
			if (pa->next != NULL) p->next = pa->next;
			else p->next = NULL;
			prea = pa;
			pa = pa->next;
			free(prea);
		}
		pb = LB->next;
	}
	while (r != NULL) //Release LB
	{
		preb=r;
		r = r->next;
		free(preb);
	}
}

Program analysis:

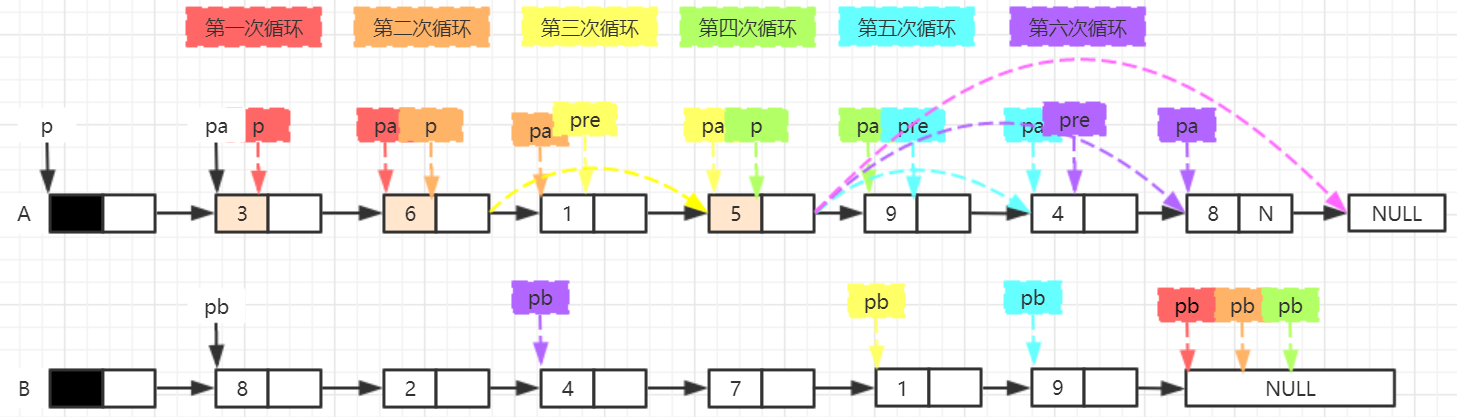
• Operation results:
  
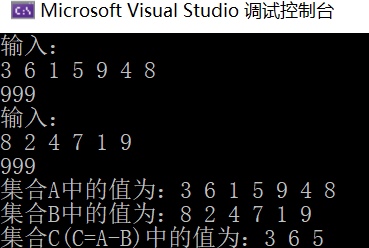
• Time complexity: O(m) × n) Where m and N are the number of data nodes in the single linked tables LA and LB; Space complexity: O(1).

(2) Assuming that the elements in the set are arranged incrementally, an efficient algorithm is designed to calculate the difference set operation of two sets A and B (C=A-B), that is, the elements in A and not in B. The space complexity of the algorithm is O(1), and the unnecessary nodes in single linked lists A and B are released.

• Algorithm idea: the tail interpolation method is also used to create the single linked list LC, and the two-way merging method is used to improve the efficiency of the algorithm by taking advantage of the order of the single linked list. The unnecessary nodes are deleted while comparing.

void Sub2(LinkList LA, LinkList LB)
{
	LNode* pa = LA->next, * pb = LB->next, * p1 = LA, * p2 = LB->next, * prea, * preb;
	while (pa != NULL && pb != NULL)
	{
		if (pa->data < pb->data)
		{
			p1 = p1->next;
			pa = pa->next;
		}
		else if (pa->data > pb->data)
		{
			preb = p2;
			p2 = p2->next;
			pb = pb->next;
			free(preb);
		}
		else
		{
			p1->next = pa->next;
			prea = pa;
			pa = pa->next;
			free(prea);
			preb = p2;
			p2 = p2->next;
			pb = pb->next;
			free(preb);
		}
	}
	free(LB); //Release the head node of LB
}

Program analysis:

• Operation results:
• Time complexity: O(m+n), where m and N are the number of data nodes in the single linked list LA and LB; Space complexity: O(1).

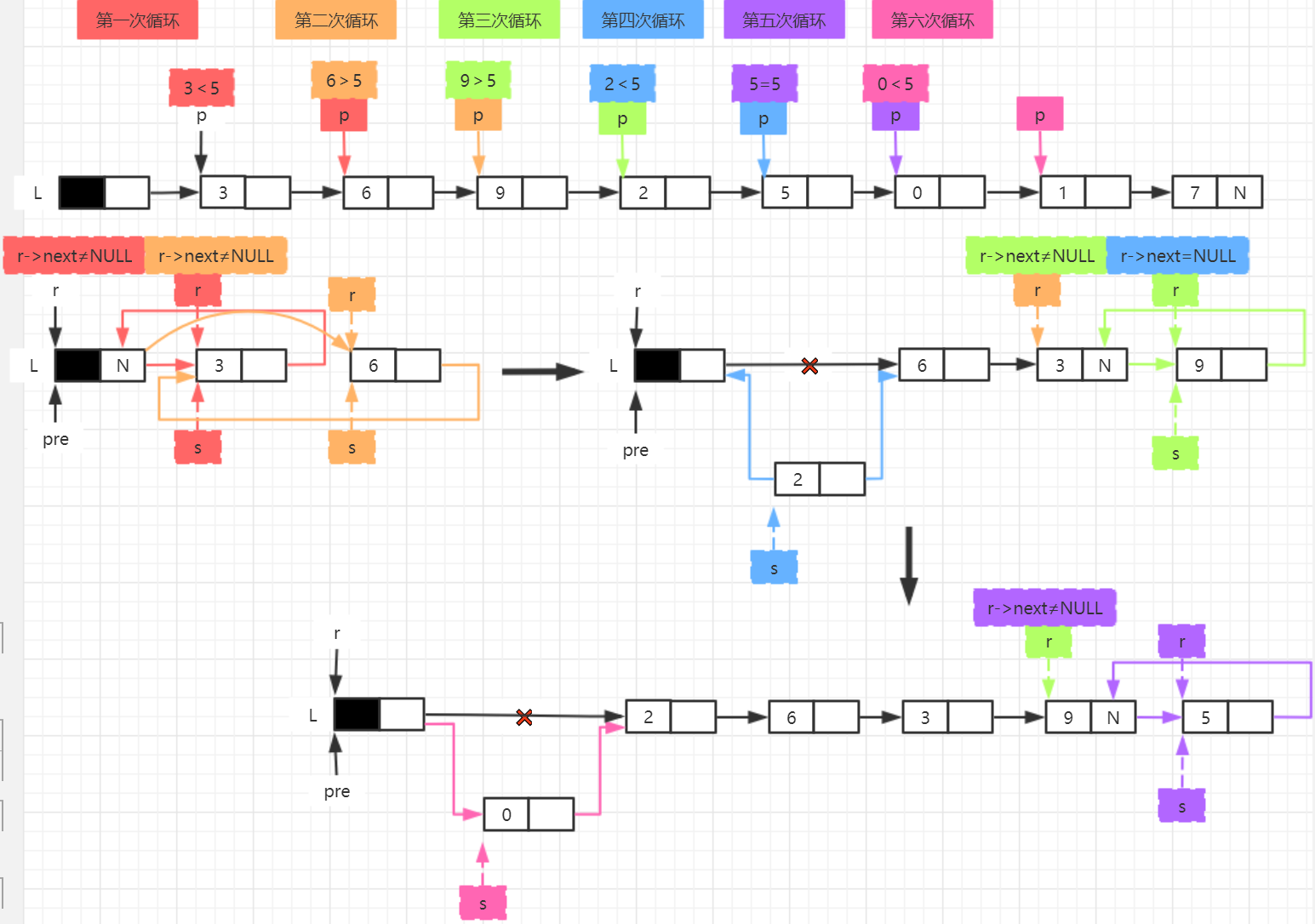
10. Based on the given value x, the single linked list is divided into two parts, and all nodes less than X are arranged before nodes greater than or equal to X.

void Split(LinkList L, int x)
{
	LNode* p = L->next, * s ;
	L->next = NULL; //L becomes an empty linked list
	LNode* pre = L, * r = L; //pre is the head node pointer of the new linked list, and r is the tail node pointer of the new linked list
	while (p != NULL)
	{
		if (p->data >= x) //If the value of p node is less than x, it is inserted at the beginning
		{
			s = p;
			p = p->next;
			s->next = r->next;
			r->next = s;
		}
		else //If the value of p node is greater than or equal to x, insert it to the end
		{
			s = p;
			p = p->next;
			s->next = pre->next;
			pre->next = s;
		}
		if (r->next != NULL) r = r->next;
	}
}
Split(L, 5);

Program analysis:

• Operation results:
  
• Time complexity: O(n); Space complexity: O(1).