Computer experiment of data structure (Chapter III) I

1. Input n (input by the user) numbers within 10, insert them into queue i every time i(0 ≤ i ≤ 9) is input, and finally connect the non empty queues in 10 queues into a chain in the order of queue number from small to large, and output all elements of the chain.

Algorithm idea: establish a queue head pointer array quh and queue tail pointer array qut. quh[i] and qut[j] represent the queue head and tail of queue I (0 ≤ I ≤ 9). First set all their elements to NULL. For the input x, the tail interpolation method is used to link it to the X queue. Then, the nodes in these queues are composed in the order of 0 ~ 9 numbers
For a single linked list without a leading node, the first node pointer is head. Finally, output all node values of the single linked list head and release all nodes.

#include<stdio.h>
#include<malloc.h>
#define MAXQNode 10 / / number of queues
typedef struct QNode
{
	int data;
	struct QNode* next;
};

void Insert(QNode* quh[], QNode* qut[], int x) //Insert x into the corresponding queue
{
	QNode* s;
	s = (QNode*)malloc(sizeof(QNode));
	s->data = x;
	s->next = NULL;
	if (quh[x] == NULL)
	{
		quh[x] = s;
		qut[x] = s;
	}
	else
	{
		qut[x]->next = s;
		qut[x] = s;
	}
}

void Create(QNode* quh[], QNode* qut[]) //Create a queue based on user input
{
	int n, x;
	printf("n:");
	scanf("%d", &n);
	for (int i = 0; i < n; i++)
	{
		do {
			printf("Input No%d number:", i+1);
			scanf("%d", &x);
		} while (x<0||x>10);
		Insert(quh, qut, x);
	}
}

void DestroyList(QNode*& head) //Release single linked list
{
	QNode* pre = head, * p = pre->next;
	while(p!=NULL)
	{
		free(pre);
		pre = p;
		p = p->next;
	}
	free(pre);
}

void DisplayList(QNode* head) //Output all node values of single linked list
{
	printf("\n Output all elements:");
	while (head != NULL)
	{
		printf("%d ", head->data);
		head = head->next;
	}
	printf("\n");
}

QNode* Link(QNode* quh[], QNode* qut[]) //Link non empty queues and output
{
	QNode* head = NULL, * tail; //The head node pointer and tail node pointer of the total linked list
	for (int i = 0; i < MAXQNode; i++) //Scan all queues
		if (quh[i] != NULL) //i queue is not empty
		{
			if(head==NULL) //If queue i is the first non empty queue
			{
				head = quh[i];
				tail = qut[i];
			}
			else //If queue i is not the first non empty queue
			{
				tail->next = quh[i];
				tail = qut[i];
			}
		}
	tail->next = NULL;
	return head;
}

int main()
{
	QNode* head;
	QNode* quh[MAXQNode], * qut[MAXQNode];
	for (int i = 0; i < MAXQNode; i++) quh[i] = qut[i] = NULL;
	Create(quh, qut);
	head = Link(quh, qut);
	DisplayList(head);
	DestroyList(head);
	return 0;
}

Program analysis

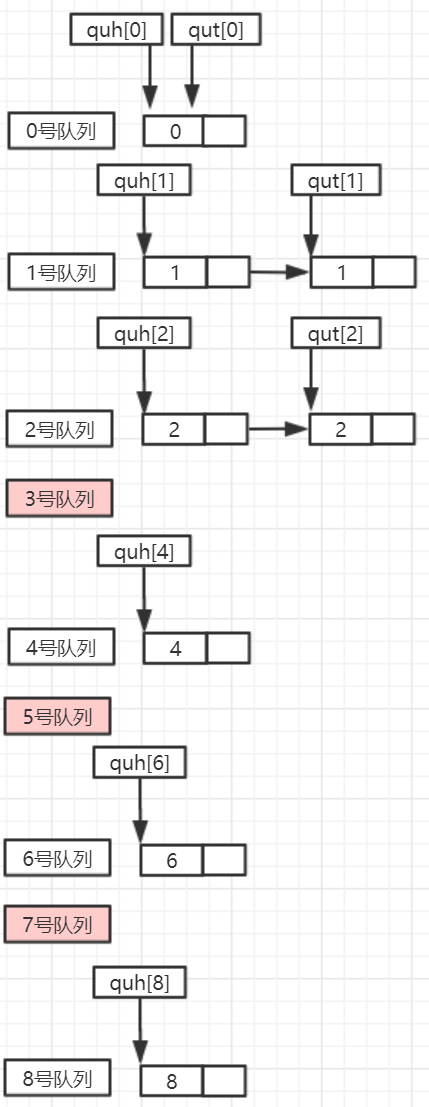
• Operation results:
  
  

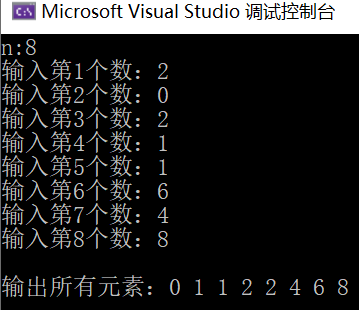
2. Convert a decimal positive integer d to the corresponding binary number

• Algorithmic idea: the Division 2 remainder method is usually used to convert decimal positive integers into binary numbers. In the conversion process, binary numbers are obtained in the order from low to high, which is opposite to the usual order of outputting binary from high to low. Therefore, a stack s is designed to temporarily store the remainder obtained each time. When the conversion process is over, all elements off the stack will get binary numbers from high to low.

void trans()
{
	LinkStNode* s;
	InitStack(s);
	int n, num;
	printf("Enter a positive decimal integer:");
	scanf("%d", &num);
	do {
		Push(s, num % 2);
		num = num / 2;
	} while (num);
	while (!StackEmpty(s))
	{
		Pop(s, n);
		printf("%d", n);
	}
	DestoryStack(s);
}

Program analysis

• Operation results:
  

3. Design an algorithm to output all the elements in the stack from the top to the bottom of the stack by using the basic operation of sequential stack. It is required to keep the elements in the stack unchanged.

• Algorithm idea: first establish and initialize a temporary temp. Withdraw all elements in s, output these elements and put them on the stack to temp, and then take the elements in temp out of the stack one by one and put them on the stack to s, so as to restore the original elements in s stack.

void diverse()
{
	LinkStNode* s, * temp;
	InitStack(s); InitStack(temp);
	int n, num;
	printf("Input:");
	scanf("%d", &num);
	while (num != 999)
	{
		s->data = num;
		Push(s, s->data);
		scanf("%d", &num);
	}
	while (!StackEmpty(s))
	{
		Pop(s, n);
		printf("%d ", n);
		Push(temp, n);
	}
	while (!StackEmpty(temp))
	{
		Pop(temp, n);
		Push(s, n);
	}
	DestoryStack(temp);
}

Program analysis

• ! Note that this problem can only be completed by using the basic operation of the stack, and the elements in the stack cannot be directly output by ST - > data [i].
• Operation results:
  

4. Use the basic operation of sequential stack to find the k-th element from the top to the bottom of the stack. It is required to keep the elements in the stack unchanged.

-Algorithm idea: first establish and initialize a temporary stack temp. Withdraw all elements x in S and use i to accumulate the number of elements. When i==k, put all elements into temp, and then drive the elements in temp out of the temporary stack and into s, so as to restore the original elements in s stack. If there is no k-th element in, false is returned; Otherwise, it returns true.

bool diverse(int k)
{
	LinkStNode* s, * temp;
	InitStack(s); InitStack(temp);
	int n, num;
	printf("Input:");
	scanf("%d", &num);
	while (num != 999)
	{
		s->data = num;
		Push(s, s->data);
		scanf("%d", &num);
	}
	for (int i = 0; i < k; i++)
	{
		Pop(s, s->data);
		
		Push(temp, s->data);
		printf("%d ", s->data);
	}
	if (StackEmpty(s))
	{
		printf("\n The second row does not exist in the stack%d Elements", k);
		return false;
	}
	else
	{
		while (!StackEmpty(temp))
		{
			Pop(temp, n);
			Push(s, n);
		}
		return true;
	}
	DestoryStack(temp);
}

//printf("\n is there the kth element in the stack? -% d", reverse (5));

Program analysis

• ! Note that this problem can only be completed by using the basic operation of the stack. You can't directly use ST - > data [i] to find the element in the k-th stack.
• Operation results:
  

5. There are n(n=5) characters in abcde. A variety of out of stack sequences can be generated through one stack. Judge whether the sequence str is an appropriate out of stack sequence, give the operation process, and test with relevant data.

• Algorithm idea: first establish a character sequence stack s, and store the stack sequence abcde into character array a. Scan arrays a and str with I and j respectively, and their initial values are 0. When the array A and str are not scanned, loop: compare the top elements e and str[j]. If they are different, put A[i] on the stack and add 1 to I; If the two are the same, the stack top elements e and j are added with 1. At the end of the above cycle, all elements of the stack are retreated. If the sequence str is a suitable stack sequence, there must be j==n, otherwise str is not a suitable stack sequence.

bool isSerial(char str[])
{
	LinkStNode* s;
	InitStack(s); 
	char A[MaxSize], e;
	int  i, j = 0, k = 0;
	for (i = 0; i < strlen(str); i++)
		A[i] = 'a'+i;
	while (j < strlen(str) && k < strlen(str))
	{
		if (StackEmpty(s) || (GetTop(s, e) && e != str[k]))
		{
			Push(s, A[j]);
			printf("element%c Enter the stack\n", A[j]);
			j++;
		}
		else
		{
			Pop(s, e);
			printf("element%c Out of stack\n", e);
			k++;
		}
	}
	while (!StackEmpty(s) && (GetTop(s, e)) && e == str[k])
	{
		Pop(s, e);
		printf("element%c Out of stack\n", e);
		k++;
	}
	DestoryStack(s);
	if (k == strlen(str)) return true;
	else return false;
}

void Display(char str[])
{
	for (int i = 0; i < strlen(str); i++)
		printf("%c", str[i]);
}

int main()
{
	char str[6] = { "acbde" };
	Display(str);
	printf("Operation sequence:\n");
	if (isSerial(str))
	{
		Display(str);
		printf("Is the appropriate stack sequence\n");
	}
	else
	{
		Display(str);
		printf("Not a suitable out of stack sequence\n");
	}
	return 0;
}

Program analysis

{ ① Stack s by empty ， A [ i ] element element straight meet enter Stack ② Stack s no by empty ， Obtain take Stack top element element of value ， as fruit Should value And s t r [ j ] of value no mutually etc. ， be take Stack top element element Out Stack \begin{cases} ① stack s is empty, A[i] element is directly put into the stack \ \ ② stack s is not empty, get the value of the top element of the stack. If the value is not equal to the value of str[j], then put the top element out of the stack \ \ end{cases} {① stack s is empty, and A[i] element is directly put into the stack ② stack s is not empty, get the value of the top element of the stack. If the value is not equal to the value of str[j], put the top element out of the stack

• Operation results:
  

6. Using the basic operation of ring queue to return the tail element in the specified queue, the spatial complexity of the algorithm is required to be O(1).

• Algorithm idea: first find the number of elements count in queue q, cycle count times, get an element num out of the queue, and then enter the element num into the queue. The last num is the end of the queue element.

ElemType Last(CyQueue& q)
{
	ElemType num;
	int count = (q.rear - q.front + MaxSize) % MaxSize;
	for (int i = 0; i < count; i++)
	{
		deQueue(q, num);
		enQueue(q, num);
	}
	return num;
}

Program analysis

• Because the algorithm requires a space complexity of O(1), temporary queues cannot be used.
• Operation results:
  

7. Algorithm for deleting the k-th element from the queue head in the queue.

• Algorithm idea: first find the number of elements count in queue q. if K is less than 0 or greater than count, return false. All elements out of the queue, and record the element serial number i. When i=k, the corresponding elements only go out but not in, otherwise the elements out of the queue will go into the queue again.

bool Delete(CyQueue& q, int k)
{
	ElemType num;
	int count = (q.rear - q.front + MaxSize) % MaxSize;
	if (k<0 || k>count) return false;
	for (int i = 0; i < count; i++)
	{
		deQueue(q, num);
		if (i != k) enQueue(q, num);
	}
	return true;
}

Program analysis

• Operation results:
  

8. Suppose there is an integer array to store the scores of n students, and the scores are divided into 3 levels. Those with scores higher than or equal to 90 are Grade A, those with scores lower than 60 are grade C, and others are grade B. It is required to use double ended queue, first output grade a score, then output grade C score, and finally output grade B score.

• Algorithm idea: design deQueue1 from the head of the queue, enQueue1 from the head of the queue and enQueue2 from the tail of the queue. For array a with n fractions, scan all elements a[i]. If a[i] is a, etc., output directly; If it is class B, enter it from the end of the team; If it is a class C, enter it from the head of the team. Finally, get out of the team from the team head and output all elements.

bool enQueue1(DQueue& q, ElemType e) //Join the team from the head of the team
{
	if ((q.rear + 1) % MaxSize == q.front) return false; //Team full
	q.data[q.front] = e; //e element join the team
	q.front = (q.front -1+ MaxSize) % MaxSize; //Modify queue head pointer
	return true;
}

bool enQueue2(DQueue& q, ElemType e) //From the end of the queue into the queue algorithm
{
	if ((q.rear + 1) % MaxSize == q.front) return false; //Team full
	q.rear = (q.rear + 1) % MaxSize; //Modify end of queue pointer
	q.data[q.rear] = e; //e element join the team
	return true;
}

bool deQueue1(DQueue& q, ElemType &e) //Get out of the team
{
	if (q.rear == q.front) return false; //Team air
	q.front = (q.front + 1) % MaxSize; //Modify queue head pointer
	e = q.data[q.front];
	return true;
}

void fun(int a[], int n)
{
	ElemType e;
	DQueue q;
	InitQueue(q);
	for(int i=0;i<n;i++)
	{
		if (a[i] >= 90) printf("%d ", a[i]);
		else if (a[i] >= 60) enQueue2(q, a[i]); //Enter the team from the end of the team
		else enQueue1(q, a[i]); //Enter the team from the head of the team
	 }
	while (!EmptyQueue(q))
	{
		deQueue1(q, e); //Get out of the team
		printf("%d ", e);
	}
	printf("\n");
}

Program analysis

• Operation results:
  

9. The railway transition network for train marshalling is a stack structure, in which the right track is the input end and the left track is the output end. When the car number sequence on the right track is 1, 2, 3 and 4, if the operation is performed into stack, into stack, out of stack, in stack, in stack, out of stack, out of stack and out of stack, the car number sequence on the left track is 2, 4, 3 and 1.

Design an algorithm, input n integers to represent the number of N cars on the right track, and rearrange these cars with the above transition stack, so that the odd cars are arranged in front of the even cars.

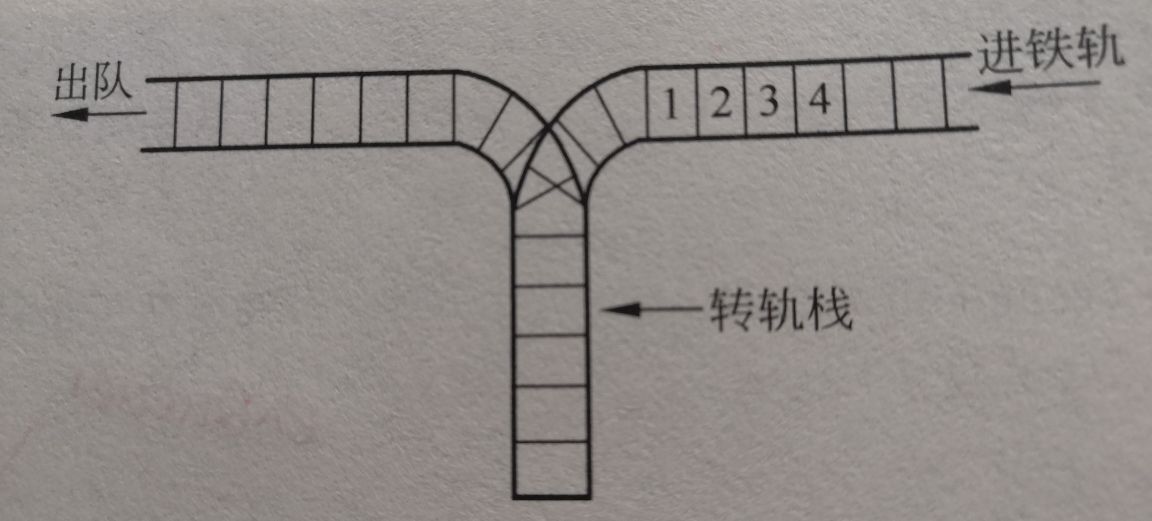
• Algorithm idea: regard the transition stack as a stack and the left track as a queue. Input the integer representing the number of the car on the right track one by one from the keyboard, and do the following processing according to its parity: if it is an odd number, insert it into the end of the queue representing the sequence queue of the left track; If it is an even number, it is inserted into the top of the sequential stack representing the transition stack. When all n integers are detected, all these integers have entered the queue or stack. At this time, first output the elements in the queue in the order of first in first out, and then output the elements in the queue in the order of last in first out.
  The algorithm directly uses two arrays st and qu to store the elements in the stack and queue respectively.

void fun()
{
	SqStack s;
	InitStack(s);
	SqQueue q;
	InitQueue(q);
	int n, x, i;
	ElemType num;
	printf("Input: n=");
	scanf("%d", &n);
	for (i = 1; i <= n; i++)
	{
		printf("The first%d Car number:", i);
		scanf("%d", &x);
		if (x % 2 == 0)
		{
			Push(s, x);
			printf("%d Enter the stack\n", x);
		}
		else
		{
			enQueue(q, x);
			printf("%d Join the team\n", x);
		}
	}
	printf("Train derailment operation:\n");
	while (!QueueEmpty(q))
	{
		deQueue(q, num);
		printf("%d Out of the team ", num);
	}
	while (!StackEmpty(s))
	{
		Pop(s, num);
		printf("%d Out of stack ", num);
	}
}

Program analysis

• Operation results:
  

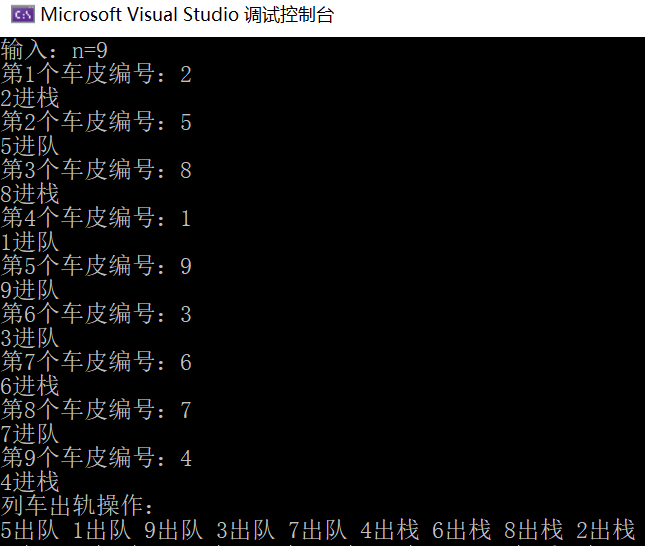
10. It is required to output all paths of the maze, and find the length of the first shortest path and the shortest path.

Algorithm idea: Link: Application of stack in maze problem

#include<stdio.h>
#define M 8 / / number of lines
#define N 8 / / number of columns
#define Maxsize 100 / / the maximum number of elements in the stack
int mg[M + 2][N + 2] = { //A maze surrounded by an outer frame of 1
	{1,1,1,1,1,1,1,1,1,1},{1,0,0,1,0,0,0,1,0,1},
	{1,0,0,1,0,0,0,1,0,1},{1,0,0,0,0,1,1,0,0,1},
	{1,0,1,1,1,0,0,0,0,1},{1,0,0,0,1,0,0,0,1},
	{1,0,1,0,0,0,1,0,0,1},{1,0,1,1,1,0,1,1,0,1},
	{1,1,0,0,0,0,0,0,0,1},{1,1,1,1,1,1,1,1,1,1} };
struct
{
	int i, j;
	int di;
}St[Maxsize], Path[Maxsize]; //Defines the stack and the array that holds the shortest path
int top = -1; //Stack top pointer	
int count = 1; //Path count
int minlen = Maxsize; //Shortest path length

void dispapath() //Output a path and find the shortest path
{
	int k;
	printf(" %5d: ", count++); //Output the count path
	for (k = 0; k <= top; k++)
		printf("(%d,%d)", St[k].i, St[k].j);
	printf("\n");
	if (top + 1 < minlen) //Compare and find the shortest path
	{
		for (k = 0; k <= top; k++) //Store the shortest path in path
			Path[k] = St[k];
		minlen = top + 1; //Store the shortest path length in minlen
	}
}

void dispminpath() //Output the first shortest path
{
	printf("The shortest path is as follows:\n");
	printf("Length:%d\n", minlen);
	printf("route:");
	for (int k = 0; k < minlen; k++)
		printf("(%d,%d)", Path[k].i, Path[k].j);
	printf("\n");
}

void mgpath(int xi, int yi, int xe, int ye)//Find maze path
{
	int i, j, i1, j1, di;
	bool find;
	top++; //Enter the stack
	St[top].i = xi;
	St[top].j = yi;
	St[top].di = -1;
	mg[xi][yi] = -1; //Initial block stacking
	while (top > -1) //Loop when stack is not empty
	{
		i = St[top].i; //Top block (i,j)
		j = St[top].j;
		di = St[top].di;
		if (i == xe && j == ye) //Found the exit
		{
			dispapath(); //Output a path
			mg[i][j] = 0; //Turn the exit into another path
			top--; //Exit back stack, that is, back a box
			i = St[top].i;
			j = St[top].j;
			di = St[top].di; //Make the stack top square current
		}
		find = false;	//Find the next walkable box (i1,j1)
		while (di < 4 && !find)
		{
			di++;
			switch (di)
			{
			case 0: i1 = i - 1; j1 = j; break;
			case 1: i1 = i; j1 = j + 1; break;
			case 2: i1 = i + 1; j1 = j; break;
			case 3: i1 = i; j1 = j - 1; break;
			}
			if (mg[i1][j1] == 0) find = true;
		}
		if (find)//Find the next walkable block (i1,j1) / / modify the di value of the original set-top element
		{
			St[top].di = di;
			top++;
			St[top].i = i1;
			St[top].j = j1;
			St[top].di = -1; //The next walkable block (11,j1) enters the stack
			mg[i1][j1] = -1; //Avoid going to the box repeatedly
		}
		else //If there is no path to go, the (i,j) box is back on the stack
		{
			mg[i][j] = 0; //Change this position to another path can go box
			top--;
		}
	}
	dispminpath(); //Output shortest path
}
					
int main()
{
	printf("All paths of the maze are as follows:\n");
	mgpath(1, 1, M, N);
	return 0;
}

Program analysis

• Operation results: