1. Establish the chain storage structure of binary tree (bracket representation)

• Algorithm idea:
  ① If ch = '(': it means that the node p just created has child nodes, and it needs to be stacked as the top node of the stack in order to establish the relationship between it and its child nodes (if a node has just been created, and the subsequent character is not '(', it means that the node is a leaf child node and does not need to be stacked). Then start processing the left child of the node and set K = 1 (indicating that the node created later will be the left child node of the top node of the stack). ② If ch = ')': it means that the child with the top node as the root node has been created, and it will be returned to the stack.
  ③ If ch = ',': it means to start processing the right child node of the stack top node, and set K = 2 (it means that the node created later will be the right child node of the current stack top node).
  ④ Other situations: it can only be a single character, corresponding to a node value in the binary tree. You need to create a node p to store the node value. According to the K value, the relationship between it and the top node of the stack is established. When k=1, take node P as the left child of the top node of the stack; When k=2, node P is the right child of the top node of the stack.

void CreateBTree(BiTNode* &b,ElemType *str)
{
	BiTNode* St[MaxSize], * p; //St array as sequential stack
	int top = -1, j = 0, k; //Top is the stack top pointer
	ElemType ch;
	b = NULL; //Initially, the binary chain is empty
	ch = str[j];
	while (ch != '\0') //Cycle through every character in str
	{
		switch (ch)
		{
		case '(':top++; St[top] = p; k = 1; break; //Start processing left child node
		case ')':top--; break; //The subtree of the top node of the stack has been processed
		case ',':k = 2; break; //Start processing right child node
		default:p = (BiTNode*)malloc(sizeof(BiTNode)); //Create a node with p pointing to it
			p->data = ch; //Store node value
			p->lchild = p->rchild = NULL; //Both the left and right pointers are set to null
			if (b == NULL) b = p; //If the root node has not been established, the node referred to by p is regarded as the root node
			else //Binary tree root node established
			{
				switch(k)
				{
					case 1:St[top]->lchild = p; break; //Create a new node as the left child of the top node of the stack
					case 2:St[top]->rchild = p; break; //Create a new node as the right child of the top node of the stack
				}
			}
		}
		j++; //Continue scanning str
		ch = str[j];
	}
}

2. A binary tree is known to be stored in a sequential structure, and the value of the nearest common ancestor node of the two nodes numbered i and j respectively is calculated.

• Algorithm idea: 1) if I > J, the level of node I is greater than or equal to that of node j. The parent node of node I is node i/2. If i/2=j, node i/2 is the nearest common ancestor of the original nodes I and j, if i/2 ≠ J. Then let i=i/2, that is, take the parent node of the node as the starting point and continue to search by recursive method.
  1) If J > I, the level of node j is greater than or equal to that of node I. The parent node of node j is node j/2. If j/2=i, node j/2 is the nearest common ancestor node of original node i and j, if j/2 ≠ I. Then let = j/2, that is, take the parent node of the node as the starting point and continue to search by recursive method. Repeat the above process until their nearest common ancestor node is found.

int Layer(TreeNode t[], int i) //Find the level of node i
{
	return log2(i) + 1;
}

ElemType Com_Anc(TreeNode t[], int i, int j)
{
	if (t[i].value != '#' && t[j].value != '#'/ / node exists
	{
		while (i != j) //Two numbers do not cycle at the same time
		{
			if (i > j) i = i / 2; //Look up for i's ancestors
			else j = j / 2; //Look up for j's ancestors
		}
		return t[i].value;
	}
}

Operation results

3. Assuming that the binary tree adopts the binary chain storage structure, calculate the number of nodes in layer k of binary tree b.

• Algorithm idea: Lnodenum(BiTNode *b,int k), H represents the node level referred to by b, and n is used to calculate the number of nodes in layer K. In the initial call, b is the root node pointer, h is 1, and n is assigned 0.

• The following algorithm is obtained based on the idea of preorder traversal:

int n = 0; //Global variable, used to count the number of nodes at layer k
void Lnodenum(BiTNode* b, int h, int k)
{
	if (b == NULL) return; //Empty tree direct return
	else //Dealing with non empty trees
	{
		if (k == h) n++; //When the currently accessed node is in layer k, n increases by 1
		else if (h < k) //If the current node level is less than k, the left and right subtrees are processed recursively
		{
			Lnodenum(b->lchild, h + 1, k);
			Lnodenum(b->rchild, h + 1, k);
		}
	}
}

4. Assuming that the binary tree adopts the binary chain storage structure, find the level (or depth) of the node with node value x in binary tree b.

• Algorithm idea: Level(BiTNode *b,ElemType x,int h). Its return value is to find the level of the node with node value x in binary tree b. returning 0 means it is not found. If b is an empty tree, return 0; If the node value of the current root node is x, h is returned; Otherwise, search in the left subtree (level H needs to be increased by 1). If it is not found in the left subtree, search in the right subtree (level H needs to be increased by 1).

int Level(BiTNode* b, ElemType x, int h) //h set initial value 1
{
	int lev;
	if (b == NULL) return 0;
	else if (b->data == x) return 1;
	else
	{
		lev = Level(b->lchild, x, h + 1); //Find in the left subtree
		if (lev != 0) return lev; //Found in the left subtree, return 1
		else lev = Level(b->rchild, x, h + 1); //Not found in the left subtree, and then find it in the right subtree
	}
}

5. Suppose that the binary tree adopts the binary chain storage structure to output the inverse sequence of paths from the root node to each leaf node.

• Algorithm idea: using the characteristics of post order traversal non recursive algorithm, change the access node to judge whether the node is a leaf node. If so, output all node values in the stack.

void AllPath(BiTNode* b)
{
	BiTNode* p, * r;
	bool flag;
	SqStack* st; //Define a sequential stack pointer st
	InitStack(st); //Initialize stack st
	p = b;
	do {
		while (p != NULL) //Scan all lower left nodes of node p and stack
		{
			Push(st, p); //Node p stack
			p = p->lchild; //Move to left child
		}
		r = NULL; //r points to the node just accessed, which is empty at the beginning
		flag = true; //A flag of true indicates that the top node of the stack is being processed
		while (!EmptyStack(st) && flag)
		{
			GetTop(st, p); //Fetch the current stack top node p
			if (p->rchild == r) //If the right child of node p is empty or is the node just accessed
			{
				if (p->lchild == NULL && p->rchild == NULL)
				{
					for (int i = st->top; i > 0; i--)
						printf("%c -> ", st->data[i]->data);
					printf("%c\n", st->data[0]->data);
				}
				Pop(st, p);
				r = p; //r points to the node just visited
			}
			else
			{
				p = p->rchild; //Turn to its right subtree
				flag = false; //Indicates that it is not currently the top node of the processing stack
			}
		}
	} while (!EmptyStack(st)); //Stack not empty loop
	printf("\n");
	DestroyStack(st); //Destroy stack
}

Operation results

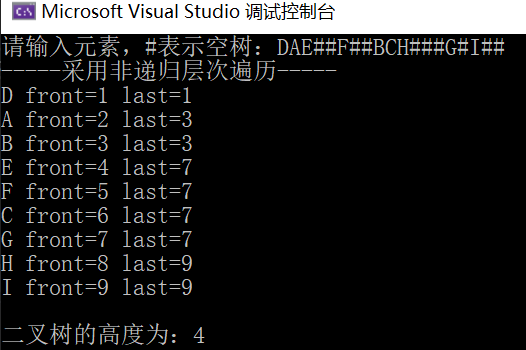
6. Convert the sequential storage structure of binary tree into binary chain storage structure.

• Algorithm idea: let the sequential storage structure of binary tree be a, and f(a,i) returns the binary chain storage structure with a[i] as the root node (the initial call is b=f(a,1)).

BiTNode* trans(SqTree t[], int i)
{
	BiTNode* b;
	if (i > MaxSize) return NULL;
	if (t[i].value == '#') return NULL;
	b = (BiTNode*)malloc(sizeof(BiTNode));
	b->data = t[i].value;
	b->lchild = trans(t, 2 * i);
	b->rchild = trans(t, 2 * i + 1);
	return b;
}

//PreOrder(trans(t, 1));

Operation results

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
value	D	A	B	E	F	C	G	#	#	#	#	H	#	#	I

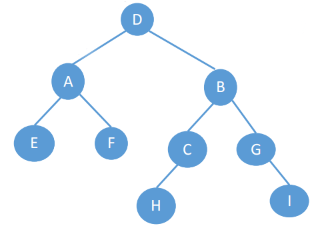
7. The bottom-up and right to left hierarchical traversal algorithm of binary tree is given.

• Algorithm idea: using the original hierarchical traversal algorithm, the pointer of each node is put on the stack while leaving the queue. After all nodes are put on the stack, they are accessed successively from the top of the stack, which is the required algorithm.

void LevelOrder(BiTNode* b)
{
	BiTNode* p;
	SqStack* st;
	InitStack(st);
	SqQueue* qu;
	InitQueue(qu);
	enQueue(qu, b);
	printf("Top down, left to right level traversal:");
	while (!EmptyQueue(qu))
	{
		deQueue(qu, p);
		Push(st, p);
		printf("%c ", p->data);
		if (p->lchild != NULL) enQueue(qu, p->lchild);
		if (p->rchild != NULL) enQueue(qu, p->rchild);
	}
	printf("\n Bottom up, right to left level traversal:");
	for (int i = st->top; i >= 0; i--)
	{
		Pop(st, p);
		printf("%c ", p->data);
	}
}

Operation results

8. Suppose the binary tree adopts the binary linked list storage structure to calculate the height of the binary tree.

• Method 1 (non recursive algorithm)

• Algorithm idea: using the post order traversal method, when dealing with the leaf node in the deepest layer (layer h), all nodes in layer h-1 are in the stack, and the depth of the current stack is the height of the binary tree.

int PostOrder(BiTNode* b)
{
	BiTNode* p, * r;
	bool flag;
	int count = 0, max = 0;
	SqStack* st; //Define a sequential stack pointer st
	InitStack(st); //Initialize stack st
	p = b;
	do {
		while (p != NULL) //Scan all lower left nodes of node p and stack
		{
			Push(st, p); //Node p stack
			count++; //Stack height + 1
			if (count > max) max = count;
			p = p->lchild; //Move to left child
		}
		r = NULL; //r points to the node just accessed, which is empty at the beginning
		flag = true; //A flag of true indicates that the top node of the stack is being processed
		while (!EmptyStack(st) && flag)
		{
			GetTop(st, p); //Fetch the current stack top node p
			if (p->rchild == r) //If the right child of node p is empty or is the node just accessed
			{
				printf("%c ", p->data); //Access node p
				Pop(st, p);
				count--; //Stack height - 1
				r = p; //r points to the node just visited
			}
			else
			{
				p = p->rchild; //Turn to its right subtree
				flag = false; //Indicates that it is not currently the top node of the processing stack
			}
		}
	} while (!EmptyStack(st)); //Stack not empty loop
	printf("\n");
	//DestroyStack(st); // Destroy stack
	return max;
}

Operation results

• The time complexity is O(n) and the space is O(max). Where n is the number of nodes in the binary tree and Max is the maximum depth of the stack.

• Method 2 (non recursive algorithm)

• Algorithm idea: use the idea of sequence traversal to record the number of layers. rear represents the sequence number of the last node in each layer, and front represents the sequence number of the current access node.

int LevelOrder(BiTNode* b)
{
	int front = 0, rear = 0, last = 1, level = 0; //last points to the rightmost node of the current layer
	if (b == NULL) return 0; //Null tree returns 0
	BiTNode* p;
	SqQueue* qu;
	InitQueue(qu);
	enQueue(qu, b); //Root node queue
	rear++;
	while (!EmptyQueue(qu)) //If the queue is not empty, cycle
	{
		
		deQueue(qu, p); //The queue element is out of the queue, that is, the node being accessed
		front++;
		printf("%c ", p->data);
		if (p->lchild != NULL) //The left child joined the team
		{
			enQueue(qu, p->lchild);
			rear++;
		}
		if (p->rchild != NULL) //Right child join the team
		{
			enQueue(qu, p->rchild);
			rear++;
		}
		if (front == last) //Process the rightmost node of this layer
		{
			level++; //Number of layers + 1
			last = rear; //last points to the lower layer
		}
	}
	return level;
}

Operation results

• Method 3 (recursive algorithm)

int Height(BiTNode* b)
{
	int left, right;
	if (b == NULL) return 0;
	left = Height(b->lchild);
	right = Height(b->rchild);
	return left > right ? left + 1 : right + 1;
}

Operation results

• Similar ideas are used to find the number of nodes in a layer, the number of nodes in each layer, the maximum width of the tree, etc.

① Number of nodes in a layer (non recursive)

int LevelOrder(BiTNode* b,int i) //Find the height of binary tree
{
	//front represents the sequence number of the first node of the current layer, and last represents the sequence number of the last node of the current layer
	//rear represents the sequence number of the last node in the next layer, and visit represents the sequence number of the current access node
	int front=1, rear = 0, last = 1, level = 0, visit = 0;
	if (b == NULL || i <= 0) return 0; //Returns 0 when the tree is empty or the parameter is incorrect
	if (b != NULL && i == 1) return 1;
	BiTNode* p;
	SqQueue* qu;
	InitQueue(qu);
	enQueue(qu, b); //Root node queue
	rear++;
	while (!EmptyQueue(qu)) //If the queue is not empty, cycle
	{
		deQueue(qu, p); //The queue element is out of the queue, that is, the node being accessed
		visit++; //visit indicates the sequence number of the node currently being accessed
		//printf("%c ", p->data);
		if (p->lchild != NULL)
		{
			enQueue(qu, p->lchild); //The left child joined the team
			rear++;
		}
		if (p->rchild != NULL)
		{
			enQueue(qu, p->rchild); //Right child join the team
			rear++;
		}
		if (visit == last) //If the currently accessed node is the rightmost node in the current layer
		{
			level++; //Number of layers + 1
			if (level == i)
			{
				printf("front=%d last=%d", front, last);
				return last - front + 1;
			}
			front = last + 1; //The sequence number of the first node of the next layer is the sequence number of the last node of the previous layer + 1
			last = rear; //Modify the sequence number of the last node of the next layer
		}
	}
}

① Number of nodes in a layer (recursive)

• The design algorithm is lnodenum (bitnode * B, int h, int k, int & n). H represents the node level referred to by B, and N is a reference parameter, which is used to calculate the number of nodes in layer K. In the initial call, B is the root node pointer, h is 1, and N is assigned to 0, that is, the call method is n=0; Lnodenum(b,1,k,n).

void Lnodenum(BiTNode* b, int h, int k, int& n)
{
	if (b == NULL) return; //Empty tree direct return
	else //Dealing with non empty trees
	{
		if (h == k) n++; //When the currently accessed node is in layer k, n increases by 1
		else if (h < k) //If the current node level is less than k, the left and right subtrees are processed recursively
		{
			Lnodenum(b->lchild, h + 1, k, n);
			Lnodenum(b->rchild, h + 1, k, n);
		}
	}
}

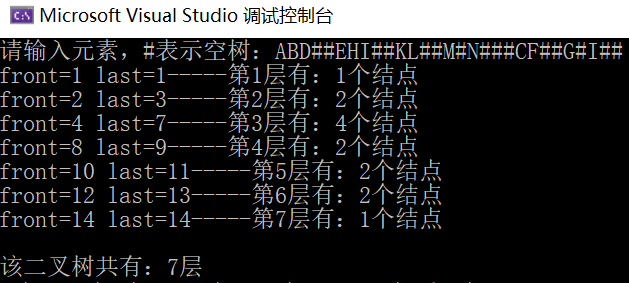
② Number of nodes per layer (non recursive)

int LevelOrder(BiTNode* b) //Find the height of binary tree
{
	//front represents the sequence number of the first node of the current layer, and last represents the sequence number of the last node of the current layer
	//rear represents the sequence number of the last node in the next layer, and visit represents the sequence number of the current access node
	int front, rear = 0, last = 1, level = 0, visit = 0;
	if (b == NULL) return 0; //Null tree returns 0
	BiTNode* p;
	SqQueue* qu;
	InitQueue(qu);
	enQueue(qu, b); //Root node queue
	rear++;
	while (!EmptyQueue(qu)) //If the queue is not empty, cycle
	{
		deQueue(qu, p); //The queue element is out of the queue, that is, the node being accessed
		visit++; //visit indicates the sequence number of the node currently being accessed
		//printf("%c ", p->data);
		if (p->lchild != NULL)
		{
			enQueue(qu, p->lchild); //The left child joined the team
			rear++;
		}
		if (p->rchild != NULL)
		{
			enQueue(qu, p->rchild); //Right child join the team
			rear++;
		}
		if (visit == last) //If the currently accessed node is the rightmost node in the current layer
		{
			level++; //Number of layers + 1
			if(level==1) front = last; //The first layer has only the root node
			printf("front=%d last=%d", front, last);
			printf("-----The first%d The layers are:%d Nodes\n", level, last-front + 1);
			front = last + 1; //The sequence number of the first node of the next layer is the sequence number of the last node of the previous layer + 1
			last = rear; //Modify the sequence number of the last node of the next layer
		}
	}
	return level;
}

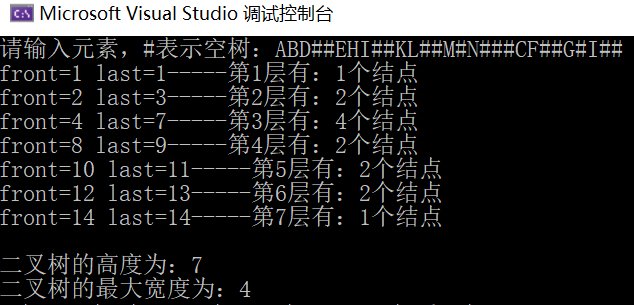
③ Maximum width of the tree (non recursive)

int LevelOrder(BiTNode* b) //Find the height of binary tree
{
	//front represents the sequence number of the first node of the current layer, and last represents the sequence number of the last node of the current layer
	//rear represents the sequence number of the last node in the next layer, and visit represents the sequence number of the current access node
	int front, rear = 0, last = 1, level = 0, visit = 0, maxwidth = 0;
	if (b == NULL) return 0; //Null tree returns 0
	BiTNode* p;
	SqQueue* qu;
	InitQueue(qu);
	enQueue(qu, b); //Root node queue
	rear++;
	while (!EmptyQueue(qu)) //If the queue is not empty, cycle
	{
		deQueue(qu, p); //The queue element is out of the queue, that is, the node being accessed
		visit++; //visit indicates the sequence number of the node currently being accessed
		//printf("%c ", p->data);
		if (p->lchild != NULL)
		{
			enQueue(qu, p->lchild); //The left child joined the team
			rear++;
		}
		if (p->rchild != NULL)
		{
			enQueue(qu, p->rchild); //Right child join the team
			rear++;
		}
		if (visit == last) //If the currently accessed node is the rightmost node in the current layer
		{
			level++; //Number of layers + 1
			if (level == 1) front = last; //The first layer has only the root node
			printf("front=%d last=%d", front, last);
			printf("-----The first%d The layers are:%d Nodes\n", level, last - front + 1);
			if (last - front + 1 > maxwidth) maxwidth = last - front + 1; //Compare the number of nodes in each layer
			front = last + 1; //The sequence number of the first node of the next layer is the sequence number of the last node of the previous layer + 1
			last = rear; //Modify the sequence number of the last node of the next layer
		}
	}
	printf("\n The height of binary tree is:%d", level);
	return maxwidth;
}