Computer experiment of data structure (Chapter II) IV

Computer experiment of data structure (Chapter II) III

12. In an incrementally ordered linear table, there are elements with the same value. If the storage method is a single linked list, remove the elements with the same value so that there are no duplicate elements in the table.

void DeleteEle(LinkList &L)
{
	LNode* p = L->next, *q;
	if (p == NULL) return;
	while (p->next != NULL)
	{
		q = p->next;
		if (p->data == q->data)
		{
			p->next = q->next;
			free(q);
		}
	else 
		p = p->next;
	}
}

Program analysis:

Operation results:
Time complexity: O(n); Space complexity: O(1)

13. Suppose there are two linear tables arranged in the order of increasing element values, which are stored in the form of single linked list. The two single linked lists are merged into a single linked list arranged in descending order of element values, and the nodes of the original two single linked lists are required to store the merged single linked list.

void ConList(LinkList& LA, LinkList& LB)
{
	LNode* pa = LA->next, * pb = LB->next, * p, * s = LA, * q;
	LA->next = NULL;
	while (pa != NULL && pb != NULL)
	{
		if (pa->data < pb->data)
		{
			p = pa;
			pa = pa->next;
			p->next = s;
			s->next = p;
			s = s->next;
		}
		else if (pa->data > pb->data)
		{
			p = pb;
			pb = pb->next;
			p->next = s;
			s->next = p;
			s = s->next;
		}
		else
		{
			p = pa;
			q = pb;
			pa = pa->next;
			pb = pb->next;
			p->next = s;
			s->next = p;
			s = s->next;
			q->next = s;
			s->next = q;
			s = s->next;
		}
	}
	if(pa==NULL) s->next = pb;
}

Program analysis:

Operation results:
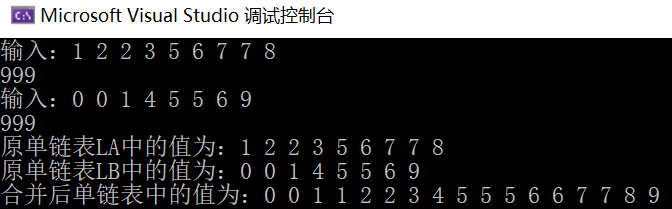
Time complexity: O(m+n), where m and N are the lengths of two single linked lists respectively; Space complexity: O(1)

14. Let A and B be two single linked lists (leading nodes), in which the elements are increasing in order. The single linked list C is generated from the common elements in A and B. It is required not to destroy the nodes of A and B.

Algorithm idea: Link: question 8 (2)

15. It is known that two linked lists A and B represent two sets respectively, and their elements are arranged incrementally. Compile the function, find the intersection of A and B, and store it in the A linked list.

Algorithm idea: Question 8 (2)
The difference between this question and 14 questions is that 14 questions require that the nodes of A and B are not destroyed, so the results should be put into the new linked list C, and this question can modify A linked list in A and B, so as not to open up A new space. The space complexity of question 14 is O(m+n), where m and N are the lengths of the two linked lists respectively; The spatial complexity of the problem is O(1).

16. Two Integer Sequences A = a 1 , a 2 , a 3 , ... , a n A=a_1,a_2,a_3,...,a_n A=a1, a2, a3,..., an and B = b 1 , b 2 , b 3 , ... , b n B=b_1,b_2,b_3,...,b_n B=b1, b2, b3,..., bn have been stored in two single linked lists to judge whether sequence B is A continuous subsequence of sequence A.

Algorithm idea: because two integer sequences have been stored in two linked lists, the operation starts from the first node of the two linked lists. If the corresponding data are equal, move the pointer back; If the corresponding data is not equal, the A-linked list starts from the successor of the last comparison node, and the b-linked list continues to compare from the first node until the end of the b-linked list indicates that the matching is successful. A linked list to the end and B linked list not to the end indicates failure.
In the operation, you should remember the starting node of A linked list each time, so that the next matching can start from its successor.

bool Pattern(LinkList& L1,LinkList &L2)
{
	LNode* p1 = L1->next, * p2 = L2->next, * pre = p1;
	while (p1 != NULL && p2 != NULL)
		{
			if (p1->data == p2->data)
			{
				p1 = p1->next;			
				p2 = p2->next;
			}
			else
			{
				pre = pre->next;
				p1 = pre;
				p2 = L2->next;
			}
		}
	if (p2 == NULL) return true;
	else return false;
}

Program analysis:

Operation results:

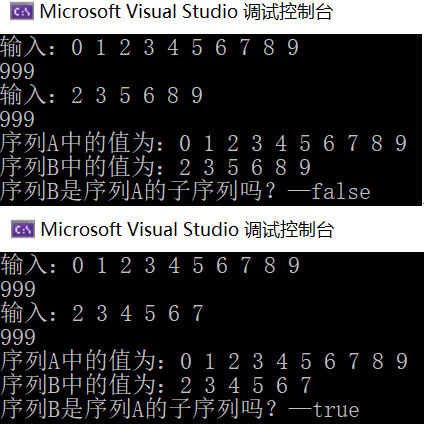
17. An algorithm is designed to judge whether the cyclic double linked list of the leading node is symmetrical.

Algorithm idea: Link: question 8

18. There are two circular single linked lists. The chain header pointers are h1 and h2 respectively. After linking the linked list h2 to the linked list h1, the linked list is required to remain in the form of circular linked list.

Algorithm idea: Link: Question 6 (case 3)

19. A circular single linked list with a leading node is set, and its node values are positive integers. Design an algorithm to repeatedly find the node with the lowest node value in the single linked list and output it, then delete the node from it until the single linked list is empty, and then delete the header node.

Algorithm idea: for the circular single linked list L, loop when it is not empty: find a minimum node (min points to the minimum node and premin points to its precursor node) once in each loop, delete it, and finally release the head node.

void DeleteMin(LinkList& L)
{
	LNode* p, * pre, * premin, * min;
	while (L->next != L)
	{
		p = L->next;
		pre = L; 
		premin = L;
		min = L->next;
		while (p != L)
		{	
			if (p->data < min->data)
			{
				min = p;
				premin = pre;
			}
			pre = p;
			p = p->next;
		}
		printf("min=%d\n", min->data);
		premin->next = min->next;
		free(min);
	}
	free(L);
}

Program analysis:

Operation results:

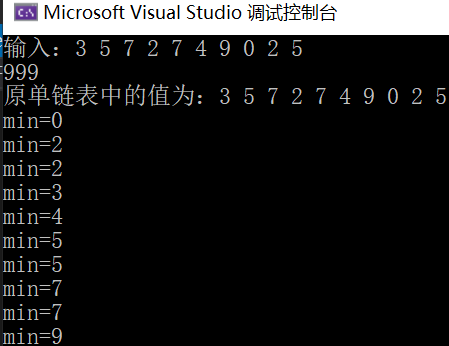
20. For an acyclic bidirectional linked list with a header node with a header pointer of L, each node has an access frequency domain freq in addition to the fields of PRED (predecessor pointer), data (data) and next (successor pointer). Before the linked list is enabled, its values are initialized to zero. Whenever a Locate(L,x) operation is performed in the linked list, the value of the freq field in the node whose element value is X is increased by 1, and the nodes in the linked list are arranged in the order of non increasing (decreasing) access frequency. At the same time, the most recently accessed nodes are arranged in front of the nodes with the same frequency, so that the frequently accessed nodes are always close to the header. Try to write the algorithm of Locate(L,x) operation that meets the above requirements. The operation is a function process and returns the address of the found node. The type is pointer type.

Algorithm idea: Question 4

21. A single table with header node is known, and the node structure is data and link. Suppose that the linked list only gives the header pointer list. Without changing the linked list, find the node at the penultimate position in the linked list (k is a positive integer). If the search is successful, the algorithm outputs the value of the data field of the node and returns 1; Otherwise, only 0 is returned.

Algorithm idea:
① count=0, p and q point to the first node at the same time.
② If p is empty, turn to ⑤.
③ If count equals k, then q points to the next node; Otherwise, count= count+1.
④ p points to the next node and turns to ②
⑤ If count is equal to k, the search succeeds, the value of the ata field of the node is output, and 1 is returned; Otherwise, it indicates that the k value exceeds the length of the linear table, the search fails and returns 0
⑥ Algorithm Jiedong.

bool Search(LinkList L, int k)
{
	LNode* p = L->link, * q = L->link;
	int count = 0;
	while (q != NULL)
	{
		if (count < k) count++; //Move pointer q to the last k bit of pointer p
		else p = p->link; //Pointer p and q move synchronously
		q = q->link;

	}
	if (count < k) return false; //The length of the linked list is less than k
	else
	{
		printf("Penultimate%d Location data Domain is:%d\n", k, p->data);
		return true;
	}
}

Program analysis:

Operation results:

22. It is assumed that the single linked list of the leading node is used to save words. When two words have the same suffix, they can share the same suffix storage space. Let str1 and str2 respectively point to the head node of the single linked list where the two words are located, and the linked list node structure is data and next. Please design an algorithm as efficient as possible in time to find out the starting position of the common lower level of the two linked lists pointed by str1 and str2 (such as the position P of the node where the character i is located in the figure).

Algorithm idea:
① Calculate the lengths m and n of the two linked lists referred to by Str1 and Str2 respectively.
② Align the two linked lists with the end of the list: make the pointers p and q point to the head node of Str1 and Str2 respectively. If m ≥ n, p goes first, so that p points to the m-n+1 node in the linked list; If m < n, make q point to the n-m+1 node in the linked list, even if the length from the node indicated by pointer p and q to the end of the table is equal.
③ Repeatedly move the finger p and q backward synchronously, and stop when p and q point to the same position, that is, the starting position of the common suffix, and the algorithm ends.

int ListLen(LinkList L)
{
	LNode* p = L->next;
	int len = 0;
	while (p != NULL)
	{
		len++;
		p = p->next;
	}
}

LNode* FindAddr(LinkList Str1, LinkList Str2)
{
	int m, n;
	LNode* p, * q;
	m = ListLen((Str1));
	n = ListLen((Str2));
	for (p = Str1; m > n; m--) p = p->next;
	for (q = Str2; m < n; n--) q = q->next;
	while (p != NULL && p->next != q->next)
	{
		p = p->next;
		q = q->next;
	}
	return p->next;
}

Program analysis:

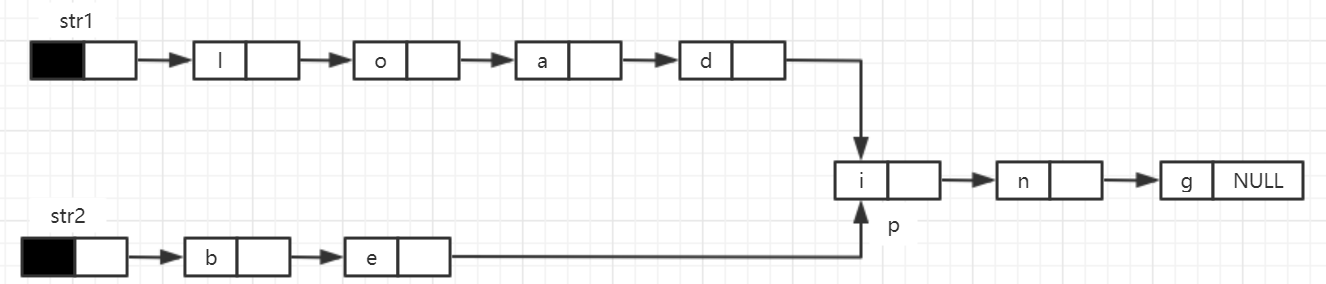
23. Save m integers in a single linked list. The node structure is [data][link], and | datal ≤ n(n is a positive integer). Now it is required to design an algorithm with time complexity as efficient as possible. For the nodes with equal absolute values of data in the linked list, only the first node is retained and the other nodes with equal absolute values are deleted.

Algorithm idea: space for time, use auxiliary array to record the values in the linked list.

void DeleEle(LinkList& L)
{
	int a[10] = { 0 }; //
	LNode* p = L->next, * pre = L;
	while (p != NULL)
	{
		a[abs(p->data)]++;
		if (a[abs(p->data)] > 1)
		{
			pre->next = p->next;
			free(p);
			p = pre->next;
		}
		else 
		{
			pre = pre->next;
			p = p->next;
		}
	}
}

Program analysis:

Operation results:
Time complexity: O(m); Space complexity O(n):

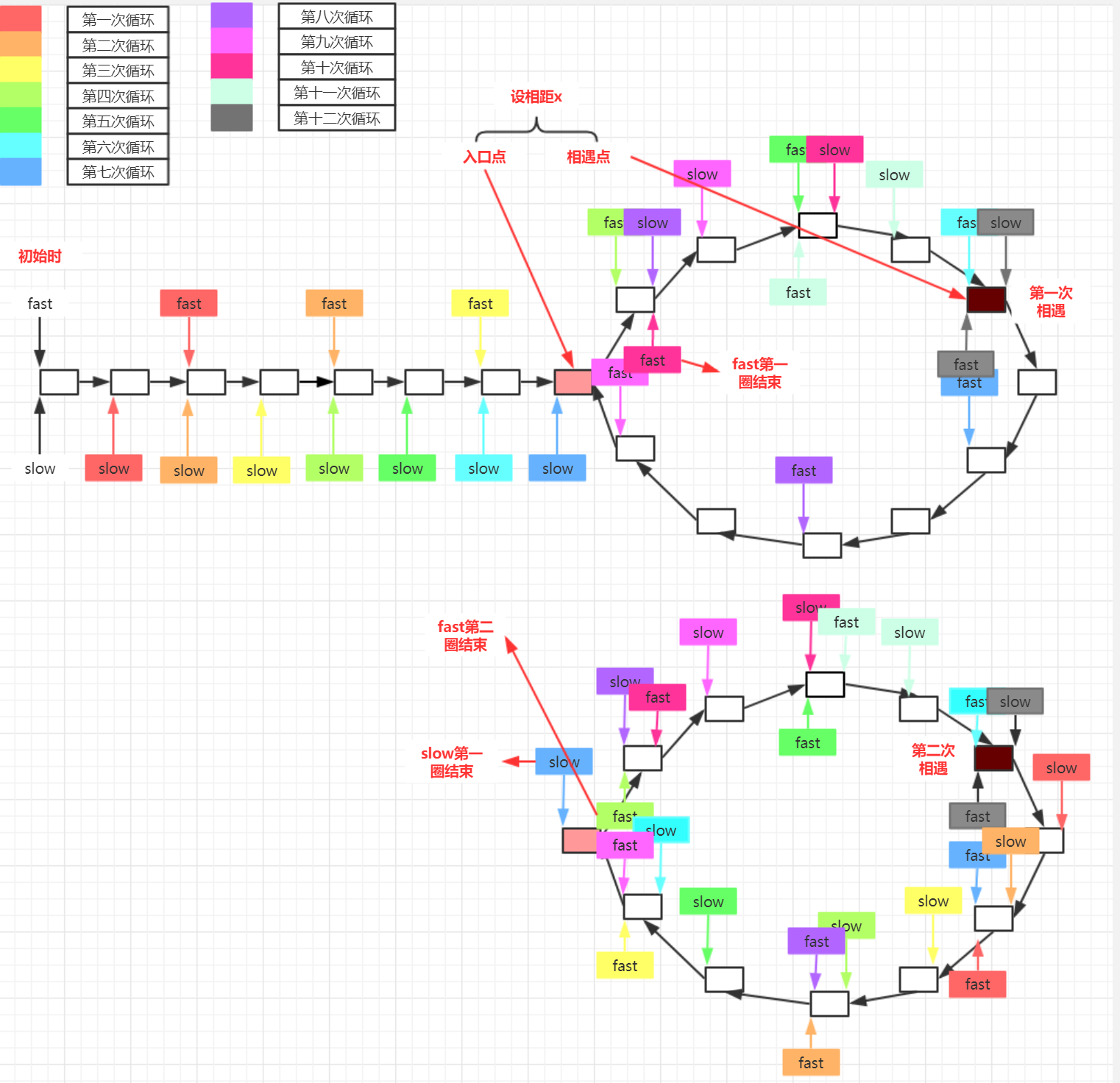
24. Judge whether a linked list has a ring. If so, find the entry point of the ring and return it. Otherwise, return NULL.

Algorithm idea: set the fast and slow pointers to fast and slow respectively, and point to the chain header head at the beginning. Slow takes one step at a time, that is, slow = slow - > next. Fast takes two steps at a time, that is, fast = Fast - > next - > next. Because fast moves faster than slow, if there is a ring, fast will enter the ring first, and slow will enter the ring later. When both pointers enter the ring, after several operations, the two pointers will meet on the ring. In this way, you can judge whether a linked list has a ring.

LNode* FindLoopStart(LNode* head)
{
	LNode* fast = head, * slow = head; //Set the speed of two pointers
	while (slow != NULL && fast->next != NULL)
	{
		slow = slow->next; //One step at a time
		fast = fast->next; //Take two steps at a time
		if (slow == fast) break; //meet
	}
	if (slow == NULL || fast->next == NULL) return NULL; //If there is no ring, NULL is returned
	LNode* p1 = head, * p2 = slow; //Point to the starting point and the meeting point respectively
	while (p1 != p2)
	{
		p1 = p1->next;
		p2 = p2->next;
	}
	return p1; //Return to entry point
}

Program analysis:

Four related questions:
① : judge whether the single linked list has a ring?
② : if there is a ring, what is the inlet of the ring?
③ : find ring length
④ : total length

Question 1: if the single linked list has a ring, set the speed two pointers. After several moving operations, it will meet at a certain time. Otherwise, it will eventually move to the end of the table (that is, NULL).
Problem 2: let the distance from the head node to the entry point of the ring be a, the distance from the entry point of the ring along the direction of the ring to the meeting point be x, and the ring length be r. fast bypasses n cycles when meeting. At this time, the distance traveled by slow d=(a+x); Distance traveled by fast 2d=(a+x+nr). Then there is 2(a+x)=a+nr+x. therefore, two pointers can be set, one pointing to head and the other pointing to the meeting point. The two pointers move synchronously (one step at a time). The meeting point is the entry point of the ring.
Question 3: save the meeting point, then move a pointer backward from the meeting point, record the number of nodes passed until the pointer returns to the meeting point, and then calculate the ring length.
Question 4: make a pointer move backward from the first node to the meeting point, and record the number of nodes passed. This length plus the ring length is the table length.

25. Set linearity table L = ( a 1 , a 2 , a 3 , ... , a n − 2 , a n − 1 , a n ) L=(a_1,a_2,a_3,...,a_{n-2},a_{n-1},a_n) L=(a1, a2, a3,..., an − 2, an − 1, an) use the single linked list of the leading nodes to save, rearrange the nodes in L to obtain the linear table L ′ = ( a 1 , a n , a 2 , a n − 1 , a 3 , a n − 2 , . . . ) L'=(a_1,a_n,a_2,a_{n-1},a_3,a_{n-2},...) L′=(a1,an,a2,an−1,a3,an−2,...).

Algorithm idea: ① first find the middle node of the linked list L and set two pointers p and q. pointer p takes one step each time and q takes two steps each time. When pointer q reaches the end of the chain, pointer p is just at the middle node of the linked list;
② Then, the nodes of the second half of L are reversed in situ;
③ Take a node from the front and back segments of the single linked list and rearrange it as required.

void ChangeList(LinkList& L)
{
	LNode* p = L, * q = L, * r, * s;
	while (q->next != NULL) //Addressing intermediate node
	{
		p = p->next; //p take one step
		q = q->next;
		if (q->next != NULL) q = q->next; //q take two steps
	}
	q = p->next; //The node referred to by p is the intermediate node, and q is the first node of the second half of the linked list
	p->next = NULL;
	while (q != NULL) //Reverse the second half of the linked list
	{
		r = q->next;
		q->next = p->next;
		p->next = q;
		q = r;
	}
	s = L->next; //s points to the first data node of the first half, that is, the insertion point
	q = p->next; //q points to the first data node in the second half
	p->next = NULL;
	while (q != NULL) //Insert the node of the second half of the linked list into the specified position
	{
		r = q->next; //r points to the next node in the second half
		q->next = s->next; //Insert the q pointed node after the pointed node
		s->next = q;
		s = q->next; //s points to the next insertion point of the first half
		q = r;	
	}
}

Program analysis:

Operation results:
Time complexity: O(n); Space complexity: O(1)

26. An integer array A[1... N] with a length of N. given the integer X, please design one with a time complexity of no more than O ( n l o g 2 n ) O(nlog_2^n) O(nlog2n) algorithm to find all integer pairs in this array whose sum of two is equal to X (each element is output only once).

Algorithm idea: if you think of sorting, the problem will be solved. First, a time complexity is O ( n l o g 2 n ) O(nlog_2^n) The sorting algorithm of O(nlog2n) sorts A[1... N] from small to large. You can use quick sorting (or two-way merging, etc.), and then start from the small end (i=1) and the large end (j=N) of the array: if A[i]+A[j] ≤ X, I + +; If A[i]+A[j] > X, j –; Otherwise, output A[i], A[j], and then I + +, j –; Until I > j stops.)

Keywords: C Algorithm data structure linked list Visual Studio

Added by Beatnik on Sat, 01 Jan 2022 00:54:08 +0200

Programming VIP

Computer experiment of data structure (Chapter II) IV

12. In an incrementally ordered linear table, there are elements with the same value. If the storage method is a single linked list, remove the elements with the same value so that there are no duplicate elements in the table.

Program analysis:

Program analysis:

14. Let A and B be two single linked lists (leading nodes), in which the elements are increasing in order. The single linked list C is generated from the common elements in A and B. It is required not to destroy the nodes of A and B.

15. It is known that two linked lists A and B represent two sets respectively, and their elements are arranged incrementally. Compile the function, find the intersection of A and B, and store it in the A linked list.

16. Two Integer Sequences A = a 1 , a 2 , a 3 , ... , a n A=a_1,a_2,a_3,...,a_n A=a1, a2, a3,..., an and B = b 1 , b 2 , b 3 , ... , b n B=b_1,b_2,b_3,...,b_n B=b1, b2, b3,..., bn have been stored in two single linked lists to judge whether sequence B is A continuous subsequence of sequence A.

Program analysis:

17. An algorithm is designed to judge whether the cyclic double linked list of the leading node is symmetrical.

18. There are two circular single linked lists. The chain header pointers are h1 and h2 respectively. After linking the linked list h2 to the linked list h1, the linked list is required to remain in the form of circular linked list.

Program analysis:

Program analysis:

Program analysis:

Program analysis:

24. Judge whether a linked list has a ring. If so, find the entry point of the ring and return it. Otherwise, return NULL.

Program analysis:

Program analysis:

26. An integer array A[1... N] with a length of N. given the integer X, please design one with a time complexity of no more than O ( n l o g 2 n ) O(nlog_2^n) O(nlog2n) algorithm to find all integer pairs in this array whose sum of two is equal to X (each element is output only once).

Popular Keywords