bulge is a very important concept in AutoCAD. bulge controls the size and direction of radian between two points. Various complex images may be composed of hundreds of arcs. The data exported from AutoCAD also has this value, which is generally in the form of two point coordinates and one convexity value. Therefore, understanding the concept of convexity is an important prerequisite for dealing with AutoCAD files. This paper will briefly introduce the concept of convexity and show how to scribe according to point coordinates and convexity.

Convexity demonstration program

1 concept of convexity

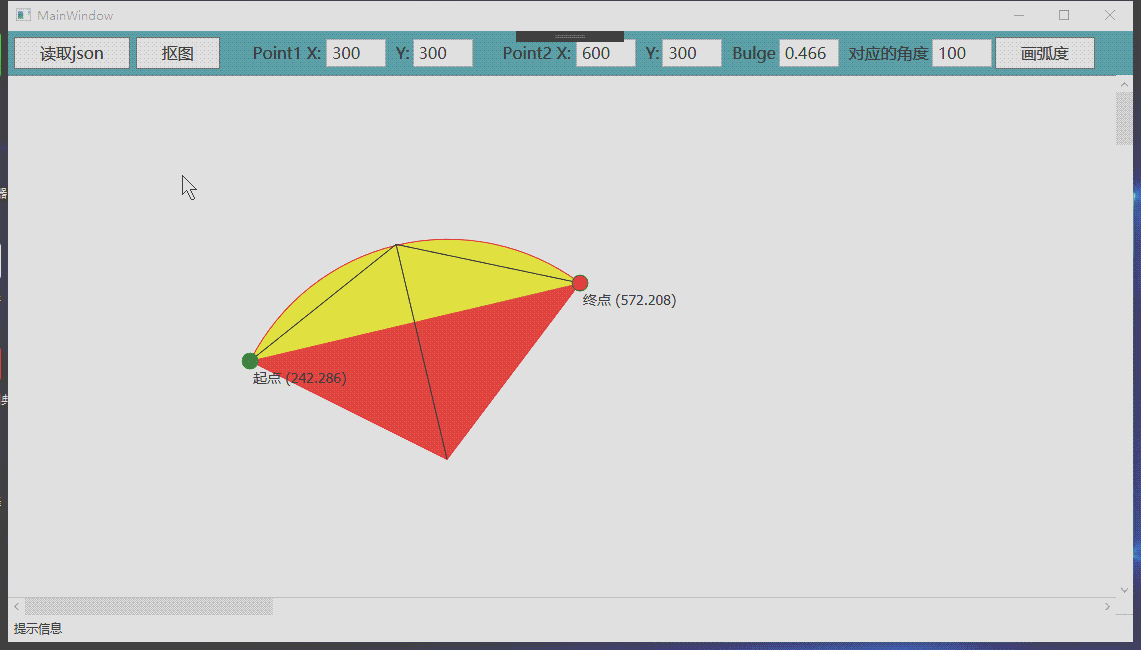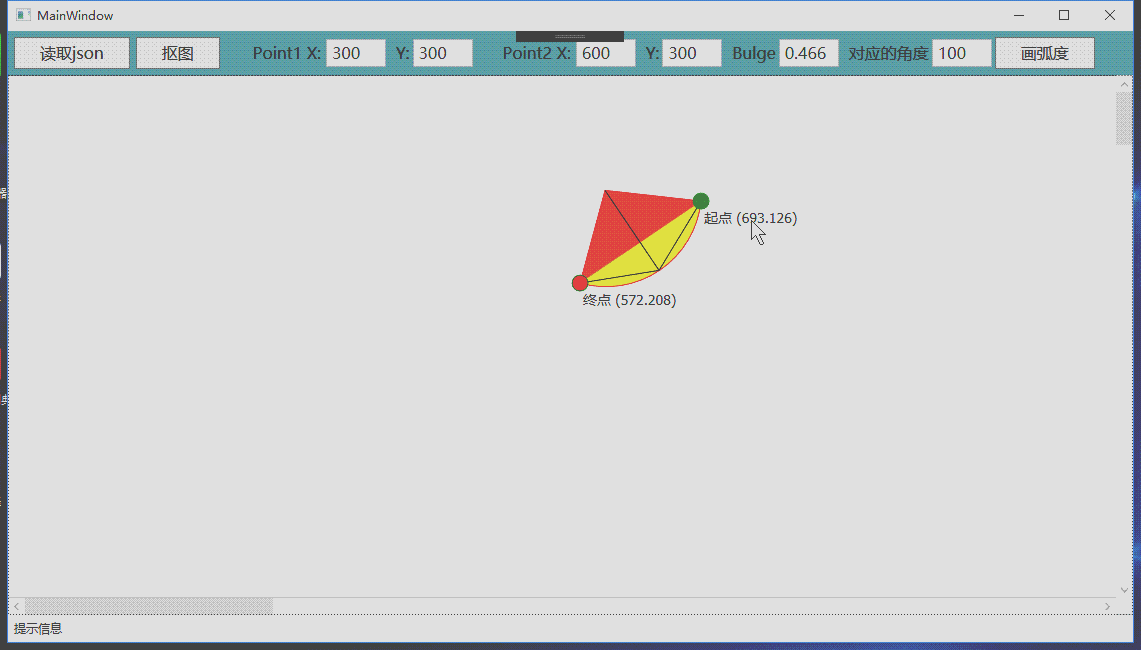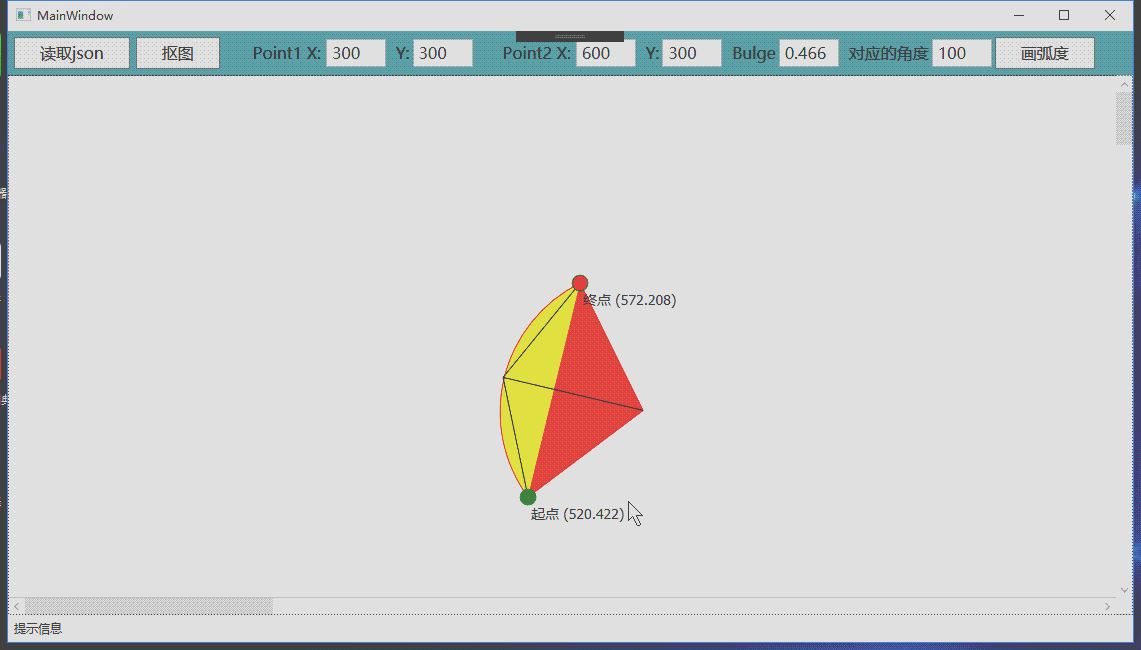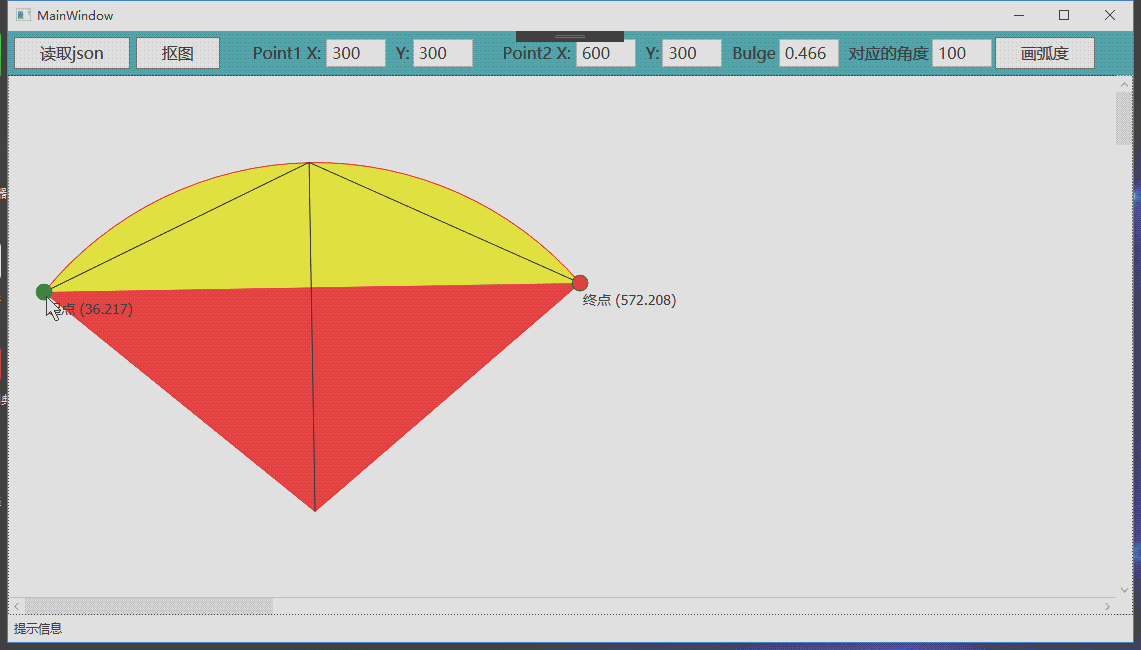
Convexity has two functions, controlling the size and direction of the vertex radian. If you draw an arc through two coordinate points, there will be countless possibilities, so you must introduce a third parameter to determine the only arc passing through these two points. This parameter is convexity.

Convexity reflects the corresponding radian between two points. Its specific value is the tangent of 1 / 4 of the angle contained in this arc. The maximum radian corresponding to two points is infinite, close to 360 degrees, and the corresponding value of convexity is the tangent value close to 90 degrees, so the maximum convexity is infinite.

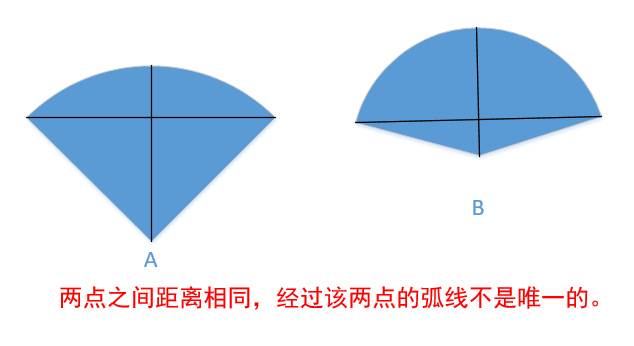
Carefully observe the above figure. The radian of figure B is greater than that of figure A, but the radius of figure B is smaller than that of figure A.

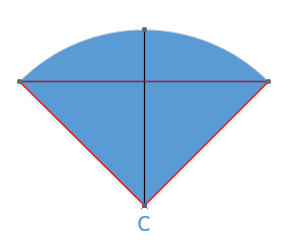
Why can the arc be uniquely determined by introducing the convexity value? When the convexity is determined, the radius corresponding to the radian is determined. Look at figure C below. The part marked by the red line is an isosceles triangle. When the length of the bottom edge and the angle of the vertex of the isosceles triangle are determined, the size of a triangle can be uniquely determined (belonging to the geometry knowledge of junior middle school). The two waist lengths of an isosceles triangle are the radius of a circle.

2. Calculate and draw according to convexity

Different drawing functions require different parameters. I'll explain how to draw according to the specific drawing function.

The WPF drawing context class is DrawingContext, which has a drawing function

public abstract void DrawGeometry(Brush brush, Pen pen, Geometry geometry);

This function is very simple, but it can draw any graph; Because the Geometry class is so powerful, it can describe any Geometry. Take a look at the following code:

 void AddArc(PathGeometry pathGeometry, System.Windows.Point point1, System.Windows.Point point2,  double bulge, double radius)
        {
            PathFigure pathFigure = new PathFigure();
            pathFigure.StartPoint = point1;//starting point

            ArcSegment arcSegment = new ArcSegment();
            arcSegment.Point = point2; //End
      
            //radius
            arcSegment.Size = new System.Windows.Size(radius, radius);

            //Corresponding angle
            double radian = Math.Atan(bulge) * 4;
            double angle = radian * 180 / Math.PI;
            arcSegment.RotationAngle =Math.Abs(angle); 
            //Is the direction of the radian clockwise or counterclockwise
            arcSegment.SweepDirection = bulge>0? SweepDirection.Clockwise:SweepDirection.Counterclockwise;
            //Is it greater than 180 degrees
            arcSegment.IsLargeArc = Math.Abs(bulge) > 1;
            pathFigure.Segments.Add(arcSegment);

            pathGeometry.Figures.Add(pathFigure);
        }

The above code realizes drawing according to two points, convexity and circle radius. (the radius is calculated according to the first three, and the algorithm will be described later)

One PathGeometry It consists of one or more graphics and PathFigure. A PathFigure is a series of closed or unclosed line segments or arcs. ArcSegment represents an arc, add it to the PathFigure, and then add the PathFigure to the Geometry, so that the arc can be drawn according to the DrawGeometry. Functions are annotated and very easy to understand.

Another parameter of ArcSegment is the radius of the circle. In fact, the radius can be derived from two points and 'convexity. I don't know why ArcSegment doesn't calculate it for us. Let's talk about how to calculate the radius.

3 calculate the radius according to the convexity

  public static double CalBulgeRadius(System.Windows.Point point1, System.Windows.Point point2, double bulge)
        {
            //Calculate vertex angle
            double cicleAngle = Math.Atan(bulge) * 4;

            //Distance between two points
            double pointLen = ImageHelper.CalPointLen(point1, point2);
            //Extrapolation according to positive value
            double radius = (pointLen / 2) / Math.Sin(cicleAngle / 2);
            return Math.Abs(radius);
        }

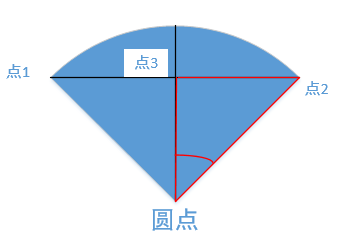Looking at the left figure, we can see that the positive value of half of the angle corresponding to the vertex is the length between two points divided by the radius. From this point, the radius can be calculated.

3 Calculation dot

Although the above function can draw an arc, we still don't know the coordinates of the center of the circle. Here's how to derive the center coordinates.

 

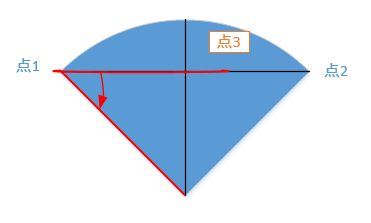
A concept here is rotation, which divides solving the center coordinates into two steps. The first step is to take a point (point 3) between two points, and the length from this point to point 1 is the radius; The second step is to rotate this point by a certain angle to obtain the center coordinates.

Find point 3:

          //Distance between two points
            double pointLen = ImageHelper.CalPointLen(point1, point2);

            //Ratio of radius to distance between two points
            double lenRate = radius / pointLen;
            System.Windows.Point midPoint = ImageHelper.GetMidPoint(point1, point2, lenRate);


  internal static System.Windows.Point GetMidPoint(System.Windows.Point pt1, System.Windows.Point pt2, double lenRate)
        {
            Debug.Assert(lenRate>=0);
            if (lenRate == 1)
                return pt2;
            if (lenRate == 0)
                return pt1;

            System.Windows.Point result = new System.Windows.Point();
            result.X = pt1.X + lenRate * (pt2.X - pt1.X);
            result.Y = pt1.Y + lenRate * (pt2.Y - pt1.Y);
            return result;
        }

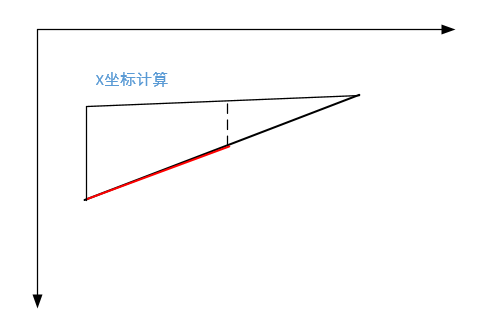
According to the geometric knowledge, we can know that the ratio between the radius and two points is the same as the ratio between the X coordinate of point 3 and the X coordinate of two points, so we can calculate the X coordinate. Similarly, you can find the Y coordinate.

Rotation:

Point 3 is centered on point 1, rotates a certain angle, and point 3 falls on the center of the circle. The rotation angle is not difficult to calculate, the vertex angle is known, and it is an isosceles triangle, so the base angle of the triangle is easy to calculate.

Rotation calculation involves two-dimensional vector operation, however NET provides us with class Matrix.

 public static System.Drawing.Point RotationAt(System.Drawing.Point pointMove, System.Drawing.Point removeAt, 
            double rotateAngle, bool clockwise)
        {
            if (rotateAngle == 0)
                return pointMove;

            lock (matrix)
            {
                matrix.Reset();
                //Sets the angle of rotation
                matrix.Rotate((float)(clockwise ? rotateAngle : -rotateAngle));

                //Rotate relative to removeAt
                System.Drawing.Point pt2 = new System.Drawing.Point(pointMove.X - removeAt.X, pointMove.Y - removeAt.Y);
                System.Drawing.Point[] pts = new System.Drawing.Point[] { new System.Drawing.Point(pt2.X, pt2.Y) };
                matrix.TransformPoints(pts);

                //Then change to the dot position
                System.Drawing.Point result = new System.Drawing.Point(pts[0].X + removeAt.X, pts[0].Y + removeAt.Y);
                return result;
            }
        }

Postscript: drawing on two-dimensional coordinates requires a certain geometric foundation and spatial imagination. Initial contact with this kind of programming is still difficult. We need to add some geometry knowledge and think more at the same time. One day, we will feel suddenly enlightened.