According to the middle order traversal and post order traversal of a tree, a binary tree is constructed.
Note: you can assume that there are no duplicate elements in the tree.
For example, give
inorder traversal= [9,3,15,20,7] postorder traversal postorder = [9,15,7,20,3] returns the following binary tree:

1, Train of thought
First, recall how to construct a unique binary tree according to two orders. I believe everyone should be clear about the theoretical knowledge, that is, the last element of the later ordered array is the cutting point, cut the middle ordered array first, and cut the back ordered array according to the middle ordered array. Cut down layer by layer. The last element of each subsequent array is the node element. If we look at two sequences with the naked eye and draw a binary tree, it should be drawn every minute.
The flow chart is as follows:
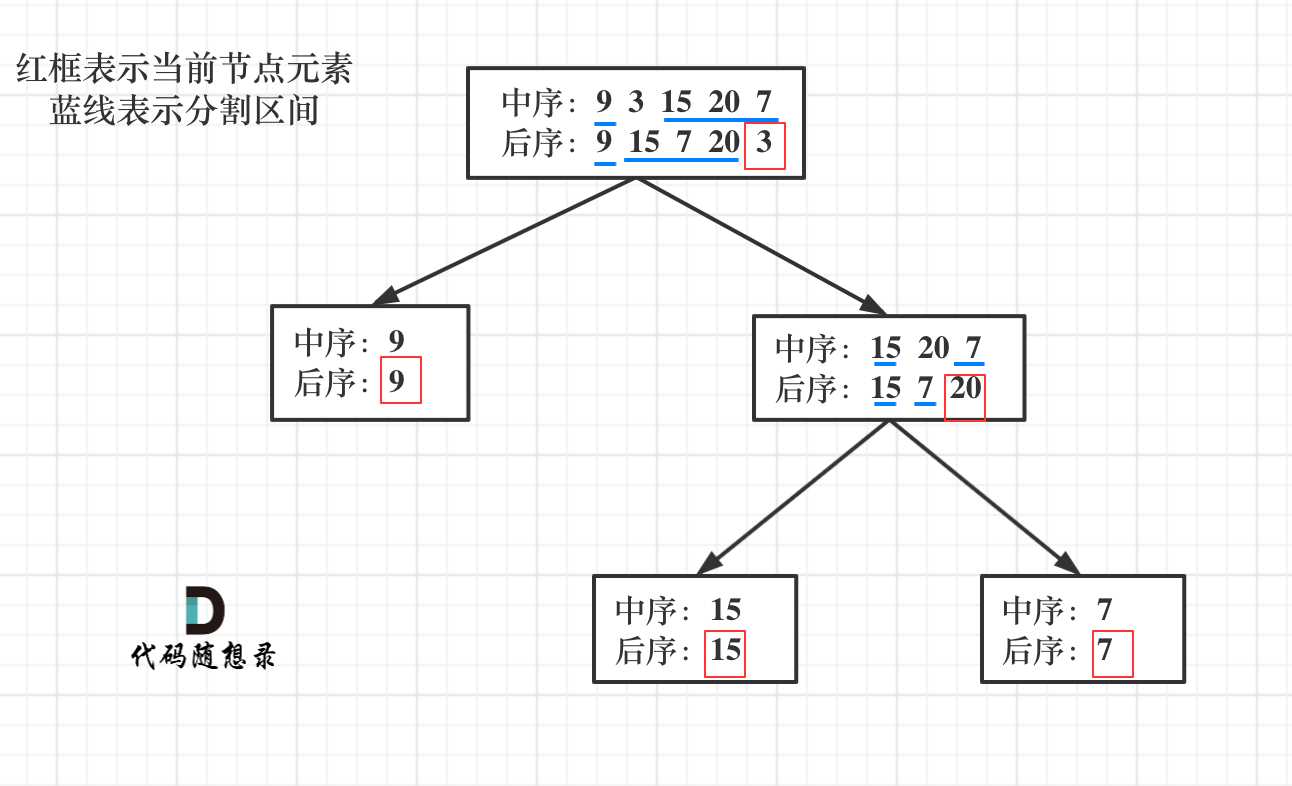
So how should the code be written? When it comes to cutting layer by layer, you should think of recursion. Let's take a look at the following steps:
-
Step 1: if the array size is zero, it indicates that it is an empty node.
-
Step 2: if it is not empty, take the last element of the subsequent array as the node element.
-
Step 3: find the position of the last element in the ordered array as the cutting point
-
Step 4: cut the middle order array into middle order left array and middle order right array (don't reverse the order, you must cut the middle order array first)
-
Step 5: cut the post order array into the post order left array and post order right array
-
Step 6: recursively handle the left and right intervals
It is not difficult to write the following code: (write the framework first)
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
// First step
if (postorder.size() == 0) return NULL;
// Step 2: the last element of the array is the current intermediate node
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
// Leaf node
if (postorder.size() == 1) return root;
// Step 3: find the cutting point
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Step 4: cut the middle order array to get the middle order left array and middle order right array
// Step 5: cut the post order array to get the post order left array and post order right array
// Step 6
root->left = traversal(Middle order left array, Postorder left array);
root->right = traversal(Middle right array, Postorder right array);
return root;
}
The difficulty you should find is how to cut, and it is easy to get confused if the boundary value is not found well. At this time, we should pay attention to determine the cutting standard, whether it is left closed, right open, left open and closed, or left closed and closed. This is the invariant, which should be maintained in recursion.
In the process of cutting, there will be four intervals. If you don't grasp the variables, you will close left and open right for a while, and close left and close again for a while. It will be messy! I am here Array: every time we encounter dichotomy, it will be discarded as soon as we see it and write it
(opens new window) and Array: this loop can turn many people!
(opens new window) The importance of loop invariants has been emphasized in. It is very important to adhere to loop invariants in binary search and the solution of spiral matrix. First, we should cut the middle order array. Why do we cut the middle order array first? The cutting point is the last element of the subsequent array, which is used to cut the middle order array, so it is necessary to cut the middle order array first.
The middle order array is relatively easy to cut. Find the position of the cutting point (the last element of the later order array) in the middle order array, and then cut. In the following code, I adhere to the principle of closing left and opening right:
// Find the cutting point of the middle order traversal
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Left closed right open interval: [0, delimiterIndex)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
// [delimiterIndex + 1, end)
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );Next, we will cut the sequential array. First, the last element of the sequential array cannot be specified. This is the cutting point and the element of the middle node of the current binary tree, which has been used. How to find the cutting point of the sequential array? The sequential array does not have a clear cutting element to cut left and right. Unlike the sequential array, which has a clear cutting point, the cutting points can be separated from left and right At this time, a very important point is that the size of the middle order array must be the same as that of the post order array (this is inevitable). We have cut the middle order array into the left middle order array and the right middle order array, so the post order array can be cut according to the size of the left middle order array, and cut into the left rear order array and the right rear order array.
The code is as follows:
// The postmaster discards the end element because this element is the intermediate node and has been used postorder.resize(postorder.size() - 1); // Close left and open right. Note that the left middle order array size is used as the cutting point: [0, leftInorder.size) vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size()); // [leftInorder.size(), end) vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
At this time, the middle order array is cut into the left middle order array and the right middle order array, and the rear order array is cut into the left rear order array and the right rear order array.
Next, you can recurse. The code is as follows:
root->left = traversal(leftInorder, leftPostorder); root->right = traversal(rightInorder, rightPostorder);
2, C + + complete code
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
if (postorder.size() == 0) return NULL;
// The last element of the array is the current intermediate node
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
// Leaf node
if (postorder.size() == 1) return root;
// Find the cutting point of the middle order traversal
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Cut ordered array
// Left closed right open interval: [0, delimiterIndex)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
// [delimiterIndex + 1, end)
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
// postorder discards the end element
postorder.resize(postorder.size() - 1);
// Cut sequential array
// It is still closed on the left and open on the right. Note that the size of the left middle order array is used as the cutting point
// [0, leftInorder.size)
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
// [leftInorder.size(), end)
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, postorder);
}
};
I believe that even if you have clear ideas, the code must be a variety of problems, so you must add logs to debug to see if you cut according to your own ideas. Don't simulate your brain. The more you think about it, the more confused you become.
The code with log is as follows: (the code with log should not be submitted on leetcode, which is easy to timeout)
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
if (postorder.size() == 0) return NULL;
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
if (postorder.size() == 1) return root;
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
postorder.resize(postorder.size() - 1);
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
// Click for log
cout << "----------" << endl;
cout << "leftInorder :";
for (int i : leftInorder) {
cout << i << " ";
}
cout << endl;
cout << "rightInorder :";
for (int i : rightInorder) {
cout << i << " ";
}
cout << endl;
cout << "leftPostorder :";
for (int i : leftPostorder) {
cout << i << " ";
}
cout << endl;
cout << "rightPostorder :";
for (int i : rightPostorder) {
cout << i << " ";
}
cout << endl;
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, postorder);
}
};
At this time, it should be found that the performance of the above code is not good. A new vector (i.e. array) should be defined for each layer of recursion, which is time-consuming and space-consuming, but the above code is best understood. In order to facilitate readers' understanding, we use the above code to explain it.
The following is the code version written with the following table index: (the idea is the same, but there is no need to define the vector repeatedly, and the following table index is used to split each time)
3, C + + optimized version
class Solution {
private:
// Middle order interval: [inorderBegin, inorderEnd), post order interval [postorderbegin, postordendend)
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
if (postorderBegin == postorderEnd) return NULL;
int rootValue = postorder[postorderEnd - 1];
TreeNode* root = new TreeNode(rootValue);
if (postorderEnd - postorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Cut ordered array
// Left middle order interval, left closed, right open [leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// Right middle order interval, left closed right open [rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// Cut sequential array
// Left post order interval, left closed right open [leftPostorderBegin, leftPostorderEnd)
int leftPostorderBegin = postorderBegin;
int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // The end position is the size of the middle order interval to be added
// Right post order interval, left closed right open [rightPostorderBegin, rightPostorderEnd)
int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
int rightPostorderEnd = postorderEnd - 1; // Exclude the last element, which is already a node
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
// Principle of left closing and right opening
return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
}
};
Then, if this version is written, you still need to log for debugging. The logged version is as follows: (this version should not be submitted on leetcode, which is easy to timeout)
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
if (postorderBegin == postorderEnd) return NULL;
int rootValue = postorder[postorderEnd - 1];
TreeNode* root = new TreeNode(rootValue);
if (postorderEnd - postorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Cut ordered array
// Left middle order interval, left closed, right open [leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// Right middle order interval, left closed right open [rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// Cut sequential array
// Left post order interval, left closed right open [leftPostorderBegin, leftPostorderEnd)
int leftPostorderBegin = postorderBegin;
int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // The end position is the size of the middle order interval to be added
// Right post order interval, left closed right open [rightPostorderBegin, rightPostorderEnd)
int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
int rightPostorderEnd = postorderEnd - 1; // Exclude the last element, which is already a node
cout << "----------" << endl;
cout << "leftInorder :";
for (int i = leftInorderBegin; i < leftInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "rightInorder :";
for (int i = rightInorderBegin; i < rightInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "leftpostorder :";
for (int i = leftPostorderBegin; i < leftPostorderEnd; i++) {
cout << postorder[i] << " ";
}
cout << endl;
cout << "rightpostorder :";
for (int i = rightPostorderBegin; i < rightPostorderEnd; i++) {
cout << postorder[i] << " ";
}
cout << endl;
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
}
};
4, Constructing binary tree from preorder and inorder traversal sequences
According to the preorder traversal and inorder traversal of a tree, a binary tree is constructed.
Note: you can assume that there are no duplicate elements in the tree.
For example, give
preorder traversal= [3,9,20,15,7] inorder = [9,3,15,20,7] returns the following binary tree:

4.1 ideas
This question is the same as 106. I'll just give the code. The C + + code of the logged version is as follows: (the logged version is only used for debugging. Do not submit it on leetcode. It will timeout)
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
if (preorderBegin == preorderEnd) return NULL;
int rootValue = preorder[preorderBegin]; // Be careful to use preorderBegin instead of 0
TreeNode* root = new TreeNode(rootValue);
if (preorderEnd - preorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Cut ordered array
// Middle order left interval, left closed right open [leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// Middle order right interval, left closed right open [rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// Cut preamble array
// Pre order left interval, left closed right open [leftPreorderBegin, leftPreorderEnd)
int leftPreorderBegin = preorderBegin + 1;
int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // The ending position is the starting position plus the size of the middle order left interval
// Preorder right interval, left closed right open [rightPreorderBegin, rightPreorderEnd)
int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
int rightPreorderEnd = preorderEnd;
cout << "----------" << endl;
cout << "leftInorder :";
for (int i = leftInorderBegin; i < leftInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "rightInorder :";
for (int i = rightInorderBegin; i < rightInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "leftPreorder :";
for (int i = leftPreorderBegin; i < leftPreorderEnd; i++) {
cout << preorder[i] << " ";
}
cout << endl;
cout << "rightPreorder :";
for (int i = rightPreorderBegin; i < rightPreorderEnd; i++) {
cout << preorder[i] << " ";
}
cout << endl;
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, preorder, leftPreorderBegin, leftPreorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (inorder.size() == 0 || preorder.size() == 0) return NULL;
return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
}
};
105. The binary tree is constructed by traversing the sequence from the front order to the middle order. The last version, C + + Code:
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
if (preorderBegin == preorderEnd) return NULL;
int rootValue = preorder[preorderBegin]; // Be careful to use preorderBegin instead of 0
TreeNode* root = new TreeNode(rootValue);
if (preorderEnd - preorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Cut ordered array
// Middle order left interval, left closed right open [leftInorderBegin, leftInorderEnd)
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
// Middle order right interval, left closed right open [rightInorderBegin, rightInorderEnd)
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// Cut preamble array
// Pre order left interval, left closed right open [leftPreorderBegin, leftPreorderEnd)
int leftPreorderBegin = preorderBegin + 1;
int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // The ending position is the starting position plus the size of the middle order left interval
// Preorder right interval, left closed right open [rightPreorderBegin, rightPreorderEnd)
int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
int rightPreorderEnd = preorderEnd;
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, preorder, leftPreorderBegin, leftPreorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (inorder.size() == 0 || preorder.size() == 0) return NULL;
// Parameters adhere to the principle of left closing and right opening
return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
}
};
5, Thinking questions
The preamble and the middle order can uniquely determine a binary tree. The postsequence and the middle order can uniquely determine a binary tree. Can the preamble and the rear order uniquely determine a binary tree? The preamble and the rear order cannot uniquely determine a binary tree! Because without the middle order traversal, the left and right parts cannot be determined, that is, they cannot be divided.
For example:
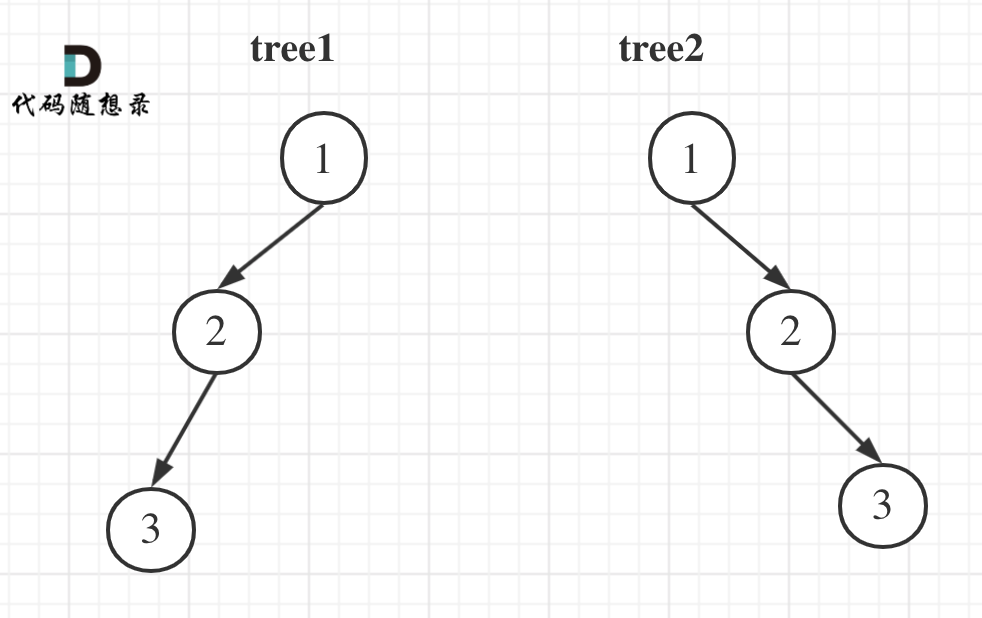
The preorder traversal of tree1 is [1 2 3], and the postorder traversal is [3 2 1].
The preorder traversal of tree2 is [1 2 3], and the postorder traversal is [3 2 1].
So the pre order and post order of tree1 and tree2 are exactly the same. Is this a tree? It's obviously two trees!
Therefore, the pre order and post order cannot uniquely determine a binary tree!
6, Summary
- The binary tree topics we talked about before are all kinds of traversal binary trees. This time, we start to construct binary trees. The idea is actually relatively simple, but it is not easy to realize the real code. Therefore, we should avoid high vision and low hand and write the code down-to-earth.
- At the same time, I gave the code version of adding logs, because this topic is not easy to write, and you can adjust it. Therefore, you must type the process log to see if it conforms to your own ideas.
- When you encounter this problem, you should also learn to log to debug (how to log is sometimes a technical activity). Don't use brain movement simulation. Brain movement simulation is easy to get more and more confused.
- Finally, I also give why pre order and middle order can uniquely determine a binary tree, post order and middle order can uniquely determine a binary tree, but pre order and post order can't.
- After carefully studying this article, I believe you will be much clearer about the structure of binary tree.