// 0 1

        // 3 0

        // 2 0

        // 4 3

        // 4 2

        // 1 4

　　

Open u, v, outf, next array

v represents the vertex, u represents the other vertex to which the group of vertices go, outf represents the first vertex of the degree, and next represents the next vertex (please note that the number of vertices stored in next is the i-th data in the v array, which is a chain, not necessarily only one)

Start of practical operation

1 initialization (note that the initial subscript of u and v arrays is 1, and the initial subscript of next and inf arrays is 0)

Because the vertex may be 0, we make - 1 null. First, outf has no nodes, so it should be initialized to null

　　　　2.

　　　　　　1. Read in the side of 0 -- > 1

outf [0] is updated to 1, which means that there is a set of out edges about 0 in the subscript 1 of v and u, specifically 0 -- > n. I don't know. next[0] is updated to - 1, which means that there is no next edge

　　　　　　2. Read in the side of 3 -- > 0

outf [3] is updated to 2, which means that a group of outgoing edges about 3 are stored in the subscript 2 of v and u, and next[3] is updated to - 1

　　　　　　3. Read in the side of 2 -- > 0

outf [2] is updated to 3, which means that there is a set of outgoing edges about 2 in the subscript 3 of v and u, and next[2] is updated to - 1

　　　　　　4. Read in side 4 -- > 3

outf [4] is updated to 4, which means that a group of outgoing edges about 4 are stored in the subscript 4 of v and u, and next[4] is updated to - 1

　　　　　　5. Read in side 4 -- > 2

outf [4] is updated to 5, which means that a group of outgoing edges about 4 are stored in the subscript 5 of v and u, and next[5] is updated to 4

　　　　　　6. Read in side 1 -- > 4

outf [1] is updated to 6, which means that there is a set of outgoing edges about 1 in the subscript 6 of v and u, and next[1] is updated to - 1

The processed chart is

　　　　　　

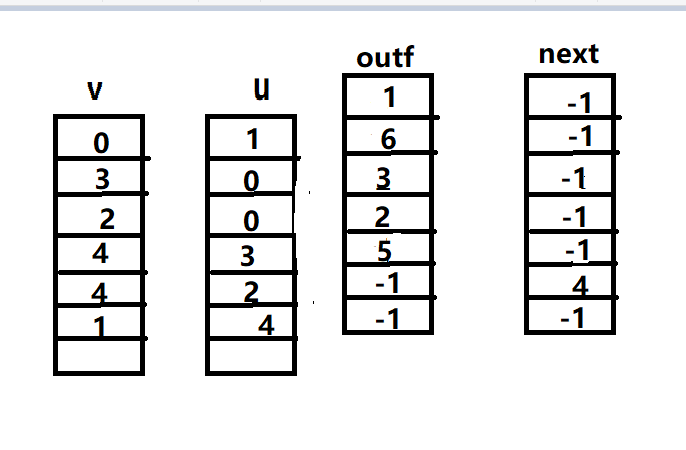
III. inverse adjacency table

The idea of inverse adjacency table is the same as that of adjacency table. Inverse adjacency table is used to calculate the in degree of a point, while adjacency table is used to calculate the out degree of a point.

4, Code implementation

 1 #include "bits/stdc++.h"
 2 using namespace std;
 3 int inf[110],outf[110];
 4 int inext[110],outnext[110];//in Represents penetration, out Representative degree
 5 int v[110],u[110];
 6 int main()
 7 {
 8     for(int i = 1;i <= 100;i++)
 9         inf[i] = -1,outf[i] = -1;
10     int n,m;
11     cin >> n >> m;//n It's the top point, m Is the number of sides
12     int vi,ui;
13     for(int i = 1;i <= m;i++){
14         cin >> v[i] >> u[i];//vi-->ui It's out, ui-->vi It's penetration
15         outnext[i] = outf[v[i]];//outf An adjacency table is created
16         outf[v[i]] = i;
17         inext[i] = inf[u[i]];//inf An inverse adjacency table is established
18         inf[u[i]] = i;
19     }
20     for(int i = 1;i <= n;i++){
21         int ink,outk;
22         ink = inf[i];
23         outk = outf[i];
24         if(ink != -1)
25             cout << u[ink] << "\nin:" << endl;
26         //Yidi i The edge whose node No. is in degree is
27         while(ink != -1){
28             cout << v[ink] << "-->" << u[ink] << endl;
29             ink = inext[ink];
30         }
31         if(outk != -1)
32             cout << "out:" << endl;
33         //Yidi i The edge with node No. as out degree is
34         while(outk != -1){
35             cout << v[outk] << "-->" << u[outk] << endl;
36             outk = outnext[outk];
37         }
38         cout << "\n\n";
39     }
40     return 0;
41 }