What is an adapter
adapters play the role of bearing and converter in the flexible combination and application function of STL components. The concept of adapter is actually a design pattern. In the design pattern, the definition of adapter style is as follows: convert one class interface into another class interface, so that classes that are incompatible with the original interface and cannot cooperate can operate together.
use
1. container adapters applied to containers, such as stack and queue, are actually an adapter. They create another container style by modifying the interface of deque.
2. Apply to iterator adapters
3. Applied to imitative function
Container adapter
container adapters applied to containers, such as stack and queue, are actually an adapter. They create another container style by modifying the interface of deque.
Common container adapters
For example, stack and queue are encapsulated structures based on deque (double ended queue)
Container adapter – queue
A Queue is a first in first out (FIFO) linear table. It only allows insertion at one end of the table and deletion at the other end. Inserting an element into a Queue is called enqueue, and deleting an element from a Queue is called dequeue.
2) The end of the front that allows deletion is called the front.
2) The end at which insertion is allowed is called the end of the queue.
4) The length of the queue the number of data elements in the queue represents the length of the queue.
5) An empty queue is called an empty queue when there are no elements in the queue.
6) The modification of first in first out table (FIFO) queue is based on the principle of first in first out, also known as first in first out table (FIFO)
Common interface test
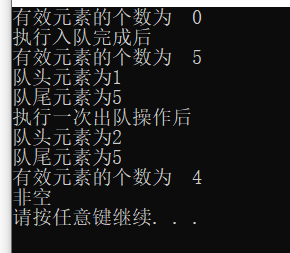
void test()
{
//Test structure
queue<int>vv1;
cout << "The number of valid elements is ";
cout << vv1.size() << endl;
vv1.push(1);
vv1.push(2);
vv1.push(3);
vv1.push(4);
vv1.push(5);
cout << "After the execution is completed" << endl;
cout << "The number of valid elements is ";
cout << vv1.size() << endl;
cout << "The team head element is" << vv1.front() << endl;
cout << "The tail element is" << vv1.back() << endl;
//Out of line operation
vv1.pop();
cout << "After performing an out of line operation" << endl;
cout << "The team head element is" << vv1.front() << endl;
cout << "The tail element is" << vv1.back() << endl;
cout << "The number of valid elements is ";
cout << vv1.size() << endl;
if (vv1.empty())
{
cout << "empty" << endl;
}
else
{
cout << "Non empty" << endl;
}
}
Analog implementation queue
namespace bite
{
template<class T, class Container = std::deque<T>>
class queue
{
public:
queue()
{}
void push(const T& data)
{
c.push_back(data);
}
void pop()
{
c.pop_front();
}
T& front()
{
return c.front();
}
const T& front()const
{
return c.front();
}
T& back()
{
return c.back();
}
const T& back()const
{
return c.back();
}
size_t size()const
{
return c.size();
}
bool empty()const
{
return c.empty();
}
private:
Container c;
};
}
Container adapter – stack
Definition: a "special" linear data structure that can only be operated at one end. The operable end is called the top of the stack and the other end is called the bottom of the stack.
Feature: last in first out
Common interface test

structure
//Test structure
void test_constructor()
{
deque<int>mycp1(2, 100);
vector<int>mycp2(3, 100);
//Nonparametric structure
stack<int>vv1;
//When copying a construct and no explicit declaration is provided, only deque objects can be constructed.
stack<int>vv2(mycp1);
//The storage type is explicitly given
stack<int, vector<int>>vv3(mycp2);
cout << vv1.size() << endl;
cout << vv2.size() << endl;
cout << vv3.size() << endl;
}

Size() method, top() method, size() method, pop() method, push() method
void test()
{
stack<int>vv1;
if (vv1.empty())
{
cout << "Stack empty" << endl;
}
else
{
cout << "Stack is not empty" << endl;
}
vv1.push(10);
vv1.push(20);
vv1.push(30);
vv1.push(40);
cout << "vv1 The number of valid elements at this time is" << vv1.size() << endl;
cout << "vv1 The top element of the stack is" << vv1.top() << endl;
vv1.pop();
cout << "After stack out operation" << endl;
cout << "vv1 The number of valid elements at this time is" << vv1.size() << endl;
cout << "vv1 The top element of the stack is" << vv1.top() << endl;
}

Simulation implementation stack
namespace mystack
{
// Container: the type of container that stores elements at the bottom of the stack,
template<class T, class Container = std::deque<T>>
class stack
{
public:
stack()
: c()
{}
void push(const T& data)
{
c.push_back(data);
}
void pop()
{
if (c.empty())
return;
c.pop_back();
}
T& top()
{
return c.back();
}
const T& top()const
{
return c.back();
}
size_t size()const
{
return c.size();
}
bool empty()const
{
return c.empty();
}
private:
Container c;
};
}
priority_queue priority queue

Common method test
//Structure
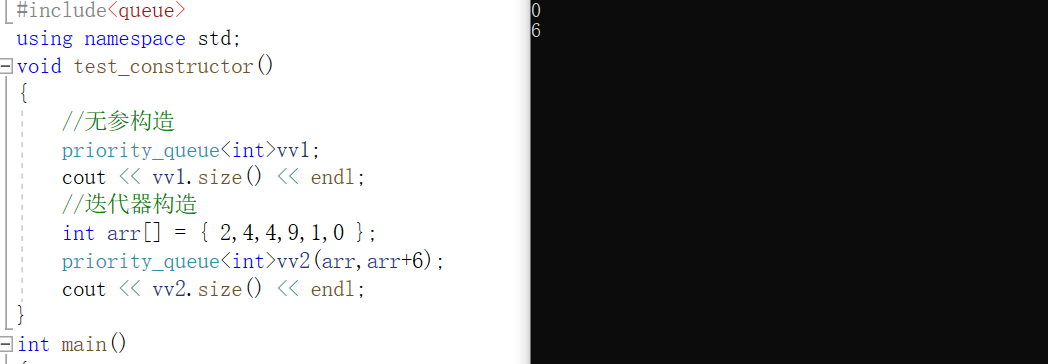
void test_constructor()
{
//Nonparametric structure
priority_queue<int>vv1;
cout << vv1.size() << endl;
//Iterator construction
int arr[] = { 2,4,4,9,1,0 };
priority_queue<int>vv2(arr,arr+6);
cout << vv2.size() << endl;
}
void test_push_top()
{
priority_queue<int>vv1;
vv1.push(1);
vv1.push(5);
vv1.push(2);
vv1.push(9);
vv1.push(4);
cout << "The number of valid elements is" << vv1.size() << endl;
cout << "The heap top element is" << vv1.top() << endl;
vv1.pop();
cout << "The number of valid elements is" << vv1.size() << endl;
cout << "The heap top element is" << vv1.top() << endl;
if (vv1.empty())
{
cout << "Priority queue is empty" << endl;
}
else
{
cout << "Priority queue is not empty" << endl;
}
}

Simulation Implementation
namespace my
{
template<class T, class container = std::vector<T>, class compare = std::less<T>>
//template<class T, class Container = std::vector<T>, class Compare = std::less<T>>
class priority_queue
{
public:
priority_queue()
{}
template<class Iterator>
priority_queue(Iterator first, Iterator last)
: c(first, last)
{
int root = ((c.size() - 1 - 1) >> 1);
for (; root >= 0; root--)
AdjustDown(root);
}
void push(const T& t1)
{
c.push_back(t1);
AdjustUp();
}
void pop()
{
if (empty())
{
return;
}
std::swap(c.front(), c.back());
c.pop_back();
AdjustDown(0);
}
const T& top()const
{
return c.front();
}
size_t size()const
{
return c.size();
}
bool empty()const
{
return c.empty();
}
private:
void AdjustDown(int root)
{
int child = root * 2 + 1;
int size = c.size();
while (child < size)
{
if (child + 1 < size && com(c[child], c[child + 1]))
{
child += 1;
}
if(com(c[root],c[child]))
{
std::swap(c[root], c[child]);
root = child;
child = 2 * root + 1;
}
else
{
return;
}
}
}
void AdjustUp()
{
int child = c.size() - 1;
int parent = ((child - 1) >> 1);
while (child)
{
if (com(c[parent], c[child]))
{
std::swap(c[parent], c[child]);
child = parent;
parent = ((child - 1) >> 1);
}
else
{
return;
}
}
}
private:
container c;
compare com;
};
}
#include<iostream>
using namespace std;
void TestMyPriorityQueue()
{
int array[] = { 5,6,3,0,9,2,8,1,7,4 };
my::priority_queue<int, vector<int>, less<int>> q(array, array + sizeof(array) / sizeof(array[0]));
cout << q.top() << endl;
q.pop();
cout << q.top() << endl;
cout << q.size() << endl;
}
deque double ended queue
concept
Deque (double ended queue): it is a data structure of "continuous" space with double openings. The meaning of double openings is that insertion and deletion can be carried out at both ends of the head and tail, and the time complexity is O(1). Compared with vector, the head insertion efficiency is high, and there is no need to move elements; Compared with list, the space utilization rate is relatively high
Deque is not really a continuous space, but is composed of small continuous spaces. The actual deque is similar to a dynamic two-dimensional array
The bottom layer of the double ended queue is an imaginary continuous space, which is actually piecewise continuous. In order to maintain its "overall continuity" and the illusion of random access, it falls on the iterator of deque
Access to dual ended queue elements - a brief introduction
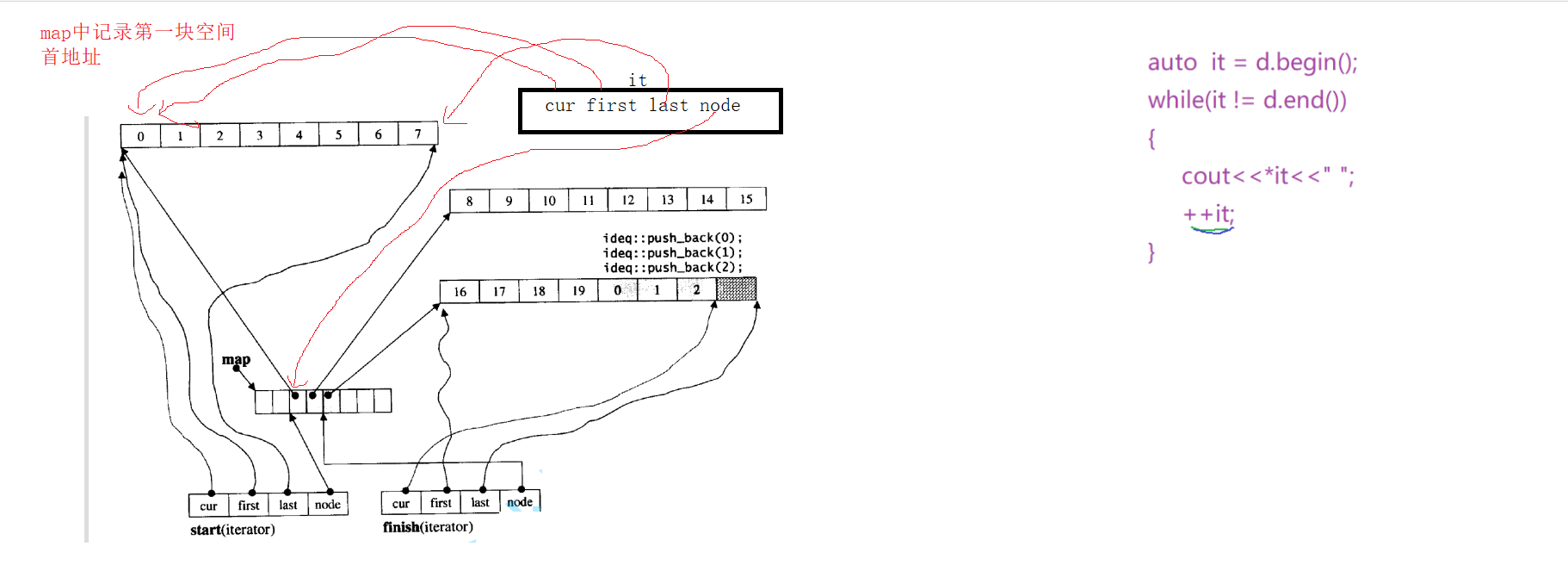
Advantages and disadvantages of two terminal queue
Compared with vector, deque has the following advantages: it does not need to move elements during header insertion and deletion, which is particularly efficient. Moreover, it does not need to move a large number of elements during capacity expansion, so its efficiency must be high. Compared with list, its bottom layer is continuous space, which has high space utilization and does not need to store additional fields. However, deque has a fatal defect: it is not suitable for traversal, because during traversal, the iterator of deque needs to frequently detect whether it moves to the boundary of a small space, resulting in low efficiency. In sequential scenes, it may need to be traversed frequently. Therefore, in practice, when linear structure is required, vector and list are given priority in most cases, and deque is not widely used, One application that can be seen at present is that STL uses it as the underlying data structure of stack and queue
Why use deque as the underlying implementation of stack and queu
- Stack and queue do not need to be traversed (so stack and queue have no iterators), but only need to operate at one or both ends of the fixed end.
- When the elements in stack grow, deque is more efficient than vector (there is no need to move a large amount of data during capacity expansion); When the elements in the queue grow, deque is not only efficient, but also has high memory utilization.