catalogue
2.3 simulation implementation of stack
3.3 simulation implementation of queue
IV priority_queue priority queue
4.1priority_queue introduction
4.3 simulation implementation of priority queue
I What is a container Adapter
Container adapter is a class template that encapsulates the sequence container. It provides some different functions based on the general sequence container. It is called container adapter because it is an adapter container to provide other different functions. The functions we need are realized through the corresponding container and member functions.
The following describes three container adapters: STATK < T >, queue < T >, and priority_ queue<T>.
Note: no container adapter has an iterator.
II Stack stack
2.1 introduction to stack

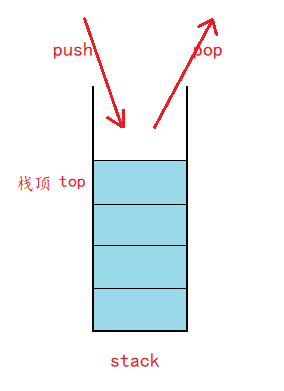
- Stack is a last in first out container adapter. Its deletion and insertion can only be performed at one end of the container. That is, you can only insert and pop up at the top of the stack.
- The underlying container of stack can be any standard container class template or other specific class containers (containers designed by you), but these containers must support the following operations: empty, back and push_ Back, pop_ Back (tail deletion), size (get element size).
- vector, list and deque can be used as the underlying container of stack. By default, if no container is specified for stack, deque is used as the default container by default.
2.2 use of stack
| Function name | function |
| stack() | Construct an empty stack |
| empty() | Judge whether the stack is empty. If it is empty, it returns true, and if it is not empty, it returns false |
| size() | Returns the number of stack elements |
| top() | Returns a reference to the top element of the stack |
| push() | Insert element at top of stack |
| pop() | Pop up stack top element |
Using stack requires the header file #include < stack >, and stack does not have an iterator.

2.3 simulation implementation of stack

#include<iostream>
#include<deque>
#include<vector>
#include<list>
using namespace std;
namespace my{
template<class T,class Container=deque<T>>
class stack{
public:
bool empty(){
return _con.empty();
}
size_t size(){
return _con.size();
}
T& top(){
return _con.back();
}
const T& top()const{
return back();
}
void push(const T& val){
_con.push_back(val);
}
void pop(){
_con.pop_back();
}
private:
Container _con;
};
void test_stack(){
stack<int> s;
s.push(1);
s.push(2);
s.push(3);
s.push(4);
while (!s.empty())
{
cout << s.top() << " ";
s.pop();
}
cout << endl;
}
void test_stack1(){
stack<int,list<int>> s;
s.push(1);
s.push(2);
s.push(3);
s.push(4);
while (!s.empty())
{
cout << s.top() << " ";
s.pop();
}
cout << endl;
}
}III Queue queue
3.1 queue introduction

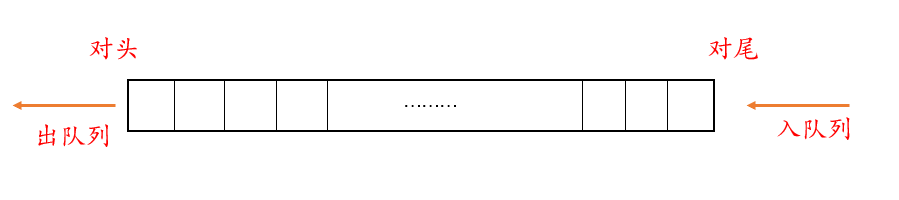
- A queue is a first in, first out container adapter in which elements are inserted from one end of the container and extracted from the other end. Insert at the end of the queue and pop up elements at the opposite end.
- The underlying container is one of the standard container class templates. You can also use only the container class specially designed by you. The container must support empty, front, back and push_ Back, pop_ Front (header deletion), size (get element size).
- vector, list and deque meet these requirements. By default, the container specified by queue is not displayed, and deque is used by default.
3.2 use of queue
| Function declaration | Function introduction |
| queue() | Construct an empty queue |
| size() | Returns the number of elements in the queue |
| empty() | Determine whether the queue is empty |
| back() | Returns the end of queue element reference |
| front() | Returns the queue header element reference |
| push() | Insert element at end |
| pop() | Pop up the team head element |
The header file #include < queue > is required to use queue. The queue container adapter does not have an iterator

3.3 simulation implementation of queue
Because there are header deletion and tail insertion in the queue, it is too inefficient to use the vector container to encapsulate. The header deletion needs to move the data, and the vector does not provide pop_front(), because the efficiency is too low.
#pragma once
#include<iostream>
#include<deque>
#include<vector>
#include<list>
using namespace std;
namespace my{
template<class T, class Container = deque<T>>
class queue{
public:
//The container constructor is called
queue(){};
//Notice the implicit this pointer
size_t size()const{
return _con.size();
}
bool empty()const{
return _con.empty();
}
T& back(){
return _con.back();
}
T& front(){
return _con.front();
}
const T& back()const{
return _con.back();
}
const T& front()const{
return _con.front();
}
void push(const T& val){
_con.push_back(val);
}
void pop()
{
_con.pop_front();
}
private:
Container _con;
};
void test_queue1(){
queue<int> q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
cout << q.size() << endl;
cout << q.back() << endl;
cout << q.front() << endl;
while (!q.empty()){
cout << q.front() << " ";
q.pop();
}
cout << endl;
}
}IV priority_queue priority queue
4.1priority_queue introduction

- A priority queue is a container adapter whose first element always has the highest priority among the elements it contains according to the sorting criteria. (perhaps the value is the largest or the smallest), just like the heap in a data structure.
- Priority queues are formed by default
- The elements of the priority queue pop up from the top, which is the highest priority.
- The underlying container can be the class template of any container or other specially designed container classes (self-designed). The functions supported by the container are random access operator [], empty, size, front and push_back,pop_front.
- Both standard container vector and deque can meet these requirements. When the container template is not displayed and defined, the priority queue uses vector by default.
- Priority queues use affine functions to control whether large or small root heaps are generated.
Let's briefly introduce the imitation function:
Functor, also known as Function Object, is a class that can perform function functions. The syntax of the functor is almost the same as that of our ordinary function calls, but as the class of the functor, the operator() operator must be overloaded. Because calling an imitation function is actually calling the overloaded operator() operator through a class object. A functor is a class that just looks like a function. We'll know when the simulation is implemented.
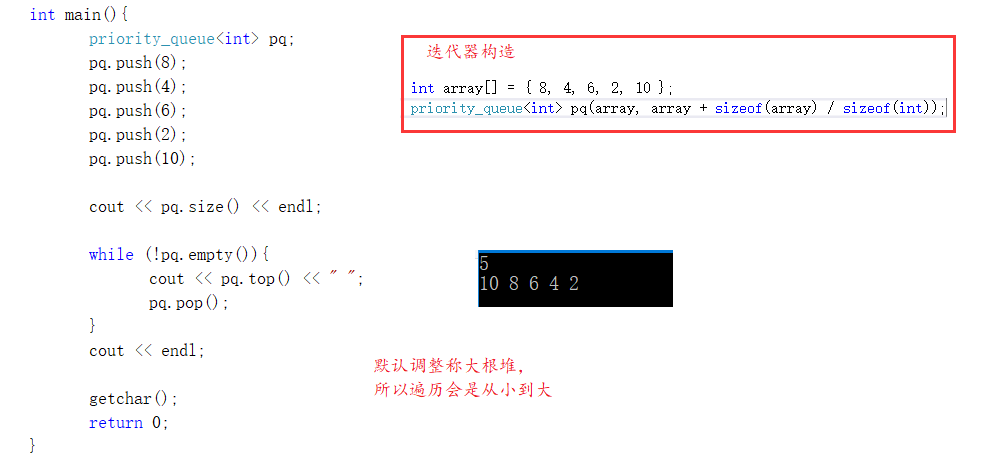
4.2 priority_queue usage
By default, the priority queue uses the vector as the container for storing data. Based on the container, the heap algorithm is used to adjust the elements in the vector into a heap structure.
Note: the priority queue is a heap. The priority queue can be used wherever the heap is used. A large root heap is generated by default, and the header file is also #include < queue >
| function | function |
| priority_queue() | Create an empty priority queue |
| priority_queue(first,last) | Heap the elements between the iterators first and last |
| top | Returns the highest priority element in the priority queue, that is, the top element of the heap |
| size | Returns the number of elements in the priority queue |
| empty | Determine whether the priority queue is empty |
| push | Insert element into priority queue |
| pop | Delete the highest priority element in the priority queue, that is, the heap top element |
Note: if in priority_ The data types to be overloaded are called < queue > and placed in the heap.
4.3 simulation implementation of priority queue
Review the heap insert and delete operations.
Heap insertion: insert data at the end of the heap, and then adjust it upward into a heap.
Delete the heap: exchange the top elements of the heap with the tail elements, and then adjust them downward into a heap.
Without affine function:
Adjustment function:

#pragma once
#include<iostream>
#include<deque>
#include<vector>
#include<list>
using namespace std;
namespace my{
template<class T,class Container = vector<T>>
class priority_queue{
public:
priority_queue(){};
template<class inputiterator>
priority_queue(inputiterator first, inputiterator last){
while (first != last){
push(*first);
first++;
}
}
bool empty(){
return _con.empty();
}
size_t size(){
return _con.size();
}
T& top(){
return _con.front();
}
const T& top()const{
return _con.front();
}
void push(const T& val){
_con.push_back(val);
Adjustup(_con.size() - 1);
}
void pop(){
swap(_con[0], _con[_con.size() - 1]);
//The missing element is size subtraction. After the exchange, the last element is deleted directly
_con.pop_back();
Adjustdown(0);
}
private:
void Adjustup(int child){
int parent = (child - 1) / 2;
while (child > 0){
if (_con[child] > _con[parent]){
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else{
break;
}
}
}
void Adjustdown(int parent){
int child = parent * 2 + 1;
//Cannot subtract 1. If no element size() is 0, the type size_t. Minus 1 is the maximum number (positive number) and will enter the loop
while ((size_t)child < _con. size() ){
if (child + 1 < _con.size() && _con[child + 1] > _con[child]){
child++;
}
if (_con[child]>_con[parent]){
swap(_con[child], _con[parent]);
parent = child;
child = parent * 2 + 1;
}
else{
break;
}
}
}
Container _con;
};
void test_priority_queue(){
int array[] = { 8, 4, 6, 2, 10 };
priority_queue<int> pq(array, array + sizeof(array) / sizeof(int));
cout << pq.size() << endl;
while (!pq.empty()){
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
}
}Imitation function: priority queue is realized by imitation function to establish large root heap or small root heap.
To adjust whether to create a large root heap or a small root heap, you only need to change the adjustment function. The greater than or less than sign when comparing the parent node with the child node. How to realize it by imitating function?

How to modify the adjustment function:

#pragma once
#include<iostream>
#include<deque>
#include<vector>
#include<list>
using namespace std;
namespace my{
template<class T>
struct less{
bool operator()(const T& left,const T& right){
return left < right;
}
};
template<class T>
struct greater{
bool operator()(const T& left, const T& right){
return left>right;
}
};
template<class T,class Container = vector<T>,class Compare=less<T>>
class priority_queue{
public:
priority_queue(){};
template<class inputiterator>
priority_queue(inputiterator first, inputiterator last){
while (first != last){
push(*first);
first++;
}
}
bool empty(){
return _con.empty();
}
size_t size(){
return _con.size();
}
T& top(){
return _con.front();
}
const T& top()const{
return _con.front();
}
void push(const T& val){
_con.push_back(val);
Adjustup(_con.size() - 1);
}
void pop(){
swap(_con[0], _con[_con.size() - 1]);
//The missing element is size subtraction. After the exchange, the last element is deleted directly
_con.pop_back();
Adjustdown(0);
}
private:
void Adjustup(int child){
int parent = (child - 1) / 2;
Compare com;
while (child){
if (com(_con[parent],_con[child])){
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else{
break;
}
}
}
void Adjustdown(int parent){
int child = parent * 2 + 1;
//Define an object
Compare com;
//Cannot subtract 1. If no element size() is 0, the type size_t. Minus 1 is the maximum number (positive number) and will enter the loop
while ((size_t)child < _con. size() ){
if (child + 1 < _con.size() && com(_con[child], _con[child + 1])){
child++;
}
if (com(_con[parent], _con[child])){
swap(_con[child], _con[parent]);
parent = child;
child = parent * 2 + 1;
}
else{
break;
}
}
}
Container _con;
};
void test_priority_queue(){
int array[] = { 8, 4, 6, 2, 10 };
priority_queue<int,vector<int>,greater<int>> pq(array, array + sizeof(array) / sizeof(int));
cout << pq.size() << endl;
while (!pq.empty()){
cout << pq.top() << " ";
pq.pop();
}
cout << endl;
}
}