catalogue

Realizing queue force deduction 232 questions with stack

Realizing stack force deduction 225 questions with queue

1. Dual queue implementation stack

2. A queue implementation stack

The essence of stack and queue is the same. They can only be inserted and deleted at one end of the linear table. Therefore, the stack and queue can be converted to each other.

Realizing queue force deduction 232 questions with stack

Topic requirements: only two stacks are used to realize the first in first out queue. The queue should support all operations supported by the general queue

Using dual stacks to implement queues, we can make one stack store specific elements and the other stack assist

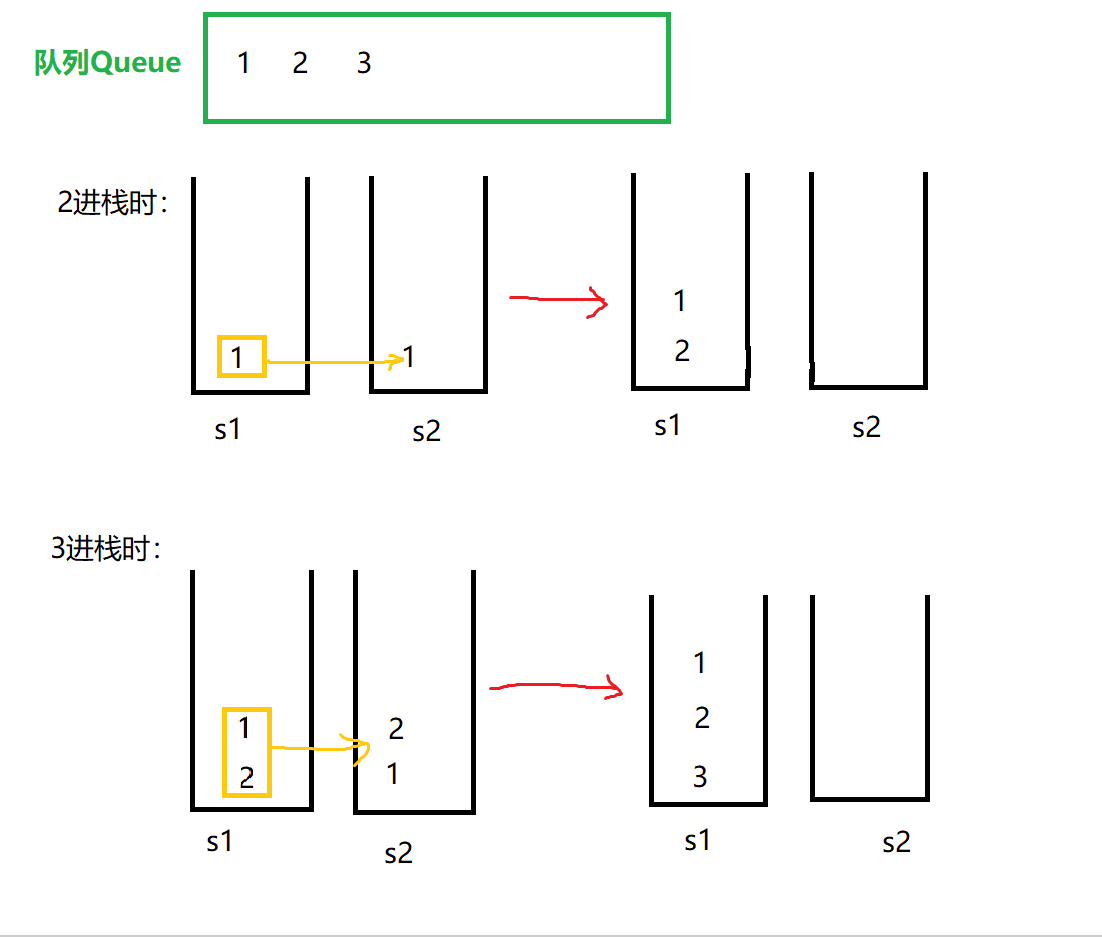As can be seen from the above figure, when a new element enters the stack, make sure that the stack is empty. The elements entering the stack are stored in the auxiliary stack in order. After the new elements enter the stack, the elements in the auxiliary stack are listed in order. After this operation, the elements in the stack are stored in the same order as those in the queue

Code implementation:

//Dual stack simulation queue
public class MyQueue{
    //Stack of actual storage elements
    private Stack<Integer> s1 = new Stack<>();
    //Auxiliary stack
    private Stack<Integer> s2 = new Stack<>();

    public MyQueue() {

    }

    //Push element x to the end of the queue
    public void push(int x) {
        if (s1.empty()){//If the stack is empty, put it directly into x
            s1.push(x);
        }else {
            //Not empty at this time
            //First pop all s1 elements into s2
            while (!s1.empty()){
                s2.push(s1.pop());//The value put in by s2 is the value popped out by s2
                //The following two sentences are the same as the previous one
//                int val = s1.pop();
//                s2.push(val);
            }
            //Put the new element directly into s1, and the new element is at the top of the stack of s1
            s1.push(x);
            //Pop up all the values of s2 and put them into s1 in turn again
            while (!s2.empty()){
                s1.push(s2.pop());
            }
        }

    }

    //Removes and returns an element from the beginning of the queue
    public int pop() {
       return s1.pop();
    }

    //Returns the element at the beginning of the queue
    public int peek() {
        return s1.peek();
    }

    //Judge whether the queue is empty
    public boolean empty() {
        return s1.empty();
    }
}

Realizing stack force deduction 225 questions with queue

Title Requirements: only two queues are used to realize a last in first out (LIFO) stack, and all four operations of ordinary stack are supported

1. Dual queue implementation stack

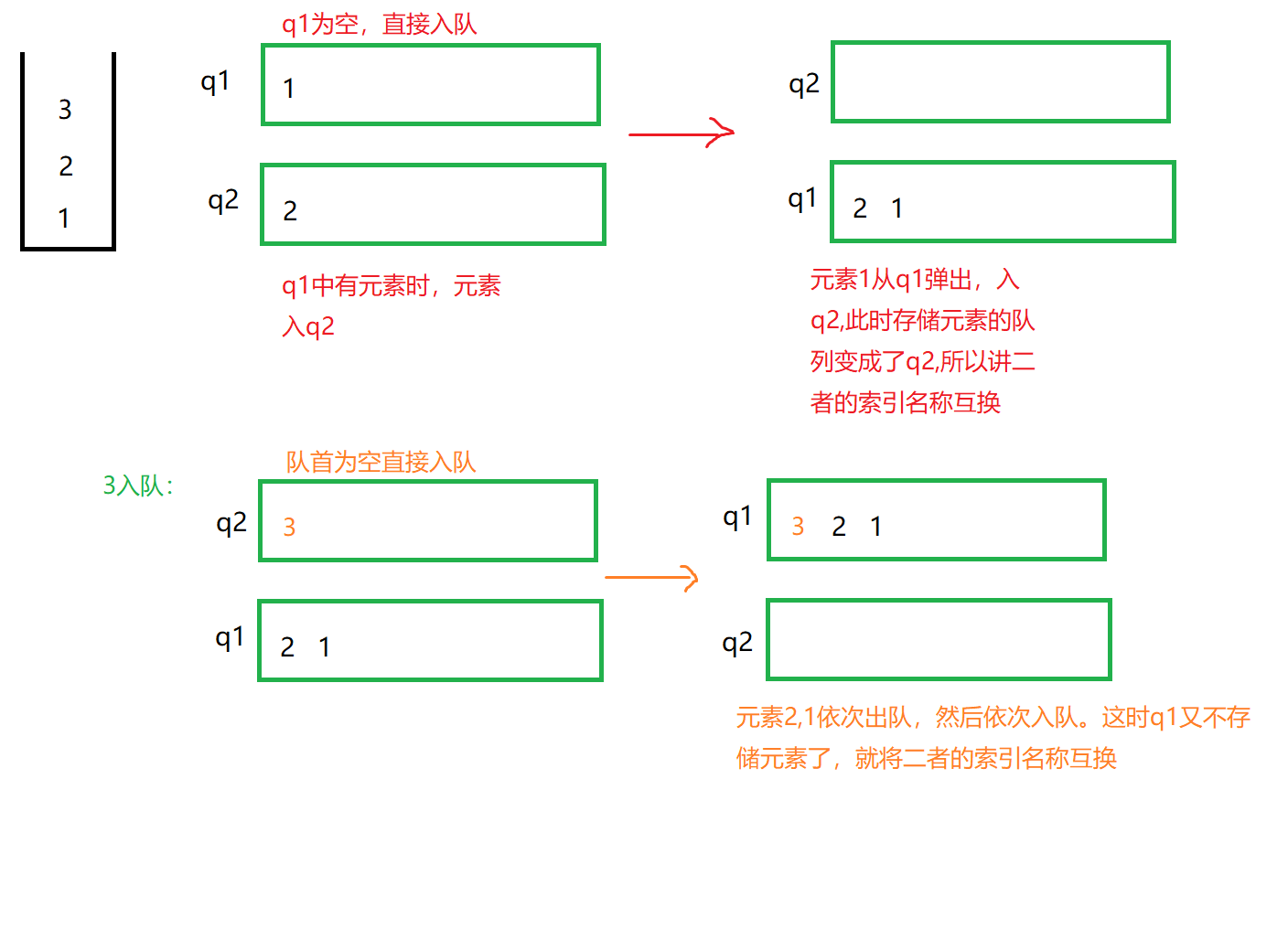
The stack is realized by using double queues. q1 is the queue for storing elements, which ensures that q2 will always be an empty queue after adding elements (new elements directly enter q2), so as to ensure that new elements are at the head of the queue. In this way, after the new elements join the queue, the elements of another queue will leave the queue and then join the queue in turn, so as to realize a stack.

Code implementation:

public class MyStack {
    //q1 is the queue where the elements are stored
    private Queue<Integer> q1 = new LinkedList<>();
    //Yes, secondary queue q2
    //Ensure that q2 is always empty after adding elements
    private Queue<Integer> q2 = new LinkedList<>();
    public MyStack () {

    }

    //Push element x to the top of the stack
    public void push(int x) {
        //New team elements enter q2 directly and become the leader of q2 team
        q2.offer(x);
        //Dequeue all elements in q1 in turn and enter q2
        while (!q1.isEmpty()){
            q2.offer(q1.poll());
        }

        //q1 is empty, q2 is the queue of storage elements, and the exchange reference points to
        //After the exchange, q1 is still the queue for storing elements, and q2 is empty
        Queue<Integer> temp = q1;
        q1 = q2;
        q2 = temp;
    }

    // Remove and return stack top element
    public int pop() {
        return q1.poll();
    }

    //Return stack top element
    public int top() {
        return q1.peek();
    }

    //Determine whether the stack is empty
    public boolean empty() {
        return q1.isEmpty();
    }
}

2. A queue implementation stack

First put the elements into the team, then put the previous elements out of the team in turn, and then enter the team! In other words, ensure that new elements are at the head of the team

Code implementation:

public class MyStack {
    private Queue<Integer> queue = new LinkedList<>();
    public MyStack() {
    }

    public void push(int x) {
        //Number of elements before recording
        int size = queue.size();
        //Add new elements to the team
        queue.offer(x);
        //Take the previous elements out of the team and then into the team, and the new element is at the head of the team
        for (int i = 0; i < size; i++) {
            queue.offer(queue.poll());
        }

    }

    public int pop() {
        return queue.poll();
    }

    public int top() {
        return queue.peek();
    }

    public boolean empty() {
        return queue.isEmpty();
    }
}

The purpose of these examples is to be more familiar with the stack and queue. It is not recommended in practical application.