1, Critical path algorithm

Critical path algorithm is to find out several key activities when the project can be completed, so as to achieve the effect of completing the project earlier.

2, Algorithm analysis

In this algorithm, we need to use the variables etv, ltv, ete and lte, as well as the algorithm to ensure the completion of the project, that is, the topological sorting algorithm

In this algorithm, we regard vertices as events, edge weights as activity duration, and edges as activities

Explain the meaning of these variables, etv and ltv (i.e. the earliest start time and the latest start time of the event)

ete, lte (i.e. the earliest start time and the latest start time of the activity)

3, Algorithm steps

　　1. Use topological sorting to find out whether the critical path can be queried

　　2. In the process of topological sorting, the earliest start time of events is calculated

　　3. The stack is used to store the topology sequence, and then the latest start time of events is pushed from the top of the stack

　　4. Use ete and lte to judge whether this activity is a key activity

　　5.ete is equal to the earliest start time of this event (why? Because if you want this event to happen, you must wait for all the previous things to happen, so it is the solution step of the earliest start time)

　　6.lte is equal to the latest start time of the next event minus the duration (why? Because the latest start time of the next event represents whether the subsequent events can be carried out normally, that is, whether the subsequent activities can be carried out. Similarly, the latest start time of the activity should also be the latest start time duration of the next event)

4, Code implementation

 1 #include "bits/stdc++.h"
 2 using namespace std;
 3 int etv[110],ltv[110];//etv Is the earliest start of the event, ltv Is the latest start event of the event
 4 int indegree[110];//Record the penetration of a vertex
 5 int u[110],v[110],w[110];//Establish adjacency table
 6 int first[110],outnext[110];
 7 stack <int> Topo;
 8 int n,m;
 9 void TopologicalSort()//Sort topology
10 {
11     int cnt = 0;
12     queue <int> ans;
13     for(int i = 1;i <= n;i++)
14         if(!indegree[i])//Put the points with a penetration of 0 into the queue
15             ans.push(i);
16     while(!ans.empty()){
17         int v1 = ans.front();
18         ans.pop();
19         Topo.push(v1);//Put the topologically sorted sequence into the stack to pave the way for solving the latest event start event later
20         cnt++;
21         int k =  first[v1];//Traverse all his edges
22         while(k != -1){
23             if(!(--indegree[u[k]]))//Points with statistical penetration of 0 are added to the topological sequence
24                 ans.push(u[k]);
25             etv[u[k]] = max(etv[u[k]],etv[v1] + w[k]);//Why is the maximum value required to solve the earliest start time of an event? Because you need to ensure that all the previous events have ended, you can only count the longest time in the first few
26             k = outnext[k];
27         }
28     }
29     if(cnt < n)//Determine whether it is a topological sequence
30         cout << "Fail" << endl;
31     else 
32         cout << "Successful!" << endl;
33 }
34 void CriticalPathMethod()
35 {   
36     TopologicalSort();//Sort topology
37     for(int i = 1;i <= n;i++)//because ltv Is to find the minimum value, then the maximum in this array must also be etv The largest in the, which will not affect ltv Solution of the value of
38         ltv[i] = etv[n];
39     while(!Topo.empty()){//Solve from the sink point (end point) to the source point (starting point) ltv((latest start time)
40         int v1 = Topo.top();
41         Topo.pop();
42         int k = first[v1];
43         while(k != -1){
44             ltv[v[k]] = min(ltv[v[k]],ltv[u[k]] - w[k]);//Why min And? Because you have to make the later activities can be carried out according to the normal time, you can't use the maximum, otherwise the later projects may be affected
45             k = outnext[k];
46         }
47     }
48     int ete,lte;//ete Is the earliest start time of the activity, lte Is the latest start time of the activity. (here, activities refer to edges and events refer to vertices)
49     for(int i = 1;i <= n;i++){
50         int k = first[i];
51         while(k != -1){
52             ete = etv[i];//The earliest start time of the activity is the longest path before this, so it is the earliest start time of the event
53             lte = ltv[u[k]] - w[k];//The latest start time of the activity is the latest start time without delaying the construction period, that is, the latest occurrence time of the event-This duration (i.e. edge weight)
54             if(lte == ete)//When the earliest activity start time is equal to the latest activity start time, this activity is a key activity, and the complete set of key activities is a key path, and there may be more than one key path
55                 cout << "(" << i << ',' << u[k] << ')' << ":weight" << w[k] << endl;
56             k = outnext[k];
57         }
58     }
59 }
60 int main()
61 {
62     cin >> n >> m;
63     for(int i = 1;i <= n;i++)
64         first[i] = -1;
65     for(int i = 1;i <= m;i++){
66         cin >> v[i] >> u[i] >> w[i];
67         indegree[u[i]]++;//Penetration+1
68         outnext[i] = first[v[i]];
69         first[v[i]] = i;
70    }
71     CriticalPathMethod();
72     return 0;
73 }

V. test data

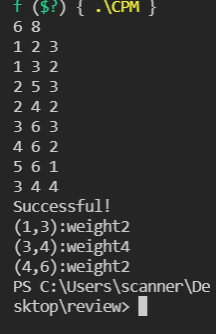
test case1　

6 8
1 2 3
1 3 2
2 5 3
2 4 2
3 6 3
4 6 2
5 6 1
3 4 4

answer1

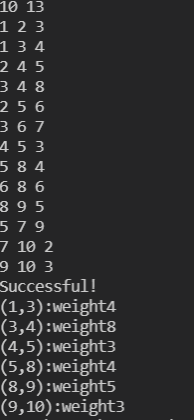
test case2:

10 13
1 2 3
1 3 4
2 4 5
3 4 8
2 5 6
3 6 7
4 5 3
5 8 4
6 8 6
8 9 5
5 7 9
7 10 2
9 10 3

answer2