Hello, everyone. Meet again. I'm Jun Quan.

introduction

Ray has many important applications in 3D graphics. For example, pick operation is realized by ray ray, and ray ray can be used for collision detection of bullet ray.

Therefore, in this blog, we will briefly introduce it to you. How to carry out ray triangle cross detection.

Ray triangle cross detection algorithm

In Tomas Moller's MT97 paper, a new algorithm is proposed. Such an algorithm can reduce the memory consumption required for ray triangle cross detection. In the past. Ray triangle cross detection is mainly to calculate the intersection of the plane composed of ray and triangle, and then infer whether the intersection is on the triangle again. To infer whether there is a crossover.

This method is very intuitive and consistent with the mathematical knowledge we have learned all the time. However, such a detection method carries out more calculations. And we also need to find its plane according to the triangle. This requires calculation. At the same time, it is necessary to open up another space to save the calculated plane.

The beauty of mathematics is that other methods can be found to replace this obvious way, so as to simplify the problem to a certain extent. Such a simplified process. It doesn't need to be implemented in the code. We just need to calculate the final conclusion on the draft paper according to the conditions in advance. We just need to use the final conclusion directly in our code.

In Tomas Moller's paper, it mentioned this concept:

Suppose a point is in triangle V0. On V1 and V2, this point can be represented in the following way, for example:

T(u, v) = (1 – u – v) * V0 + u * V1 + v * V2 ;

Here u + V < = 1, u > = 0, V > = 0

For ray, we generally use the following equation to express it:

R (t)= O + t * D ; (O is the starting point of the ray and D is the direction of the ray)

So, since they want to have intersections. We can directly use the following methods, for example:

O + t * D = (1 – u – v) * V0 + u * V1 + v * V2

Then a series of transformations are carried out. Finally get the result.

Interested readers can read by themselves Tomas Moller's paper , the paper explains the derivation process in detail. I won't repeat it here.

Implementation of ray triangle cross detection algorithm

The following is the Moller algorithm implementation of ray triangle cross detection algorithm, which is basically a copy of the code in Tomas Moller's paper, for example:

<span style="font-family:Microsoft YaHei;">bool Ray::intersectWithTriangle(VECTOR3 v0,VECTOR3 v1, VECTOR3 v2,
			bool bCull, 
			float *t)
{
	VECTOR3 edge1, edge2, tvec, pvec, qvec ;
	float det, inv_det ;
	float u,v ;

	//Find vectors for two edges sharing vert0
	Vec3Sub(edge1, v1, v0);
	Vec3Sub(edge2, v2, v0);

	//Begin calculating determinant - also used to calculate U parameter
	Vec3Cross(pvec, dir, edge2);

	//If the determinant is near zero, ray lies in plane of triangle
	Vec3Dot(det, edge1, pvec);

	//If bCull is true
	if(bCull)
	{
		if(det < 0.00001f)
			return false ;

		//Calculate distance from vert0 to ray origin
		Vec3Sub(tvec, origin, v0);

		//Calculate U parameter and test bounds
		Vec3Dot(u, tvec, pvec);
		if(u < 0.0 || u > det)
			return false ;

		//Prepare to test v parameter
		Vec3Cross(qvec, tvec, edge1);

		//Calculate V parameter and test bounds
		Vec3Dot(v, dir, qvec);
		if(v < 0.0f || u + v > det)
			return false ;

		//Calculate t , scale paramter, ray intersect triangle
		Vec3Dot(*t, edge2, qvec);
		inv_det = 1.0f / det ;
		*t *= inv_det ;
		u *= inv_det ;
		v *= inv_det ;
	}
	else
	{
		if(det > -0.00001f && det < 0.00001)
			return false ;
		inv_det = 1.0f / det ;

		//calculate distance from v0 to ray origin
		Vec3Sub(tvec, origin, v0);

		//Calculate u parameter  and test bounds
		Vec3Dot(u, tvec, pvec);
		u *= inv_det ;
		if(u < 0.0 || u > 1.0)
			return false ;

		//prepare to test v parameter
		Vec3Cross(qvec, tvec, edge1);

		//Calculate v parameter and test bounds
		Vec3Dot(v, dir, qvec);
		v *= inv_det ;
		if(v < 0.0 || u + v > 1.0)
			return false ;

		//calculate t, ray intersect triangle
		Vec3Dot(*t, edge2, qvec);
		*t *= inv_det ;
	}

	return true ;
}// end for intersectWithTriangle</span>

Screenshot of demo sample program

This graph is the case when there is no crossover.

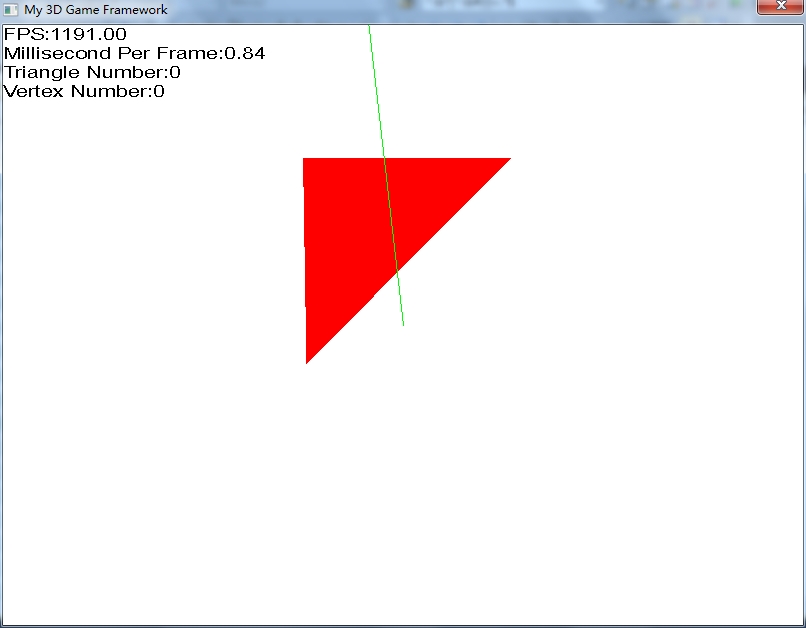
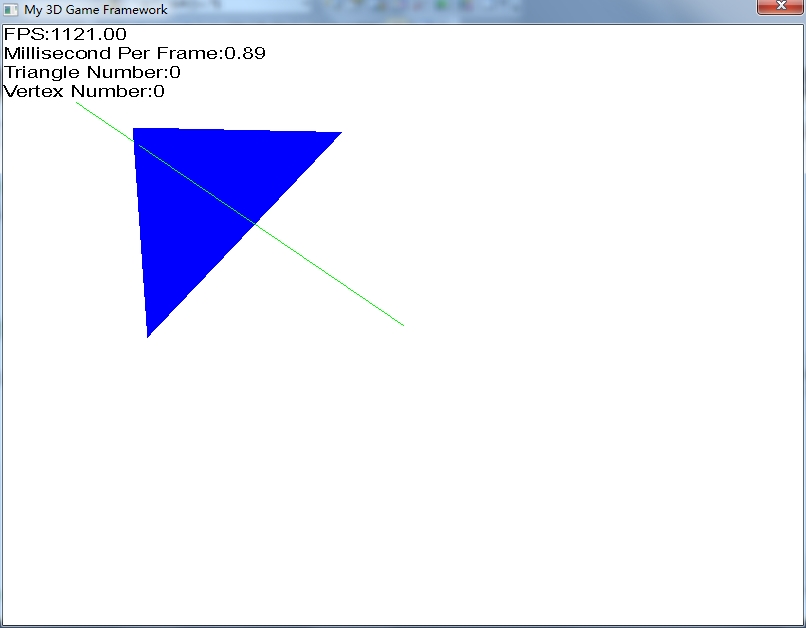
The following figure is a screenshot after the crossover:

Publisher: full stack programmer, stack length, please indicate the source for Reprint: https://javaforall.cn/116258.html Original link: https://javaforall.cn