Backpack Cryptograph is missing
Mathematics
Lattices
1. Vectors
Basic vector-to-scalar operations
Title:
v = (2,6,3), w = (1,0,0) and u = (7,7,2), calculate 3*(2*v - w) ∙ 2*u.
Calculate directly using sage
sage: v = vector([2,6,3]) sage: w = vector([1,0,0]) sage: u = vector([7,7,2]) sage: 3*(2*v-w)*2*u 702
flag is 702
2. Size and Basis
A set of vectors
v
1
,
v
2
.
.
.
v
k
∈
V
v_1,v_2...v_k\in V
v1, v2... vk < V is linear independent if and only if
a
1
v
1
+
a
2
v
2
+
.
.
.
+
a
k
v
k
=
0
a_1v_1+a_2v_2+...+a_kv_k=0
a1v1+a2v2+...+akvk=0
Only in
a
1
=
a
2
=
.
.
.
=
a
k
=
0
a_1=a_2=...=a_k=0
a1 =a2 =...= ak = 0 is true
The number of elements in a base is the dimension of the vector space
The size of a vector, defined as ||v||, is the product of itself and itself== ∣ ∣ v ∣ ∣ 2 = v ⋅ v ||v||^2=v\cdot v ∣∣v∣∣2=v⋅v==
A set of orthogonal bases v 1 , v 2 , . . . , v n ∈ V v_1,v_2,...,v_n\in V v1, v2,..., vn < V, the inner product of any two elements is 0== v i ⋅ v j = 0 , i ≠ j v_i\cdot v_j=0,i≠j vi⋅vj=0,i=j==
A set of orthonormal bases, which are i ∈ [ 1 , n ] i\in[1,n] i < [1,n] is satisfied== ∣ ∣ v i ∣ ∣ = 1 ||v_i||=1 Orthogonal Basis of vi =1==
Title:
Calculation v = ( 4 , 6 , 2 , 5 ) v=(4,6,2,5) v=(4,6,2,5) size
∣ ∣ v ∣ ∣ = v ⋅ v = ( 4 , 6 , 2 , 5 ) ⋅ ( 4 , 6 , 2 , 5 ) = 81 = 9 ||v||=\sqrt{v\cdot v}=\sqrt{(4,6,2,5)\cdot(4,6,2,5)}=\sqrt{81}=9 ∣∣v∣∣=v⋅v =(4,6,2,5)⋅(4,6,2,5) =81 =9
flag is 9
3. Gram Schmidt
Schmidt algorithm
You can group vectors v 1 , v 2 . . . v k ∈ V v_1,v_2...v_k\in V v1, v2... Orthogonalization of vk < V u 1 , u 2 , . . . , u k ∈ V u_1,u_2,...,u_k\in V u1,u2,...,uk∈V
u
1
=
v
1
u_1=v_1
u1=v1
Loop
i
=
2
,
3
,
.
.
.
,
n
i=2,3,...,n
i=2,3,...,n
Compute
μ
i
j
=
v
i
⋅
u
j
∣
∣
u
j
∣
∣
(
1
≤
j
<
i
)
\mu_{ij}=\frac{v_i·u_j}{||u_j||}(1\le j<i)
μij=∣∣uj∣∣vi⋅uj(1≤j<i)
Set u i = ∑ 1 ≤ j < i v i − μ i j ∗ u j u_i=\sum_{1\le j<i}v_i-\mu_{ij}*u_j ui=∑1≤j<ivi−μij∗uj
End Loop
Title:
v1 = (4,1,3,-1), v2 = (2,1,-3,4), v3 = (1,0,-2,7), v4 = (6, 2, 9, -5)
Calculating Standard Base Using Gram Schmidt Algorithm
Write half a day hand rubbing linear algebra, all bug s, not
Sent
The whole school line took over overnight.
Not even Schmidt could write
Sage has a built-in Gram Schmidt
sage: v0 = vector([4,1,3,-1]) sage: v1 = vector([2,1,-3,4]) sage: v2 = vector([1,0,-2,7]) sage: v3 = vector([6,2,9,-5]) sage: M = Matrix([v0,v1,v2,v3]) sage: M.gram_schmidt() ( [ 4 1 3 -1] [ 70/27 31/27 -23/9 104/27] [ -287/397 -405/397 799/397 844/397] [-1456/4023 273/298 1729/8046 455/4023], [ 1 0 0 0] [ -4/27 1 0 0] [ -1/3 468/397 1 0] [ 58/27 -659/794 439/4023 1] ) sage: M [ 4 1 3 -1] [ 2 1 -3 4] [ 1 0 -2 7] [ 6 2 9 -5]
flag is 0.91611 (rounded)
I also pasted another person's solution to implement the algorithm given by the title for learning reference
import numpy as np
v = [
np.array([4,1,3,-1]),
np.array([2,1,-3,4]),
np.array([1,0,-2,7]),
np.array([6,2,9,-5]),
]
"""
u1 = v1
Loop i = 2,3...,n
Compute μij = vi ∙ uj / ||uj||2, 1 ≤ j < i.
Set ui = vi - μij * uj (Sum over j for 1 ≤ j < i)
End Loop
"""
u = [v[0]]
for vi in v[1:]:
mi = [np.dot(vi, uj) / np.dot(uj, uj) for uj in u]
u += [vi - sum([mij * uj for (mij, uj) in zip(mi,u)])]
print(round(u[3][1], 5))
4. What's Lattice?
The basic space F of a lattice
Given a set of linearly independent vectors
v
1
,
v
2
,
.
.
.
,
v
n
∈
R
m
v_1,v_2,...,v_n\in R^m
v1, v2,..., vn < Rm, then the lattice generated by this set of vectors
L
L
L is made by
v
1
,
v
2
,
.
.
.
,
v
n
v_1,v_2,...,v_n
v1, v2,..., Combination of vn and corresponding integer coefficients
L
=
{
a
1
∗
v
1
+
a
2
∗
v
2
+
.
.
.
+
a
k
∗
v
k
:
a
1
,
a
2
,
.
.
.
,
a
n
∈
Z
}
L=\{a_1*v_1+a_2*v_2+...+a_k*v_k:a_1,a_2,...,a_n\in Z\}
L={a1∗v1+a2∗v2+...+ak∗vk:a1,a2,...,an∈Z}
The base of a lattice L can be any set of linearly independent vectors that generate L. Base selection is not unique
The choice of basis is far from unique
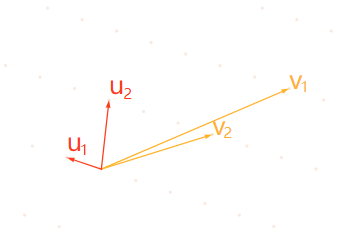
Any point can be reached by a set of base vectors and a number multiplied by them. A set of base vectors defines a basic domain
F
(
v
1
,
.
.
.
,
v
n
)
=
{
t
1
v
1
+
t
2
v
2
+
.
.
.
+
t
n
v
n
:
0
≤
t
i
<
1
}
F(v_1,...,v_n)=\{t_1v_1+t_2v_2+...+t_nv_n:0\le t_i<1\}
F(v1,...,vn)={t1v1+t2v2+...+tnvn:0≤ti<1}
For two-dimensional vectors, the basic space of the base vector is
v
1
⃗
\vec{v_1}
v1
And
u
1
⃗
\vec{u_1}
u1
Composed parallelogram
We can calculate the base space from the base vector. Title:
Title:
Known
v
1
=
(
6
,
2
,
−
3
)
,
v
2
=
(
5
,
1
,
4
)
,
v
3
=
(
2
,
7
,
1
)
v_1 = (6, 2, -3), v_2 = (5, 1, 4), v_3 = (2, 7, 1)
v1 = (6,2, 3),v2 = (5,1,4),v3 = (2,7,1), calculates the volume of the basic domain
V
o
l
(
F
)
=
∣
d
e
t
(
A
)
∣
=
∣
∣
6
2
−
3
5
1
4
2
7
1
∣
∣
Vol(F)=|det(A)|=\left|\left| \begin{matrix} 6 & 2 & -3\\ 5 & 1 & 4\\ 2 & 7 & 1 \end{matrix} \right|\right|
Vol(F)=∣det(A)∣=∣∣∣∣∣∣∣∣∣∣∣∣652217−341∣∣∣∣∣∣∣∣∣∣∣∣
Calculating with sage
sage: v = vector sage: v1 = v([6,2,-3]) sage: v2 = v([5,1,4]) sage: v3 = v([2,7,1]) sage: A = matrix([v1,v2,v3]) sage: A [ 6 2 -3] [ 5 1 4] [ 2 7 1] sage: det(A) -255
flag is 255
5. Gaussian Reduction
If you look closely, "lattice" begins to appear in every corner of cryptography. Sometimes they manipulate an encryption system, destroying unsafe parameters. The most famous example is Coppersmith's attack on RSA encryption.
Lattices can also be used to build encryption protocols based on two basic "hard" issues:
- The Shortest Vector Problem (SVP)
Given the base vector and the lattice, find the lattice L L The shortest non-zero vector of length in L. In other words, find a non-zero vector v ∈ L v\in L v < L causes ∣ ∣ v ∣ ∣ ||v|| Minimum v_
- The Closest Vector Problem (CVP)
Given a base vector, a lattice, and a target vector that is not on the lattice, find the closest lattice vector to the target vector.
Given an absence L L Vectors in L w ∈ R m w\in R^m w< Rm, find vector v ∈ L v\in L v < L causes ∣ ∣ v − w ∣ ∣ ||v-w|| _v_w_minimum
For general lattices, the SVP problem is very difficult, but for relatively simple cases, we have very effective algorithms to compute the solution or approximate solution of the problem. When the dimension of a lattice is less than or equal to 4, the deterministic solution can be calculated in polynomial time. For higher dimensions, only the approximate solution can be obtained.
Gauss invented an algorithm to find a two-dimensional lattice with a given base L L The best base for L. The output v1 of the algorithm is L L The shortest non-zero vector in L solves the two-dimensional SVP problem.
The Gauss algorithm achieves its goal roughly by subtracting a multiple of one base vector from another until it is no longer possible to make them smaller. This applies to two dimensions and is therefore a good visualization.

I am tired of translating one sentence to another. I don't want to tap any more formulas. Let's just draw a picture.
The script doesn't want to be written either
Direct interactive command line
import numpy as np ar = np.array v = ar([846835985, 9834798552],dtype='i8') u = ar([87502093, 123094980],dtype='i8') v1,v2 = u,v
>>> if siz2(v2) < siz2(v1):
print('swap')
v1,v2 = v2,v1
>>> m = int(v1.dot(v2)/v1.dot(v1));m
56
>>> v2 = v2 - m*v1;v2
array([-4053281223, 2941479672], dtype=int64)
>>> if siz2(v2) < siz2(v1):
print('swap')
v1,v2 = v2,v1
>>> m = int(v1.dot(v2)/v1.dot(v1));m
0
>>> v1
array([ 87502093, 123094980], dtype=int64)
>>> v2
array([-4053281223, 2941479672], dtype=int64)
>>> v1.dot(v2)
7410790865146821
flag is 7410790865146821
6. Find the Lattice
This kind of question is quite common in all kinds of competitions, you can refer to this one
https://xz.aliyun.com/t/7163
subject
from Crypto.Util.number import getPrime, inverse, bytes_to_long
import random
import math
FLAG = b'crypto{?????????????????????}'
def gen_key():
q = getPrime(512)
upper_bound = int(math.sqrt(q // 2))
lower_bound = int(math.sqrt(q // 4))
f = random.randint(2, upper_bound)
while True:
g = random.randint(lower_bound, upper_bound)
if math.gcd(f, g) == 1:
break
h = (inverse(f, q)*g) % q
return (q, h), (f, g)
def encrypt(q, h, m):
assert m < int(math.sqrt(q // 2))
r = random.randint(2, int(math.sqrt(q // 2)))
e = (r*h + m) % q
return e
def decrypt(q, h, f, g, e):
a = (f*e) % q
m = (a*inverse(f, g)) % g
return m
public, private = gen_key()
q, h = public
f, g = private
m = bytes_to_long(FLAG)
e = encrypt(q, h, m)
print(f'Public key: {(q,h)}')
print(f'Encrypted Flag: {e}')
Known values are
q,h,e
among
h
≡
f
−
1
g
m
o
d
p
e
≡
(
r
h
+
m
)
m
o
d
p
h\equiv f^{-1}g\mod p\\ e\equiv (rh+m)\mod p
h≡f−1gmodpe≡(rh+m)modp
q 512 bits
f,g less than 256 bits
h, e 512 bits
r 256 bits
m is flag, about 231 bit in size
m, decrypt parameters, f and g are unknown
The only relationship we know about f and g is
f
⋅
h
≡
g
m
o
d
p
f\cdot h\equiv g\mod p
f⋅h≡gmodp
You need to use the lattice idea of the previous question here
We can construct a lattice composed of two row vectors (1,h),(0,q) in the matrix M below:
M
=
[
1
h
0
q
]
M= \left[ \begin{matrix} 1&h\\ 0&q \end{matrix} \right]
M=[10hq]
First, the vector (f,g) is on this lattice, that is, the coefficients of existence
a
a
a,
b
b
b Make
a
(
1
,
h
)
+
b
(
0
,
q
)
=
(
f
,
p
)
a(1,h)+b(0,q)=(f,p)
a(1,h)+b(0,q)=(f,p)
f
⋅
h
≡
g
m
o
d
q
f
⋅
h
=
g
+
u
⋅
q
f
⋅
h
−
u
⋅
q
=
g
f\cdot h\equiv g\mod q\\ f·h=g+u·q\\ f·h-u·q=g\\
f⋅h≡gmodqf⋅h=g+u⋅qf⋅h−u⋅q=g
That is
a
,
b
=
f
,
−
u
a,b=f,-u
a,b=f, u satisfies the condition
Vectors (f,g) can be represented by a linear combination of integer coefficients (f, -u) of two sets of base vectors M, so the vector (f,g) is on this lattice.
For two base vectors,
(1, h): 512 bits
(0, q): 512 bits
And the length of the variable (f,g): about 256 bits
It is very small compared to the base vector.
It is very likely that this (f, g) is the shortest vector of this lattice (Gaussian heurstic).
I didn't write a program for the last question, so I'll make it up now...
# sage
# GaussLatticeReduction
def Gauss(v1, v2):
while True:
if v2.norm() < v1.norm():
v1, v2 = v2, v1
m = round( v1*v2 / v1.norm()^2 )
if m == 0:
return (v1, v2)
v2 = v2 - m*v1
sage: v = vector([1,h]) sage: u = vector([0,q]) sage: Gauss(u,v) ((47251817614431369468151088301948722761694622606220578981561236563325808178756, 43997957885147078115851147456370880089696256470389782348293341937915504254589), (-67269010250212717075432182693043963184097648880165008621907831284647116025901, 99012763459529858809608436133564630524350106000242070336818304053467942269178))
The first vector of the output is (f,g)
>>> len(bin(f)[2:]) 255 >>> len(bin(g)[2:]) 255
Length is also satisfied
Now run the decrypt function directly to get flag
q, h = (7638232120454925879231554234011842347641017888219021175304217358715878636183252433454896490677496516149889316745664606749499241420160898019203925115292257, 2163268902194560093843693572170199707501787797497998463462129592239973581462651622978282637513865274199374452805292639586264791317439029535926401109074800) e = 5605696495253720664142881956908624307570671858477482119657436163663663844731169035682344974286379049123733356009125671924280312532755241162267269123486523 f,g = 47251817614431369468151088301948722761694622606220578981561236563325808178756, 43997957885147078115851147456370880089696256470389782348293341937915504254589 print(l2b(decrypt(q,h,f,g,e)))
crypto{}
7. Backpack Cryptography
Backpack encryption algorithm
I didn't come up with the question
Reference resources Cryptography - Backpack algorithm for public key cryptography 1_ Sweeping through the vicissitudes - CSDN Blog
This is an early public key algorithm. The security of the backpack algorithm originates from the backpack problem. He is a NP-complete problem, but later found that the algorithm is not secure, but because it proves how to use the NP-complete problem in public key cryptography
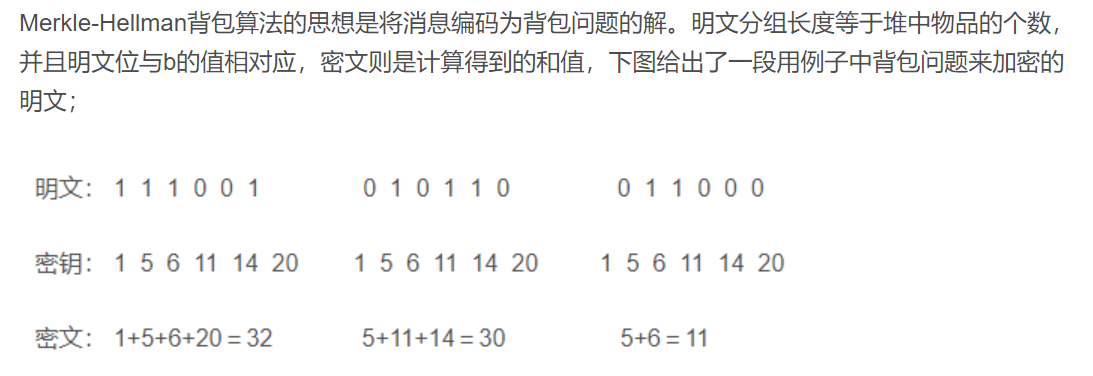
For the easy-to-solve knapsack problem, the hyper-incremental sequence can be chosen, and the corresponding knapsack problem can be easily solved.
Hyper-incremental sequence: Each of its items is greater than the sum of all its previous items, for example, {1, 3, 6, 13, 27, 52} is a super-incremental sequence, while {1, 3, 4, 9, 15, 25} is not.
Backpacks of non-super-incremental sequences are difficult problems, they do not have fast algorithms.
The backpack encryption algorithm is that the public key is a non-super-incremental sequence backpack, and the private key is a super-incremental sequence and converts the two to each other r r r
The basic idea of deciphering is that you don't have to find the correct module q q q and multiplier r r r (trapdoor information) just need to find any module k ′ k' k'and multiplier t ′ t' t', then use k ′ k' k'and t ′ t' t'to public backpack vectors b b b Find a new super-increment vector.
The script I'm using comes from here: Backpack Encryption - CTF Wiki (ctf-wiki.org) Using scripts on wiki es
import binascii
# open the public key and strip the spaces so we have a decent array
pubKey = a
nbit = len(pubKey)
# open the encoded message
encoded = c
print("start")
# create a large matrix of 0's (dimensions are public key length +1)
A = Matrix(ZZ, nbit + 1, nbit + 1)
# fill in the identity matrix
for i in range(nbit):
A[i, i] = 1
# replace the bottom row with your public key
for i in range(nbit):
A[i, nbit] = pubKey[i]
# last element is the encoded message
A[nbit, nbit] = -int(encoded)
res = A.LLL()
for i in range(0, nbit + 1):
# print solution
M = res.row(i).list()
flag = True
for m in M:
if m != 0 and m != 1:
flag = False
break
if flag:
print(i, M)
M = ''.join(str(j) for j in M)
# remove the last bit
M = M[:-1]
M = hex(int(M, 2))[2:-1]
print(M)
But no results