Assignment #3
A primer on named entity recognition
In this section, we will build several different models to implement named entity recognition (NER). NER is a sub-task of information extraction, which aims to locate and classify named entities in text into predefined categories, such as names, organizations, locations, time expressions, quantities, currency values, percentages, etc. For a given word in the context, it is predicted whether it represents one of the following four categories:
- Personal Name (PER): For example, "Martha Stewart", "Obama", "Tim Wagner" and so on, pronouns "he" or "she" are not considered as named entities.
- ORG: For example, "American Airlines", "Goldman Sachs", "Department of Defense".
- Location (LOC): For example, "Germany", "Panama Strait", "Brussels", excluding unnamed locations such as "the bar" or "the farm".
- Other (MISC): such as "Japanese", "USD", "1000", "Englishmen".
We define this as a five-category problem, using the above four classes and an empty class (O) to represent words that do not represent named entities (most words belong to this category). For entities spanning more than one word ("Department of Defense"), each word is marked separately, and each successive sequence of non-empty tags is treated as an entity.
Here is an example sentence(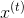
Each word is marked with a named entity(
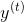) and hypothesis prediction generated by the system(
):
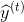In the above example, the system mistakenly predicts that "American" is a MISC class, and ignores "Airlines" and "Corp". Overall, it predicts three entities, "American", "AMR", "Tim Wagner". In order to evaluate the quality of NER system output, we focus on accuracy, recall rate and F1 value. In particular, we report accuracy, recall and F1 values at both token and named entity levels. In the previous example:
-
Accuracy is calculated as the ratio of the correct non-empty labels predicted to the total number of non-empty labels predicted (p=3/4 in the example above).
-
The recall rate is calculated as the ratio of the predicted total number of correct non-empty labels to the correct total number of non-empty labels (r=3/6 in the example above).
-
F1 is the harmonic average of accuracy and recall (in the example above, F1=6/10).
For entity level F1:
- The accuracy rate is the score of predicting the span of entity names, which is completely consistent with the span in the gold standard evaluation data. In our example, "AMR" will be mismarked because it does not include the entity as a whole, that is, "AMR Corp.", and "American" will also get a 1/3 accuracy score.
- The recall rate is also the number of names in the gold standard that appear at exactly the same location in the forecast. Here, we get a recall score of 1/3.
- Finally, the F1 value is still the harmonic average of the two, with 1/3 in the example.
Our model also outputs a word-level obfuscation matrix. Obfuscation matrix is a specific table layout that allows visual classification performance. Each column of the matrix represents an instance in the predicted category, and each row represents an instance in the actual category. The name derives from the fact that it can easily see whether the system confuses two classes (i.e., one class is usually mismarked as another).
1.A window into NER
Let's look at a simple baseline model that uses features from surrounding windows to predict the labels of each word separately.
Figure 1 shows an example of an input sequence and the first window of the sequence. order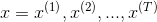
For an input sequence of length T,
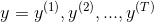It is an output sequence of length T. Each element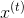and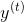They are one-hot vectors representing the words indexed to t in the sequence. In a window-based classifier, each input sequence is divided into T new data points, each point represents a window and its label. By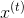The w words on the left and right sides are joined together.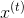The surrounding window constructs a new input:
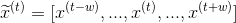We continue to use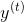As its label. For the tag-centered window at the beginning of the sentence, we add a special start tag (< start >) at the beginning of the window, and for the tag-centered window at the end of the sentence, we add a special end tag (< end >). For example, consider building a window around "Jim" in the sentence above. If the window size is 1, we add a start word to the window (producing a window with [<START>, Jim, buy]). If the window size is 2, we add two start words to the window (producing a window with [<START>, <START>, Jim, buy, 300]).
With these, each input and output has a uniform length (w and 1, respectively), and we can use a simple feedforward neural network from the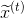
Forecast:
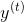As a simple but effective model for predicting labels from each window, we will use a single hidden layer with ReLU activation, combined with the soft max output layer, and cross-entropy loss:
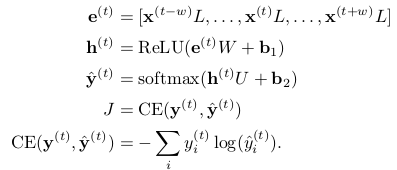
among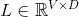
It's a word vector.
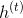It's H-dimensional.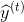It is C-dimensional, where V is the size of the vocabulary, D is the size of the word vector, H is the size of the hidden layer, and C is the number of predicted categories (5 here).
(a)
i. Provide two examples of sentences containing named entities with ambiguous types (e.g., entities can be individuals or organizations, or organizations or non-entities).
1)"Spokesperson for Levis, Bill Murray, said...", where Levis may be a person's name or an organization.
2) Heartbreak is a new virus, in which Heartbreak may be another named entity (actually the name of virus) or simply a noun.
ii. Why is it important to use features other than words themselves to predict named entity labels?
Normally named entities are rare words, such as person names or "heartbreak", and the use of such features as case makes the system generalized.
iii. Describe at least two features that help to predict whether a word belongs to a named entity (excluding words).
Word capitalization and part of speech.
(b)
i. If the window size is w, then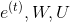
What is the dimension?
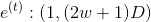
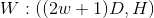
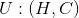
ii. What is the computational complexity of tags whose predicted sequence length is T?
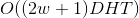
(c) Implementing a window-based classifier model:
i. In make_windowed_data function, batch of an input sequence is converted to batch of a windowed input-output pair.
def make_windowed_data(data, start, end, window_size = 1):
"""Uses the input sequences in @data to construct new windowed data points.
TODO: In the code below, construct a window from each word in the
input sentence by concatenating the words @window_size to the left
and @window_size to the right to the word. Finally, add this new
window data point and its label. to windowed_data.
Args:
data: is a list of (sentence, labels) tuples. @sentence is a list
containing the words in the sentence and @label is a list of
output labels. Each word is itself a list of
@n_features features. For example, the sentence "Chris
Manning is amazing" and labels "PER PER O O" would become
([[1,9], [2,9], [3,8], [4,8]], [1, 1, 4, 4]). Here "Chris"
the word has been featurized as "[1, 9]", and "[1, 1, 4, 4]"
is the list of labels.
start: the featurized `start' token to be used for windows at the very
beginning of the sentence.
end: the featurized `end' token to be used for windows at the very
end of the sentence.
window_size: the length of the window to construct.
Returns:
a new list of data points, corresponding to each window in the
sentence. Each data point consists of a list of
@n_window_features features (corresponding to words from the
window) to be used in the sentence and its NER label.
If start=[5,8] and end=[6,8], the above example should return
the list
[([5, 8, 1, 9, 2, 9], 1),
([1, 9, 2, 9, 3, 8], 1),
...
]
"""
windowed_data = []
for sentence, labels in data:
# YOUR CODE HERE (5-20 lines)
T = len(labels) # Sequence Length T
for t in range(T): # Traversing through each word in a single sequence
sen2fea = []
for l in range(window_size, 0, -1): # w Words in the Left Window
if t-l < 0:
sen2fea.extend(start)
else:
sen2fea.extend(sentence[t-l])
sen2fea.extend(sentence[t])
for r in range(1, window_size+1): # w words in the right window
if t+r >= T:
sen2fea.extend(end)
else:
sen2fea.extend(sentence[t+r])
windowed_data.append((sen2fea, labels[t]))
# END YOUR CODE
return windowed_dataii. Implement the feed-forward model described above in the Windows Model class.
class WindowModel(NERModel):
"""
Implements a feedforward neural network with an embedding layer and
single hidden layer.
This network will predict what label (e.g. PER) should be given to a
given token (e.g. Manning) by using a featurized window around the token.
"""
def add_placeholders(self):
"""Generates placeholder variables to represent the input tensors
These placeholders are used as inputs by the rest of the model building and will be fed
data during training. Note that when "None" is in a placeholder's shape, it's flexible
(so we can use different batch sizes without rebuilding the model).
Adds following nodes to the computational graph
input_placeholder: Input placeholder tensor of shape (None, n_window_features), type tf.int32
labels_placeholder: Labels placeholder tensor of shape (None,), type tf.int32
dropout_placeholder: Dropout value placeholder (scalar), type tf.float32
Add these placeholders to self as the instance variables
self.input_placeholder
self.labels_placeholder
self.dropout_placeholder
(Don't change the variable names)
"""
# YOUR CODE HERE (~3-5 lines)
self.input_placeholder = tf.placeholder(shape=[None, Config.n_window_features], dtype=tf.int32)
self.labels_placeholder = tf.placeholder(shape=[None, ], dtype=tf.int32)
self.dropout_placeholder = tf.placeholder(dtype=tf.float32)
# END YOUR CODE
def create_feed_dict(self, inputs_batch, labels_batch=None, dropout=1):
"""Creates the feed_dict for the model.
A feed_dict takes the form of:
feed_dict = {
<placeholder>: <tensor of values to be passed for placeholder>,
....
}
Hint: The keys for the feed_dict should be a subset of the placeholder
tensors created in add_placeholders.
Hint: When an argument is None, don't add it to the feed_dict.
Args:
inputs_batch: A batch of input data.
labels_batch: A batch of label data.
dropout: The dropout rate.
Returns:
feed_dict: The feed dictionary mapping from placeholders to values.
"""
# YOUR CODE HERE (~5-10 lines)
if labels_batch is None:
feed_dict = {self.input_placeholder: inputs_batch,
self.dropout_placeholder: dropout}
else:
feed_dict = {self.input_placeholder: inputs_batch,
self.labels_placeholder: labels_batch,
self.dropout_placeholder: dropout}
# END YOUR CODE
return feed_dict
def add_embedding(self):
"""Adds an embedding layer that maps from input tokens (integers) to vectors and then
concatenates those vectors:
- Creates an embedding tensor and initializes it with self.pretrained_embeddings.
- Uses the input_placeholder to index into the embeddings tensor, resulting in a
tensor of shape (None, n_window_features, embedding_size).
- Concatenates the embeddings by reshaping the embeddings tensor to shape
(None, n_window_features * embedding_size).
Hint: You might find tf.nn.embedding_lookup useful.
Hint: You can use tf.reshape to concatenate the vectors. See following link to understand
what -1 in a shape means.
https://www.tensorflow.org/api_docs/python/array_ops/shapes_and_shaping#reshape.
Returns:
embeddings: tf.Tensor of shape (None, n_window_features*embed_size)
"""
# YOUR CODE HERE (!3-5 lines)
embedding = tf.Variable(self.pretrained_embeddings, name='embedding')
embeddings_3d = tf.nn.embedding_lookup(embedding, self.input_placeholder)
embeddings = tf.reshape(embeddings_3d, shape=[-1, Config.n_window_features*Config.embed_size])
# END YOUR CODE
return embeddings
def add_prediction_op(self):
"""Adds the 1-hidden-layer NN:
h = Relu(xW + b1)
h_drop = Dropout(h, dropout_rate)
pred = h_dropU + b2
Recall that we are not applying a softmax to pred. The softmax will instead be done in
the add_loss_op function, which improves efficiency because we can use
tf.nn.softmax_cross_entropy_with_logits
When creating a new variable, use the tf.get_variable function
because it lets us specify an initializer.
Use tf.contrib.layers.xavier_initializer to initialize matrices.
This is TensorFlow's implementation of the Xavier initialization
trick we used in last assignment.
Note: tf.nn.dropout takes the keep probability (1 - p_drop) as an argument.
The keep probability should be set to the value of dropout_rate.
Returns:
pred: tf.Tensor of shape (batch_size, n_classes)
"""
x = self.add_embedding()
dropout_rate = self.dropout_placeholder
# YOUR CODE HERE (~10-20 lines)
W = tf.get_variable(initializer=tf.contrib.layers.xavier_initializer(),
shape=[Config.n_window_features*Config.embed_size, Config.hidden_size],
name='W')
b1 = tf.get_variable(initializer=tf.zeros(Config.hidden_size), name='b1')
h = tf.nn.relu(tf.matmul(x, W) + b1)
h_drop = tf.nn.dropout(h, keep_prob=dropout_rate)
U = tf.get_variable(initializer=tf.contrib.layers.xavier_initializer(),
shape=[Config.hidden_size, Config.n_classes],
name='U')
b2 = tf.get_variable(initializer=tf.zeros(Config.n_classes), name='b2')
pred = tf.matmul(h_drop, U) + b2
# END YOUR CODE
return pred
def add_loss_op(self, pred):
"""Adds Ops for the loss function to the computational graph.
In this case we are using cross entropy loss.
The loss should be averaged over all examples in the current minibatch.
Remember that you can use tf.nn.sparse_softmax_cross_entropy_with_logits to simplify your
implementation. You might find tf.reduce_mean useful.
Args:
pred: A tensor of shape (batch_size, n_classes) containing the output of the neural
network before the softmax layer.
Returns:
loss: A 0-d tensor (scalar)
"""
# YOUR CODE HERE (~2-5 lines)
loss = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(logits=pred,
labels=self.labels_placeholder))
# END YOUR CODE
return loss
def add_training_op(self, loss):
"""Sets up the training Ops.
Creates an optimizer and applies the gradients to all trainable variables.
The Op returned by this function is what must be passed to the
`sess.run()` call to cause the model to train. See
https://www.tensorflow.org/versions/r0.7/api_docs/python/train.html#Optimizer
for more information.
Use tf.train.AdamOptimizer for this model.
Calling optimizer.minimize() will return a train_op object.
Args:
loss: Loss tensor, from cross_entropy_loss.
Returns:
train_op: The Op for training.
"""
# YOUR CODE HERE (~1-2 lines)
train_op = tf.train.AdamOptimizer(learning_rate=Config.lr).minimize(loss)
# END YOUR CODE
return train_op
def preprocess_sequence_data(self, examples):
return make_windowed_data(examples, start=self.helper.START, end=self.helper.END, window_size=self.config.window_size)
def consolidate_predictions(self, examples_raw, examples, preds):
"""Batch the predictions into groups of sentence length.
"""
ret = []
#pdb.set_trace()
i = 0
for sentence, labels in examples_raw:
labels_ = preds[i:i+len(sentence)]
i += len(sentence)
ret.append([sentence, labels, labels_])
return ret
def predict_on_batch(self, sess, inputs_batch):
"""Make predictions for the provided batch of data
Args:
sess: tf.Session()
input_batch: np.ndarray of shape (n_samples, n_features)
Returns:
predictions: np.ndarray of shape (n_samples, n_classes)
"""
feed = self.create_feed_dict(inputs_batch)
predictions = sess.run(tf.argmax(self.pred, axis=1), feed_dict=feed)
return predictions
def train_on_batch(self, sess, inputs_batch, labels_batch):
feed = self.create_feed_dict(inputs_batch, labels_batch=labels_batch,
dropout=self.config.dropout)
_, loss = sess.run([self.train_op, self.loss], feed_dict=feed)
return loss
def __init__(self, helper, config, pretrained_embeddings, report=None):
super(WindowModel, self).__init__(helper, config, report)
self.pretrained_embeddings = pretrained_embeddings
# Defining placeholders.
self.input_placeholder = None
self.labels_placeholder = None
self.dropout_placeholder = None
self.build()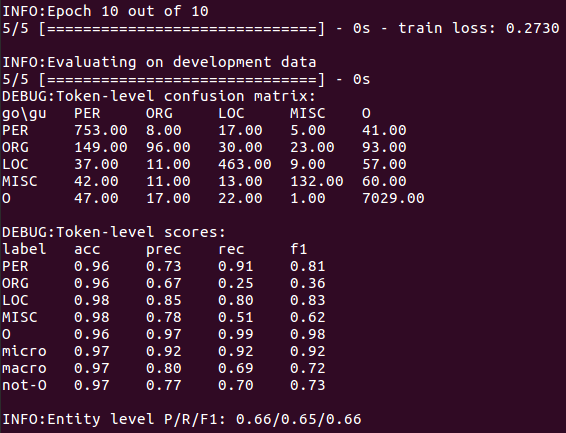
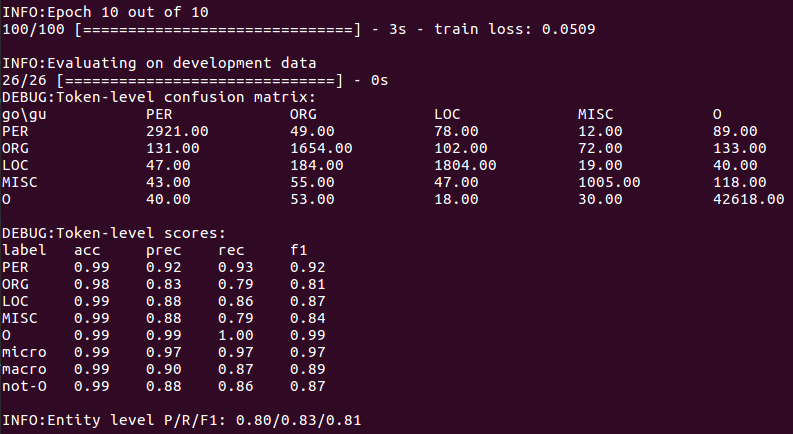
iii. Training models, models and outputs will be stored in results/window/<timestamp>/results.txt contains the formatted output of the model's prediction on the verification set, and log files contain the printed output, i.e., the confusion matrix and F1 value calculated in training.
(d) Prediction using the file analysis model generated above.
i. Briefly describe the information about model prediction errors displayed by the obfuscation matrix.
The confusion matrix shows that the biggest source of confusion in the model comes from organization labels, many of which are mistaken for names or ignored directly. On the other hand, names seem to be well recognized.
ii. Describe at least two modeling constraints for window-based models.
The window-based model can not use the information from adjacent prediction to eliminate ambiguity in label decision-making, which leads to discontinuous entity prediction.
On the difference between tf.Variable and tf.get_variable:
https://blog.csdn.net/MrR1ght/article/details/81228087
On tf.nn.embedding_lookup:
https://blog.csdn.net/yinruiyang94/article/details/77600453
https://tensorflow.google.cn/api_docs/python/tf/nn/embedding_lookup
On tf.contrib.layers.xavier_initializer:
https://blog.csdn.net/yinruiyang94/article/details/78354257
https://tensorflow.google.cn/api_docs/python/tf/contrib/layers/xavier_initializer