Alice and Bob are playing jigsaw.
The rules of Jingzi chess game are simple: two people take turns to put pieces on the 3 * 3 board, Alice puts "X", Bob puts "O", and Alice holds the lead. When the same piece occupies three squares of a row, a column or a diagonal, the game ends and the holder of the piece wins. When the board is filled, the game is over and the two sides are tied.
Alice designed a way to score the game:
- for situations where Alice has won, the evaluation score is (number of empty squares on the chessboard + 1);
- for the situation that Bob has won, the evaluation score is - (number of empty squares on the chessboard + 1);
- for a draw, the assessment score is 0;


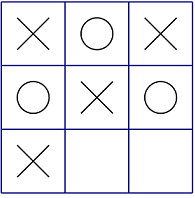
For example, in the situation above, Alice has won, and there are two spaces on the chessboard, so the score of the situation is 2 + 1 = 3.
Since Alice doesn't like computing, he asks you who are good at programming. If both players play chess with the best strategy, what is the final score of the current situation?

The first set of data:
Alice put the chess piece in the lower left corner (or the lower right corner) to reach the situation in the problem description, scoring 3.
3 is the maximum score in the situation that Alice can reach after playing chess.
The second set of data:


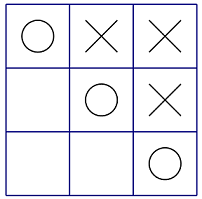
Bob has won (as shown in the figure), and the score of this situation is - (3 + 1) = - 4.
The third group of data:
If both sides adopt the best strategy, the game is tied and the final score is 0.

 

 

#include<iostream>
using namespace std;
int lef (int a[]){//¼ÆËãÆåÅÌÉÏ»¹ÓжàÉÙ¿Õ°×λ 
    int i=0,flag=0;
    for(;i<9;i++){
        if(a[i]==0){
            flag++;
        }
    }
    return flag;
}
int show(int a[]){//´òÓ¡Æå¾Ö 
               for(int i=0;i<9;i++){
                    cout<<a[i]<<" ";
                }
                cout<<endl;
                return 0;
}
int win1(int a[]){//ÅжÏʤ¸º£¬Èç¹ûûÓÐÃ÷È·½á¹û·µ»Ø0 
    if((a[1]*a[2]*a[0]==1) ||
       (a[3]*a[4]*a[5]==1) ||
       (a[6]*a[7]*a[8]==1) ||
       (a[0]*a[3]*a[3]*a[6]*a[6]==1) ||
       (a[1]*a[4]*a[4]*a[7]*a[7]==1) ||
       (a[2]*a[8]*a[5]==1) ||
       (a[0]*a[4]*a[8]==1) ||
       (a[2]*a[6]*a[4]==1) ){
        return 1;
    }else if((a[1]*a[2]*a[0]==8) ||
       (a[3]*a[4]*a[5]==8) ||
       (a[6]*a[7]*a[8]==8) ||
       (a[0]*a[3]*a[6]==8) ||
       (a[1]*a[4]*a[7]==8) ||
       (a[2]*a[8]*a[5]==8) ||
       (a[0]*a[4]*a[8]==8) ||
       (a[2]*a[6]*a[4]==8) ){
        return 2;
       }else return 0;
}
int com(int a[],int b){
    if(win1(a)==1){
        return lef(a)+1;
    }else if (win1(a)==2) {
        return -lef(a)-1;}
    if(lef(a)==0){
        return 0;
    }
    int k,j,c[9],d[9],mmm=-1000;//ÓÃÊý×écÀ´±£´æµ±Ç°¾ÖÃæÒԱ㸴ԭ£¬Êý×éd±£´æµÃ·ÖÇé¿ö 
    for(k=0;k<9;k++){
        c[k]=a[k];
        d[k]=0;
    }
    if(b==1){
        for(j=0;j<9;j++){
            if(c[j]==0){
                c[j]=1;
                d[j]=com(c,2);
                c[j]=0;
            }
        }
        for(k=0;k<9;k++){
            if(d[k]>=mmm && c[k]==0){
                mmm=d[k];
            }
        }
        return mmm;
    }else if (b==2){
        mmm=1000;
        for(j=0;j<9;j++){
            if(c[j]==0){
                c[j]=2;
                d[j]=com(c,1);
                c[j]=0;
            }
        }
        for(k=0;k<9;k++){
            if(d[k]<=mmm && c[k]==0){
                mmm=d[k];

            }
        }
        return mmm;
    }
    return 0;
}
int main(){
    int i,k,l,t;
    cin>>t;
    int data[9],result[100];
    for (i=0;i<t;i++){
            for(k=0;k<9;k++){
        cin>>data[k];
    }
    result[i]=com(data,1);
    }
    for(i=0;i<t;i++){
        cout<<result[i]<<endl;
    }
    return 0;
}