D * algorithm (Dynamic A Star)
Symbol and function description
Openlist is a tool that can be used to do Breadth first search Queue of
The identification tag s of node state are divided into three categories: those that have not joined the open table (new), those in the open table (open), and those that have been in the open table but have been removed (closed).
The cost from each node to the end point G is h, the cost between two nodes (state) is C (X,Y), and the cost from X to the end point h is the cost from the previous node (parent node) Y to the end point + the cost between X and Y
The minimum H value of each node is k, which represents the minimum cost from the point to point G in the whole graph environment. In the process of calculation and update, k=h for the point marked new, k = min {K, newh} for the point marked open, and K = min {K, newh} for the point marked closed.
The main functions of the algorithm are process state and modify cost. The former is used to calculate the optimal path to target G, and the latter is used to change the overhead C (X,Y) between two nodes (States) and place the affected nodes (States) in Openlist.
First search
Place the end point in the Openlist and search with Dijkstra until the search reaches the starting point and ends. After the search, each searched node is identified as closed, k=h of each node, and its parent node is the one with the lowest K value in the neighborhood.
When the search is over, you can search all the way to the destination by finding the parent node from the starting point. If the Openlist is not empty at the end of the search, the value of node h in it must not be smaller than that of the starting point.
Encounter obstacles
If the next point (parent node) of the current point is an obstacle, modify its h value and put it into the Openlist (if it is a wall, modify it to the h value of the wall, such as infinity), but its K value remains unchanged, that is, k = k = min {K, newh}, so the point will be taken out preferentially and spread.
The diffusion process needs to use the pseudo code process state in the paper until k_ min>= state_ h . That is, if the calculated H value does not need to be smaller than the last k value when diffusing to a node, the external diffusion can be ended at that point.
Pseudo code and comments
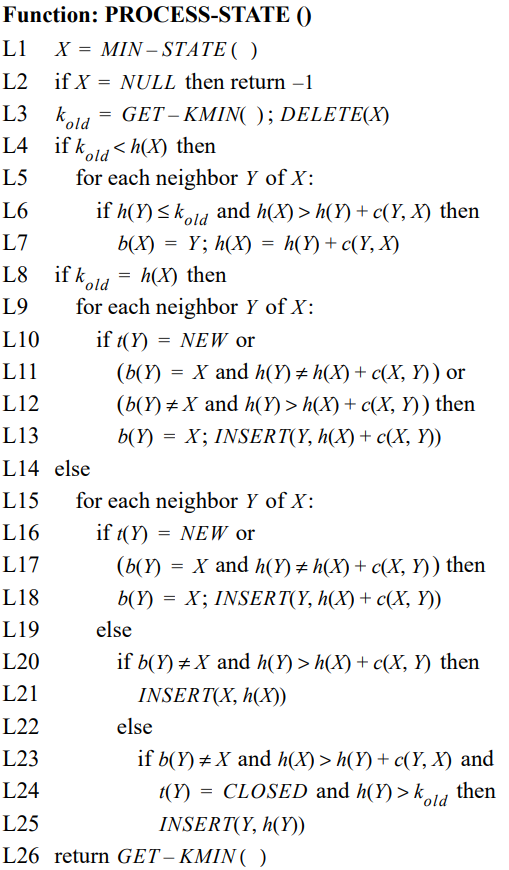
Function : Process-State() ---------- Node processing function L1: X=Min-State()----- From all nodes k Minimum value L2: if X=Null then return -1----- Openlist Empty, end L3: K_old=Get-Kmin();Delete(X)----- Get this point k Value and pop up the point Openlist queue L4: if K_old<h(x) then----- Compare this point h Value and K Value( h Value rising state) L5: - for each neighbor Y of X:----- Traversing neighborhood nodes Y L6: -- if h(Y)<= K_old and h(x)>h(y)+c(x,y)----- Y Is not on the rise and is updated with it x After, h of h Smaller value L7: --- b(x)= Y; h(x)=h(y)+c(x,y)---- to update x Parent node and its h value L8: if K_old=h(x) then----- Compare this point h Value and K Value( h Value unchanged (status) L9: - for each neighbor Y of X:----- Traversing neighborhood nodes Y L10: -- if t(Y)= New or----- Y Is first added to Openlist And deal with L11: --—(b(Y)= X and h(Y)!=h(x)+c(x,y))or----- Y yes X The child node of, and its h The value does not need to be changed L12: --—(b(Y)!= X and h(Y)>h(x)+c(x,y))or----- Y no X The child node of, and its h The value can become smaller L13: --- b(Y)= X; insert(Y,h(x)+c(x,y))----- take X As Y Parent node of, modify its h Value and set Y Add points to Openlist in L14: else ----- Compare this point h Value and K Value( h Value (falling state) L15: - for each neighbor Y of X:----- Traversing neighborhood nodes Y L16: -- if t(Y)= New or----- Y Is first added to Openlist And deal with L17: --—(b(Y)= X and h(Y)!=h(x)+c(x,y))or----- Y yes X The child node of, and its h The value does not need to be changed L18: --- b(Y)= X; insert(Y,h(x)+c(x,y))----- take X As Y Parent node of, modify its h Value and set Y Add points to Openlist in L19: -- else L20: --— if((b(Y)!= X and h(Y)>h(x)+c(x,y))then----- Y no X The child node of, and its h The value can become smaller L21: --- insert(X,h(x))----- modify X of h Value and add its point to Openlist in L22: --— else L23: --- if((b(Y)!= X and h(Y)>h(x)+c(x,y) and----- Y no X The child node of, and its h The value can become smaller L24: ---— t(Y)= Closed and h(Y)>K_old then ----Y be not in Openlist Medium, and h The value is rising L25: ---— insert(Y,h(Y))----modify Y of h Value and add its point to Openlist in L25: return Get-Kmin() ----Return to this point k value

Function : Modify-cost(x,y,cval) ---------- Distance processing function between two nodes L1: c(X,X)=cval ----- Reset the distance between two nodes L2: if t(X)=Closed then insert(X,h(x))----- X be not in Openlist If in, modify its h Value and add to Openlist L3: return Get-Kmin() ----return X spot k value
Program understanding
Process state(): used to calculate the optimal path to target G.
Get the node with the lowest k value from the open table and remove it.
Classify the point, traverse its neighborhood, and see whether the parent node and h value need to be modified and added to the open table. The classification is generally as follows:
First, conduct a k-test_ Old < h (x) judge whether the h value of X needs to be adjusted:
k_ Old < h (x): it indicates that the node is affected by obstacles and X is in raise state. It can be assumed that when x suddenly changes into a wall, the h value increases, or its parent node is affected by the node that suddenly changes into a wall, resulting in the increase of h value, which finally affects him.
Then traverse its neighborhood, if the h value of y point does not rise, and the h value of x can become smaller through this point.
In the above case, change the parent node of x to y and reset the value of h.
Then judge again to see whether the h value of y needs to be adjusted:
k_old=h(x): in the first traversal stage, or the node x is not affected by obstacles.
Then traverse its neighborhood, and the judgment after if represents: y is traversed for the first time; Or the parent node of Y is X, but the values of h(y) and h(x)+c(x,y) are different, because k_old=h(x), which means that h(y) has been changed, but h(x) has not changed; Or Y's parent node is not X, but if X becomes its parent node, it will have a smaller h(y) value.
In the above three cases, adjust the h value of Y according to the h value of X, take x as the parent node of Y, and add y to the open table
k_old!= h(x): indicates that the node is affected and traverses its neighborhood.
If y is the point traversed for the first time; Or X is the parent node of Y, but the values of h(y) and h(x)+c(x,y) are different, which indicates that h(x) has been changed, but h(y) has not changed;
In the above case, adjust the h value of Y according to the h value of X, take x as the parent node of Y, and add y to the open table.
If the parent node of Y is not X, but making X its parent node will have a smaller h(y) value.
In the above case, adjust the h value of X and add x to the open table.
If the parent node of Y is not x, but let y become the parent node of X, x will have a smaller h(x) value, and y has been removed by the open table, and the h(y) value is rising (that is, y is affected).
In the above case, adjust the h value of Y and add y to the open table.
Summary
Adjust the h value of x and its parent node:
1,k_old<h(x) &&h(y)<= K_old and h(x)>h(y)+c(x,y)
The h value of X is not adjusted, but x is added to the open table:
1,k_old!=h(x) &&((b(Y)!= X and h(Y)>h(x)+c(x,y))
Adjust the h value of Y and its parent node, and add y to the open table:
1,k_old=h(x) && t(Y)= "new" 2,k_old=h(x) &&(b(Y)= X and h(Y)!=h(x)+c(x,y)) 3,k_old=h(x) &&((b(Y)!= X and h(Y)>h(x)+c(x,y)) 4,k_old!=h(x) &&t(Y)= New 5,k_old!=h(x) &&(b(Y)= X and h(Y)!=h(x)+c(x,y))
The h value of Y is not adjusted, but y is added to the open table:
1,k_old!=h(x) &&(b(Y)!= X and h(Y)>h(x)+c(x,y) && t(Y)= "closed" and h(Y)>K_old
py code
insert(x,h)
def insert(state, h_new): if state.t == "new": state.k = h_new elif state.t == "open": state.k = min(state.k, h_new) elif state.t == "closed": state.k = min(state.k, h_new) state.h = h_new state.t = "open" open_list.add(state)
min_state()
def min_state():
if not open_list:
print("Open_list is NULL")
return None
return min(open_list, key=lambda x: x.k) # Get the node corresponding to the smallest k value in openlist
get_kmin()
def get_kmin():
if not open_list:
return -1
return min([x.k for x in open_list]) # Get the k with the smallest value in the openlist table
cos(x,y)
def cost(X, Y): if X.state == "#" or Y.state == "#": return maxsize return X.cost(Y)
process_state()
def process_state():
x = min_state()
if x is None:
return -1
old_k = get_kmin()
delete(x)
if old_k < x.h:
for y in map.get_neighbors(x):
if y.h<=old_k and x.h > y.h + cost(x,y):
x.parent = y
x.h = y.h + x.cost(y)
if old_k == x.h:
for y in self.map.get_neighbors(x):
if ( (y.t == "new" or \
y.parent == x and y.h != x.h + cost(x,y) or\
y.parent != x and y.h > x.h + cost(x,y)) )and\
y != end:
y.parent = x
insert(y, x.h + cost(x,y))
else:
for y in self.map.get_neighbors(x):
if y.t == "new" or \
y.parent == x and y.h != x.h + cost(x,y):
y.parent = x
insert(y, x.h + cost(x,y))
else:
if y.parent != x and y.h > x.h + cost(x,y):
insert(x, x.h)
else:
if y.parent != x and x.h > y.h + cost(x,y) and \
y.t == "closed" and y.h > old_k:
insert(y, y.h)
return get_kmin()
modify_cost(X, Y,cval)
def modify_cost(X, Y,cval):
X.cost(Y)=cval
if X.t == "closed":
insert(X, X.h)
D * algorithm
def D_star(start, end):
open_list.add(end)
/'reverse Dijkstra'/
while True:
process_state()
if start.t == "close":
break
/'Find path'/
s = start
while s != end:
s = s.parent
tmp = start # The starting point remains unchanged
map.set_obstacle([(9, 3), (9, 4), (9, 5), (9, 6), (9, 7), (9, 8)]) # lay down a screen
/'Add to openlist And re planning'/
while tmp != end:
if tmp.parent.state == "#":
modify_cost(tmp)
while True:
k_min = process_state()
if k_min >= tmp.h:
break
continue
tmp = tmp.parent
reference material: D * algorithm
(86 messages) d * algorithm (Dynamic A Star)_ Demon rice blog - CSDN blog_ D * algorithm