1, Title [LeetCode-21]

Merge the two ascending linked lists into a new} ascending linked list and return. The new linked list is composed of all nodes of a given two linked lists.  

Example 1:

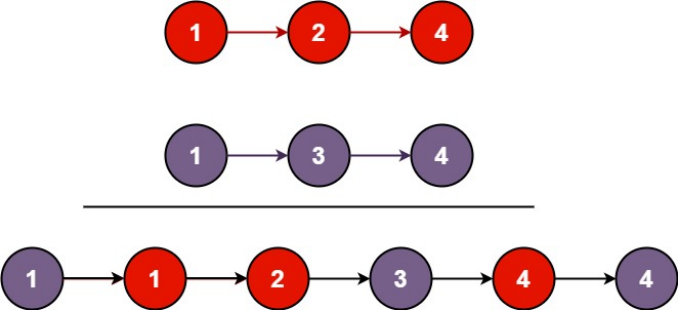
Input: l1 = [1,2,4], l2 = [1,3,4]

Output: [1,1,2,3,4,4]

Example 2:

Input: l1 = [], l2 = []

Output: []

Example 3:

Input: l1 = [], l2 = [0]

Output: [0]

Tips:

• The node number range of the two linked lists is [0, 50]
• -100 <= Node.val <= 100
• l1 and l2 are arranged in non decreasing order

2, Train of thought

iteration

For the merging of two lists, you can ① create a new table to store the merged List, or ② for the two tables, select the smaller first element as the main chain and the other as the attached chain, and then traverse the two tables with i pointer and j pointer respectively, Judge whether the value of J is between [i, i+1] (J - > val ≥ i - > Val must be satisfied, just judge whether J - > Val < i - > next - > VAL). If yes, insert J between [i, i+1] (create a new ListNode, copy J - > Val as the value) and update J; Otherwise, i will be updated backward.

The idea ② is used here. As mentioned above, to exit the loop, either j has traversed to the end or i has traversed to the end. If it is the former, it can directly return to the first element node of i; If it is the latter and j has not been traversed, connect j and all subsequent elements to i, and finally return to the first element node of i.

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if(list1 == nullptr)
            return list2;
        if(list2 == nullptr)
            return list1;//Handle degradation of empty lists
        if(list1->val > list2->val)
            return mergeTwoLists(list2, list1);//For two tables, select the smaller first element as the main chain and the other as the attached chain
        ListNode* i = list1;
        ListNode* j = list2;
        while(i->next != nullptr&&j != nullptr)
        {
            if(i->next->val > j->val)//If the value of the chain attached pointer j is less than the value of the next bit of the main chain pointer i, that is, the value of j is between the values of [i, i+1]
            {
                i->next = new ListNode(j->val, i->next);//Then insert j (copy value) between i and i+1 on the main chain
                j = j->next;//Original J is inserted and j is updated
            }
            else//If the value of the chain attached pointer j is greater than or equal to the value of the next bit of the main chain pointer i, that is, the value of j is after the value of [i, i+1]
                i = i->next;//Then I will be updated, and the next cycle will let j compare with [i+1, i+2] before I update whether its value is in the middle
        }//After the loop is completed or the value of the attached chain has been inserted, the pointer of the first node of the main chain can be returned directly;
        while(j)//Either the value of the attached chain has not been inserted and is greater than the value of the end node of the main chain
        {
            i->next = new ListNode(j->val, j->next);
            i = i->next;
            j = j->next;
        }
        return list1;
    }
};

 

3, Official solution (source: LeetCode)

Method 1: recursion

We can recursively define merge operations in two linked lists as follows (ignoring boundary conditions, such as empty linked lists):

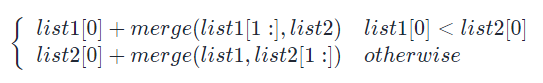
That is, the node with the smaller header value of the two linked lists is merged with the merge operation results of the remaining elements.

We directly model the above recursive process, and we need to consider the boundary.

If l1 or l2 is an empty linked list at the beginning, there is no operation to merge, so we only need to return a non empty linked list. Otherwise, we need to determine which of l1 and l2 has a smaller value, and then recursively determine the next node to be added to the result. If one of the two linked lists is empty, the recursion ends.

 

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        if (l1 == nullptr) {
            return l2;
        } else if (l2 == nullptr) {
            return l1;
        } else if (l1->val < l2->val) {
            l1->next = mergeTwoLists(l1->next, l2);
            return l1;
        } else {
            l2->next = mergeTwoLists(l1, l2->next);
            return l2;
        }
    }
};

Author: LeetCode-Solution
 Link: https://leetcode-cn.com/problems/merge-two-sorted-lists/solution/he-bing-liang-ge-you-xu-lian-biao-by-leetcode-solu/
Source: force buckle( LeetCode)
The copyright belongs to the author. For commercial reprint, please contact the author for authorization, and for non-commercial reprint, please indicate the source.

Complexity analysis

• Time complexity: O(n+m), where N and m are the lengths of the two linked lists respectively. Because each recursive call will remove the head node of l1 or l2 (until at least one linked list is empty), the function mergeTwoList will only call each node recursively at most once. Therefore, the time complexity depends on the length of the combined linked list, i.e. O(n+m)O(n+m).
• Spatial complexity: O(n+m), where N and m are the lengths of the two linked lists respectively. When calling the mergeTwoLists function recursively, the stack space needs to be consumed. The size of the stack space depends on the depth of the recursive call. At the end of the recursive call, the mergeTwoLists function can be called at most n+m times, so the space complexity is O(n+m).

Method 2: iteration

We can use iterative method to implement the above algorithm. When neither l1 nor l2 is an empty linked list, judge which of l1 and l2 has the smaller value of the head node, and add the node with the smaller value to the result. When a node is added to the result, move the node in the corresponding linked list back one bit.

First, we ① set a sentinel node prehead, which makes it easier for us to return to the merged linked list at the end. We ② maintain a prev pointer. What we need to do is adjust its next pointer. Then, we repeat the following process until l1 or l2 points to null: if the value of the current l1 node is less than or equal to l2, we connect the current l1 node to the prev node and move the l1 pointer back one bit. Otherwise, we do the same for l2. No matter which element we follow, we need to move prev back one bit.

At most one of l1 and l2 is non empty at the end of the loop. Because the two input linked lists are ordered, no matter which linked list is non empty, all the elements contained in it are larger than all the elements in the merged linked list. This means that we simply connect the non empty linked list to the merged linked list and return to the merged linked list.

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode* preHead = new ListNode(-1);

        ListNode* prev = preHead;
        while (l1 != nullptr && l2 != nullptr) {
            if (l1->val < l2->val) {
                prev->next = l1;
                l1 = l1->next;
            } else {
                prev->next = l2;
                l2 = l2->next;
            }
            prev = prev->next;
        }

        // After merging, at most one l1 and l2 has not been merged. We can directly point the end of the linked list to the unfinished linked list
        prev->next = l1 == nullptr ? l2 : l1;

        return preHead->next;
    }
};

Author: LeetCode-Solution
 Link: https://leetcode-cn.com/problems/merge-two-sorted-lists/solution/he-bing-liang-ge-you-xu-lian-biao-by-leetcode-solu/
Source: force buckle( LeetCode)
The copyright belongs to the author. For commercial reprint, please contact the author for authorization, and for non-commercial reprint, please indicate the source.

Complexity analysis

• Time complexity: O(n+m), where N and m are the lengths of the two linked lists respectively. Because only one element of l1 and l2 will be put into the combined linked list in each loop iteration, the number of while loops will not exceed the sum of the lengths of the two linked lists. The time complexity of all other operations is constant, so the total time complexity is O(n+m).
• Space complexity: O(1). We only need constant space to store several variables.

4, Learning experience

① The magic of recursion. The recursive method in the official solution of this problem is particularly ingenious. After finding out the recursive formula, a few lines of code solve a big problem.

② The setting of the head sentry element. The iterative method of the official solution is the idea ①. If you directly synthesize the two linked lists into a new linked list, you will have no way to start, because it is difficult to determine the next relationship between the new linked list nodes after comparing the sizes of pointers i and j. Here, you can set the head sentinel node prehead, and the first element is the subsequent prehead - > next. Then, you can adjust the next relationship between subsequent nodes by maintaining the "current" pointer prev. Finally, return to prehead - > next.